Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

PROBLEMS

237

4.1 and 4.2 Knowing that the couple shown acts in a vertical plane,

determine the stress at (a) point A, (b) point B.

2 in.

1.5 in.

2 in.

2 in.2 in.

M  25 kip · in.

Fig. P4.1

M  15 kN · m

Dimensions in mm

20 40 20

Fig. P4.2

4.3 Using an allowable stress of 16 ksi, determine the largest couple

that can be applied to each pipe.

4.4 A nylon spacing bar has the cross section shown. Knowing that the

allowable stress for the grade of nylon used is 24 MPa, determine

the largest couple M

that can be applied to the bar.

0.1 in.

0.2 in.

0.5 in.

(a)

(b)

Fig. P4.3

100 mm

80 mm

r  25 mm

Fig. P4.4

4.5 A beam of the cross section shown is extruded from an aluminum

alloy for which s

5 250 MPa and s

5 450 MPa. Using a factor

of safety of 3.00, determine the largest couple that can be applied

to the beam when it is bent about the z axis.

24 mm

80 mm

24 mm

16 mm

Fig. P4.5

4.6 Solve Prob. 4.5, assuming that the beam is bent about the y axis.

bee80288_ch04_220-313.indd Page 237 10/26/10 4:26:21 PM user-f499bee80288_ch04_220-313.indd Page 237 10/26/10 4:26:21 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

238

Pure Bending

4.7 and 4.8 Two W4 3 13 rolled sections are welded together as

shown. Knowing that for the steel alloy used, s

5 36 ksi and s

58 ksi and using a factor of safety of 3.0, determine the largest couple

that can be applied when the assembly is bent about the z axis.

Fig. P4.7

Fig. P4.8

4.9 through 4.11 Two vertical forces are applied to a beam of the

cross section shown. Determine the maximum tensile and com-

pressive stresses in portion BC of the beam.

300 mm 300 mm

25 mm

4 kN4 kN

Fig. P4.9

DCBA

25 kips 25 kips

20 in. 20 in.

60 in.

4 in.

1 in.

6 in.

8 in.

Fig. P4.11

10 mm 10 mm

50 mm

10 mm

150 mm 150 mm

10 kN 10 kN

250 mm

50 mm

Fig. P4.10

4.12 Knowing that a beam of the cross section shown is bent about a

horizontal axis and that the bending moment is 6 kN ? m, deter-

mine the total force acting on the top flange.

4.13 Knowing that a beam of the cross section shown is bent about a

horizontal axis and that the bending moment is 6 kN ? m, deter-

mine the total force acting on the shaded portion of the web.

72 mm

216 mm

36 mm

54 mm

108 mm

Fig. P4.12 and P4.13

bee80288_ch04_220-313.indd Page 238 10/26/10 4:26:43 PM user-f499bee80288_ch04_220-313.indd Page 238 10/26/10 4:26:43 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

239

Problems

4.14 Knowing that a beam of the cross section shown is bent about a

horizontal axis and that the bending moment is 50 kip ? in., deter-

mine the total force acting (a) on the top flange (b) on the shaded

portion of the web.

4.15 The beam shown is made of a nylon for which the allowable stress

is 24 MPa in tension and 30 MPa in compression. Determine the

largest couple M that can be applied to the beam.

1.5 in.

4 in.

2 in.

6 in.

Fig. P4.14

15 mm

d  30 mm

20 mm

40 mm

Fig. P4.15

4.16 Solve Prob. 4.15, assuming that d 5 40 mm.

4.17 Knowing that for the extruded beam shown the allowable stress is

12 ksi in tension and 16 ksi in compression, determine the largest

couple M that can be applied.

4.18 Knowing that for the casting shown the allowable stress is 5 ksi in

tension and 18 ksi in compression, determine the largest couple M

that can be applied.

1.5 in.

0.5 in.

1.5 in.

0.5 in. 0.5 in.

0.5 in.

Fig. P4.17

0.5 in.

1 in.

Fig. P4.18

4.19 and 4.20 Knowing that for the extruded beam shown the

allowable stress is 120 MPa in tension and 150 MPa in compres-

sion, determine the largest couple M that can be applied.

50 mm

125 mm

150 mm

Fig. P4.19

54 mm

40 mm

80 mm

Fig. P4.20

bee80288_ch04_220-313.indd Page 239 10/26/10 4:26:57 PM user-f499bee80288_ch04_220-313.indd Page 239 10/26/10 4:26:57 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

240

Pure Bending

4.21 A steel band saw blade, that was originally straight, passes over

8-in.-diameter pulleys when mounted on a band saw. Determine

the maximum stress in the blade, knowing that it is 0.018 in. thick

and 0.625 in. wide. Use E 5 29 3 10

psi.

4.22 Straight rods of 0.30-in. diameter and 200-ft length are sometimes

used to clear underground conduits of obstructions or to thread

wires through a new conduit. The rods are made of high-strength

steel and, for storage and transportation, are wrapped on spools of

5-ft diameter. Assuming that the yield strength is not exceeded,

determine (a) the maximum stress in a rod, when the rod, which

is initially straight, is wrapped on a spool, (b) the corresponding

bending moment in the rod. Use E 5 29 3 10

psi.

0.018 in.

Fig. P4.21

4.23 A 900-mm strip of steel is bent into a full circle by two couples

applied as shown. Determine (a) the maximum thickness t of the

strip if the allowable stress of the steel is 420 MPa, (b) the corre-

sponding moment M of the couples. Use E 5 200 GPa.

4.24 A 60-N ? m couple is applied to the steel bar shown. (a) Assuming

that the couple is applied about the z axis as shown, determine the

maximum stress and the radius of curvature of the bar. (b) Solve

part a, assuming that the couple is applied about the y axis. Use

E 5 200 GPa.

5 ft

Fig. P4.22

900 mm

8 mm

MM'

Fig. P4.23

20 mm

12 mm

60 N · m

Fig. P4.24

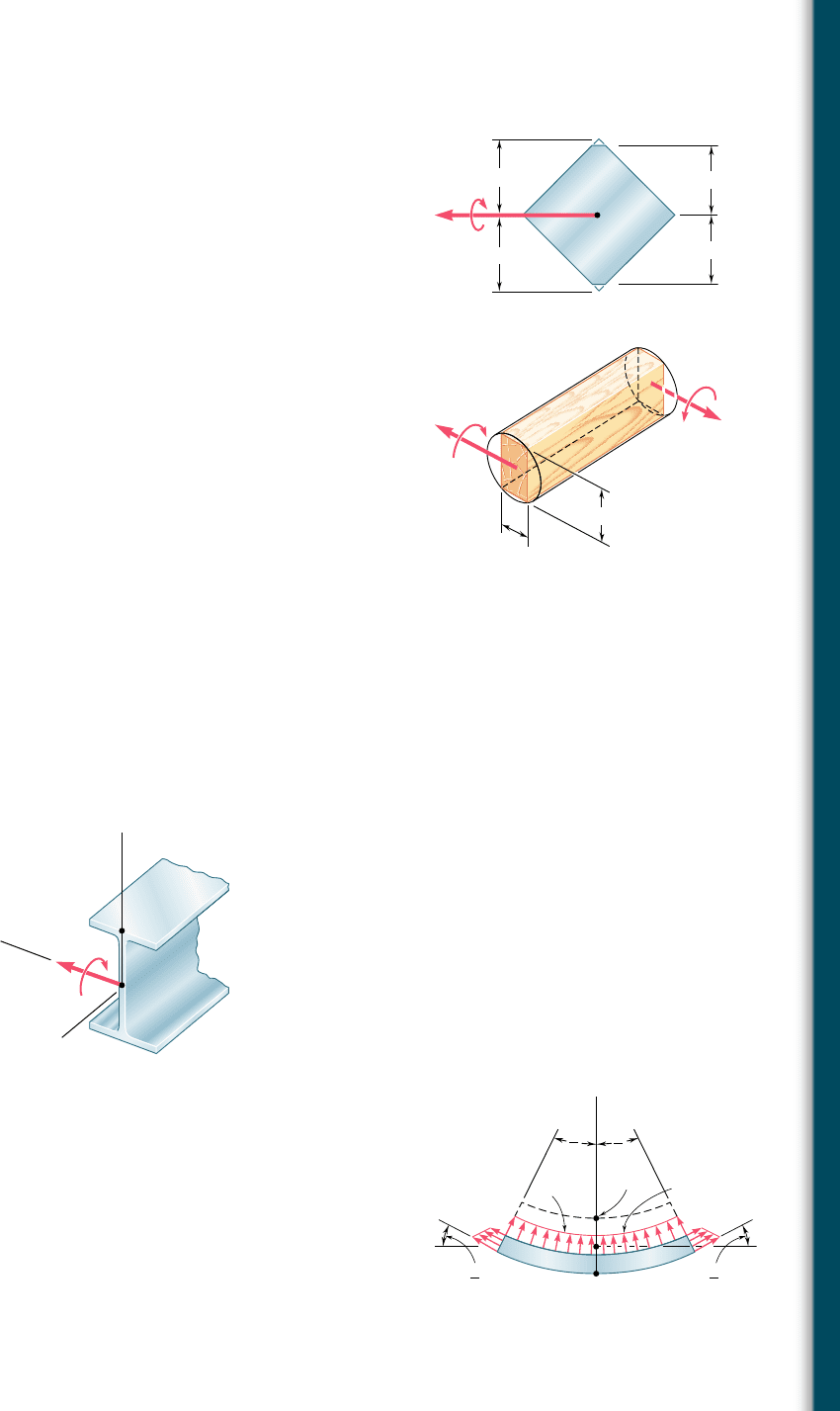
4.25 A couple of magnitude M is applied to a square bar of side a. For

each of the orientations shown, determine the maximum stress and

the curvature of the bar.

(a)

(b)

Fig. P4.25

bee80288_ch04_220-313.indd Page 240 11/11/10 3:03:11 PM user-f499bee80288_ch04_220-313.indd Page 240 11/11/10 3:03:11 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

241

Problems

4.26 A portion of a square bar is removed by milling, so that its cross

section is as shown. The bar is then bent about its horizontal axis

by a couple M. Considering the case where h 5 0.9h

, express

the maximum stress in the bar in the form s

5 ks

where s

is the maximum stress that would have occurred if the original

square bar had been bent by the same couple M, and determine

the value of k.

4.27 In Prob. 4.26, determine (a) the value of h for which the maximum

stress s

is as small as possible, (b) the corresponding value of k.

4.28 A couple M will be applied to a beam of rectangular cross section

that is to be sawed from a log of circular cross section. Determine

the ratio dyb for which (a) the maximum stress s

will be as small

as possible, (b) the radius of curvature of the beam will be

maximum.

4.29 For the aluminum bar and loading of Sample Prob. 4.1, determine

(a) the radius of curvature r9 of a transverse cross section, (b) the

angle between the sides of the bar that were originally vertical. Use

E 5 10.6 3 10

psi and n 5 0.33.

4.30 For the bar and loading of Example 4.01, determine (a) the radius

of curvature r, (b) the radius of curvature r9 of a transverse cross

section, (c) the angle between the sides of the bar that were origi-

nally vertical. Use E 5 29 3 10

psi and n 5 0.29.

4.31 A W200 3 31.3 rolled-steel beam is subjected to a couple M of

moment 45 kN ? m. Knowing that E 5 200 GPa and n 5 0.29,

determine (a) the radius of curvature r, (b) the radius of curvature

r9 of a transverse cross section.

Fig. P4.26

Fig. P4.28

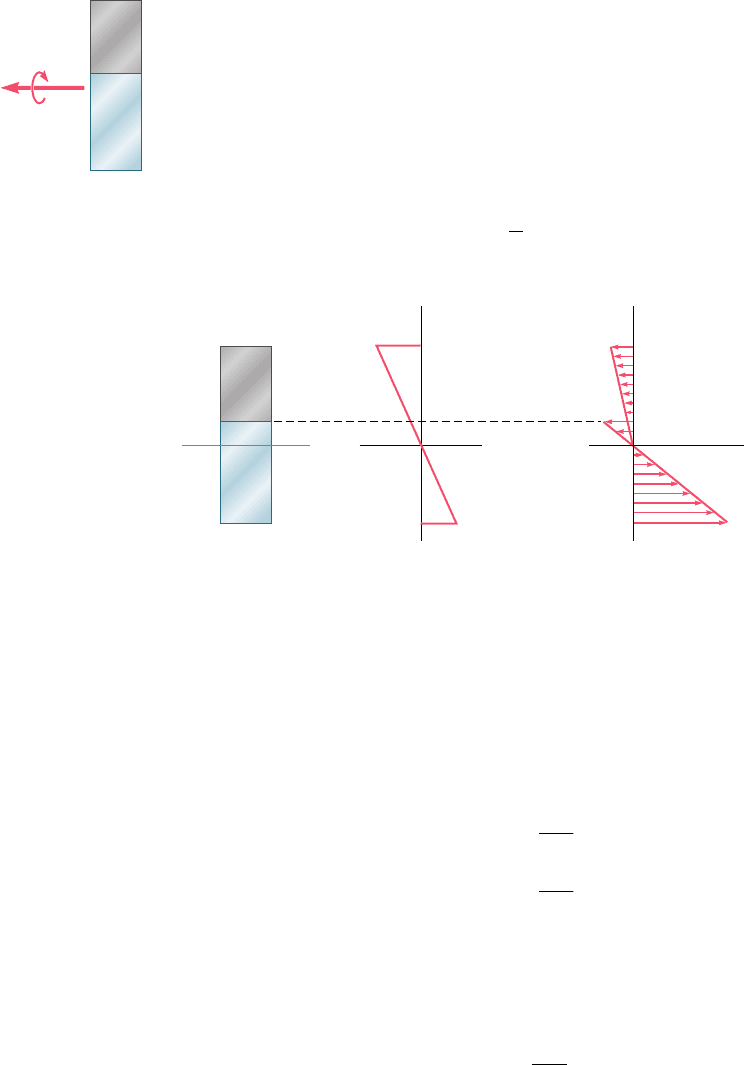
4.32 It was assumed in Sec. 4.3 that the normal stresses s

in a member

in pure bending are negligible. For an initially straight elastic

member of rectangular cross section, (a) derive an approximate

expression for s

as a function of y, (b) show that (s

)

max

2(cy2r)(s

)

max

and, thus, that s

can be neglected in all practical

situations. (Hint: Consider the free-body diagram of the portion of

beam located below the surface of ordinate y and assume that the

distribution of the stress s

is still linear.)

Fig. P4.31





y  c

y  c



Fig. P4.32

bee80288_ch04_220-313.indd Page 241 10/26/10 4:27:21 PM user-f499bee80288_ch04_220-313.indd Page 241 10/26/10 4:27:21 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

242

Pure Bending

4.6 BENDING OF MEMBERS MADE OF

SEVERAL MATERIALS

The derivations given in Sec. 4.4 were based on the assumption of

a homogeneous material with a given modulus of elasticity E. If the

member subjected to pure bending is made of two or more materials

with different moduli of elasticity, our approach to the determination

of the stresses in the member must be modified.

Consider, for instance, a bar consisting of two portions of differ-

ent materials bonded together as shown in cross section in Fig. 4.20.

This composite bar will deform as described in Sec. 4.3, since its cross

section remains the same throughout its entire length, and since no

assumption was made in Sec. 4.3 regarding the stress-strain relation-

ship of the material or materials involved. Thus, the normal strain P

still varies linearly with the distance y from the neutral axis of the

section (Fig. 4.21a and b), and formula (4.8) holds:

(4.8)

Fig. 4.20 Cross

section with two

materials.

N. A.

⫽

– —

⑀

␴

␳

⫽

– —–

␴

␳

⫽

– —–

␴

␳

(a)(b)(c)

Fig. 4.21 Strain and stress distribution in bar made of two materials.

However, we cannot assume that the neutral axis passes through the

centroid of the composite section, and one of the goals of the present

analysis will be to determine the location of this axis.

Since the moduli of elasticity E

and E

of the two materials

are different, the expressions obtained for the normal stress in each

material will also be different. We write

5 E

(4.24)

and obtain a stress-distribution curve consisting of two segments of

straight line (Fig. 4.21c). It follows from Eqs. (4.24) that the force

exerted on an element of area dA of the upper portion of the

cross section is

5 s

dA 52

dA (4.25)

bee80288_ch04_220-313.indd Page 242 10/28/10 9:25:32 PM user-f499bee80288_ch04_220-313.indd Page 242 10/28/10 9:25:32 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

243

while the force dF

exerted on an element of the same area dA of the

lower portion is

5 s

dA 52

dA (4.26)

But, denoting by n the ratio E

of the two moduli of elasticity, we can

express dF

1nE

dA 52

1n dA2 (4.27)

Comparing Eqs. (4.25) and (4.27), we note that the same force dF

would be exerted on an element of area n dA of the first material. In

other words, the resistance to bending of the bar would remain the

same if both portions were made of the first material, provided that

the width of each element of the lower portion were multiplied by the

factor n. Note that this widening (if n . 1), or narrowing (if n , 1),

must be effected in a direction parallel to the neutral axis of the sec-

tion, since it is essential that the distance y of each element from the

neutral axis remain the same. The new cross section obtained in this

way is called the transformed section of the member (Fig. 4.22).

Since the transformed section represents the cross section of a

member made of a homogeneous material with a modulus of elastic-

ity E

, the method described in Sec. 4.4 can be used to determine

the neutral axis of the section and the normal stress at various points

of the section. The neutral axis will be drawn through the centroid

of the transformed section (Fig. 4.23), and the stress s

at any point

of the corresponding fictitious homogeneous member will be obtained

from Eq. (4.16)

(4.16)

where y is the distance from the neutral surface, and I the moment of

inertia of the transformed section with respect to its centroidal axis.

To obtain the stress s

at a point located in the upper portion of

the cross section of the original composite bar, we simply compute the

stress s

at the corresponding point of the transformed section. However,

to obtain the stress s

at a point in the lower portion of the cross section,

we must multiply by n the stress s

computed at the corresponding point

of the transformed section. Indeed, as we saw earlier, the same elemen-

tary force dF

is applied to an element of area n dA of the transformed

section and to an element of area dA of the original section. Thus, the

stress s

at a point of the original section must be n times larger than

the stress at the corresponding point of the transformed section.

The deformations of a composite member can also be deter-

mined by using the transformed section. We recall that the trans-

formed section represents the cross section of a member, made of a

homogeneous material of modulus E

, which deforms in the same

manner as the composite member. Therefore, using Eq. (4.21), we

write that the curvature of the composite member is

where I is the moment of inertia of the transformed section with

respect to its neutral axis.

4.6 Bending of Members Made

of Several Materials

dA ndA

nbb

Fig. 4.22 Transformed section for

composite bar.

N. A.



– —–



Fig. 4.23 Distribution of stresses in

transformed section.

bee80288_ch04_220-313.indd Page 243 10/27/10 5:46:14 PM user-f499bee80288_ch04_220-313.indd Page 243 10/27/10 5:46:14 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

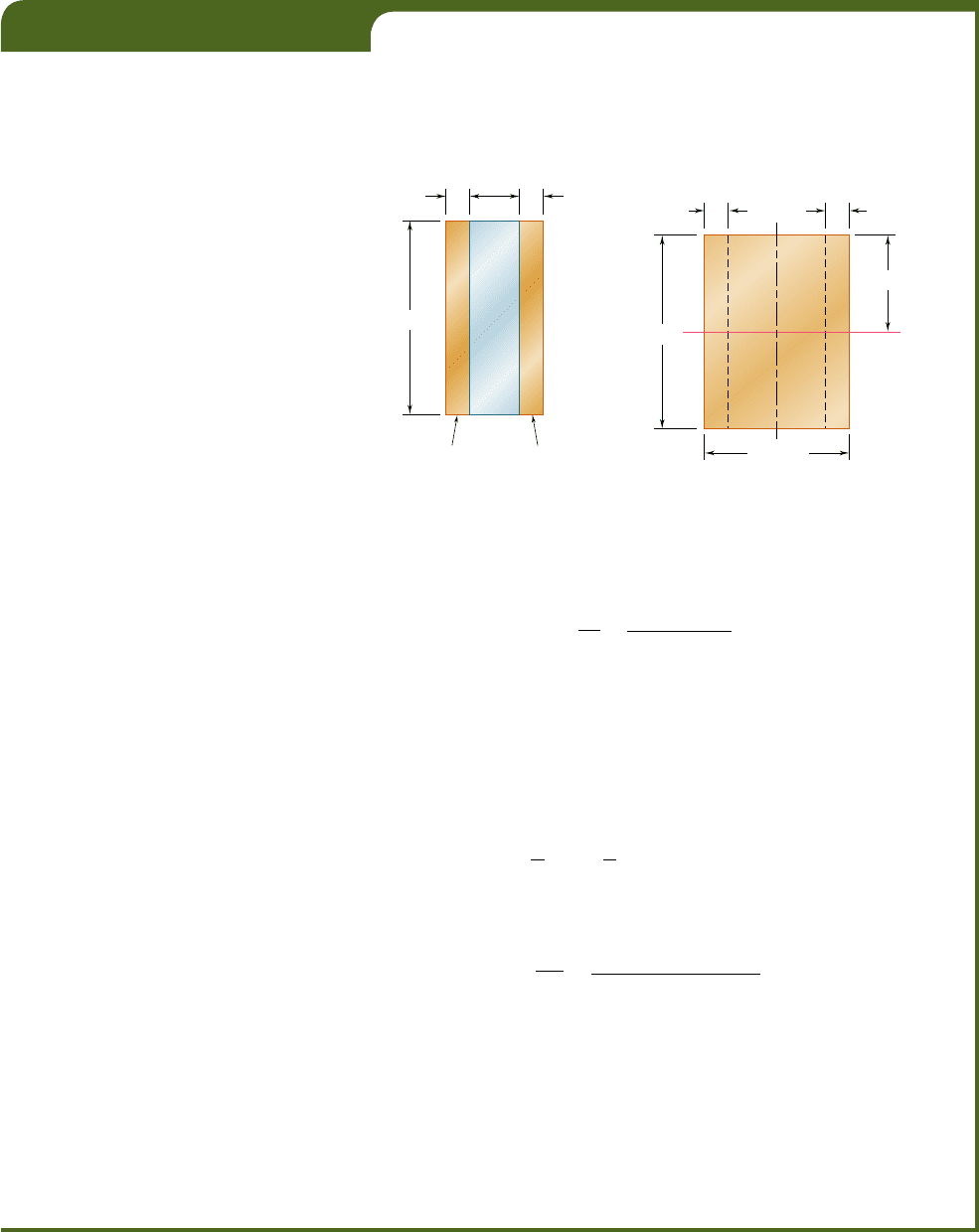
Apago PDF Enhancer

244

A bar obtained by bonding together pieces of steel (E

5 29 3 10

psi) and

brass (E

5 15 3 10

psi) has the cross section shown (Fig. 4.24). Deter-

mine the maximum stress in the steel and in the brass when the bar is in

pure bending with a bending moment M 5 40 kip ? in.

EXAMPLE 4.03

1.45 in.

2.25 in.

0.4 in. 0.4 in.

3 in.

c  1.5 in.

All brass

N. A.

Fig. 4.25

0.75 in.

0.4 in. 0.4 in.

3 in.

Steel

Brass Brass

Fig. 4.24

The transformed section corresponding to an equivalent bar made

entirely of brass is shown in Fig. 4.25. Since

n 5

29 3 10

psi

15 3 10

psi

5 1.933

the width of the central portion of brass, which replaces the original steel

portion, is obtained by multiplying the original width by 1.933, we have

(0.75 in.)(1.933) 5 1.45 in.

Note that this change in dimension occurs in a direction parallel to the

neutral axis. The moment of inertia of the transformed section about its

centroidal axis is

I 5

12.25 in.213 in.2

5 5.063 in

and the maximum distance from the neutral axis is c 5 1.5 in. Using

Eq. (4.15), we find the maximum stress in the transformed section:

140 kip ? in.211.5 in.

063 in

5 11.85 ksi

The value obtained also represents the maximum stress in the brass por-

tion of the original composite bar. The maximum stress in the steel por-

tion, however, will be larger than the value obtained for the transformed

section, since the area of the central portion must be reduced by the

factor n 5 1.933 when we return from the transformed section to the

original one. We thus conclude that

brass

max

5 11.85 ksi

steel

max

5 11.9332111.85 ksi25 22.9 ksi

bee80288_ch04_220-313.indd Page 244 10/26/10 4:27:39 PM user-f499bee80288_ch04_220-313.indd Page 244 10/26/10 4:27:39 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

245

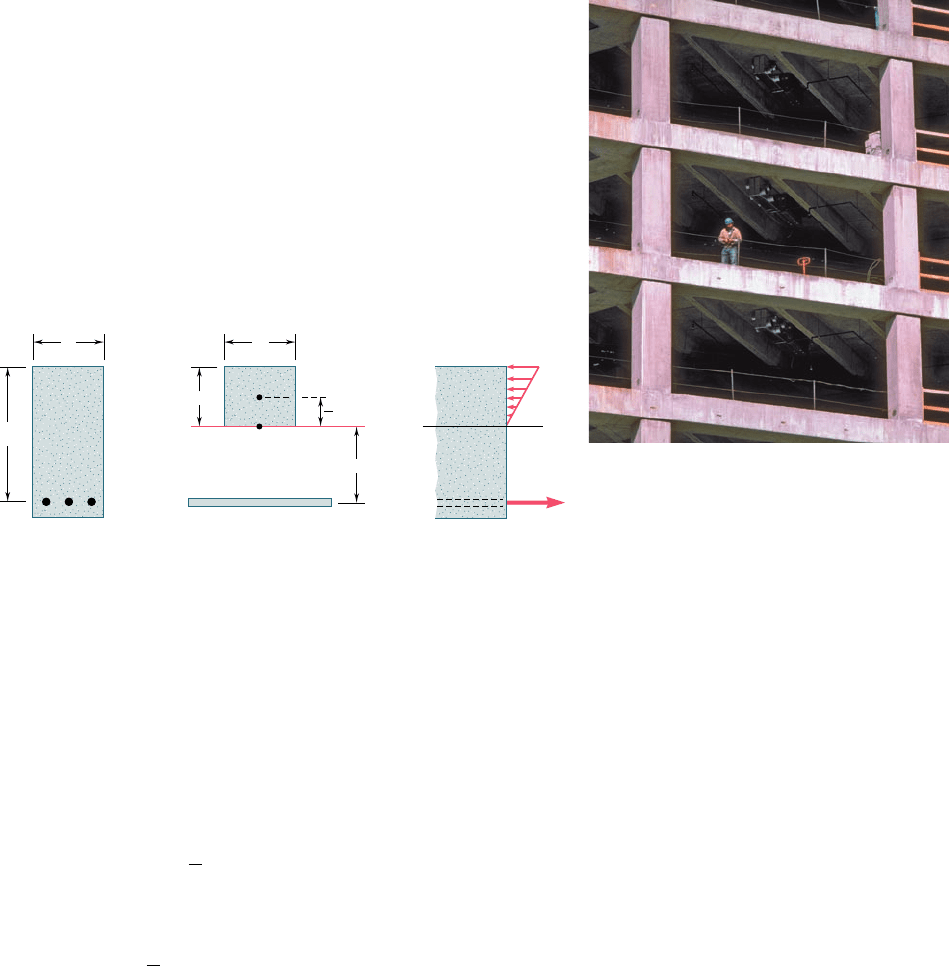
An important example of structural members made of two dif-

ferent materials is furnished by reinforced concrete beams (Photo

4.4). These beams, when subjected to positive bending moments, are

reinforced by steel rods placed a short distance above their lower

face (Fig. 4.26a). Since concrete is very weak in tension, it will crack

below the neutral surface and the steel rods will carry the entire

tensile load, while the upper part of the concrete beam will carry

the compressive load.

To obtain the transformed section of a reinforced concrete

beam, we replace the total cross-sectional area A

of the steel bars

by an equivalent area nA

, where n is the ratio E

of the moduli

of elasticity of steel and concrete (Fig. 4.26b). On the other hand,

since the concrete in the beam acts effectively only in compression,

only the portion of the cross section located above the neutral axis

should be used in the transformed section.

Photo 4.4 Reinforced concrete building.

N. A.

d – x



(a)(b)(c)

Fig. 4.26 Reinforced concrete beam.

The position of the neutral axis is obtained by determining the

distance x from the upper face of the beam to the centroid C of the

transformed section. Denoting by b the width of the beam, and by

d the distance from the upper face to the center line of the steel

rods, we write that the first moment of the transformed section with

respect to the neutral axis must be zero. Since the first moment of

each of the two portions of the transformed section is obtained by

multiplying its area by the distance of its own centroid from the

neutral axis, we have

1bx2

2 nA

1d 2 x25 0

1 nA

x 2 nA

d 5 0 (4.28)

Solving this quadratic equation for x, we obtain both the position of

the neutral axis in the beam, and the portion of the cross section of

the concrete beam that is effectively used.

The determination of the stresses in the transformed section is

carried out as explained earlier in this section (see Sample Prob. 4.4).

The distribution of the compressive stresses in the concrete and

the resultant F

of the tensile forces in the steel rods are shown in

Fig. 4.26c.

4.6 Bending of Members Made

of Several Materials

bee80288_ch04_220-313.indd Page 245 10/27/10 5:46:14 PM user-f499bee80288_ch04_220-313.indd Page 245 10/27/10 5:46:14 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

246

Pure Bending

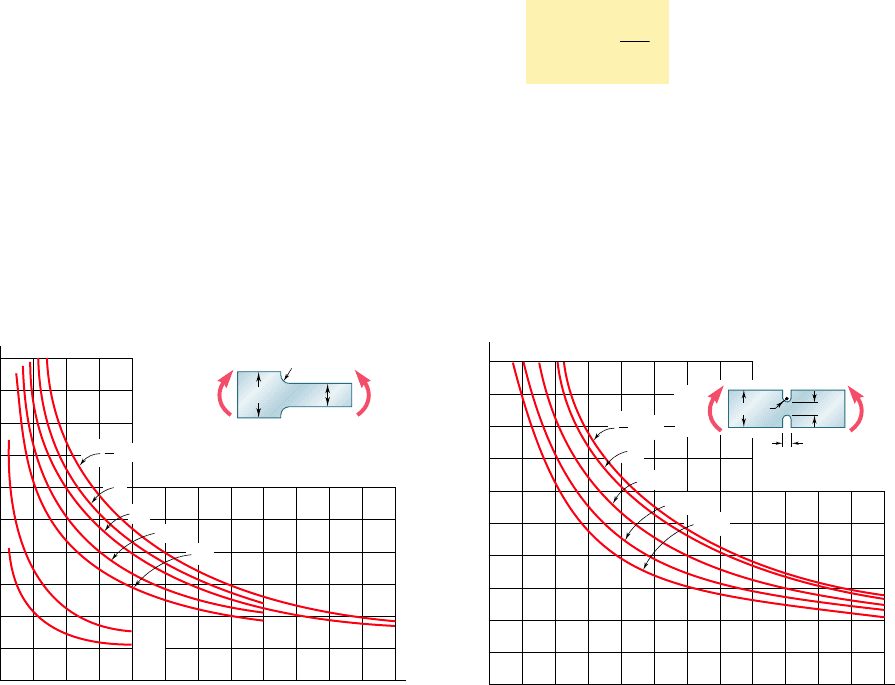
4.7 STRESS CONCENTRATIONS

The formula s

5 McyI was derived in Sec. 4.4 for a member with a

plane of symmetry and a uniform cross section, and we saw in Sec. 4.5

that it was accurate throughout the entire length of the member only

if the couples M and M9 were applied through the use of rigid and

smooth plates. Under other conditions of application of the loads, stress

concentrations will exist near the points where the loads are applied.

Higher stresses will also occur if the cross section of the mem-

ber undergoes a sudden change. Two particular cases of interest have

been studied,† the case of a flat bar with a sudden change in width,

and the case of a flat bar with grooves. Since the distribution of

stresses in the critical cross sections depends only upon the geometry

of the members, stress-concentration factors can be determined for

various ratios of the parameters involved and recorded as shown in

Figs. 4.27 and 4.28. The value of the maximum stress in the critical

cross section can then be expressed as

5 K

(4.29)

where K is the stress-concentration factor, and where c and I refer to

the critical section, i.e., to the section of width d in both of the cases

considered here. An examination of Figs. 4.27 and 4.28 clearly shows the

importance of using fillets and grooves of radius r as large as practical.

Finally, we should point out that, as was the case for axial load-

ing and torsion, the values of the factors K have been computed under

the assumption of a linear relation between stress and strain. In many

applications, plastic deformations will occur and result in values of

the maximum stress lower than those indicated by Eq. (4.29).

3.0

2.8

2.6

2.4

2.2

2.0

1.8

1.6

1.4

1.2

1.0

0 0.05 0.10 0.15 0.20 0.25 0.3

r/d

 3

1.5

1.2

1.1

1.02

1.01

MM'

Fig. 4.27 Stress-concentration factors for flat bars with

fillets under pure bending.†

3.0

2.8

2.6

2.4

2.2

2.0

1.8

1.6

1.4

1.2

1.0

0 0.05 0.10 0.15 0.20 0.25 0.30

r/d

 2

1.5

1.2

1.1

1.05

Fig. 4.28 Stress-concentration factors for flat bars with

grooves under pure bending.†

†W. D. Pilkey, Peterson’s Stress Concentration Factors, 2d ed., John Wiley & Sons, New

York, 1997.

bee80288_ch04_220-313.indd Page 246 10/26/10 4:27:50 PM user-f499bee80288_ch04_220-313.indd Page 246 10/26/10 4:27:50 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles