Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

217

Review Problems

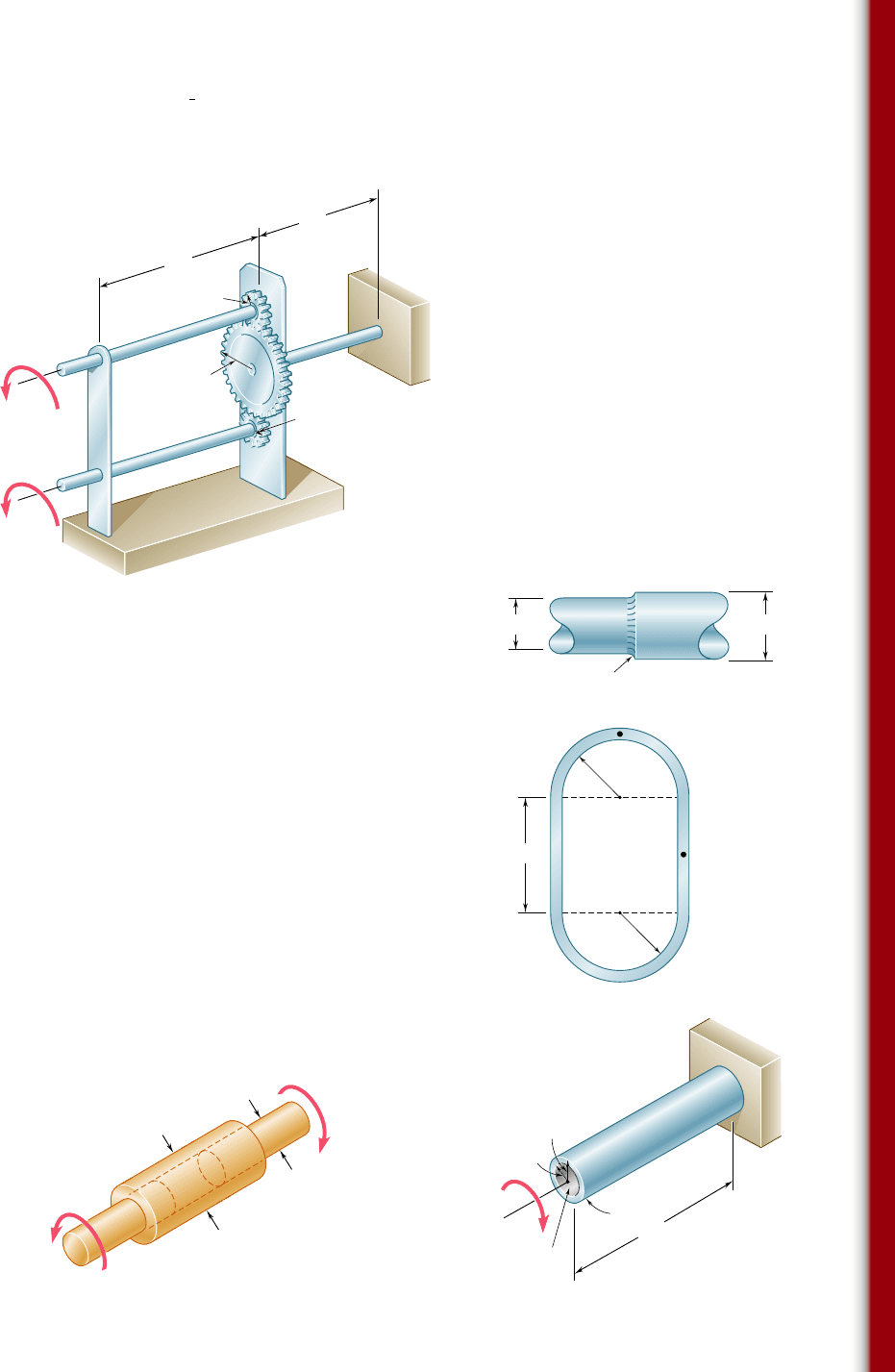
3.157 Three solid shafts, each of

-in. diameter, are connected by the

gears as shown. Knowing that G 5 11.2 3 10

psi, determine (a) the

angle through which end A of shaft AB rotates, (b) the angle

through which end E of shaft EF rotates.

4 in.

6 in.

2 in.

3 ft

4 ft

r  1.5 in.

⫽ 100 lb · in.

⫽ 200 lb · in.

Fig. P3.157

3.158 The design specifications of a 1.2-m-long solid transmission shaft

require that the angle of twist of the shaft not exceed 48 when a torque

of 750 N ? m is applied. Determine the required diameter of the shaft,

knowing that the shaft is made of a steel with an allowable shearing

stress of 90 MPa and a modulus of rigidity of 77.2 GPa.

3.159 The stepped shaft shown rotates at 450 rpm. Knowing that r 5

0.5 in., determine the maximum power that can be transmitted

without exceeding an allowable shearing stress of 7500 psi.

3.160 A 750-N ? m torque is applied to a hollow shaft having the cross

section shown and a uniform 6-mm wall thickness. Neglecting the

effect of stress concentrations, determine the shearing stress at

points a and b.

3.161 The composite shaft shown is twisted by applying a torque T at end

A. Knowing that the maximum shearing stress in the steel shell is

150 MPa, determine the corresponding maximum shearing stress in

the aluminum core. Use G 5 77.2 GPa for steel and G 5 27 GPa

for aluminum.

3.162 Two solid brass rods AB and CD are brazed to a brass sleeve EF.

Determine the ratio d

for which the same maximum shearing

stress occurs in the rods and in the sleeve.

6 in.5 in.

Fig. P3.159

30 mm

60 mm

30 mm

Fig. P3.160

2 m

30 mm

40 mm

Steel

Aluminum

Fig. P3.161

Fig. P3.162

bee80288_ch03_140-219.indd Page 217 9/21/10 9:21:14 PM user-f499bee80288_ch03_140-219.indd Page 217 9/21/10 9:21:14 PM user-f499 /Users/user-f499/Desktop/Users/user-f499/Desktop

Apago PDF Enhancer

218

COMPUTER PROBLEMS

The following problems are designed to be solved with a computer. Write each

program so that it can be used with either SI or U.S. customary units.

3.C1

Shaft AB consists of n homogeneous cylindrical elements, which can

be solid or hollow. Its end A is fixed, while its end B is free, and it is subjected

to the loading shown. The length of element i is denoted by L

, its outer

diameter by OD

, its inner diameter by ID

, its modulus of rigidity by G

, and

the torque applied to its right end by T

, the magnitude T

of this torque being

assumed to be positive if T

is observed as counterclockwise from end B and

negative otherwise. (Note that ID

5 0 if the element is solid.) (a) Write a

computer program that can be used to determine the maximum shearing

stress in each element, the angle of twist of each element, and the angle of

twist of the entire shaft. (b) Use this program to solve Probs. 3.35 and 3.38.

Element 1

Element n

Fig. P3.C1

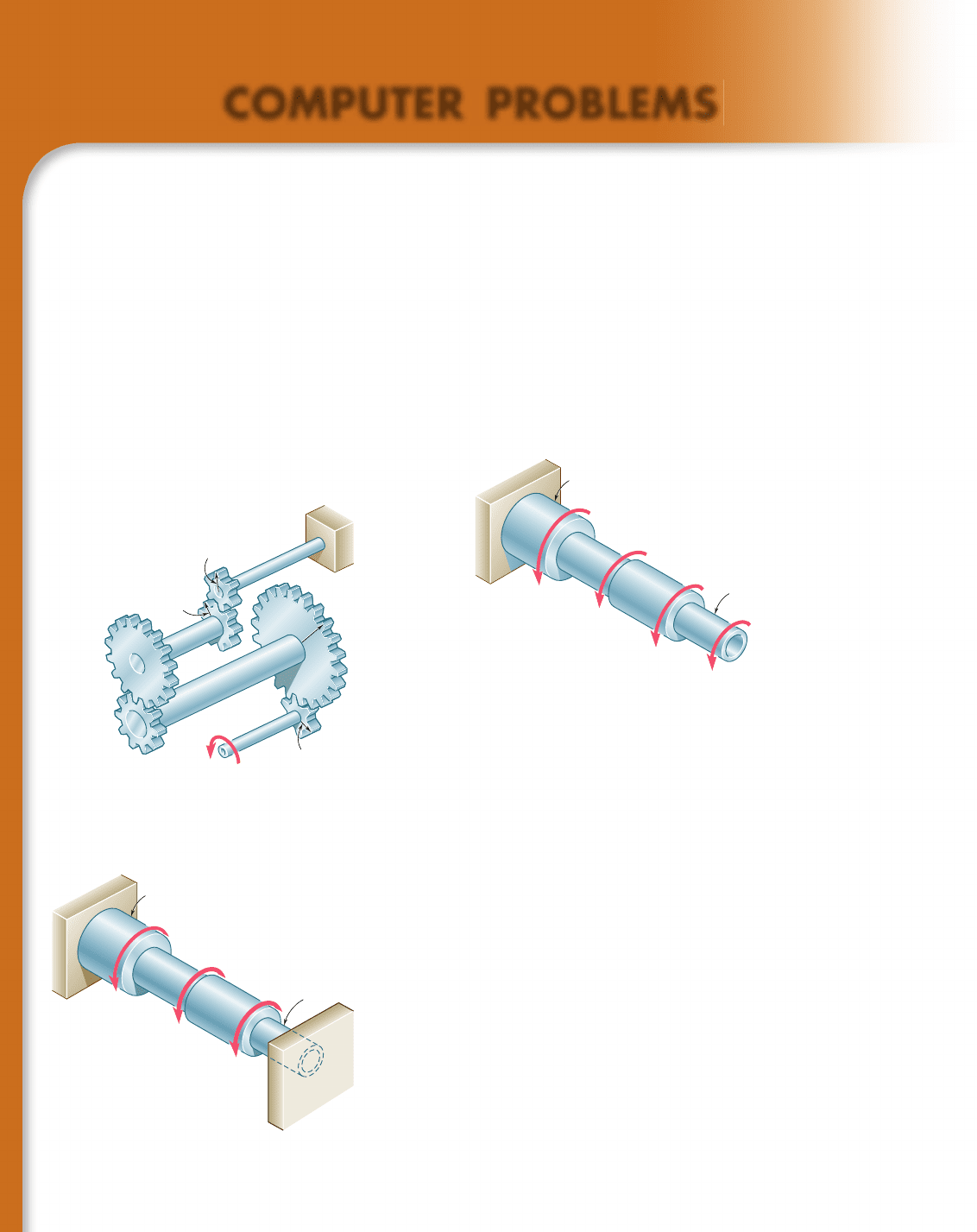
3.C2 The assembly shown consists of n cylindrical shafts, which can be

solid or hollow, connected by gears and supported by brackets (not shown).

End A

of the first shaft is free and is subjected to a torque T

, while end

of the last shaft is fixed. The length of shaft A

is denoted by L

, its

outer diameter by OD

, its inner diameter by ID

, and its modulus of rigidity

by G

. (Note that ID

5 0 if the element is solid.) The radius of gear A

denoted by a

, and the radius of gear B

by b

. (a) Write a computer program

that can be used to determine the maximum shearing stress in each shaft,

the angle of twist of each shaft, and the angle through which end A

rotates.

(b) Use this program to solve Probs. 3.41 and 3.44.

3.C3 Shaft AB consists of n homogeneous cylindrical elements, which can

be solid or hollow. Both of its ends are fixed, and it is subjected to the load-

ing shown. The length of element i is denoted by L

, its outer diameter by

, its inner diameter by ID

, its modulus of rigidity by G

, and the torque

applied to its right end by T

, the magnitude T

of this torque being assumed

to be positive if T

is observed as counterclockwise from end B and negative

otherwise. Note that ID

5 0 if the element is solid and also that T

5 0.

Write a computer program that can be used to determine the reactions at A

and B, the maximum shearing stress in each element, and the angle of twist

of each element. Use this program (a) to solve Prob. 3.155, (b) to determine

the maximum shearing stress in the shaft of Example 3.05.

n –1

Fig. P3.C2

Element 1

Element n

Fig. P3.C3

bee80288_ch03_140-219.indd Page 218 9/21/10 3:13:00 PM user-f499bee80288_ch03_140-219.indd Page 218 9/21/10 3:13:00 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

219

Computer Problems

3.C4 The homogeneous, solid cylindrical shaft AB has a length L, a

diameter d, a modulus of rigidity G, and a yield strength t

. It is subjected

to a torque T that is gradually increased from zero until the angle of twist

of the shaft has reached a maximum value f

and then decreased back to

zero. (a) Write a computer program that, for each of 16 values of f

equally

spaced over a range extending from 0 to a value 3 times as large as the

angle of twist at the onset of yield, can be used to determine the maximum

value T

of the torque, the radius of the elastic core, the maximum shearing

stress, the permanent twist, and the residual shearing stress both at the

surface of the shaft and at the interface of the elastic core and the plastic

region. (b) Use this program to obtain approximate answers to Probs. 3.114,

3.115, 3.116.

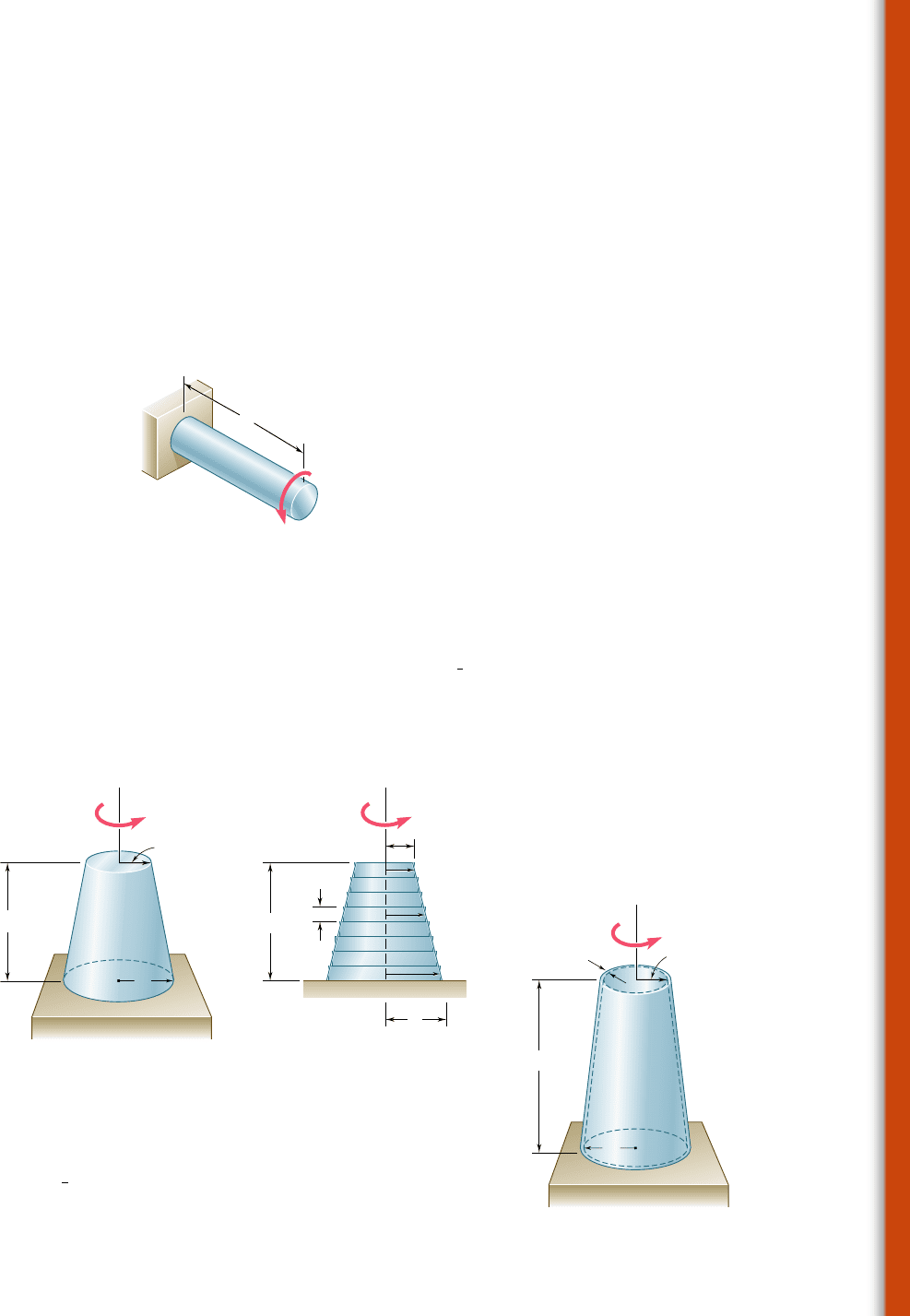
3.C5 The exact expression is given in Prob. 3.61 for the angle of twist of

the solid tapered shaft AB when a torque T is applied as shown. Derive an

approximate expression for the angle of twist by replacing the tapered shaft

by n cylindrical shafts of equal length and of radius r

n 1 i 2

(cyn),

where i 5 1, 2, . . ., n. Using for T, L, G, and c values of your choice, deter-

mine the percentage error in the approximate expression when (a) n 5 4,

(b) n 5 8, (c) n 5 20, (d) n 5 100.

Fig. P3.C4

L/n

Fig. P3.C5

3.C6 A torque T is applied as shown to the long, hollow, tapered shaft AB

of uniform thickness t. Derive an approximate expression for the angle of twist

by replacing the tapered shaft by n cylindrical rings of equal length and of radius

n 1 i 2

(cyn), where i 5 1, 2, . . ., n. Using for T, L, G, c, and t values

of your choice, determine the percentage error in the approximate expression

when (a) n 5 4, (b) n 5 8, (c) n 5 20, (d) n 5 100.

Fig. P3.C6

bee80288_ch03_140-219.indd Page 219 9/21/10 3:13:10 PM user-f499bee80288_ch03_140-219.indd Page 219 9/21/10 3:13:10 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

The athlete shown holds the barbell

with his hands placed at equal

distances from the weights. This results

in pure bending in the center portion

of the bar. The normal stresses and the

curvature resulting from pure bending

will be determined in this chapter.

220

bee80288_ch04_220-313.indd Page 220 10/26/10 4:21:38 PM user-f499bee80288_ch04_220-313.indd Page 220 10/26/10 4:21:38 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

CHAPTER

Pure Bending

221

bee80288_ch04_220-313.indd Page 221 10/26/10 4:24:22 PM user-f499bee80288_ch04_220-313.indd Page 221 10/26/10 4:24:22 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

222

Chapter 4 Pure Bending

4.1 Introduction

4.2 Symmetric Member in Pure

Bending

4.3 Deformations in a Symmetric

Member in Pure Bending

4.4 Stresses and Deformations in

the Elastic Range

4.5 Deformations in a Transverse

Cross Section

4.6 Bending of Members Made

of Several Materials

4.7 Stress Concentrations

*4.8 Plastic Deformations

*4.9 Members Made of Elastoplastic

Material

*4.10 Plastic Deformations of Members

with a Single Plane of Symmetry

*4.11 Residual Stresses

4.12 Eccentric Axial Loading in a

Plane of Symmetry

4.13 Unsymmetric Bending

4.14 General Case of Eccentric Axial

*4.15 Bending of Curved Members

4.1 INTRODUCTION

In the preceding chapters you studied how to determine the stresses

in prismatic members subjected to axial loads or to twisting couples.

In this chapter and in the following two you will analyze the stresses

and strains in prismatic members subjected to bending. Bending is

a major concept used in the design of many machine and structural

components, such as beams and girders.

This chapter will be devoted to the analysis of prismatic mem-

bers subjected to equal and opposite couples M and M9 acting in

the same longitudinal plane. Such members are said to be in pure

bending. In most of the chapter, the members will be assumed to

possess a plane of symmetry and the couples M and M9 to be acting

in that plane (Fig. 4.1).

Fig. 4.1 Member in pure bending.

12 in. 26 in. 12 in.

M' = 960 lb · in.M = 960 lb · in.

= 80 lb

80 lb80 lb

= 80 lb

(a)

(b)

Fig. 4.2 Beam in which portion CD

is in pure bending.

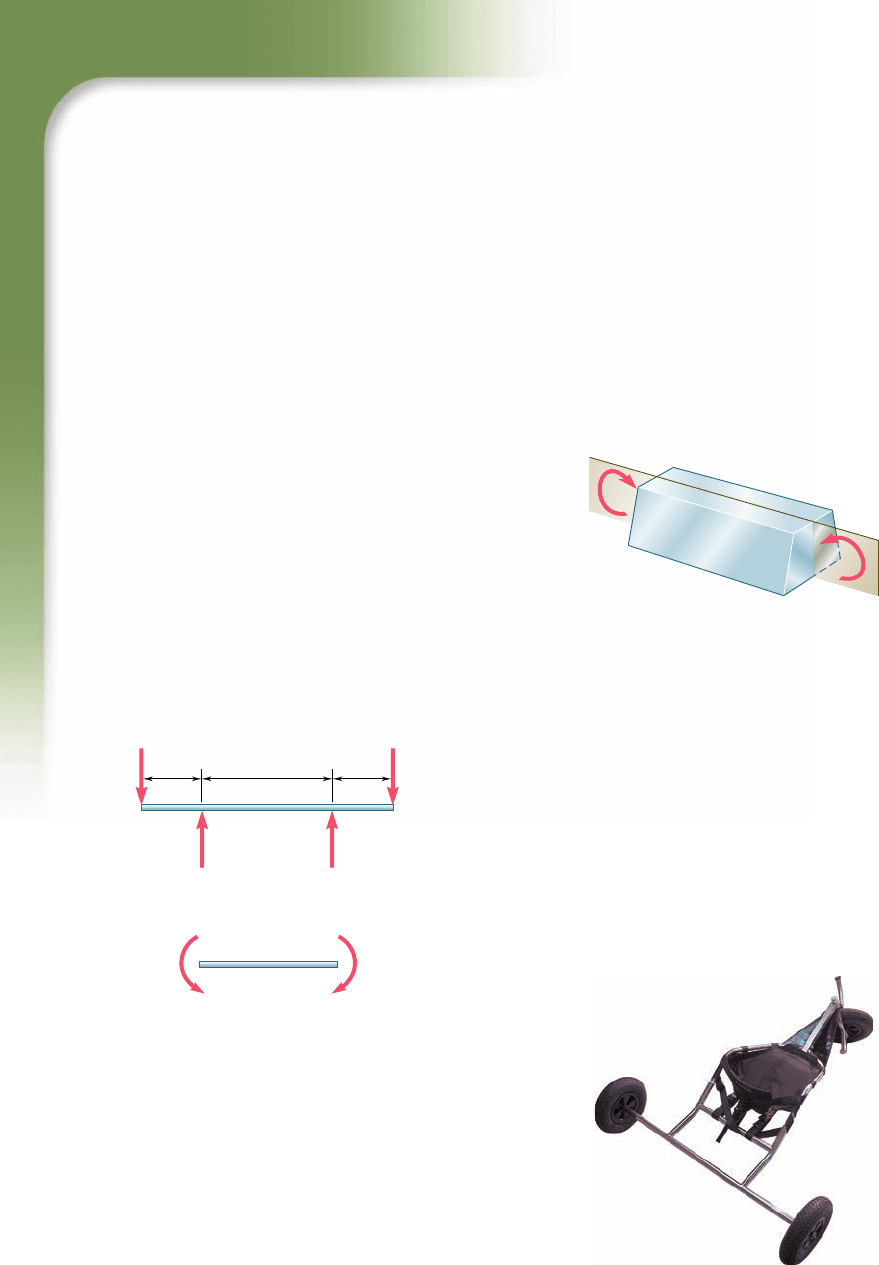
Photo 4.1 For the sport buggy

shown, the center portion of the rear

axle is in pure bending.

An example of pure bending is provided by the bar of a typical bar-

bell as it is held overhead by a weight lifter as shown in the opening

photo for this chapter. The bar carries equal weights at equal dis-

tances from the hands of the weight lifter. Because of the symmetry

of the free-body diagram of the bar (Fig. 4.2a), the reactions at the

hands must be equal and opposite to the weights. Therefore, as far

as the middle portion CD of the bar is concerned, the weights and

the reactions can be replaced by two equal and opposite 960-lb ? in.

couples (Fig. 4.2b), showing that the middle portion of the bar is in

pure bending. A similar analysis of the axle of a small sport buggy

(Photo 4.1) would show that, between the two points where it is

attached to the frame, the axle is in pure bending.

bee80288_ch04_220-313.indd Page 222 11/11/10 3:03:05 PM user-f499bee80288_ch04_220-313.indd Page 222 11/11/10 3:03:05 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch04

Apago PDF Enhancer

223

As interesting as the direct applications of pure bending may

be, devoting an entire chapter to its study would not be justified if

it were not for the fact that the results obtained will be used in the

analysis of other types of loadings as well, such as eccentric axial

loadings and transverse loadings.

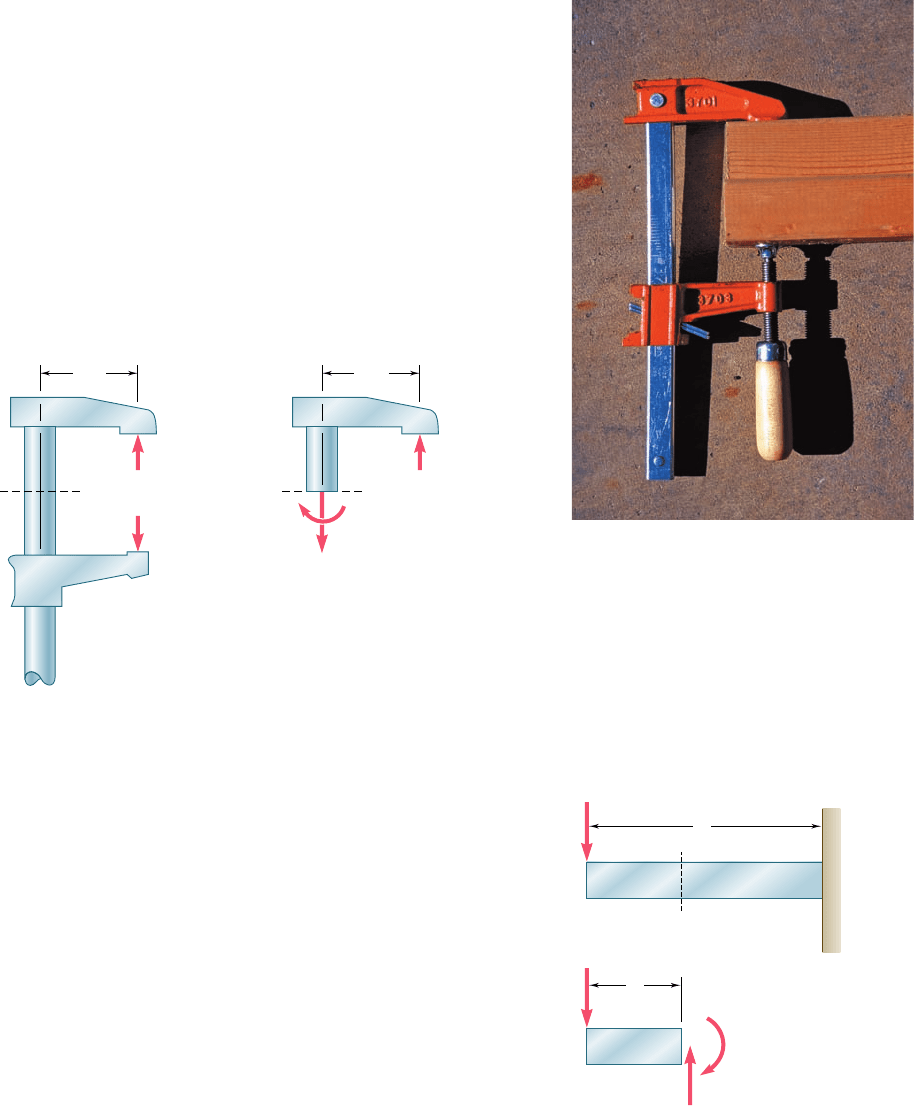
Photo 4.2 shows a 12-in. steel bar clamp used to exert 150-lb

forces on two pieces of lumber as they are being glued together. Fig-

ure 4.3a shows the equal and opposite forces exerted by the lumber

on the clamp. These forces result in an eccentric loading of the straight

portion of the clamp. In Fig. 4.3b a section CC9 has been passed

through the clamp and a free-body diagram has been drawn of the

upper half of the clamp, from which we conclude that the internal

forces in the section are equivalent to a 150-lb axial tensile force P

and a 750-lb ? in. couple M. We can thus combine our knowledge of

the stresses under a centric load and the results of our forthcoming

analysis of stresses in pure bending to obtain the distribution of stresses

under an eccentric load. This will be further discussed in Sec. 4.12.

4.1 Introduction

Photo 4.2 Clamp used to glue lumber

pieces together.

5 in.

CC' CC'

P'  150 lb

P  150 lb

P'  150 lb

M  750 lb · in.

P  150 lb

5 in.

(a)(b)

Fig. 4.3 Forces exerted on clamp.

The study of pure bending will also play an essential role in the

study of beams, i.e., the study of prismatic members subjected to

various types of transverse loads. Consider, for instance, a cantilever

beam AB supporting a concentrated load P at its free end (Fig. 4.4a).

If we pass a section through C at a distance x from A, we observe

from the free-body diagram of AC (Fig. 4.4b) that the internal forces

in the section consist of a force P9 equal and opposite to P and a

couple M of magnitude M 5 Px. The distribution of normal stresses

in the section can be obtained from the couple M as if the beam

were in pure bending. On the other hand, the shearing stresses in

the section depend on the force P9, and you will learn in Chap. 6

how to determine their distribution over a given section.

The first part of the chapter is devoted to the analysis of the

stresses and deformations caused by pure bending in a homogeneous

member possessing a plane of symmetry and made of a material fol-

lowing Hooke’s law. In a preliminary discussion of the stresses due

to bending (Sec. 4.2), the methods of statics will be used to derive

(a)

(b)

Fig. 4.4 Cantilever beam, not in

pure bending.

bee80288_ch04_220-313.indd Page 223 10/26/10 4:24:41 PM user-f499bee80288_ch04_220-313.indd Page 223 10/26/10 4:24:41 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

224

Pure Bending

three fundamental equations which must be satisfied by the normal

stresses in any given cross section of the member. In Sec. 4.3, it will

be proved that transverse sections remain plane in a member sub-

jected to pure bending, while in Sec. 4.4 formulas will be developed

that can be used to determine the normal stresses, as well as the

radius of curvature for that member within the elastic range.

In Sec. 4.6, you will study the stresses and deformations in com-

posite members made of more than one material, such as reinforced-

concrete beams, which utilize the best features of steel and concrete

and are extensively used in the construction of buildings and bridges.

You will learn to draw a transformed section representing the section

of a member made of a homogeneous material that undergoes the

same deformations as the composite member under the same load-

ing. The transformed section will be used to find the stresses and

deformations in the original composite member. Section 4.7 is

devoted to the determination of the stress concentrations occurring

at locations where the cross section of a member undergoes a sudden

change.

In the next part of the chapter you will study plastic deforma-

tions in bending, i.e., the deformations of members which are made

of a material which does not follow Hooke’s law and are subjected

to bending. After a general discussion of the deformations of such

members (Sec. 4.8), you will investigate the stresses and deforma-

tions in members made of an elastoplastic material (Sec. 4.9). Start-

ing with the maximum elastic moment M

, which corresponds to the

onset of yield, you will consider the effects of increasingly larger

moments until the plastic moment M

is reached, at which time the

member has yielded fully. You will also learn to determine the per-

manent deformations and residual stresses that result from such load-

ings (Sec. 4.11). It should be noted that during the past half-century

the elastoplastic property of steel has been widely used to produce

designs resulting in both improved safety and economy.

In Sec. 4.12, you will learn to analyze an eccentric axial loading

in a plane of symmetry, such as the one shown in Fig. 4.4, by super-

posing the stresses due to pure bending and the stresses due to a

centric axial loading.

Your study of the bending of prismatic members will conclude

with the analysis of unsymmetric bending (Sec. 4.13), and the study

of the general case of eccentric axial loading (Sec. 4.14). The final

section of the chapter will be devoted to the determination of the

stresses in curved members (Sec. 4.15).

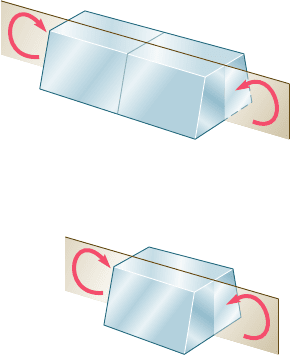
4.2 SYMMETRIC MEMBER IN PURE BENDING

Consider a prismatic member AB possessing a plane of symmetry

and subjected to equal and opposite couples M and M9 acting in that

plane (Fig. 4.5a). We observe that if a section is passed through the

member AB at some arbitrary point C, the conditions of equilibrium

of the portion AC of the member require that the internal forces in

the section be equivalent to the couple M (Fig. 4.5b). Thus, the

internal forces in any cross section of a symmetric member in pure

bending are equivalent to a couple. The moment M of that couple

(b)

Fig. 4.5 Member in pure bending.

(a)

bee80288_ch04_220-313.indd Page 224 10/26/10 4:24:49 PM user-f499bee80288_ch04_220-313.indd Page 224 10/26/10 4:24:49 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

225

is referred to as the bending moment in the section. Following the

usual convention, a positive sign will be assigned to M when the

member is bent as shown in Fig. 4.5a, i.e., when the concavity of

the beam faces upward, and a negative sign otherwise.

Denoting by s

the normal stress at a given point of the cross

section and by t

and t

the components of the shearing stress, we

express that the system of the elementary internal forces exerted on

the section is equivalent to the couple M (Fig. 4.6).





Fig. 4.6

We recall from statics that a couple M actually consists of two

equal and opposite forces. The sum of the components of these

forces in any direction is therefore equal to zero. Moreover, the

moment of the couple is the same about any axis perpendicular to

its plane, and is zero about any axis contained in that plane. Selecting

arbitrarily the z axis as shown in Fig. 4.6, we express the equivalence

of the elementary internal forces and of the couple M by writing that

the sums of the components and of the moments of the elementary

forces are equal to the corresponding components and moments of

the couple M:

x components: es

dA 5 0 (4.1)

moments about y axis: ezs

dA 5 0 (4.2)

moments about z axis: e(2ys

dA) 5 M (4.3)

Three additional equations could be obtained by setting equal to zero

the sums of the y components, z components, and moments about

the x axis, but these equations would involve only the components

of the shearing stress and, as you will see in the next section, the

components of the shearing stress are both equal to zero.

Two remarks should be made at this point: (1) The minus sign

in Eq. (4.3) is due to the fact that a tensile stress (s

. 0) leads to

a negative moment (clockwise) of the normal force s

dA about the

z axis. (2) Equation (4.2) could have been anticipated, since the

application of couples in the plane of symmetry of member AB will

result in a distribution of normal stresses that is symmetric about the

y axis.

Once more, we note that the actual distribution of stresses in

a given cross section cannot be determined from statics alone. It is

statically indeterminate and may be obtained only by analyzing the

deformations produced in the member.

4.2 Symmetric Member in Pure Bending

bee80288_ch04_220-313.indd Page 225 10/26/10 4:24:51 PM user-f499bee80288_ch04_220-313.indd Page 225 10/26/10 4:24:51 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles

Apago PDF Enhancer

226

Pure Bending

4.3 DEFORMATIONS IN A SYMMETRIC MEMBER

IN PURE BENDING

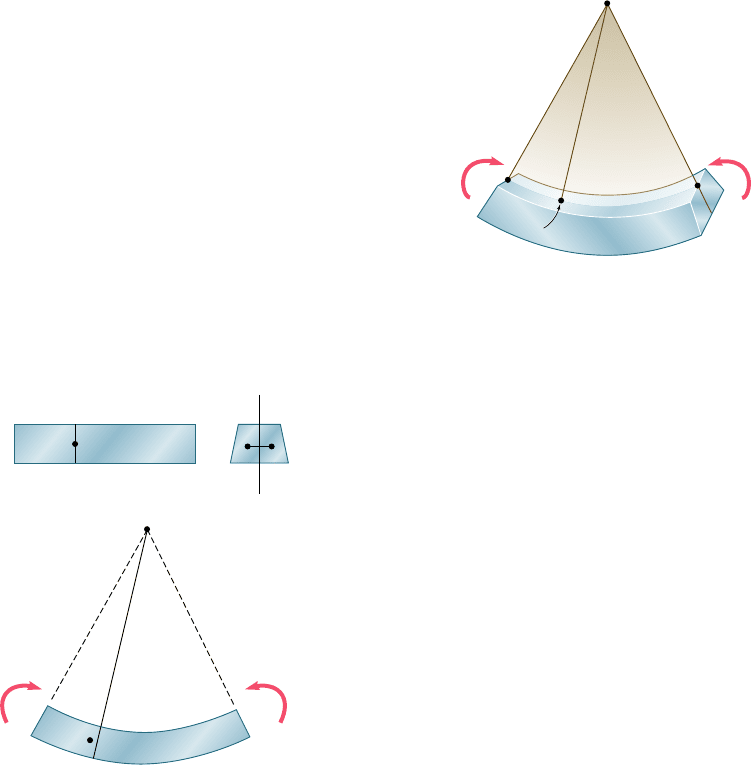
Let us now analyze the deformations of a prismatic member possess-

ing a plane of symmetry and subjected at its ends to equal and oppo-

site couples M and M9 acting in the plane of symmetry. The member

will bend under the action of the couples, but will remain symmetric

with respect to that plane (Fig. 4.7). Moreover, since the bending

moment M is the same in any cross section, the member will bend

uniformly. Thus, the line AB along which the upper face of the mem-

ber intersects the plane of the couples will have a constant curvature.

In other words, the line AB, which was originally a straight line, will

be transformed into a circle of center C, and so will the line A9B9

(not shown in the figure) along which the lower face of the member

intersects the plane of symmetry. We also note that the line AB will

decrease in length when the member is bent as shown in the figure,

i.e., when M . 0, while A9B9 will become longer.

M M

ⴕ

⬘

Fig. 4.7 Deformation of member in

pure bending.

Next we will prove that any cross section perpendicular to the

axis of the member remains plane, and that the plane of the section

passes through C. If this were not the case, we could find a point E

of the original section through D (Fig. 4.8a) which, after the member

has been bent, would not lie in the plane perpendicular to the plane

of symmetry that contains line CD (Fig. 4.8b). But, because of the

symmetry of the member, there would be another point E9 that would

be transformed exactly in the same way. Let us assume that, after the

beam has been bent, both points would be located to the left of the

plane defined by CD, as shown in Fig. 4.8b. Since the bending moment

M is the same throughout the member, a similar situation would pre-

vail in any other cross section, and the points corresponding to E and

E9 would also move to the left. Thus, an observer at A would conclude

that the loading causes the points E and E9 in the various cross sec-

tions to move forward (toward the observer). But an observer at B, to

whom the loading looks the same, and who observes the points E and

E9 in the same positions (except that they are now inverted) would

reach the opposite conclusion. This inconsistency leads us to conclude

that E and E9 will lie in the plane defined by CD and, therefore, that

the section remains plane and passes through C. We should note,

M' M

E⬘

EE⬘

(a)

(b)

Fig. 4.8

bee80288_ch04_220-313.indd Page 226 10/26/10 4:24:54 PM user-f499bee80288_ch04_220-313.indd Page 226 10/26/10 4:24:54 PM user-f499 /Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles/Volumes/201/MHDQ251/bee80288_disk1of1/0073380288/bee80288_pagefiles