Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

3.117 After the solid shaft of Prob. 3.116 has been loaded and unloaded

as described in that problem, a torque T

of sense opposite to

the original torque T is applied to the shaft. Assuming no change

in the value of f

, determine the angle of twist f

for which

yield is initiated in this second loading and compare it with the

angle f

for which the shaft started to yield in the original

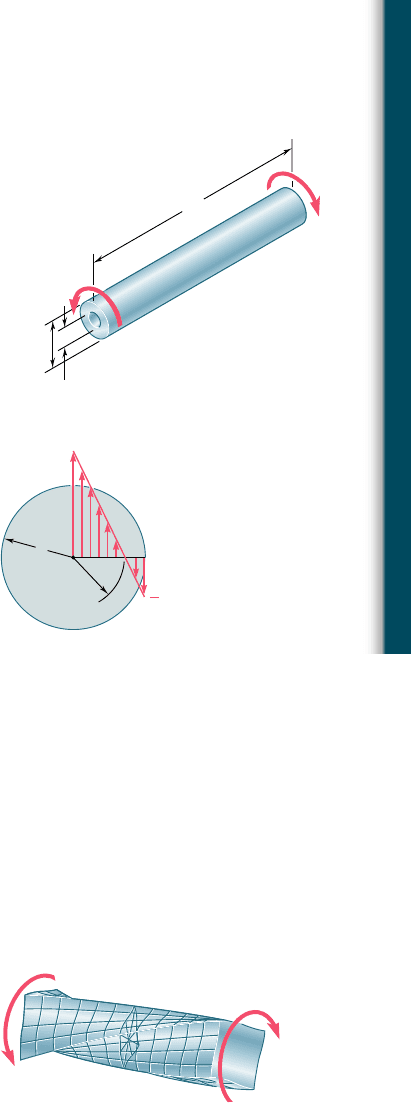
3.118 The hollow shaft shown is made of a steel that is assumed to be

elastoplastic with t

5 145 MPa and G 5 77.2 GPa. The magni-

tude T of the torques is slowly increased until the plastic zone first

reaches the inner surface of the shaft; the torques are then removed.

Determine the magnitude and location of the maximum residual

shearing stress in the rod.

3.119 In Prob. 3.118, determine the permanent angle of twist of the rod.

3.120 A torque T applied to a solid rod made of an elastoplastic material

is increased until the rod is fully plastic and then removed.

(a) Show that the distribution of residual shearing stresses is as

represented in the figure. (b) Determine the magnitude of the

torque due to the stresses acting on the portion of the rod located

within a circle of radius c

5 m

25 mm

60 mm

Fig. P3.118

␶

Fig. P3.120

*3.12 TORSION OF NONCIRCULAR MEMBERS

The formulas obtained in Secs. 3.3 and 3.4 for the distributions of

strain and stress under a torsional loading apply only to members with

a circular cross section. Indeed, their derivation was based on the

assumption that the cross section of the member remained plane and

undistorted, and we saw in Sec. 3.3 that the validity of this assumption

depends upon the axisymmetry of the member, i.e., upon the fact

that its appearance remains the same when it is viewed from a fixed

position and rotated about its axis through an arbitrary angle.

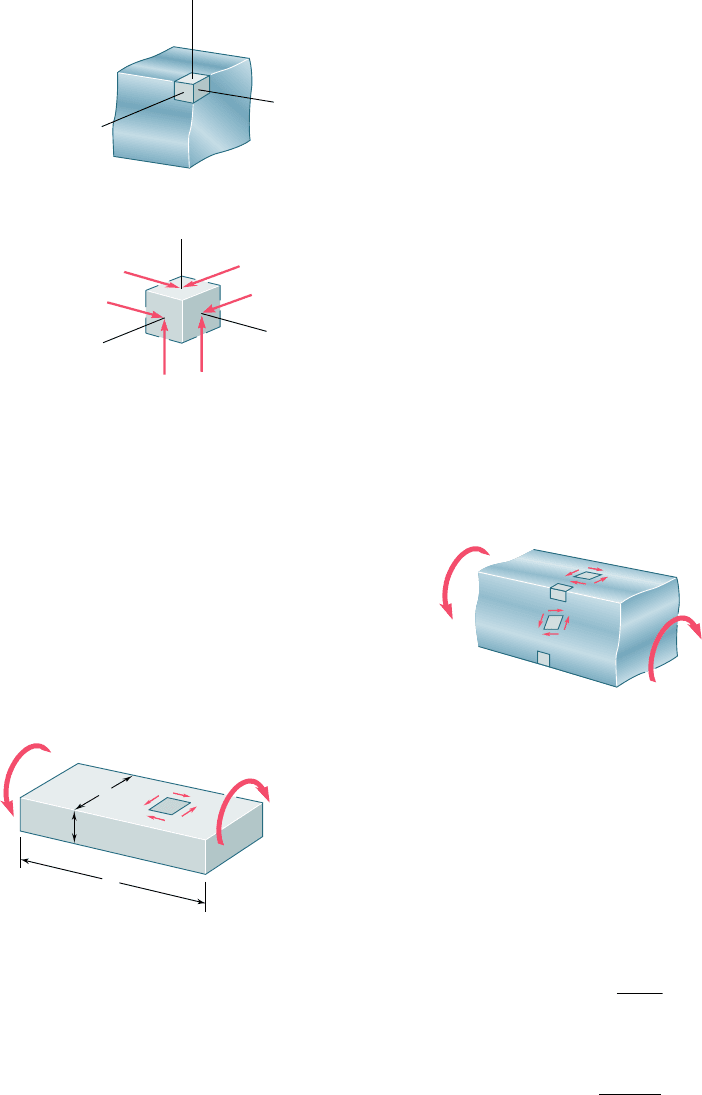
A square bar, on the other hand, retains the same appearance

only when it is rotated through 908 or 1808. Following a line of

reasoning similar to that used in Sec. 3.3, one could show that the

diagonals of the square cross section of the bar and the lines joining

the midpoints of the sides of that section remain straight (Fig. 3.42).

However, because of the lack of axisymmetry of the bar, any other

line drawn in its cross section will deform when the bar is twisted,

and the cross section itself will be warped out of its original

plane.

It follows that Eqs. (3.4) and (3.6), which define, respectively,

the distributions of strain and stress in an elastic circular shaft, cannot

be used for noncircular members. For example, it would be wrong

to assume that the shearing stress in the cross section of a square bar

varies linearly with the distance from the axis of the bar and is, there-

fore, largest at the corners of the cross section. As you will see pres-

ently, the shearing stress is actually zero at these points.

Fig. 3.42 Twisting of shaft with

square cross section.

197

3.12 Torsion of Noncircular Members

bee80288_ch03_140-219.indd Page 197 11/2/10 3:07:29 PM user-f499bee80288_ch03_140-219.indd Page 197 11/2/10 3:07:29 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

198

Torsion

Consider a small cubic element located at a corner of the cross

section of a square bar in torsion and select coordinate axes parallel

to the edges of the element (Fig. 3.43a). Since the face of the ele-

ment perpendicular to the y axis is part of the free surface of the

bar, all stresses on this face must be zero. Referring to Fig. 3.43b,

we write

5 0 t

5 0 (3.40)

For the same reason, all stresses on the face of the element perpen-

dicular to the z axis must be zero, and we write

5 0 t

5 0 (3.41)

It follows from the first of Eqs. (3.40) and the first of Eqs. (3.41)

that

5 0 t

5 0 (3.42)

Thus, both components of the shearing stress on the face of the element

perpendicular to the axis of the bar are zero. We conclude that there

is no shearing stress at the corners of the cross section of the bar.

By twisting a rubber model of a square bar, one easily verifies

that no deformations—and, thus, no stresses—occur along the edges

of the bar, while the largest deformations—and, thus, the largest

stresses—occur along the center line of each of the faces of the bar

(Fig. 3.44).

␶

(a)

(b)

Fig. 3.43 Corner element.

max

␶

max

␶

Fig. 3.44 Deformation of square bar.

†See S. P. Timoshenko and J. N. Goodier, Theory of Elasticity, 3d ed., McGraw-Hill, New

York, 1969, sec. 109.

max

␶

Fig. 3.45 Shaft with rectangular cross

section.

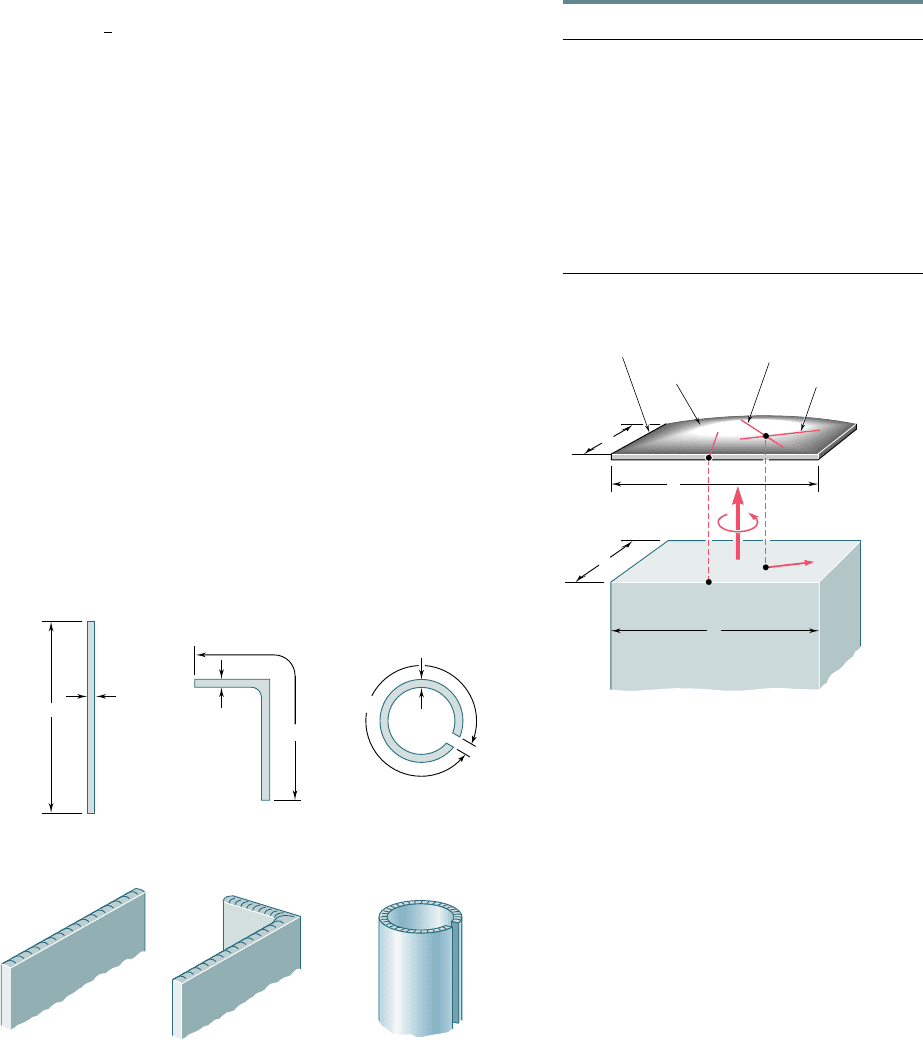
The determination of the stresses in noncircular members sub-

jected to a torsional loading is beyond the scope of this text. How-

ever, results obtained from the mathematical theory of elasticity for

straight bars with a uniform rectangular cross section will be indi-

cated here for convenience.† Denoting by L the length of the bar,

by a and b, respectively, the wider and narrower side of its cross

section, and by T the magnitude of the torques applied to the bar

(Fig. 3.45), we find that the maximum shearing stress occurs along

the center line of the wider face of the bar and is equal to

max

(3.43)

The angle of twist, on the other hand, may be expressed as

f 5

(3.44)

bee80288_ch03_140-219.indd Page 198 11/2/10 3:07:38 PM user-f499bee80288_ch03_140-219.indd Page 198 11/2/10 3:07:38 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

199

The coefficients c

and c

depend only upon the ratio ayb and are

given in Table 3.1 for a number of values of that ratio. Note that

Eqs. (3.43) and (3.44) are valid only within the elastic range.

We note from Table 3.1 that for ayb $ 5, the coefficients c

and

are equal. It may be shown that for such values of ayb, we have

5 c

1 2 0.630b

(for ayb % 5 only) (3.45)

The distribution of shearing stresses in a noncircular member

may be visualized more easily by using the membrane analogy. A homo-

geneous elastic membrane attached to a fixed frame and subjected to

a uniform pressure on one of its sides happens to constitute an analog

of the bar in torsion, i.e., the determination of the deformation of the

membrane depends upon the solution of the same partial differential

equation as the determination of the shearing stresses in the bar.† More

specifically, if Q is a point of the cross section of the bar and Q9 the

corresponding point of the membrane (Fig. 3.46), the shearing stress

t at Q will have the same direction as the horizontal tangent to the

membrane at Q9, and its magnitude will be proportional to the maxi-

mum slope of the membrane at Q9.‡ Furthermore, the applied torque

will be proportional to the volume between the membrane and the

plane of the fixed frame. In the case of the membrane of Fig. 3.46,

which is attached to a rectangular frame, the steepest slope occurs at

the midpoint N9 of the larger side of the frame. Thus, we verify that

the maximum shearing stress in a bar of rectangular cross section will

occur at the midpoint N of the larger side of that section.

The membrane analogy may be used just as effectively to visu-

alize the shearing stresses in any straight bar of uniform, noncircular

cross section. In particular, let us consider several thin-walled mem-

bers with the cross sections shown in Fig. 3.47, which are subjected

TABLE 3.1. Coefficients for

Rectangular Bars in Torsion

a/b c

1.0 0.208 0.1406

1.2 0.219 0.1661

1.5 0.231 0.1958

2.0 0.246 0.229

2.5 0.258 0.249

3.0 0.267 0.263

4.0 0.282 0.281

5.0 0.291 0.291

10.0 0.312 0.312

` 0.333 0.333

†See ibid. Sec. 107.

‡This is the slope measured in a direction perpendicular to the horizontal tangent at Q9.

Rectangular frame

Tangent of

max. slope

Membrane

Horizontal

tangent



Fig. 3.46 Application of membrane

analogy to shaft with rectangular cross

section.

Fig. 3.47 Various thin-walled members.

3.12 Torsion of Noncircular Members

bee80288_ch03_140-219.indd Page 199 11/2/10 12:48:32 AM user-f499bee80288_ch03_140-219.indd Page 199 11/2/10 12:48:32 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

200

Torsion

to the same torque. Using the membrane analogy to help us visualize

the shearing stresses, we note that, since the same torque is applied

to each member, the same volume will be located under each mem-

brane, and the maximum slope will be about the same in each case.

Thus, for a thin-walled member of uniform thickness and arbitrary

shape, the maximum shearing stress is the same as for a rectangular

bar with a very large value of ayb and may be determined from Eq.

(3.43) with c

5 0.333.†

*3.13 THIN-WALLED HOLLOW SHAFTS

In the preceding section we saw that the determination of stresses

in noncircular members generally requires the use of advanced

mathematical methods. In the case of thin-walled hollow noncircular

shafts, however, a good approximation of the distribution of stresses

in the shaft can be obtained by a simple computation.

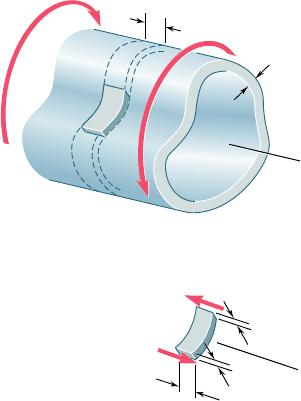
Consider a hollow cylindrical member of noncircular section

subjected to a torsional loading (Fig. 3.48).‡ While the thickness t

of the wall may vary within a transverse section, it will be assumed

that it remains small compared to the other dimensions of the mem-

ber. We now detach from the member the colored portion of wall

AB bounded by two transverse planes at a distance Dx from each

other, and by two longitudinal planes perpendicular to the wall. Since

the portion AB is in equilibrium, the sum of the forces exerted on

it in the longitudinal x direction must be zero (Fig. 3.49). But the

only forces involved are the shearing forces F

and F

exerted on

the ends of portion AB. We have therefore

5 0: F

2 F

5 0 (3.46)

We now express F

as the product of the longitudinal shearing

stress t

on the small face at A and of the area t

Dx of that face:

5 t

Dx)

We note that, while the shearing stress is independent of the x coor-

dinate of the point considered, it may vary across the wall; thus, t

represents the average value of the stress computed across the wall.

Expressing F

in a similar way and substituting for F

and F

into

(3.46), we write

Dx) 2 t

Dx) 5 0

or t

5 t

(3.47)

Since A and B were chosen arbitrarily, Eq. (3.47) expresses that the

product tt of the longitudinal shearing stress t and of the wall thick-

ness t is constant throughout the member. Denoting this product by

q, we have

q 5 tt 5 constant (3.48)

†It could also be shown that the angle of twist may be determined from Eq. (3.44) with

5 0.333.

‡The wall of the member must enclose a single cavity and must not be slit open. In other

words, the member should be topologically equivalent to a hollow circular shaft.

x

Fig. 3.48 Thin-walled hollow shaft.

x

Fig. 3.49 Segment of

thin-walled hollow shaft.

bee80288_ch03_140-219.indd Page 200 9/21/10 3:09:04 PM user-f499bee80288_ch03_140-219.indd Page 200 9/21/10 3:09:04 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

201

We now detach a small element from the wall portion AB (Fig.

3.50). Since the upper and lower faces of this element are part of

the free surface of the hollow member, the stresses on these faces

are equal to zero. Recalling relations (1.21) and (1.22) of Sec. 1.12,

it follows that the stress components indicated on the other faces by

dashed arrows are also zero, while those represented by solid arrows

are equal. Thus, the shearing stress at any point of a transverse sec-

tion of the hollow member is parallel to the wall surface (Fig. 3.51)

and its average value computed across the wall satisfies Eq. (3.48).

At this point we can note an analogy between the distribution

of the shearing stresses t in the transverse section of a thin-walled

hollow shaft and the distribution of the velocities v in water flowing

through a closed channel of unit depth and variable width. While

the velocity v of the water varies from point to point on account of

the variation in the width t of the channel, the rate of flow, q 5 vt,

remains constant throughout the channel, just as tt in Eq. (3.48).

Because of this analogy, the product q 5 tt is referred to as the shear

flow in the wall of the hollow shaft.

We will now derive a relation between the torque T applied to

a hollow member and the shear flow q in its wall. We consider a

small element of the wall section, of length ds (Fig. 3.52). The area

of the element is dA 5 t ds, and the magnitude of the shearing force

dF exerted on the element is

dF 5 t dA 5 t(t ds) 5 (tt) ds 5 q ds (3.49)

The moment dM

of this force about an arbitrary point O within the

cavity of the member may be obtained by multiplying dF by the per-

pendicular distance p from O to the line of action of dF. We have

5 p dF 5 p(q ds) 5 q(p ds) (3.50)

But the product p ds is equal to twice the area dA of the colored

triangle in Fig. 3.53. We thus have

5 q(2dA) (3.51)

Since the integral around the wall section of the left-hand member

of Eq. (3.51) represents the sum of the moments of all the elemen-

tary shearing forces exerted on the wall section, and since this sum

is equal to the torque T applied to the hollow member, we have

T 5

q12dA2

The shear flow q being a constant, we write

T 5 2qA (3.52)

where A is the area bounded by the center line of the wall cross

section (Fig. 3.54).

The shearing stress t at any given point of the wall may be

expressed in terms of the torque T if we substitute for q from (3.48)

into (3.52) and solve for t the equation obtained. We have

t 5

A (3.53)

x

s



Fig. 3.50 Small element

from segment.



Fig. 3.51 Direction of shearing

stress on cross section.

3.13 Thin-Walled Hollow Shafts

Fig. 3.52

Fig. 3.53



Fig. 3.54 Area for shear flow.

bee80288_ch03_140-219.indd Page 201 9/21/10 3:09:08 PM user-f499bee80288_ch03_140-219.indd Page 201 9/21/10 3:09:08 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

202

Torsion

where t is the wall thickness at the point considered and A the area

bounded by the center line. We recall that t represents the average

value of the shearing stress across the wall. However, for elastic

deformations the distribution of stresses across the wall may be

assumed uniform, and Eq. (3.53) will yield the actual value of the

shearing stress at a given point of the wall.

The angle of twist of a thin-walled hollow shaft may be obtained

by using the method of energy (Chap. 11). Assuming an elastic defor-

mation, it may be shown† that the angle of twist of a thin-walled

shaft of length L and modulus of rigidity G is

f 5

(3.54)

where the integral is computed along the center line of the wall

section.

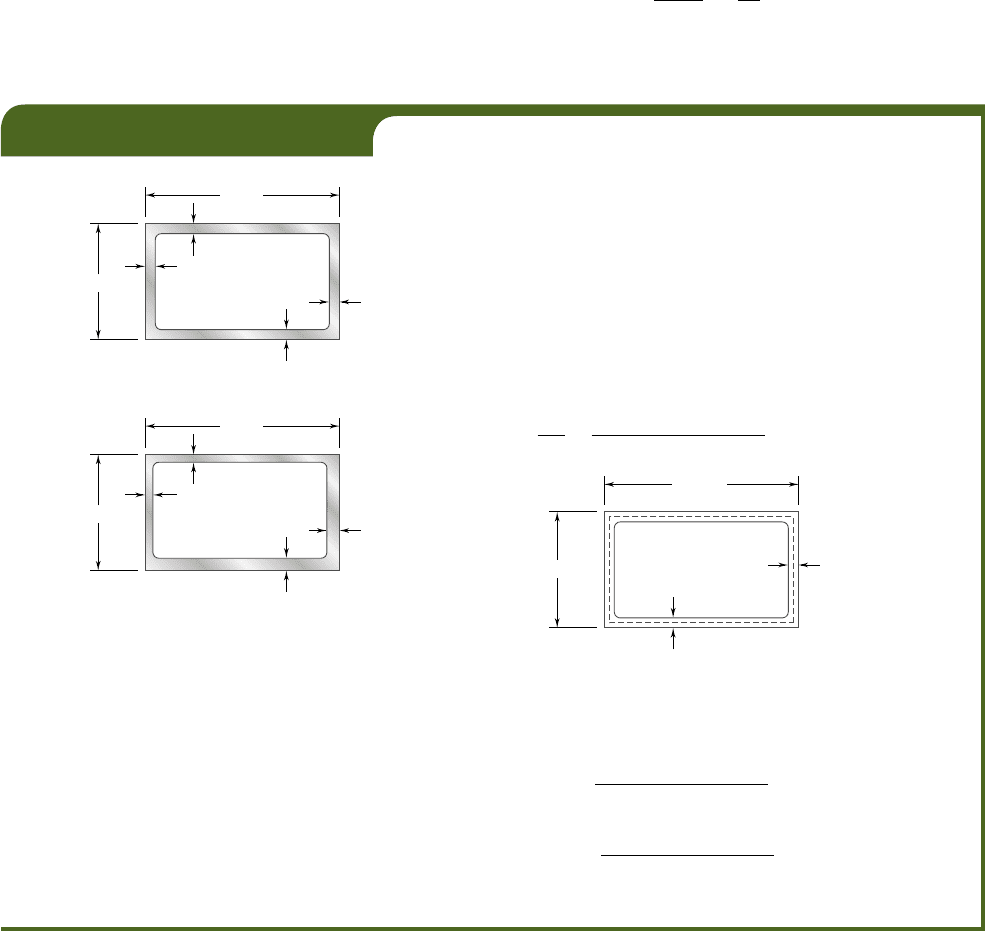
EXAMPLE 3.10

Structural aluminum tubing of 2.5 3 4-in. rectangular cross section was

fabricated by extrusion. Determine the shearing stress in each of the four

walls of a portion of such tubing when it is subjected to a torque of

24 kip ? in., assuming (a) a uniform 0.160-in. wall thickness (Fig. 3.55a),

(b) that, as a result of defective fabrication, walls AB and AC are 0.120-in.

thick, and walls BD and CD are 0.200-in. thick (Fig. 3.55b).

(a) Tubing of Uniform Wall Thickness. The area bounded by

the center line (Fig. 3.56) is

A 5 (3.84 in.)(2.34 in.) 5 8.986 in

Since the thickness of each of the four walls is t 5 0.160 in., we find from

Eq. (3.53) that the shearing stress in each wall is

t 5

2tA

ip ? in.

0.160 in.

8.986 in

5 8.35 ksi

3.84 in.

2.34 in.



0.160 in.



0.160 in.

Fig. 3.56

0.160 in.

4 in.

0.160 in.

0.120 in.

0.200 in.

2.5 in.

(a)

(b)

Fig. 3.55

†See Prob. 11.70.

(b) Tubing with Variable Wall Thickness. Observing that the area

A bounded by the center line is the same as in part a, and substituting

successively t 5 0.120 in. and t 5 0.200 in. into Eq. (3.53), we have

5 t

ip ? in.

0.120 in.

8.986 in

5 11.13 ksi

and

5 t

ip ? in.

0.200 in.

8.986 in

5 6.68 ksi

We note that the stress in a given wall depends only upon its thickness.

bee80288_ch03_140-219.indd Page 202 11/2/10 12:48:33 AM user-f499bee80288_ch03_140-219.indd Page 202 11/2/10 12:48:33 AM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

203

SOLUTION

1. Bar with Square Cross Section. For a solid bar of rectangular

cross section the maximum shearing stress is given by Eq. (3.43)

max

where the coefficient c

is obtained from Table 3.1 in Sec. 3.12. We have

5 0.040 m

5 1.00

208

For t

max

5 t

all

5 40 MPa, we have

max

40 MPa 5

0.208

0.040 m

5 532 N ? m

◀

2. Bar with Rectangular Cross Section. We now have

0.064

5 0.025 m

5 2.56

Interpolating in Table 3.1: c

5 0.259

max

40 MPa 5

0.259

0.064 m

0.025 m

5 414 N ? m

◀

3. Square Tube. For a tube of thickness t, the shearing stress is given

by Eq. (3.53)

t 5

where A is the area bounded by the center line of the cross section. We

have

A 5

0.034 m

5 1.156 3 10

We substitute t 5 t

all

5 40 MPa and t 5 0.006 m and solve for the allow-

able torque:

t 5

40 MPa 5

0.006 m

1.156 3 10

5 555 N ? m

◀

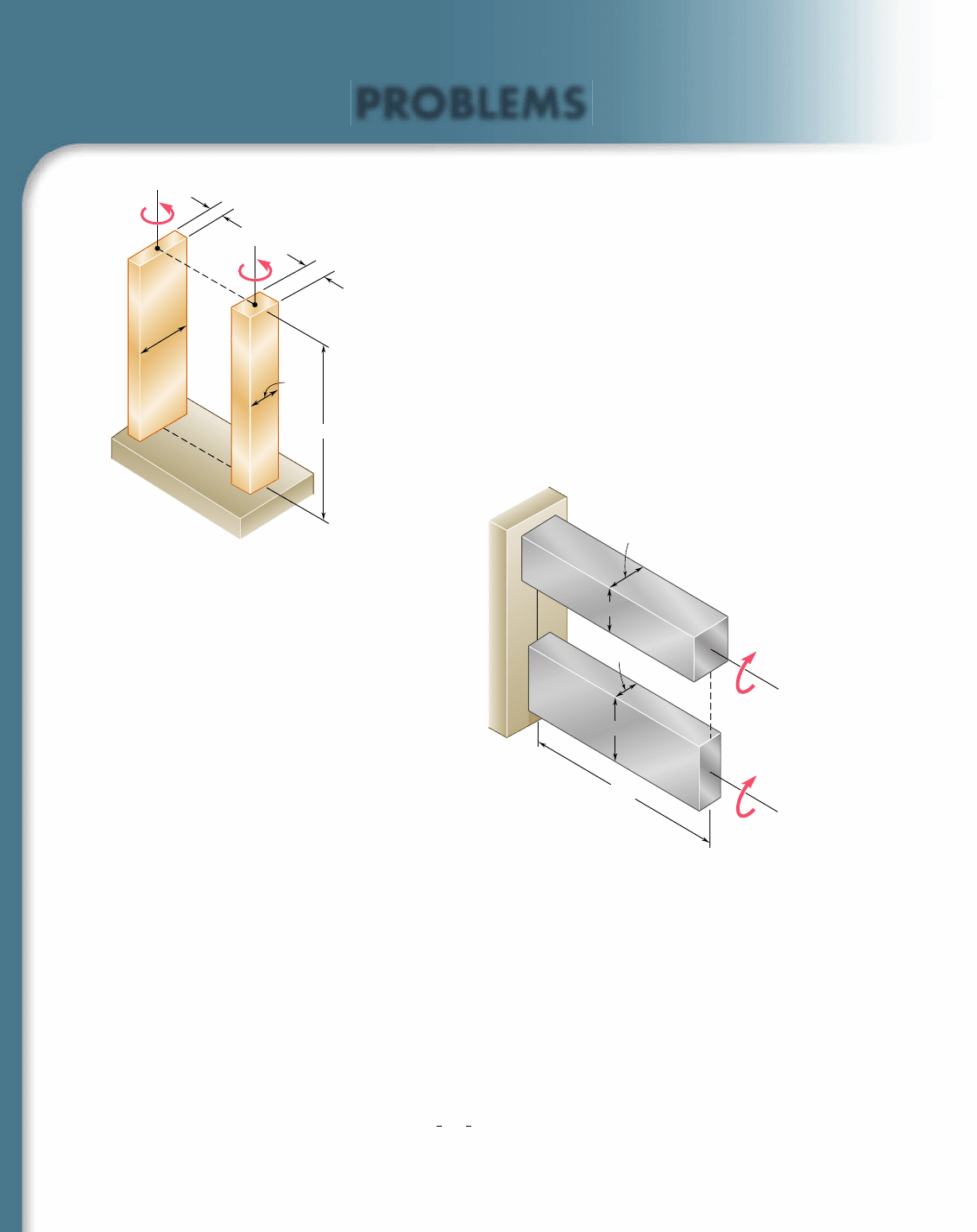
SAMPLE PROBLEM 3.9

Using t

all

5 40 MPa, determine the largest torque that may

be applied to each of the brass bars and to the brass tube

shown. Note that the two solid bars have the same cross-

sectional area, and that the square bar and square tube have

the same outside dimensions.

40 mm

64 mm

25 mm

40 mm

6 mm

(1)

(2)

(3)

34 mm

40 mm

t  6 mm

bee80288_ch03_140-219.indd Page 203 9/21/10 3:09:23 PM user-f499bee80288_ch03_140-219.indd Page 203 9/21/10 3:09:23 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

PROBLEMS

204

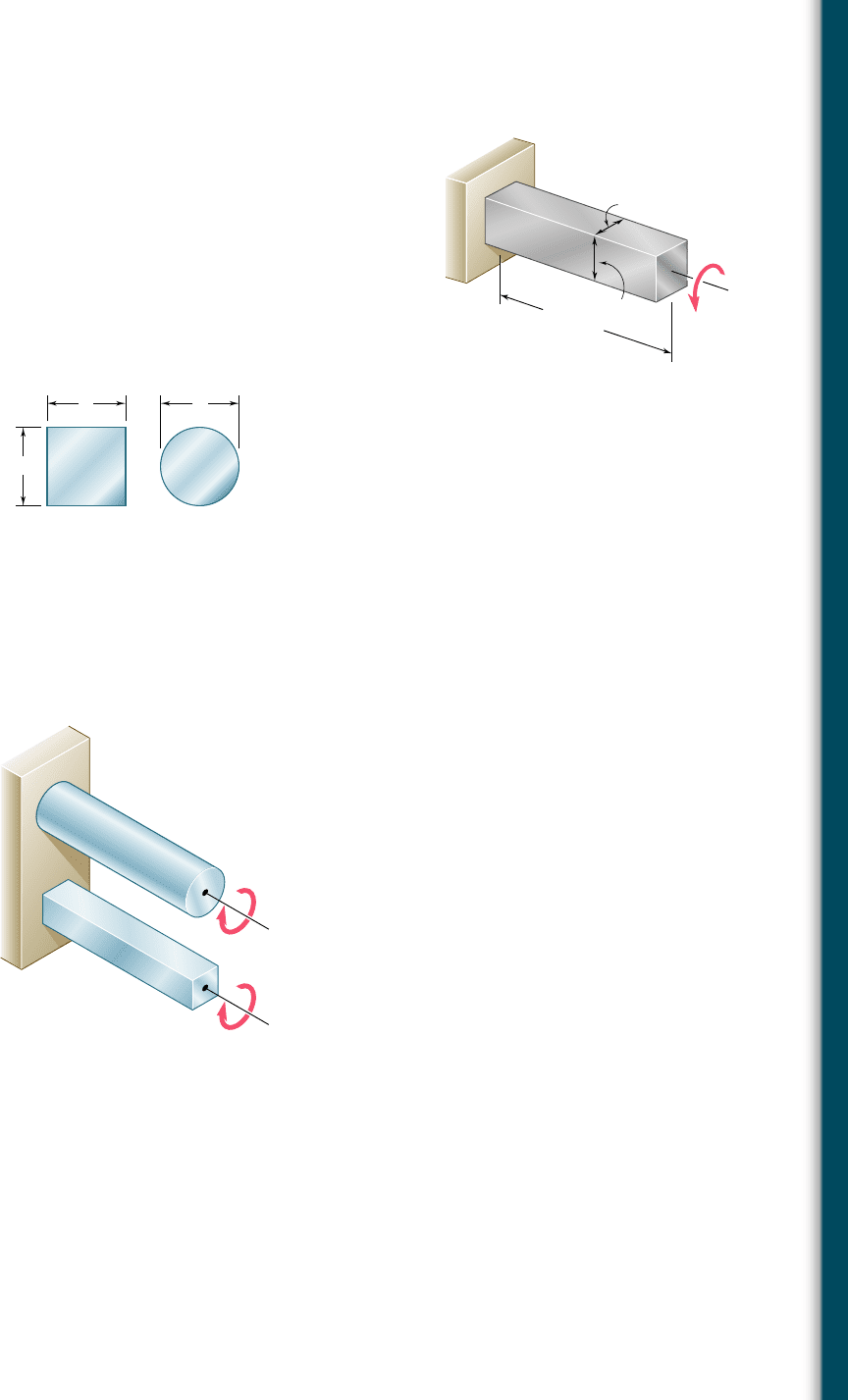
3.121 Determine the largest torque T that can be applied to each of the

two brass bars shown and the corresponding angle of twist at B,

knowing that t

all

5 12 ksi and G 5 5.6 3 10

psi.

3.122 Each of the two brass bars shown is subjected to a torque of mag-

nitude T 5 12.5 kip ? in. Knowing that G 5 5.6 3 10

psi, determine

for each bar the maximum shearing stress and the angle of twist

at B.

3.123 Each of the two aluminum bars shown is subjected to a torque of

magnitude T 5 1800 N ? m. Knowing that G 5 26 GPa, determine

for each bar the maximum shearing stress and the angle of twist

at B.

25 in.

2.4 in.

1.6 in.

1 in.

4 in.

(b)

(a)

Fig. P3.121 and P3.122

3.124 Determine the largest torque T that can be applied to each of the

two aluminum bars shown and the corresponding angle of twist at

B, knowing that t

all

5 50 MPa and G 5 26 GPa.

3.125 Determine the largest allowable square cross section of a steel

shaft of length 20 ft if the maximum shearing stress is not to exceed

10 ksi when the shaft is twisted through one complete revolution.

Use G 5 11.2 3 10

psi.

3.126 Determine the largest allowable length of a stainless steel shaft of

-in. cross section if the shearing stress is not to exceed 15 ksi

when the shaft is twisted through 158. Use G 5 11.2 3 10

psi.

300 mm

38 mm

60 mm

95 mm

(a)

(b)

Fig. P3.123 and P3.124

bee80288_ch03_140-219.indd Page 204 9/21/10 3:09:28 PM user-f499bee80288_ch03_140-219.indd Page 204 9/21/10 3:09:28 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

205

Problems

3.127 The torque T causes a rotation of 28 at end B of the stainless steel

bar shown. Knowing that b 5 20 mm and G 5 75 GPa, determine

the maximum shearing stress in the bar.

3.128 The torque T causes a rotation of 0.68 at end B of the aluminum

bar shown. Knowing that b 5 15 mm and G 5 26 GPa, determine

the maximum shearing stress in the bar.

3.129 Two shafts are made of the same material. The cross section of

shaft A is a square of side b and that of shaft B is a circle of diam-

eter b. Knowing that the shafts are subjected to the same torque,

determine the ratio t

of maximum shearing stresses occurring

in the shafts.

30 mm

750 mm

Fig. P3.127 and P3.128

Fig. P3.129

3.130 Shafts A and B are made of the same material and have the same

cross-sectional area, but A has a circular cross section and B has a

square cross section. Determine the ratio of the maximum shearing

stresses occurring in A and B, respectively, when the two shafts are

subjected to the same torque (T

5 T

). Assume both deformations

to be elastic.

Fig. P3.130, P3.131 and P3.132

3.131 Shafts A and B are made of the same material and have the same

cross-sectional area, but A has a circular cross section and B has a

square cross section. Determine the ratio of the maximum torques

and T

that can be safely applied to A and B, respectively.

3.132 Shafts A and B are made of the same material and have the same

length and cross-sectional area, but A has a circular cross section

and B has a square cross section. Determine the ratio of the maxi-

mum values of the angles f

and f

through which shafts A and

B, respectively, can be twisted.

bee80288_ch03_140-219.indd Page 205 9/21/10 9:17:25 PM user-f499bee80288_ch03_140-219.indd Page 205 9/21/10 9:17:25 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

206

Torsion

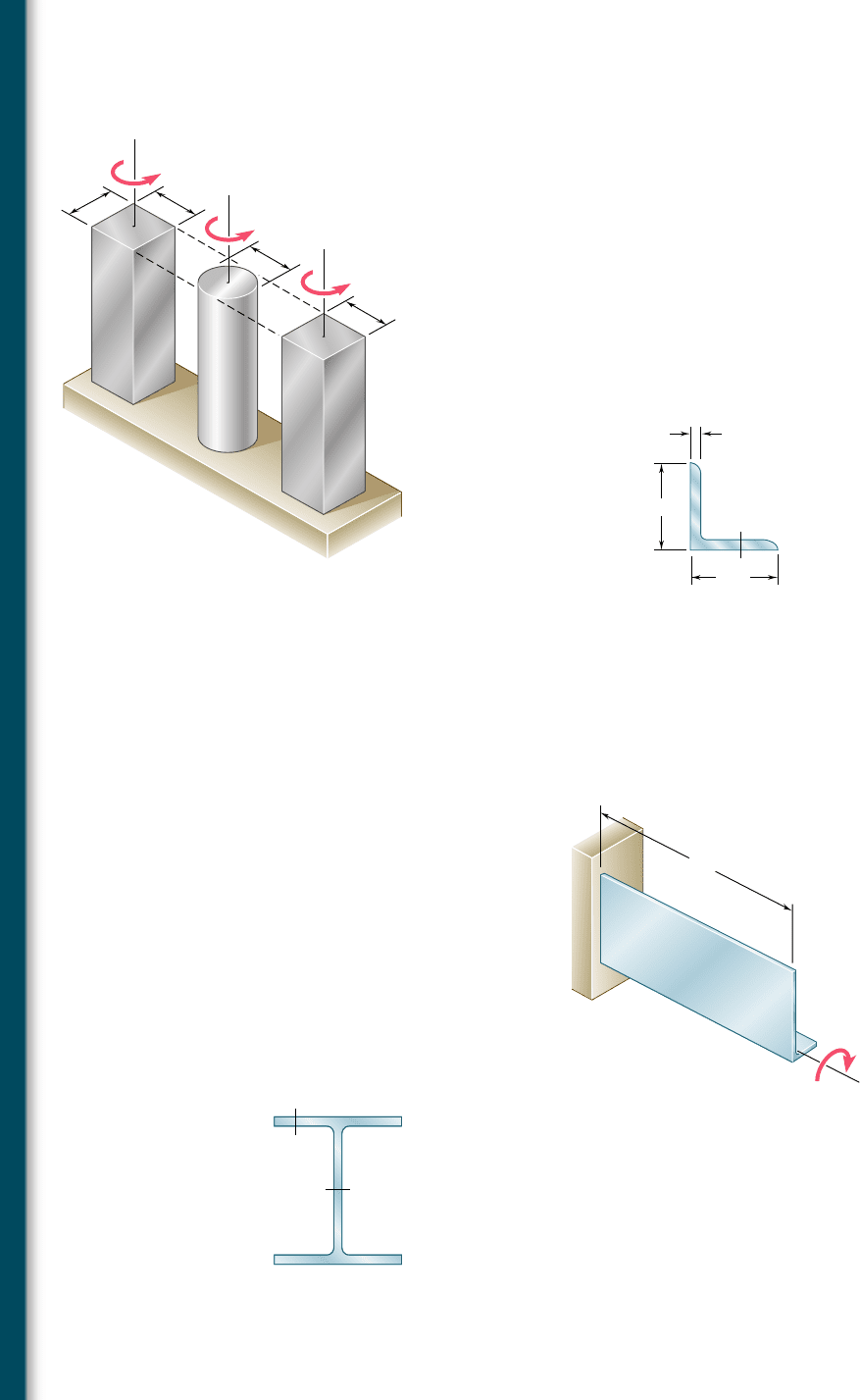
3.133 Each of the three aluminum bars shown is to be twisted through

an angle of 28. Knowing that b 5 30 mm, t

all

5 50 MPa, and G 5

27 GPa, determine the shortest allowable length of each bar.

3.134 Each of the three steel bars is subjected to a torque as shown.

Knowing that the allowable shearing stress is 8 ksi and that b 5

1.4 in., determine the maximum torque T that can be applied to

each bar.

3.135 A 36-kip ? in. torque is applied to a 10-ft-long steel angle with an

L8 3 8 3 1 cross section. From Appendix C we find that the

thickness of the section is 1 in. and that its area is 15 in

. Knowing

that G 5 11.2 3 10

psi, determine (a) the maximum shearing

stress along line a-a, (b) the angle of twist.

(a)

1.2b

(b)

(c)

Fig. P3.133 and P3.134

1 in.

L8  8  1

8 in.

Fig. P3.135

3.136 A 3-m-long steel angle has an L203 3 152 3 12.7 cross section. From

Appendix C we find that the thickness of the section is 12.7 mm and

that its area is 4350 mm

. Knowing that t

all

5 50 MPa and that

G 5 77.2 GPa, and ignoring the effect of stress concentrations, deter-

mine (a) the largest torque T that can be applied, (b) the correspond-

ing angle of twist.

3 m

L203  152  12.7

Fig. P3.136

W8  31

Fig. P3.137

3.137 An 8-ft-long steel member with a W8 3 31 cross section is sub-

jected to a 5-kip ? in. torque. The properties of the rolled-steel

section are given in Appendix C. Knowing that G 5 11.2 3 10

psi,

determine (a) the maximum shearing stress along line a-a, (b) the

maximum shearing stress along line b-b, (c) the angle of twist. (Hint:

consider the web and flanges separately and obtain a relation

between the torques exerted on the web and a flange, respectively,

by expressing that the resulting angles of twist are equal.)

bee80288_ch03_140-219.indd Page 206 9/21/10 3:09:38 PM user-f499bee80288_ch03_140-219.indd Page 206 9/21/10 3:09:38 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03