Beer F.P., Johnston E.R., DeWolf J.T., Mazurek D.F. Mechanics of Materials

Подождите немного. Документ загружается.

Apago PDF Enhancer

207

Problems

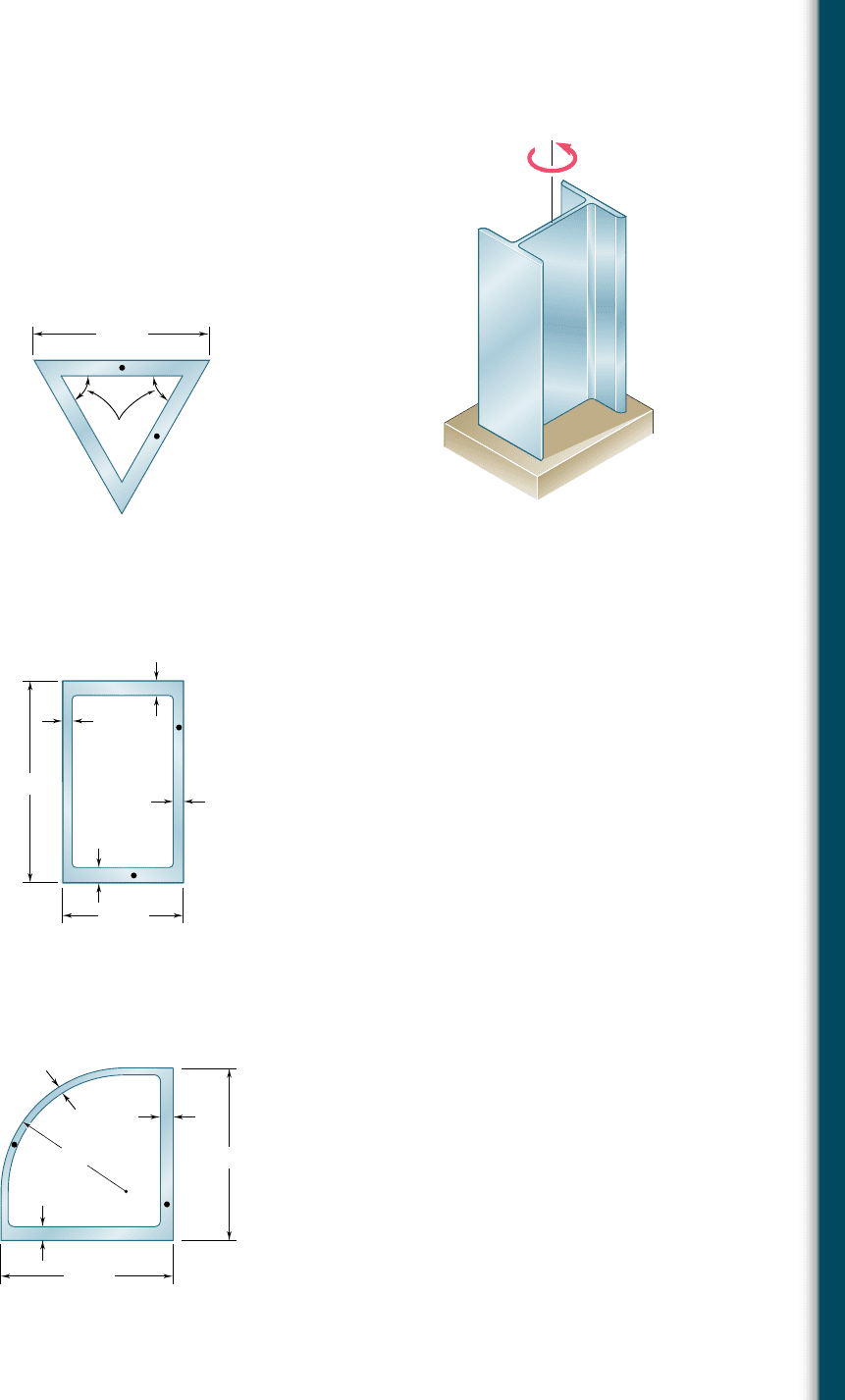
3.138 A 4-m-long steel member has a W310 3 60 cross section. Knowing

that G 5 77.2 GPa and that the allowable shearing stress is 40 MPa,

determine (a) the largest torque T that can be applied, (b) the cor-

responding angle of twist. Refer to Appendix C for the dimensions

of the cross section and neglect the effect of stress concentrations.

(See hint of Prob. 3.137.)

3.139 A torque T 5 750 kN ? m is applied to the hollow shaft shown that

has a uniform 8-mm wall thickness. Neglecting the effect of stress

concentrations, determine the shearing stress at points a and b.

310  60

Fig. P3.138

90 mm

60

Fig. P3.139

3.140 A torque T 5 5 kN ? m is applied to a hollow shaft having the

cross section shown. Neglecting the effect of stress concentrations,

determine the shearing stress at points a and b.

125 mm

6 mm

10 mm

75 mm

10 mm

6 mm

Fig. P3.140

40 mm

2 mm

4 mm

55 mm

Fig. P3.141

3.141 A 90-N ? m torque is applied to a hollow shaft having the cross

section shown. Neglecting the effect of stress concentrations,

determine the shearing stress at points a and b.

bee80288_ch03_140-219.indd Page 207 9/21/10 3:09:47 PM user-f499bee80288_ch03_140-219.indd Page 207 9/21/10 3:09:47 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

208

Torsion

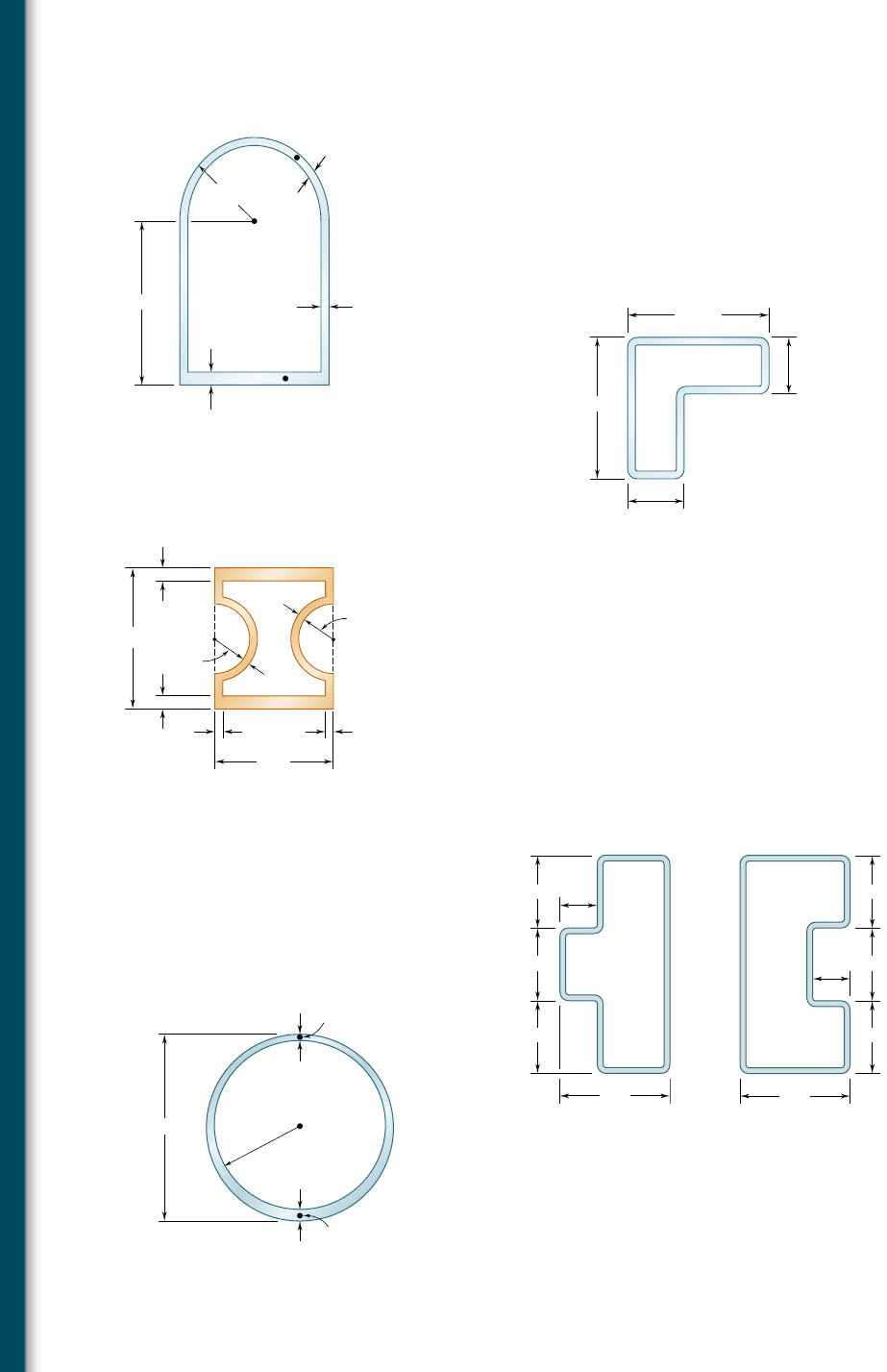
3.142 A 5.6 kN ? m-torque is applied to a hollow shaft having the cross

section shown. Neglecting the effect of stress concentrations,

determine the shearing stress at points a and b.

3.143 A hollow member having the cross section shown is formed from

sheet metal of 2-mm thickness. Knowing that the shearing stress

must not exceed 3 MPa, determine the largest torque that can be

applied to the member.

100 mm

8 mm

5 mm

50 mm

Fig. P3.142

20 mm

50 mm

Fig. P3.143

3.144 A hollow brass shaft has the cross section shown. Knowing that the

shearing stress must not exceed 12 ksi and neglecting the effect of

stress concentrations, determine the largest torque that can be

applied to the shaft.

3.145 and 3.146 A hollow member having the cross section shown

is to be formed from sheet metal of 0.06-in. thickness. Knowing

that a 1250 lb ? in.-torque will be applied to the member, deter-

mine the smallest dimension d that can be used if the shearing

stress is not to exceed 750 psi.

0.5 in.

5 in.

0.2 in.

0.5 in.

6 in.

1.5 in.

Fig. P3.144

2 in.

3 in.

Fig. P3.145

2 in.

3 in.

Fig. P3.146

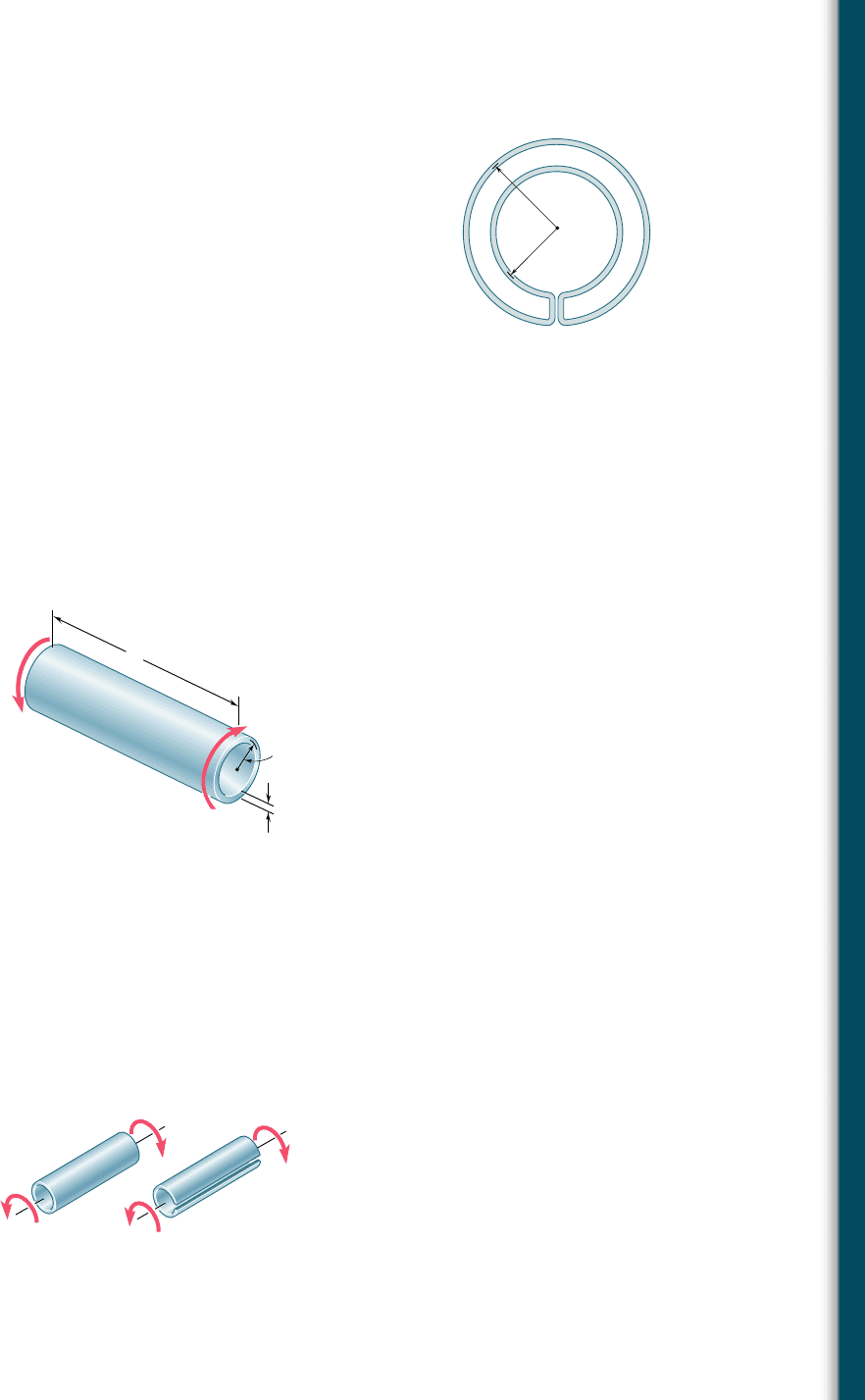
3.147 A hollow cylindrical shaft was designed to have a uniform wall

thickness of 0.1 in. Defective fabrication, however, resulted in the

shaft having the cross section shown. Knowing that a 15 kip ? in.-

torque is applied to the shaft, determine the shearing stresses at

points a and b.

1.1 in.

0.12 in.

0.08 in.

2.4 in.

Fig. P3.147

bee80288_ch03_140-219.indd Page 208 9/21/10 3:09:56 PM user-f499bee80288_ch03_140-219.indd Page 208 9/21/10 3:09:56 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

209

Problems

3.148 A cooling tube having the cross section shown is formed from a

sheet of stainless steel of 3-mm thickness. The radii c

5 150 mm

and c

5 100 mm are measured to the center line of the sheet

metal. Knowing that a torque of magnitude T 5 3 kN ? m is applied

to the tube, determine (a) the maximum shearing stress in the

tube, (b) the magnitude of the torque carried by the outer circular

shell. Neglect the dimension of the small opening where the outer

and inner shells are connected.

3.149 A hollow cylindrical shaft of length L, mean radius c

, and uni-

form thickness t is subjected to a torque of magnitude T. Con-

sider, on the one hand, the values of the average shearing stress

ave

and the angle of twist f obtained from the elastic torsion

formulas developed in Secs. 3.4 and 3.5 and, on the other hand,

the corresponding values obtained from the formulas developed

in Sec. 3.13 for thin-walled shafts. (a) Show that the relative error

introduced by using the thin-walled-shaft formulas rather than the

elastic torsion formulas is the same for t

ave

and f and that the rela-

tive error is positive and proportional to the ratio tyc

. (b) Compare

the percent error corresponding to values of the ratio tyc

of 0.1,

0.2, and 0.4.

Fig. P3.148

Fig. P3.149

3.150 Equal torques are applied to thin-walled tubes of the same length

L, same thickness t, and same radius c. One of the tubes has been

slit lengthwise as shown. Determine (a) the ratio t

of the maxi-

mum shearing stresses in the tubes, (b) the ratio f

of the

angles of twist of the tubes.

(a)

(b)

Fig. P3.150

bee80288_ch03_140-219.indd Page 209 9/21/10 3:10:06 PM user-f499bee80288_ch03_140-219.indd Page 209 9/21/10 3:10:06 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

210

REVIEW AND SUMMARY

This chapter was devoted to the analysis and design of shafts sub-

jected to twisting couples, or torques. Except for the last two sections

of the chapter, our discussion was limited to circular shafts.

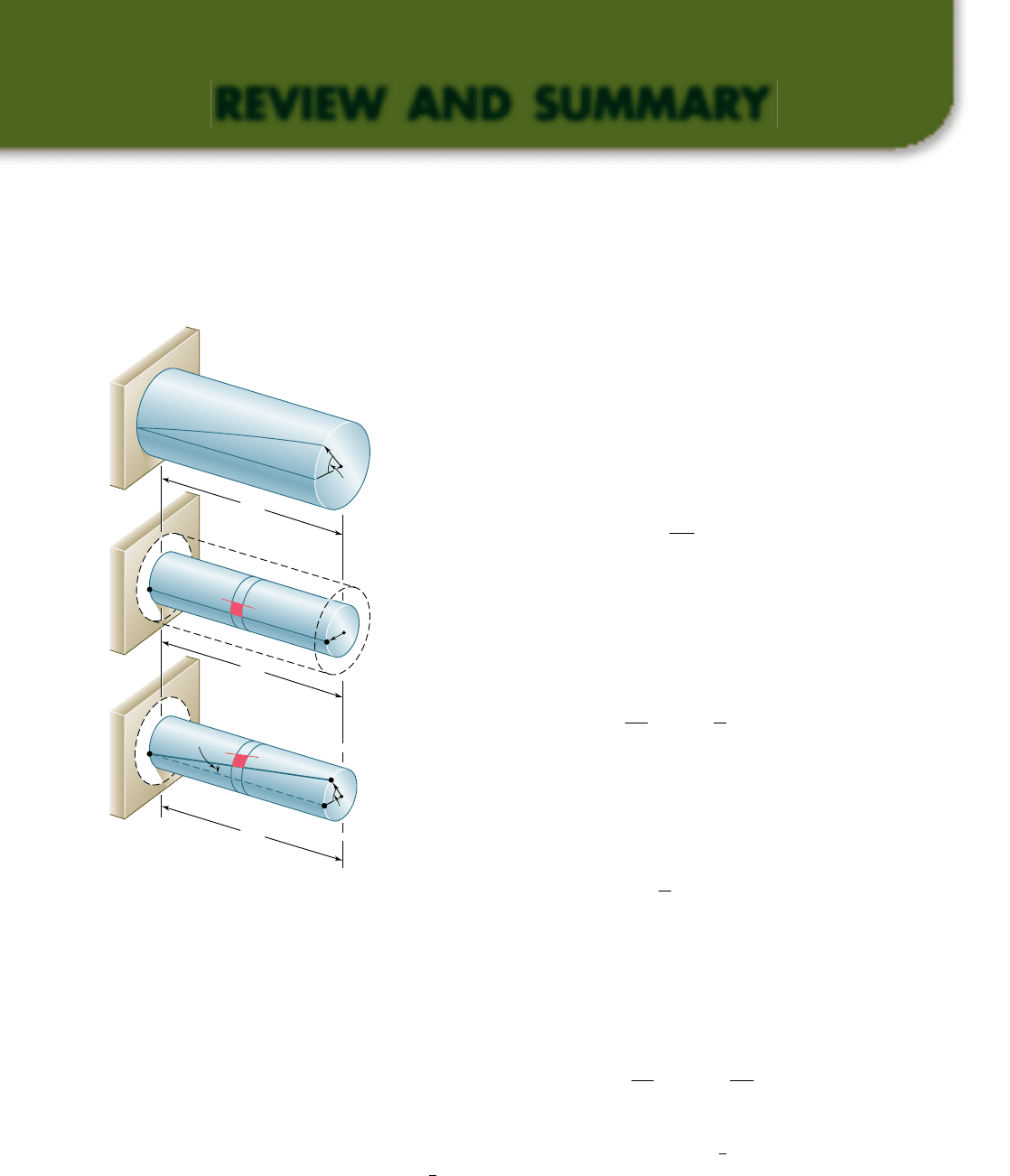
In a preliminary discussion [Sec. 3.2], it was pointed out that

the distribution of stresses in the cross section of a circular shaft is

statically indeterminate. The determination of these stresses, there-

fore, requires a prior analysis of the deformations occurring in the

shaft [Sec. 3.3]. Having demonstrated that in a circular shaft sub-

jected to torsion, every cross section remains plane and undistorted,

we derived the following expression for the shearing strain in a small

element with sides parallel and perpendicular to the axis of the shaft

and at a distance r from that axis:

g 5

(3.2)

where f is the angle of twist for a length L of the shaft (Fig. 3.57).

Equation (3.2) shows that the shearing strain in a circular shaft var-

ies linearly with the distance from the axis of the shaft. It follows

that the strain is maximum at the surface of the shaft, where r is

equal to the radius c of the shaft. We wrote

max

g 5

 g

(3.3, 4)

Considering shearing stresses in a circular shaft within the elastic

range [Sec. 3.4] and recalling Hooke’s law for shearing stress and

strain, t 5 Gg, we derived the relation

t 5

 t

(3.6)

which shows that within the elastic range, the shearing stress t in a

circular shaft also varies linearly with the distance from the axis of

the shaft. Equating the sum of the moments of the elementary forces

exerted on any section of the shaft to the magnitude T of the torque

applied to the shaft, we derived the elastic torsion formulas

max

t 5

(3.9, 10)

where c is the radius of the cross section and J its centroidal polar

moment of inertia. We noted that

J 5

for a solid shaft and

J 5

p1c

2 c

2 for a hollow shaft of inner radius c

and outer

radius c

Deformations in circular shafts

(a)

(b)

(c)









Fig. 3.57

Shearing stresses in elastic range

bee80288_ch03_140-219.indd Page 210 9/21/10 3:10:12 PM user-f499bee80288_ch03_140-219.indd Page 210 9/21/10 3:10:12 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

211

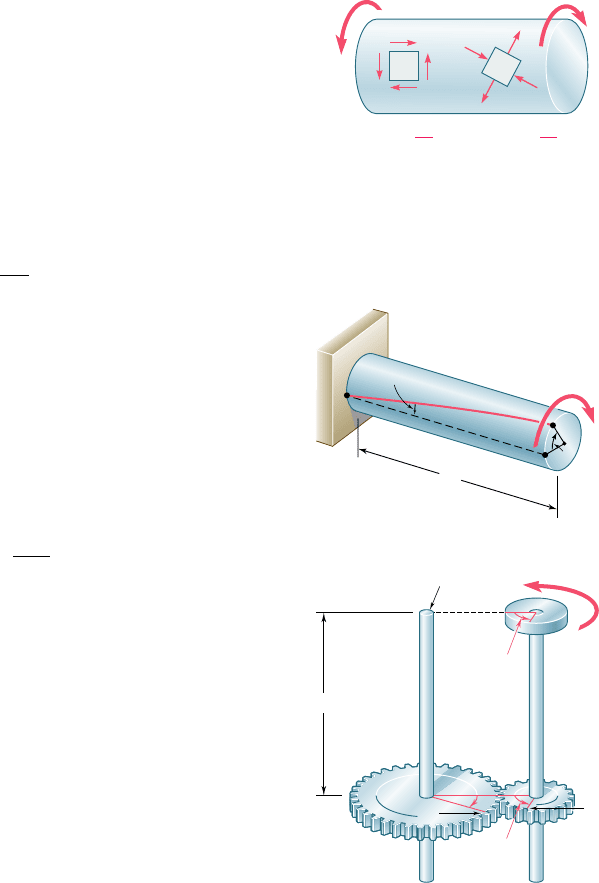
We noted that while the element a in Fig. 3.58 is in pure shear,

the element c in the same figure is subjected to normal stresses of

the same magnitude, TcyJ, two of the normal stresses being tensile

and two compressive. This explains why in a torsion test ductile

materials, which generally fail in shear, will break along a plane per-

pendicular to the axis of the specimen, while brittle materials, which

are weaker in tension than in shear, will break along surfaces forming

a 458 angle with that axis.

In Sec. 3.5, we found that within the elastic range, the angle of twist

f of a circular shaft is proportional to the torque T applied to it (Fig.

3.59). Expressing f in radians, we wrote

f 5

(3.16)

where L 5 length of shaft

J 5 polar moment of inertia of cross section

G 5 modulus of rigidity of material

If the shaft is subjected to torques at locations other than its ends

or consists of several parts of various cross sections and possibly of

different materials, the angle of twist of the shaft must be expressed

as the algebraic sum of the angles of twist of its component parts

[Sample Prob. 3.3]:

f 5

(3.17)

We observed that when both ends of a shaft BE rotate (Fig. 3.60),

the angle of twist of the shaft is equal to the difference between the

angles of rotation f

and f

of its ends. We also noted that when

two shafts AD and BE are connected by gears A and B, the torques

applied, respectively, by gear A on shaft AD and by gear B on shaft

BE are directly proportional to the radii r

and r

of the two gears—

since the forces applied on each other by the gear teeth at C are

equal and opposite. On the other hand, the angles f

and f

through

which the two gears rotate are inversely proportional to r

and r

—

since the arcs CC9 and CC0 described by the gear teeth are equal

[Example 3.04 and Sample Prob. 3.4].

If the reactions at the supports of a shaft or the internal torques

cannot be determined from statics alone, the shaft is said to be stati-

cally indeterminate [Sec. 3.6]. The equilibrium equations obtained

from free-body diagrams must then be complemented by relations

involving the deformations of the shaft and obtained from the geom-

etry of the problem [Example 3.05, Sample Prob. 3.5].

In Sec. 3.7, we discussed the design of transmission shafts. We first

observed that the power P transmitted by a shaft is

P 5 2p fT (3.20)

where T is the torque exerted at each end of the shaft and f the fre-

quency or speed of rotation of the shaft. The unit of frequency is

Review and Summary

Angle of twist

Statically indeterminate shafts

Fig. 3.59





max



Fixed end



Fig. 3.60



max





45



Fig. 3.58

Transmission shafts

bee80288_ch03_140-219.indd Page 211 9/21/10 3:10:21 PM user-f499bee80288_ch03_140-219.indd Page 211 9/21/10 3:10:21 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

212

Torsion

the revolution per second (s

) or hertz (Hz). If SI units are used,

T is expressed in newton-meters (N ? m) and P in watts (W). If U.S.

customary units are used, T is expressed in lb ? ft or lb ? in., and P

in ft ? lb/s or in ? lb/s; the power may then be converted into horse-

power (hp) through the use of the relation

1 hp 5 550 ft ? lb/s 5 6600 in ? lb/s

To design a shaft to transmit a given power P at a frequency f, you

should first solve Eq. (3.20) for T. Carrying this value and the maxi-

mum allowable value of t for the material used into the elastic for-

mula (3.9), you will obtain the corresponding value of the parameter

Jyc, from which the required diameter of the shaft may be calculated

[Examples 3.06 and 3.07].

In Sec. 3.8, we discussed stress concentrations in circular shafts.

We saw that the stress concentrations resulting from an abrupt

change in the diameter of a shaft can be reduced through the use

of a fillet (Fig. 3.61). The maximum value of the shearing stress at

the fillet is

max

5 K

(3.25)

where the stress TcyJ is computed for the smaller-diameter shaft, and

where K is a stress-concentration factor. Values of K were plotted in

Fig. 3.29 on p. 179 against the ratio ryd, where r is the radius of the

fillet, for various values of Dyd.

Sections 3.9 through 3.11 were devoted to the discussion of plastic

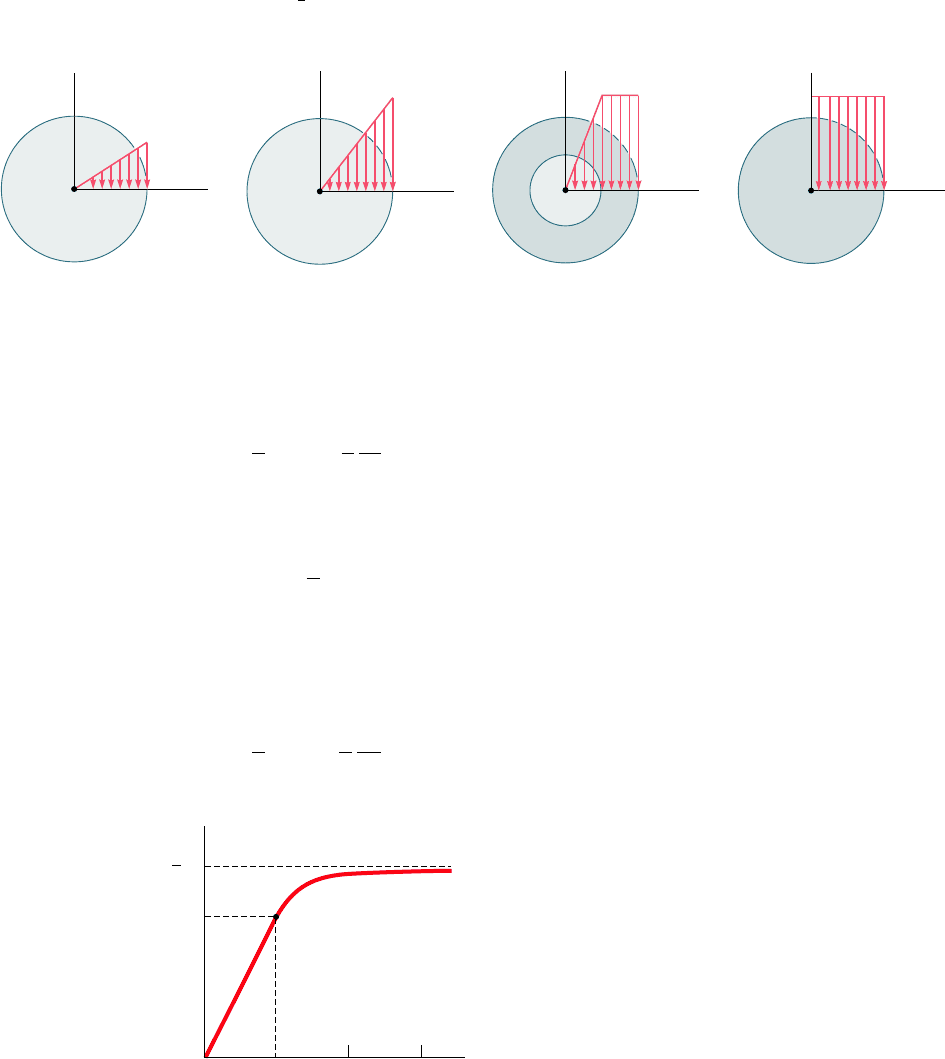
deformations and residual stresses in circular shafts. We first recalled

that even when Hooke’s law does not apply, the distribution of strains

in a circular shaft is always linear [Sec. 3.9]. If the shearing-stress-

strain diagram for the material is known, it is then possible to plot

the shearing stress t against the distance r from the axis of the shaft

for any given value of t

max

(Fig. 3.62). Summing the contributions to

the torque of annular elements of radius r and thickness dr , we

expressed the torque T as

T 5

rt12pr dr25 2p

t dr

(3.26)

where t is the function of r plotted in Fig. 3.62.

An important value of the torque is the ultimate torque T

which

causes failure of the shaft. This value can be determined, either

experimentally, or by carrying out the computations indicated

above with t

max

chosen equal to the ultimate shearing stress t

the material. From T

, and assuming a linear stress distribution

(Fig 3.63), we determined the corresponding fictitious stress R

cyJ, known as the modulus of rupture in torsion of the given

material.

Considering the idealized case of a solid circular shaft made of

an elastoplastic material [Sec. 3.10], we first noted that, as long as

Stress concentrations

Fig. 3.61

Plastic deformations

␶

␳

max

␶

Fig. 3.62

␳

␶

Fig. 3.63

Modulus of rupture

bee80288_ch03_140-219.indd Page 212 11/2/10 9:56:48 PM user-f494bee80288_ch03_140-219.indd Page 212 11/2/10 9:56:48 PM user-f494 /207/BSMB003/work%0/indd%0/207/BSMB003/work%0/indd%0

Apago PDF Enhancer

213

max

does not exceed the yield strength t

of the material, the stress

distribution across a section of the shaft is linear (Fig. 3.64a). The

torque T

corresponding to t

max

5 t

(Fig. 3.64b) is known as the

maximum elastic torque; for a solid circular shaft of radius c, we

have

(3.29)

Review and Summary

(a)







max





(b)







max





(c)









(d)







Fig. 3.64

As the torque increases, a plastic region develops in the shaft around

an elastic core of radius r

. The torque T corresponding to a given

value of r

was found to be

T 5

1 2

(3.32)

We noted that as r

approaches zero, the torque approaches a limit-

ing value T

, called the plastic torque of the shaft considered:

(3.33)

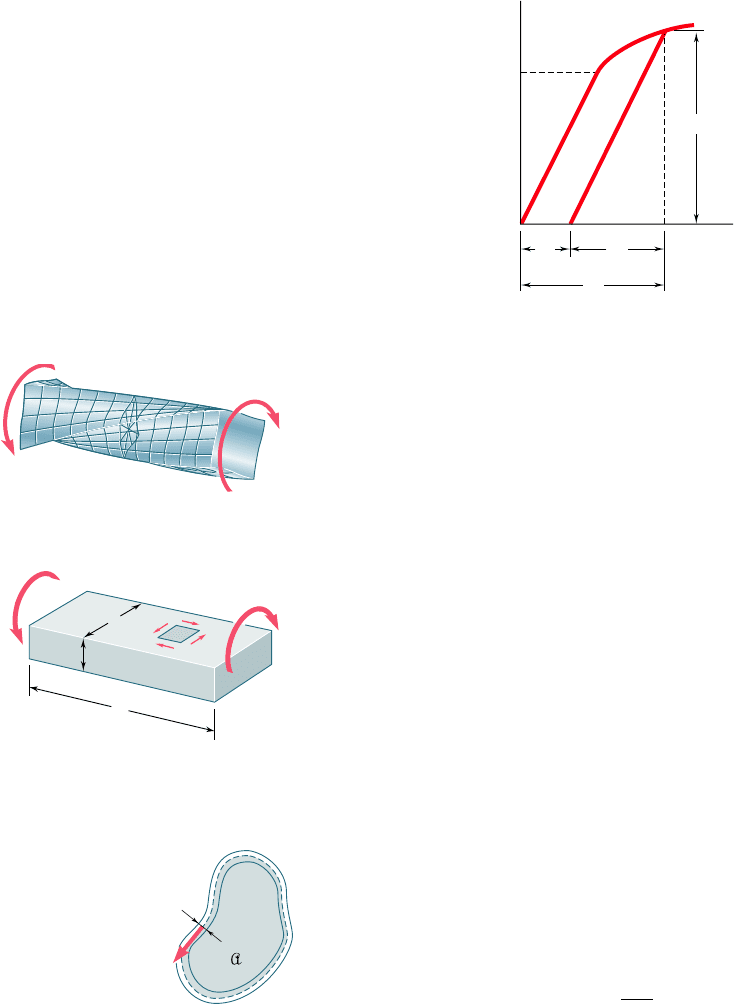
Plotting the torque T against the angle of twist f of a solid

circular shaft (Fig. 3.65), we obtained the segment of straight line

0Y defined by Eq. (3.16), followed by a curve approaching the

straight line T 5 T

and defined by the equation

T 5

a1 2

(3.37)





Fig. 3.65

Solid shaft of elastoplastic material

bee80288_ch03_140-219.indd Page 213 9/21/10 3:10:34 PM user-f499bee80288_ch03_140-219.indd Page 213 9/21/10 3:10:34 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

214

Torsion

Loading a circular shaft beyond the onset of yield and unloading it

[Sec. 3.11] results in a permanent deformation characterized by the

angle of twist f

5 f 2 f9, where f corresponds to the loading

phase described in the previous paragraph, and f9 to the unloading

phase represented by a straight line in Fig. 3.66. There will also be

residual stresses in the shaft, which can be determined by adding the

maximum stresses reached during the loading phase and the reverse

stresses corresponding to the unloading phase [Example 3.09].

Permanent deformation.

Residual stresses





Fig. 3.66

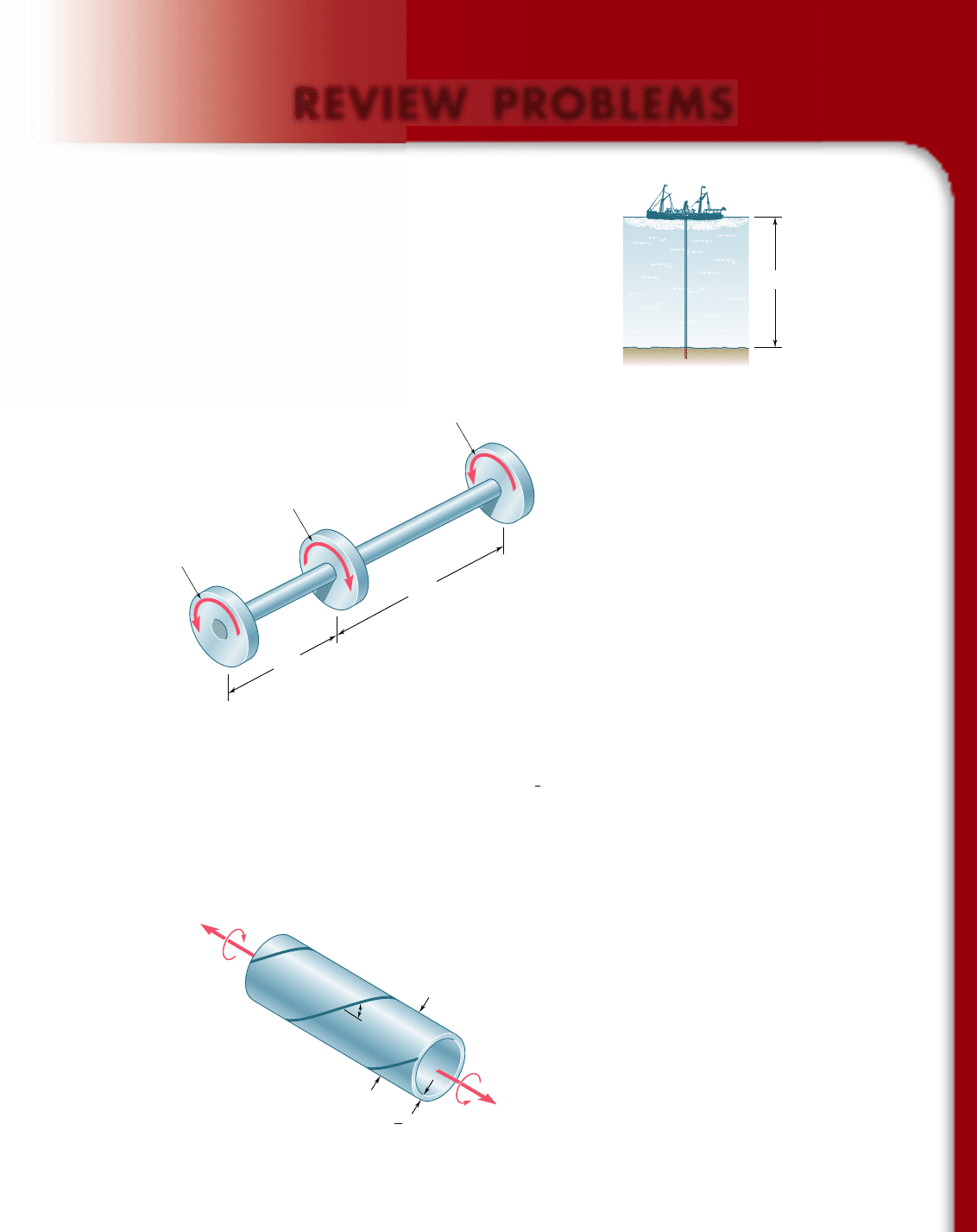
The last two sections of the chapter dealt with the torsion of noncir-

cular members. We first recalled that the derivation of the formulas

for the distribution of strain and stress in circular shafts was based on

the fact that due to the axisymmetry of these members, cross sections

remain plane and undistorted. Since this property does not hold for

noncircular members, such as the square bar of Fig. 3.67, none of the

formulas derived earlier can be used in their analysis [Sec. 3.12].

It was indicated in Sec. 3.12 that in the case of straight bars with a

uniform rectangular cross section (Fig. 3.68), the maximum shearing

stress occurs along the center line of the wider face of the bar. For-

mulas for the maximum shearing stress and the angle of twist were

given without proof. The membrane analogy for visualizing the dis-

tribution of stresses in a noncircular member was also discussed.

We next analyzed the distribution of stresses in noncircular thin-walled

hollow shafts [Sec. 3.13]. We saw that the shearing stress is parallel to

the wall surface and varies both across the wall and along the wall cross

section. Denoting by t the average value of the shearing stress computed

across the wall at a given point of the cross section, and by t the thick-

ness of the wall at that point (Fig. 3.69), we showed that the product

q 5 tt, called the shear flow, is constant along the cross section.

Furthermore, denoting by T the torque applied to the hollow

shaft and by A the area bounded by the center line of the wall cross

section, we expressed as follows the average shearing stress t at any

given point of the cross section:

t 5

(3.53)

Torsion of noncircular members

Fig. 3.67

Bars of rectangular cross section

max



Fig. 3.68

Thin-walled hollow shafts



Fig. 3.69

bee80288_ch03_140-219.indd Page 214 9/21/10 3:10:39 PM user-f499bee80288_ch03_140-219.indd Page 214 9/21/10 3:10:39 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

215

REVIEW PROBLEMS

3.151 The ship at A has just started to drill for oil on the ocean floor

at a depth of 5000 ft. Knowing that the top of the 8-in.-diameter

steel drill pipe (G 5 11.2 3 10

psi) rotates through two complete

revolutions before the drill bit at B starts to operate, determine

the maximum shearing stress caused in the pipe by torsion.

3.152 The shafts of the pulley assembly shown are to be designed. Knowing

that the allowable shearing stress in each shaft is 8.5 ksi, determine

the smallest allowable diameter of (a) shaft AB, (b) shaft BC.

5000 ft

Fig. P3.151

6.8 kip · in.

72 in.

10.4 kip · in.

3.6 kip · in.

48 in.

Fig. P3.152

3.153 A steel pipe of 12-in. outer diameter is fabricated from

-in.-thick

plate by welding along a helix that forms an angle of 458 with a

plane perpendicular to the axis of the pipe. Knowing that the

maximum allowable tensile stress in the weld is 12 ksi, determine

the largest torque that can be applied to the pipe.

12 in.

in.

45⬚

Fig. P3.153

bee80288_ch03_140-219.indd Page 215 9/21/10 3:11:46 PM user-f499bee80288_ch03_140-219.indd Page 215 9/21/10 3:11:46 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03

Apago PDF Enhancer

216

Torsion

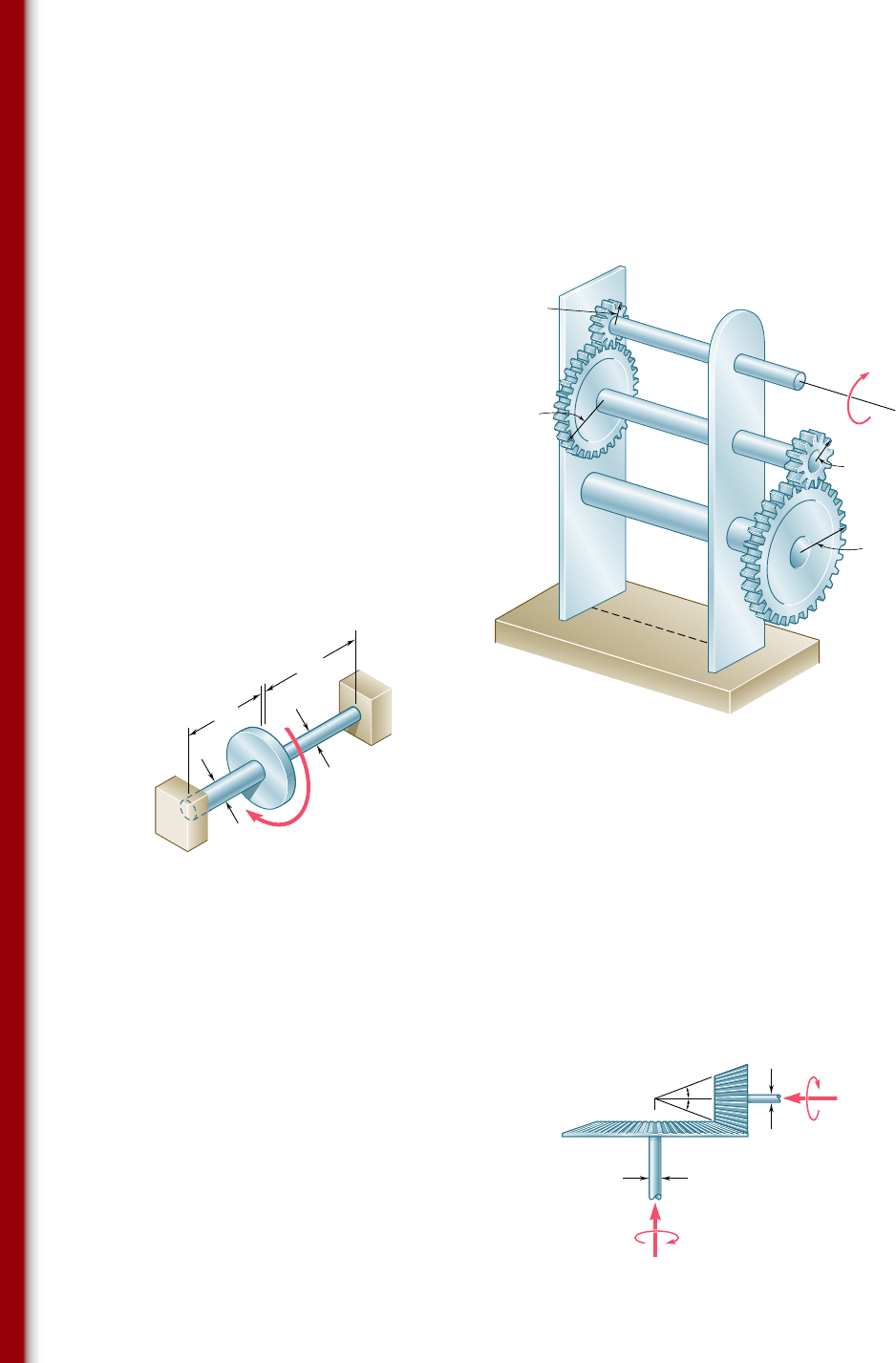
3.154 For the gear train shown, the diameters of the three solid shafts

are:

5 20 mm d

5 25 mm d

5 40 mm

Knowing that for each shaft the allowable shearing stress is 60 MPa,

determine the largest torque T that can be applied.

3.155 Two solid steel shafts (G 5 77.2 GPa) are connected to a cou-

pling disk B and to fixed supports at A and C. For the loading

shown, determine (a) the reaction at each support, (b) the maxi-

mum shearing stress in shaft AB, (c) the maximum shearing stress

in shaft BC.

3.156 In the bevel-gear system shown, a 5 18.438. Knowing that the

allowable shearing stress is 8 ksi in each shaft and that the system

is in equilibrium, determine the largest torque T

that can be

applied at A.

75 mm

30 mm

90 mm

30 mm

Fig. P3.154

250 mm

38 mm

1.4 kN · m

50 mm

200 mm

Fig. P3.155

␣

0.625 in.

0.5 in.

Fig. P3.156

bee80288_ch03_140-219.indd Page 216 9/21/10 3:12:38 PM user-f499bee80288_ch03_140-219.indd Page 216 9/21/10 3:12:38 PM user-f499 /Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03/Users/user-f499/Desktop/Temp Work/Don't Delete Job/MHDQ251:Beer:201/ch03