Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

170 3. Nuclear reactions

ndz

ψ=

ikz

(1+

2πif(0)

ndz)

ikz

ψ=

Fig. 3.28. A plane wave, ψ =exp(ikz) is incident from the left on a thin slice of

material of thickness dz containing a density n of scatterers. Beyond the slice, the

wave is the sum of the incident wave and the scattered waves from all scatterers

in the slice. As shown in the text, the wavefunction takes the form of Equation

(3.222).

ψ(z>0) = exp(ikz)



nf(0)dz



dy exp



ik(x

+ y

)



(3.221)

Using



∞

du =

√

2πe

−iπ/4

, we ﬁnd

ψ(z>0) = exp(ikz)



2πif(θ =0)

ndz



(3.222)

The magnitude of ψ is

|ψ(z>0)|

=1−

4πIm(f(0))

ndz. (3.223)

The total cross-section is deﬁned by the probability dP = σ

tot

ndz so we

deduce the so-called optical theorem:

tot

4πIm(f(0))

. (3.224)

Exercises for Chapter 3 171

The eﬀect of the real part of f can be seen by writing the wavefunction

(3.222) just after the slice:

ψ(dz)=



1 −

2πIm(f(0))



exp





2πnRef(0)





.(3.225)

This implies that the index of refraction is

index of refraction = 1 +

nRe(f(0))

2π

, (3.226)

where λ =2π/k is the neutron wavelength. Note that for solids n ∼ a

−3

so, if f ∼ fm then the index diﬀers signiﬁcantly from unity for λ ∼ 100a

corresponding to neutrons with E ∼ 10

−5

eV.

The fact that low-energy neutron refraction index is signiﬁcantly diﬀer-

ent from unity is due to the fact that the scattering amplitude on nuclei

approaches a constant for k → 0. This is unlike the case of photons where

theamplitudeapproacheszerofork → 0 and, consequently, the refraction

index approaches a constant, often near unity.

The neutron refraction index can be suﬃciently important to permit the

construction of neutron guides that use total internal reﬂection. At suﬃciently

low energies, it is even possible to construct neutron containers that total

reﬂect neutrons of all scattering angles. While this may seem surprising, it is

just equivalent to the mean kinetic energy of the neutrons being less than its

mean potential energy within the wall of the container.

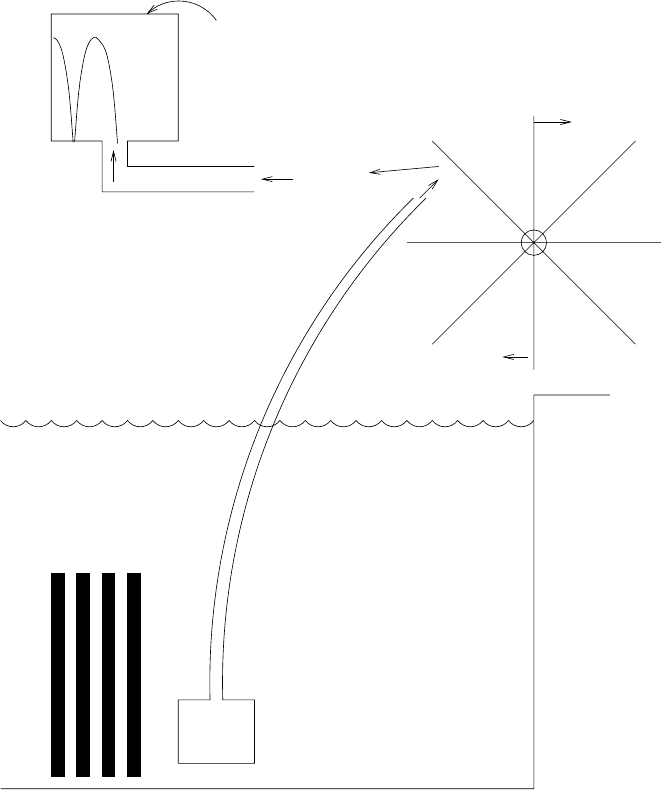
Figure 3.29 gives a example of how neutrons can be captured and then

stored for study. We will see in Chap. 4 how such stored neutrons can be

used to measure the neutron lifetime.

3.8 Bibliography

1. Collision Theory M. L. Goldberger and K. M. Watson, John Wiley &

Sons, 1964

2. Electron Scattering and Nuclear and Nucleon structure, R. Hofstadter,

W.A. Benjamin, New-York (1963)

Exercises

3.1 Using the data in Fig. 3.4 and neglecting scattering on oxygen, calculate

the mean free path of thermal neutrons (p

/2m ∼ kT) in normal water and

in heavy water (where the

H is replaced with

H. On average, how many

elastic collisions will the neutron suﬀer before being absorbed by the (n, γ)

reaction? How much time will this typically take?

172 3. Nuclear reactions

turbine

gravitational trap

absorber

neutron guide

20K

300K

fuel elements

Uranium

Fig. 3.29. A schematic of the system at the Institute Laue-Langevin for producing

ultra-cold neutrons [35]. Neutrons produced by Uranium ﬁssion diﬀuse into the

water moderator where they are thermalized to a temperature of ∼ 300 K by elastic

scattering on the protons in water molecules. Some of the neutrons diﬀuse into a

cold deuterium ﬂask where they are further thermalized to ∼ 20 K. (Deuterium is

used because of its low radiative capture cross-section; see Fig. 3.4.) Neutrons then

escape from the reactor through a neutron guide that uses total internal reﬂection.

They then impinge on a counter rotating turbine, causing them to further loose

energy by reﬂection. The neutrons are then guided to a gravitational trap consisting

a container that is reﬂecting on the bottom and side surfaces but absorbing on the

top surface. Neutrons that are trapped must then have energies <m

gz ∼ 10

−7

where z ∼ 1 m is the vertical size of the container.

Exercises for Chapter 3 173

3.2 The explosion of the supernova SN1987A, on Feb. 23 1987, released N ∼

antineutrinos, some of which were detected by the Japanese detector of

Kamiokande. The star that had exploded, was located at a distance of R 

140, 000 light-years from Earth. The detector contained 2000 tons of water.

The particles recorded were positrons produced in the reaction

p → ne

of antineutrinos on the protons of the hydrogen atoms of H

O. The cross-

section of this reaction at the mean energy of 15 MeV of the neutrinos, is

σ =210

−45

. How many events would be expected to be recorded ?

3.3 From the level diagram in Fig. 3.5 and the data in Appendix G. calculate

the neutron energy necessary to excite the 7.459 MeV level of

Li in a collision

with

Li.

3.4 The sun has a mean density of 1.4gcm

−3

. The Thomson cross-section

of photons, produced in the solar core, on the electrons of the solar plasma is

(γ e

−

→ γ e

−

)  0.665 10

−28

. Calculate the mean free path of photons.

In their random walk across the Sun it takes the photons a time of the order

of τ  (R/l)

(l/c)  10

years to escape and reach us (the radius of the sun

is R  700.000 km). Actually, the escape time is larger  10

–10

years due

to the higher density by a factor of roughly ∼ 200 in the solar core.

3.5 Verify that if (3.37) is satisﬁed, the maximum target recoil energy is

much less than the kinetic energy of the beam particle.

3.6 Verify that the two peak energies in Fig. 3.22 correspond to elastic

scattering on protons and on

H nuclei.

3.7 By comparing the Rutherford Scattering cross-section with that of

nucleon–nucleon scattering (Table 3.3), ﬁnd the scattering angular range

where the nucleon–nucleon amplitude is larger than the Coulomb amplitude

for ∼ 2 MeV proton–proton scattering.

4. Nuclear decays and fundamental

interactions

This chapter is primarily concerned with nuclear instability. Generally speak-

ing, there are two types of decays of nuclear species: A-andZ-conserving “dis-

sociative” decays like α-decay and spontaneous ﬁssion; and β-decays which

transform neutrons to protons or vice versa. Additionally, nuclear excited

states decay by emission of photons (γ-decay) or atomic electrons (internal

conversion). If their energy is suﬃciently high, the excited states can also

decay by dissociation, especially nucleon emission.

Our ﬁrst goal in this chapter is to describe γ-andβ-decay of nuclei. The

interesting point is that in both cases these decays are due to fundamen-

tal interactions. The interactions are suﬃciently weak that the decays can

be treated with standard time-dependent perturbation theory, Appendix C.

This is quite diﬀerent from dissociative decays which are generally viewed as

tunneling processes. α-decay is treated in this way in Chap. 2 and sponta-

neous ﬁssion in Chap. 6.

The information gleaned from weak nuclear decays was instrumental in

the formulation of the Standard Model of fundamental constituents of matter,

the families of quarks and leptons, and their interactions. We will end this

chapter with a brief introduction to this model.

4.1 Decay rates, generalities

4.1.1 Natural width, branching ratios

Decay rates and mean lifetimes can be deﬁned by the same considerations

as lead us to the deﬁnition of cross-sections in Chap. 3. An unstable particle

has a probability dP to decay in a time interval dt that is proportional to dt:

dP =

, (4.1)

where τ clearly has dimensions of time and is called the “mean lifetime” of

the particle. This law governs the time dependence of the number N(t)ofan

unstable state surviving after a time t:

N(t +dt) − N(t)=−N (t)dP ⇒

= −

N(t)

, (4.2)

176 4. Nuclear decays and fundamental interactions

which has the solution

N(t)=N (t = 0)e

−t/τ

. (4.3)

The mean survival time is τ, justifying its name.

The inverse of the mean lifetime is the “decay rate”

λ =

. (4.4)

We saw in Sect. 3.5 that an unstable particle (or more precisely an un-

stable quantum state) has a rest energy uncertainty or “width” of

Γ =¯hλ =

¯h

6.58 × 10

−22

MeV sec

. (4.5)

Since nuclear states are typically separated by energies in the MeV range,

the width is small compared to state separations if the lifetime is greater

than ∼ 10

−22

sec. This is generally the case for states decaying through the

weak or electromagnetic interactions. For decays involving the dissociation

of a nucleus, the width can be quite large. Examples are the excited states

Li (Fig. 3.5) that decay via neutron emission or dissociation into

He.

From the cross-section shown in Fig. 3.4, we see that the fourth excited state

(7.459 MeV) has a decay width of Γ ∼ 100 keV.

It is often the case that an unstable state has more than one “decay

channel,” each channel k having its own “branching ratio” B

. For example

the fourth excited state of

Li has

=0.72 B

=0.28 B

∼ 0.0 , (4.6)

where the third mode is the unlikely radiative decay to the ground state. In

general we have



=1, (4.7)

the sum of the “partial decay rates,” λ

= B



= λ, (4.8)

and the sum of the “partial widths,” Γ

= B



= Γ. (4.9)

4.1.2 Measurement of decay rates

Lifetimes of observed nuclear transitions range from ∼ 10

−22

sec

Li (7.459 MeV) → n

Li,

He τ =6×10

−21

sec (4.10)

to 10

4.1 Decay rates, generalities 177

Ge →

Se 2e

−

1/2

=1.6 × 10

yr (4.11)

It is not surprising that the techniques for lifetime measurements vary con-

siderably from one end of the scale to the other. Here, we summarize some

basic techniques, illustrated in Figs. 4.1- 4.4.

• τ>10

yr (mostly α-and2β-decay). The nuclei are still present on Earth

(whose nuclei were formed about 5 × 10

year ago) and can be chemically

and isotopically isolated in macroscopic quantities and their decays de-

tected. The lifetime can then by determined from (4.3) and knowledge of

the quantity N in the sample. An illustration of this technique is shown in

Fig. 4.1.

• 10 min <τ<10

yr (mostly α-andβ-decay). The nuclei are no longer

present on Earth in signiﬁcant quantities and must be produced in nuclear

reactions, either artiﬁcially or naturally (cosmic rays and natural radioac-

tivity sequences). The lifetimes are long enough for chemical and (with

more diﬃculty) isotopic puriﬁcation. The decays can then be observed and

(4.3) applied to derive τ. The case of

170

Tm is illustrated in Fig. 4.2. If

the observation time is comparable to τ , knowledge of N(t =0)isnot

necessary because τ can be derived from the time variation of the counting

rate.

• 10

−10

s <τ <10

s(mostlyβ-, γ-andα-decay). While chemical and isotopic

puriﬁcation is not possible for such short lifetimes, particles produced in

nuclear reactions can be slowed down and stopped in a small amount of

material (Sect. 5.3). Decays can be counted and (4.3) applied to derive τ.

Examples are shown in Figs. 2.18 and 2.19. The case of the ﬁrst excited

state of

170

Yb produced in the β-decay of

170

Tm is illustrated in Fig. 4.2.

• 10

−15

s <τ <10

−10

s. (mostly γ-decay). The time interval between produc-

tion and decay is too short to be measured by standard timing techniques

but a variety of ingenious techniques have been devised that apply to this

range that covers most of the radiative nuclear decays. One technique uses

the fact that the time for a particle to slow down in a material after having

been produced in a nuclear reaction can be reliably calculated (Sect. 5.3).

For particles with 10

−15

s <τ <10

−10

s, the disposition of material can be

chosen so that some particles decay “in ﬂight” and some after coming to

rest. For the former, the energies of the decay particles are Doppler shifted

and can be distinguished from those due to decays at rest. Measurement of

the proportion of the two types and knowledge of the slowing-down time

allows one to derive τ. The technique is illustrated in Fig. 4.3.

Another indirect technique for radiative transitions is the Coulomb ex-

citation method. The cross-section for the production of an excited state

in collisions with a charged particle is measured. As mentioned in Sect.

3.4.2, the cross-section involves the same matrix element between ground-

and excited-nuclear states as that involved in the decay of the excited- to

ground-state. In fact, the incident charged particle can be considered to be

178 4. Nuclear decays and fundamental interactions

a source of virtual photons that can induce the transition. Knowledge of

the cross-section allows one to deduce the radiative lifetime of the state.

• τ<10

−12

s i.e. Γ>6 × 10

−10

MeV. (mostly γ-decay and dissociation). In

this range where direct timing is impossible, the width of the state can be

measured and (4.5) applied to derive τ. An example is shown in Fig. 3.4

where the energy dependence of the neutron cross-section on

Li can be

used to derive the widths of excited states. In this example, the state is

very wide because it decays by breakup to n

Li or

He. Widths of states

that decay radiatively can only be measured with special techniques. An

example is the use of the M¨ossbauer eﬀect, as illustrated in Fig. 4.4.

4.1.3 Calculation of decay rates

Consider a decay

a → b

+ b

+ ...+ b

. (4.12)

Particle a, assumed to be at rest, has a mass M andanenergyE = Mc

.As

in scattering theory, we can calculate decay rates by using time-dependent

perturbation theory (Appendix C). We suppose that the Hamiltonian consists

of two parts. The ﬁrst, H

, represents the energies of the initial and ﬁnal state

particles, while the second, H

, has matrix elements connecting initial and

ﬁnal states. The decay rate, i.e. the probability per unit time that a decays

into a state |f of ﬁnal particles is

a→f

2π

¯h

|f|T |a|



−





(4.13)

where E

is the energy of particle b

. In ﬁrst order perturbation theory, the

transition operator T is just the Hamiltonian responsible for the decay, H

As in the case of nuclear reactions, quantum ﬁeld theory is the appropri-

ate language to determine which decays are possible and the form of their

matrix elements. Lacking this technology, we will usually just give the ma-

trix elements for each process under consideration. However, as in reaction

theory where the classical limit of particles moving in a potential was a guide

for determining the matrix elements for elastic scattering, certain decay pro-

cesses have classical analogs that can guide us. This is the case for radiative

decays which have the classical limit of a charge distribution generating an

oscillating electromagnetic ﬁeld.

Despite the fact that we will not generally be able to derive rigorously

the matrix elements, we can expect that the interaction Hamiltonian is

translation invariant. Therefore, the square of the transition matrix element

|f|T |i|

will be, as in scattering theory, proportional to a momentum con-

serving delta function. We therefore deﬁne the “reduced” transition matrix

element

T by

|f|T |i|

= |

T (p

...p

−(N+1)

V (2π¯h)

(Σp

) , (4.14)

4.1 Decay rates, generalities 179

−

helium gas

Mo foil

100

ill

ators

ill

ato

160

120

events/0.1 MeV

0123

2 electron energy sum (MeV)

1433 events

(background subtracted)

Fig. 4.1. The measurement of the double-β decay of

100

Mo →

100

Ru 2e

−

[36].

The upper ﬁgure shows a simpliﬁed version of the experiment The source is a 40µm

thick foil consisting of 172 g of isotopically enriched

100

Mo (98.4% compared to

the natural abundance of 9.6%). After a decay, the daughter nucleus stays in the

foil but the decay electrons leave the foil (Exercise 4.2) and traverse a volume con-

taining helium gas. The gas is instrumented with high voltage wires that sense the

ionization trail left by the passing electrons so as to determine the e

−

trajectories.

The electrons then stop in plastic scintillators which generate light in proportion to

the electron kinetic energy. The bottom ﬁgure show the summed kinetic energy of

electron pairs measured in this manner. A total of 1433 events were observed over

a period of 6140 h, corresponding to a half-life of

100

Mo of (0.95 ± 0.11) × 10

yr.

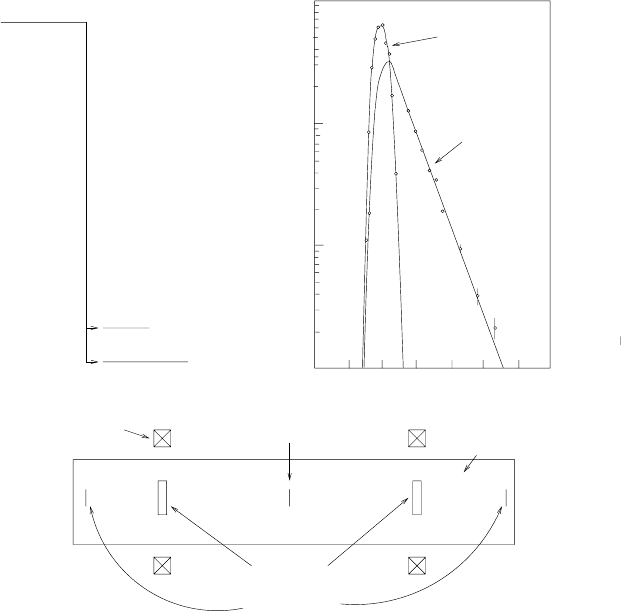
180 4. Nuclear decays and fundamental interactions

170

128.6 d1

=0.9679 MeV

24%

76%

Tm source

shielding

ill

ato

focusing

coil

vacuum

chamber

100

coincidence counting rate

−8

prompt

coincidences

84 keV

1/2

=1.57x10

−9

time delay (ns)

0.084 MeV

1.6ns

Fig. 4.2. Observation of the decay of

170

Tm and measurement of the lifetime of the

ﬁrst excited state of

170

Yb [37]. The radioactive isotope

170

Tm (t

1/2

= 128.6day) is

produced by irradiating a thin foil of stable

169

Tm with reactor neutrons.

170

Tm is

produced through radiative neutron capture,

169

Tm(n, γ)

170

Tm. After irradiation,

the foil is placed at a focus of a double-armed magnetic spectrometer. The decay

170

Tm →

170

Yb e

−

proceeds as indicated in the diagram with a 76% branching

ratio to the ground state of

170

Yb and with at 24% branching ratio to the 84 keV

ﬁrst excited state. The excited state subsequently decays either through γ-emission

or by internal conversion where the γ-ray ejects an atomic electron of the Yb.

Electrons emerging from the foil are momentum-selected by the magnetic ﬁeld and

focused onto two scintillators. Events with counts in both scintillators are due to a

β-electron in one scintillator and to an internal conversion electron in the other. The

distribution of time-delay between one count and the other is shown and indicates

that the exited state has a lifetime of ∼ 1.57 ns.