Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

160 3. Nuclear reactions

α→β

2π

¯h

|H(α)|

|H(β)|

− E

)

+ Γ

− E

) . (3.180)

We see that the probability is proportional to the square of the amplitude to

form the resonance from the initial state and to the square of the amplitude

for the decay of the resonance to the ﬁnal state. The delta function conserves

energy in the transition between the initial and ﬁnal states. The energy de-

pendence of the probability reﬂect the parameters (width and mean energy)

of the resonance.

The total cross-section is found by summing over ﬁnal states in the usual

way. The factor |H(β)|

− E

) when summed gives a factor Γ from

(3.165). Equation (3.165) can also be used to replace |H(α)|

∝ Γ/ρ(E).

The density of states is ρ ∝ VpE for a normalization volume V and center-

of-mass momentum and energy p and E. After dividing by the ﬂux density

(pc

/E)/V , one ﬁnds

σ(E)=4π



¯h



(Γ/2)

(E − E

)

+ Γ

, (3.181)

where p is the center of mass momentum. While we have found this formula

using perturbation theory, it turns out that it holds even when perturba-

tion doesn’t apply. Note that the cross-section for E = E

is the so-called

“geometrical” cross-section 4π(¯h/p)

The calculation can be generalized to include the eﬀects of spin and to

allow for the existence of several diﬀerent continuums {|α

,...,|α

} corre-

sponding to diﬀerent particles coupled to the same unstable state. Let Γ be

the total width of the resonance and the Γ

, i =1,...,n, the “partial widths”

for the channel i deﬁned by

Γ = ΣΓ

,Γ

= B

Γ, (3.182)

where B

is the branching ratio to the channel i We then have a spin averaged

cross-section

i→f

(E)=

(2J +1)

(2S

+ 1)(2S

+1)

4π



¯h



(Γ

/2)(Γ

/2)

(E − E

)

+ Γ

, (3.183)

where J is the spin of the resonance and S

and S

arethespinsofthetwo

initial state particles. The factor (2J + 1) is then due to the sum over the

possible intermediate resonant states while the factors (2S

+ 1) take into

account the fact that the widths Γ

are due to disintegration to all possible

spin states.

An example of a cross-section exhibiting resonance behavior is shown in

Fig. 3.26, showing cross-sections for neutrons on

235

Uand

238

U. The peaks

correspond to excited states of

236

Uand

239

U. The states of

239

U can only

decay by neutron or photon emission and therefore contribute to the elastic

and (n, γ) cross-sections. The states of

236

U can also decay by ﬁssion. The

dips in the elastic cross-section at energies just below some of the peaks are

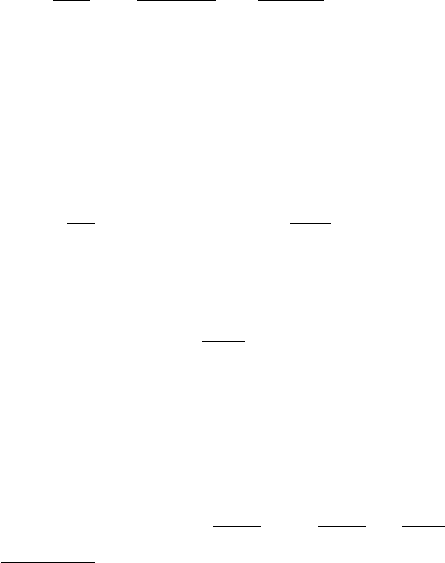
3.6 Nucleon–nucleus and nucleon–nucleon scattering 161

due to interference between the resonant amplitude and the non-resonant

amplitude.

3.6 Nucleon–nucleus and nucleon–nucleon scattering

Up to now, our analysis of scattering has been based on perturbation theory.

Here, we develop a method that is useful in calculating the elastic cross-

sections on potentials that strongly aﬀect the incoming wavefunction. It will

be most easily applied to neutron–nucleus scattering in cases where the de

Broglie wavelength, 2π¯h/p of the incident neutron of momentum p is much

larger than the range R of the potential. This is equivalent to

kR  1 (3.184)

where k = p/¯h. For neutron–nucleus scattering, this requirement is satisﬁed



(¯hc)

∼

13 MeV

2/3

(3.185)

whereweusedR =1.2A

1/3

for the nuclear radius.

3.6.1 Elastic scattering

We return to the problem ﬁrst considered in Sect. 3.3.5 of ﬁnding the eigen-

functions of the Schr¨odinger equation



¯h

∇

+ V (r)



(r)=

¯h

(r) , (3.186)

where m is the reduced mass of the neutron–nucleus system.

We will look

for solutions of the form

(r)=e

ikz

ikr

r>R (3.187)

where f is a constant independent of θ. This solution corresponds to a particle

incident in the positive z direction followed by isotropic scattering. We will

see that such a solution exists as long as (3.184) is satisﬁed. To do this, we

write (3.187) as the sum of a function that vanishes for kr  1 and a function

that depends only on r:

(r)=



ikz

−

sin kr





sin kr

ikr



r>R. (3.188)

Again, we intentionally focus on aspects which seem particularly relevant for

our discussion. The general discussion can be found in standard textbooks such

as M. L. Goldberger and K. M. Watson, Collision Theory, John Wiley & Sons,

1964.

162 3. Nuclear reactions

10 elastic

elastic (x10)

)

(n,γ)

(/100)

(n,fission) (/10

E (eV)

,γ)

(/10

−2

235

238

110

−4

−2

−4

)

cross−section (barn)

Fig. 3.26. The elastic and inelastic neutron cross-sections on

235

U (top) and

238

(bottom). The peaks correspond to excited states of

236

U and

239

U. The excited

states can contribute to the elastic cross-sections by decaying through neutron

emission. They contribute to the (n, γ) cross-section by decaying by photon emission

to the ground states of

236

U and

239

U. In the case of

236

U the states can also decay

by ﬁssion so they contribute to the neutron-induced ﬁssion cross-section on

235

3.6 Nucleon–nucleus and nucleon–nucleon scattering 163

It can readily be veriﬁed that the ﬁrst bracketed term is a solution of (3.186)

if V (r) = 0. Furthermore, the ﬁrst bracketed term vanishes in the region

r<Rwhere its two terms cancel as long as (3.184) is satisﬁed. It is therefore

a solution of (3.186) even if V =0.

The second bracketed function depends only on r:

φ(r)=

sin kr

ikr

2kr



−ikr

− (1 + 2ikf)e

ikr



. (3.189)

This function corresponds to a spherically symmetric wave directed toward

the origin (the term ∝ exp(−ikr)) and reﬂected with an amplitude propor-

tional to (1 + 2ikf). We want to ﬁnd f such that it is a solution of (3.186)

for r>R. This can be done by matching the solution for r<Rwith that

for r>Rat r = R, i.e. by requiring that the function and its derivative be

continuous at r = R.

Finding a solution of the form (3.189) is simpler task than ﬁnding a more

general solution to (3.186) because the wavefunction now depends only on

the radial coordinate r. Deﬁning

(r)=rψ

(r)

= e

−ikr

− (1 + 2ikf)e

ikr

r>R, (3.190)

(3.186) becomes



¯h

+ V (r)



(r)=

¯h

(r) , (3.191)

which is just the one-dimensional Schr¨odinger eigenvalue equation. This equa-

tion can always be solved, numerically if need be.

As a simple example, we consider the spherical square-well potential

V (r)=+∞ r<R V(r)=0 r>R, (3.192)

corresponding to an impenetrable sphere. In this case, the boundary condi-

tion is that the wavefunction vanish at the surface of the sphere, u(R)=0.

Equation (3.190) then tells us that

(1 + 2ikf)e

ikr

−ikr

⇒ f = −R (1 − ikR + ...) , (3.193)

where we have expanded in the small parameter kR  1. This gives for k → 0

dσ

dΩ

= R

⇒ σ =4πR

. (3.194)

The cross-section is 4 times the naive expectation, πR

A more realistic example that can be applied to neutron–nucleus scatter-

ing is the potential that we used to analyze the deuteron in Sect. 1.4.1:

V (r)=−V

r<R V(r)=0 r>R, (3.195)

where V

> 0. There are two interesting potentials, one for spin-aligned

nucleons (s = 1) and one for spin-anti-aligned nucleons (s = 0).

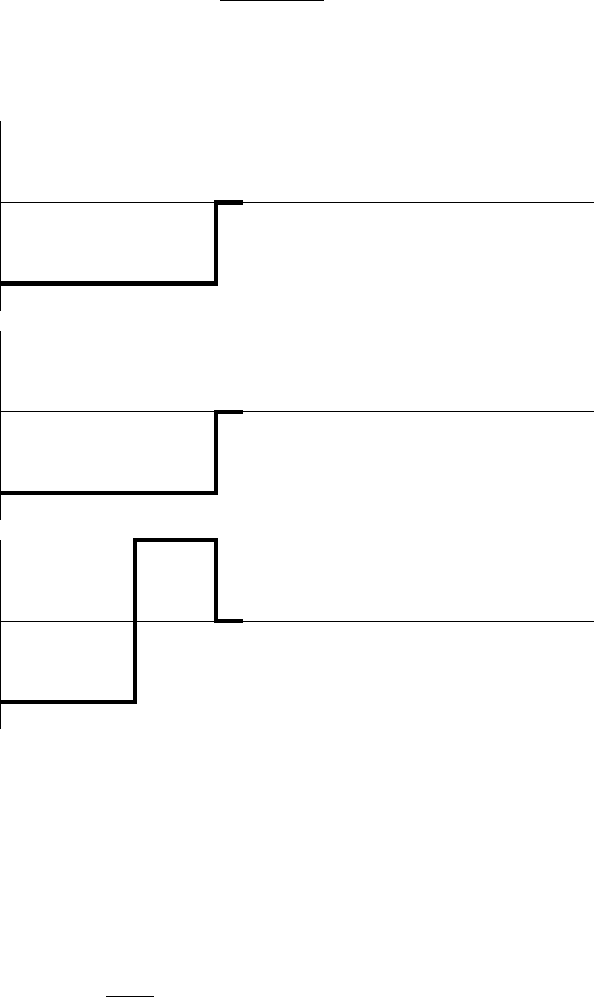
164 3. Nuclear reactions

The potential is shown in Fig. 3.27a. For r<R, the solution for p

/2m 

u(r)=A sin k





2m(V

+ E)/¯hr<R, (3.196)

where E = p

/2m =¯h

/2m.Wediscardthecosk



r solution because it

leads to a wavefunction, u(r)/r, that is singular at the origin.

exp(−ikr) − (1+2ikf)exp(ikr)

exp(−k’r) exp(−ikr) − (1+2ikf)exp(ikr)

elastic only

elastic + absorption

exp(−ikr) − (1+2ikf)exp(ikr)

exp(−k’r)

sin(k’r)

elastic + absorption with barrier

Fig. 3.27. Scattering from a spherical square-well potential. Figures a) and b)

diﬀer only in the choice of the wavefunction inside the well, the ﬁrst leading only to

elastic scattering (3.197) and the second to elastic scattering (3.208) and absorption

(3.211). The well in Fig. c) has a barrier leading to elastic scattering and absorption

proportional to the barrier penetration probability (3.216). In case (a) we require

the u(r) vanish at the origin so that the wavefunction u(r)/r is non-singular. In

cases b and c the wavefunction is assumed to be absorbed before reaching the origin.

The boundary condition is now that the r>Rsolution (3.190) and the

r<Rsolution (3.196) have the same value and derivative at r = R.This

condition is suﬃcient to determine f. In the low-energy limit, kR  1, we

have k



(E =0)=

√

2mV

/¯h and we ﬁnd

3.6 Nucleon–nucleus and nucleon–nucleon scattering 165

f(k =0) = −R



tan(

√

2mV

/¯h)

√

2mV

/¯h

− 1



. (3.197)

The pre-factor (−R) would, by itself, give a total cross-section of 4πR

.Itis

multiplied by a factor that depends on the number of neutron wavelengths,

√

2mV

/¯h that ﬁt inside the potential well. As we emphasized in Sect.

1.4.1, the two neutron–proton eﬀective potentials have approximately 1/4 of

a wavelength inside the well, i.e.

√

2mV

¯h

∼ π/2 ⇒ V

∼ 109 MeV fm

. (3.198)

For the s = 1 np system, V

is slightly greater than 109 MeV fm

the deuteron is bound. For the s = 0 system, V

is slightly less than

109 MeV fm

so there is no bound state. In the scattering problem consid-

ered here, the quarter wavelength leads to a scattering cross-section that is

much larger than 4πR

since the tangent in (3.197) is large.

Table 3.3. The low-energy nucleon–nucleon scattering amplitudes and eﬀective

ranges taken from the compilation [34]. The last two columns give the potential

parameters derived from the deuteron binding energy and the scattering formula

(3.197). Note that f  R for the s = 0 amplitudes.

fRV

(fm) (fm) (MeV) (MeV fm

)

n–p (s=1, T=0) +5.423 ± 0.005 1.73 ± 0.02 46.7 139.6

n–p (s=0, T=1) −23.715 ± 0.015 2.73 ± 0.03 12.55 93.5

p–p (s=0, T=1) −17.1 ± 0.22.794 ± 0.015 11.6 90.5

n–n (s=0, T=1) −16.6 ± 0.62.84 ± 0.03 11.1 89.5

The cross-section for the scattering on unpolarized neutrons on unpolar-

ized protons is the weighted sum of the cross-section in the (s =0)and(s =1)

state. Since there are three spin-aligned states and only one anti-aligned state

we have

n−p

=(3/4)4π|f

s=1

+(1/4)4π|f

s=0

=20.47 b . (3.199)

This corresponds to the low-energy limit of the neutron–proton cross-section

shown in Fig. 3.4. The contributions from the (s =0)and(s = 1) amplitudes

can be separated by a variety of methods. For instance, the neutron index

of refraction (Sect. 3.7) depends on the weighted sum of the amplitudes

rather than of the on the weighted sum of the squares of the amplitudes. A

166 3. Nuclear reactions

measurement of the index of refraction combined with the unpolarized cross-

section therefore allows one to deduce the amplitudes in the (s =1)and

(s = 0) states.

The measured amplitudes are listed in the ﬁrst column of Table 3.3. Also

listed are the eﬀective ranges R of the potentials. These can be found by

considering the energy dependence of the cross-section. One ﬁnds

σ(k)=

4π|f(k =0)|



1 −

f(k =0)Rk



+ |f (k =0)|

(3.200)

The cross-section slowly declines with increasing energy, as can be seen in

Fig. 3.4. The ranges deduced from the energy dependence are listed in the

second column of Table 3.3.

Quite generally, in strong interactions, one calls the quantity

a = −f(k = 0) (3.201)

the scattering length. The total low energy cross-section is therefore

σ(k  0) = 4πa

. (3.202)

We have seen in equation (3.116) that, in Born approximation, the scattering

length is related to the potential by

a =

2π¯h



V (r)d

r. (3.203)

Here, it is the more complicated relation (3.197)

It should be emphasized that (3.200) applies only to the isotropic compo-

nent of the elastic cross-section. At energies where one no longer has kR  1,

our treatment based on isotropic scattering must be modiﬁed. When the po-

tential is central (or better the interaction is rotation invariant) the complete

treatment of the angular dependence of scattering amplitudes is done by

projecting the Schr¨odinger equation on spherical harmonics. This results in

including higher “partial wave amplitudes,” each of which corresponds to

a given value of the angular momentum  so that the scattering amplitude

becomes

f(θ)=

∞



=0



(cos θ) (3.204)

where P



(cos θ) is a Legendre polynomial and where the amplitudes of the

“

” partial wave is given in terms of the “phase shifts” δ



=(2 +1)

2iδ



− 1

2ik

. (3.205)

The a



can be found by solving the partial wave Schr¨odinger equation for the

potential in question. Our original treatment based on (3.187) supposed that

f was independent of angle and therefore corresponds to keeping only the

 = 0 part of the wavefunction. The inclusion of  = 0 partial waves leads to

3.6 Nucleon–nucleus and nucleon–nucleon scattering 167

a peaking of the cross-section in the forward direction once the assumption

kR < 1 breaks down. This energy evolution of the diﬀerential cross-section

is illustrated in Fig. 3.6.

Table 3.3 also shows the amplitudes of proton–proton and neutron–

neutron scattering in the s = 0 state. (The s = 1 state is forbidden by the

Pauli principle at low energy.) The proton–proton amplitude can be derived

from large-angle scattering where Coulomb scattering is unimportant (Exer-

cise 3.7). Since neutron–neutron scattering is diﬃcult to observe directly, its

amplitude must be derived indirectly from other reactions.

We note the similarity in Table 3.3 of the amplitudes and ranges of the

three s = 0 amplitudes, n–p, p–p, and n–n. This similarity is indicative of

the isospin symmetry of the strong interactions. The three s = 0 systems

form an isospin triplet whose interactions must be identical in the limit of

isospin symmetry. There is however a large diﬀerence between the iso-triplet

potential and the iso-singlet (s = 1) potential.

3.6.2 Absorption

While our analysis was intended only for potential scattering, we can include

phenomenologically the eﬀects of absorption of the incident particle (e.g. by

radiative capture) by appropriately choosing the wavefunction for r<R.For

example, if a incoming spherical wave is completely absorbed once it enters

thenucleus,wecanuse(Fig.3.27b)

u(r)=Ae

−ik



r<R. (3.206)

This corresponds to an ingoing wave and no outgoing wave. (One can think

of the ingoing wave as being absorbed near the origin.) Requiring continuity

of the wavefunction and its derivative at r = R gives

f = −R



1 −









+ kR

−

2



, (3.207)

giving an elastic cross-section of

(k =0) = 4π



2







2mV

/¯h. (3.208)

The total (elastic + absorption) cross-section can be found from the optical

theorem to be derived in Sect. 3.7:

tot

4π Im(f)

(3.209)

which gives in this case

tot

4π



+4π



−

2



. (3.210)

Subtracting oﬀ the elastic cross-section we get the absorption cross-section:

168 3. Nuclear reactions

abs

(k → 0) =

4π



. (3.211)

The cross section is proportional to the inverse of the velocity of the incident

particle. This 1/v behavior is seen if there is a barrier-free exothermic inelastic

channel, e.g. radiative absorption (n, γ). Examples are given in Fig. 3.4.

Exothermic reactions between charged particles can only take place if

the two particles penetrate their mutual Coulomb barriers. An example is

the (p, γ) reaction in

Li whose cross-section is shown in Fig. 3.4. For such

reactions, the cross-section vanishes as k → 0 because the barrier penetration

probability vanishes for k → 0.

To see how the barrier penetration factor enters, we treat the third sit-

uation in Fig. 3.27c. There is a square potential barrier of height V

for

<r<R. The solution in this region is

u(r)=Ae

κr

+ Be

−κr

κ =



2m(V

− E)/¯h. (3.212)

Imposing the matching conditions at r = r

and r = R one ﬁnds a scattering

amplitude

f(k → 0) = −R



1 −

κR



1 − ikR



1 −

κR



2

κR



, (3.213)

where the small parameter  is proportional to the barrier penetration prob-

ability

 =



+ik



− ik

exp(−2κ(R − r

)) . (3.214)

The elastic and absorption cross-sections are

(k =0) = 4πR



1 −

κR



(3.215)

abs

4πR



1 −

κR



Im()

4πR



1 −

κR





+ k

exp(−2κ(R − r

)) . (3.216)

The absorption cross-section is proportional to the exponential barrier pen-

etration probability, as expected.

The dimensional factor in the absorption cross-section is R/k ∝ Rλ.where

λ is the de Broglie wavelength. In the more realistic case of a Coulomb bar-

rier, there is no dimensional parameter R so the cross-section must be, by

dimensional analysis, proportional to λ

. The cross-section is generally writ-

ten as

abs



2π



S(E) exp(−2πZ

α/β) , (3.217)

3.7 Coherent scattering and the refractive index 169

where S(E) is a slowly varying function of the energy and β = v/c for a rela-

tive velocity v. The exponential barrier penetration factor, derived previously

in Sec. 2.6 vanishes as the velocity approaches zero.

3.7 Coherent scattering and the refractive index

Up to now we have supposed that, in calculating the probability for an in-

teraction in a target, the scattering probability on individual target particles

can be added. This implies that the probability for an interaction after pas-

sage through a slice of matter of thickness dz is given by dP = nσdz.As

emphasized in Sect. 3.1, this is only justiﬁed if the waves emanating from the

diﬀerent target particles have random phases. Let A

= |A

iθ

be the ampli-

tude for scattering from particle i. The square of the sum of the amplitudes









i=j

||A

i(θ

−θ

)

(3.218)

For random phases, the second term vanishes and we are left with the sum

of the squared amplitudes. We will see that in the forward direction it is not

justiﬁed to assume random phases, so it is necessary to add amplitudes to

get correct results. By doing this, we will derive an expression for the index

of refraction and for the total cross-section in terms of the forward scattering

amplitude (the optical theorem).

As shown in Fig. 3.28, we consider particles incident upon a then slice

of material of thickness dz containing a density n of scatterers. Beyond the

slice, the wavefunction is the sum of the incident wave, ψ =exp(ikz)andthe

scattered wave found by summing the contributions of all scatterers:

ψ(z>0) = exp(ikz)+

ndz



dyf(θ)

exp(ik



+ y

+ z

)

+ y

+ z

)

1/2

, (3.219)

where the scattering angle is

θ(x, y) = tan

−1



+ y

. (3.220)

The exponential in (3.219) is a rapidly oscillating function of the integra-

tion variables x, y except at the “stationary point” (x =0,y =0)wherethe

phase’s partial derivatives with respect to x and y vanish. We can anticipate

that the integral will be dominated by the region near x = y = 0, corre-

sponding to θ = 0. This is just the mathematical equivalent of the physical

statement that scattering is generally only coherent in the forward direction.

We therefore replace f(θ) with f(θ = 0), set x = y = 0 in the denominator,

and expand the exponential, obtaining: