Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology
Подождите немного. Документ загружается.

4.1 Decay rates, generalities 181
target
beam
θ
detector
s
photon
germanium
1065 1085
1045
1045
1065
1085
counts per channel
θ=128
θ=24
θ=52
θ=156
E
γ
(keV)
at rest
in flight
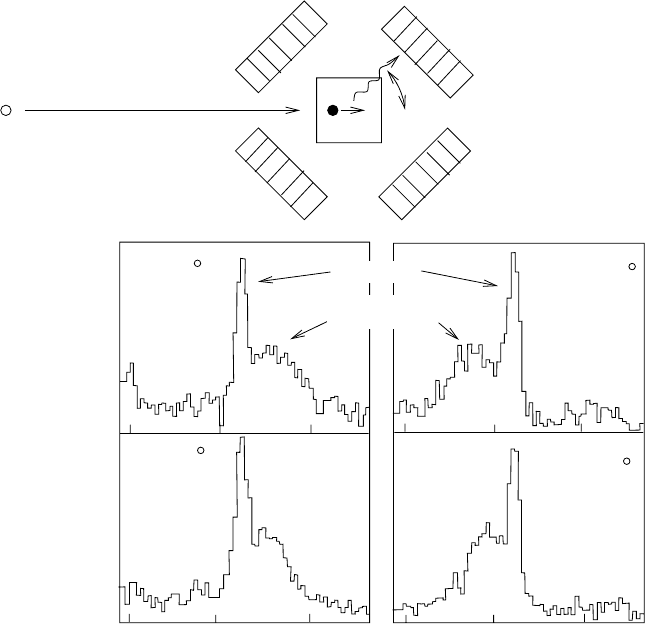
Fig. 4.3. Measurement of radiative-decay lifetimes by the “Doppler-shift attenu-
ation method” [38]. The top figure is a simplified version of the apparatus used to
measure the lifetimes of excited states of
74
Br. A beam of 70 MeV
19
F ions impinges
upon a
58
Ni target, producing a variety of nuclei in a variety of excited states. The
target is sufficiently thick that the produced nuclei stop in the target. Depending
on the lifetime of the produced excited state, the state may decay before stopping
(“in-flight” decays) or at rest. The target is surrounded by germanium-diode de-
tectors (the Euroball array) that measure the energy of the photons. The bottom
figure shows the energy distribution of photons corresponding to the 1068 keV line
of
74
Br for four germanium diodes at different angles with respect to the beam
direction. Each distribution has two components, a narrow peak corresponding to
decays at rest and a broad tail corresponding to Doppler-shifted in-flight decays.
Note that decays with θ>90 deg (θ>90 deg) have Doppler shifts that are positive
(negative). Roughly half the decays are in-flight and half at-rest. Knowledge of the
time necessary to stop a Br ion in the target allowed one to deduce a lifetime of
0.25 ps for the state that decays by emission of the 1068 keV gamma (Exercise 4.4).
182 4. Nuclear decays and fundamental interactions
E
(µ eV)
∆
0.0417
0.129
191
Os
% absorption
−4 0
4
812
v(cm/sec)
20
−20
0
40
1.0
0.8
0.6
0.4
0.2
γγ
Ir
191
v
absorber
191
Ir
γ−
detectorsource
Os
191
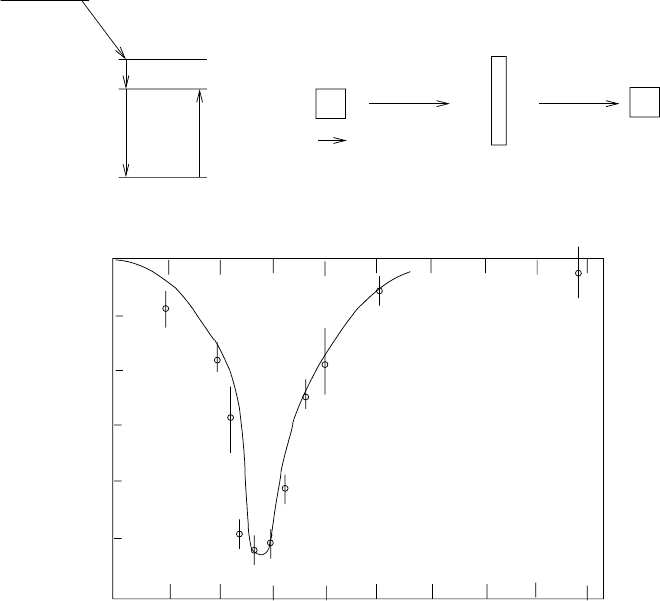
Fig. 4.4. Measurement of the width of the first excited state of
191
Ir through
M¨ossbauer spectroscopy [39]. The excited state is produced by the β-decay of
191
Os.
De-excitation photons can be absorbed by the inverse transition in a
191
Ir absorber.
This resonant absorption can be prevented by moving the absorber with respect to
the source with velocity v so that the photons are Doppler shifted out of the reso-
nance. Scanning in energy then amounts to scanning in velocity with ∆E
γ
/E
γ
= v/c.
It should be noted that photons from the decay of free
191
Ir have insufficient en-
ergy to excite
191
Ir because nuclear recoil takes some of the energy (4.42). Resonant
absorption is possible with v = 0 only if the
191
Ir nuclei is “locked” at a crystal
lattice site so the crystal as a whole recoils. The nuclear kinetic energy p
2
/2m
A
in
(4.42) is modified by replacing the mass of the nucleus with the mass of the crystal.
The photon then takes all the energy and has sufficient energy to excite the original
state. This “M¨ossbauer effect” is not present for photons with E>200 keV because
nuclear recoil is sufficient to excite phonon modes in the crystal which take some
of the energy and momentum.

4.1 Decay rates, generalities 183
˜
T represents the dynamics of the decay, as opposed to the kinematics (energy-
momentum conservation and state-counting). The factors of the wavefunction
normalization volume V = L
3
have been added for convenience so that
˜
T is
V -independent. The factor V
−(N+1)
comes from the (N + 1) wavefunctions
in the matrix element (exp(ipr)/
√
V ) while the factor V (2π¯h)
3
comes for the
square of the integration over the wavefunctions leading to the delta function
(C.24). The resulting factor of V
−N
will be canceled in the sum over final
states, as demonstrated explicitly below.
We note that the dimensionality of
˜
T depends on the number N of final
state particles:
[
˜
T ]=energy× length
3(N−1)/2
(4.15)
For N =3,asinβ-decay, it has dimensions of energy×volume and we can
anticipate that
˜
T ∼ G
F
.
The reaction rate (4.12) is obtained by summing over all possible acces-
sible final states. Just like for cross sections, one first normalizes asymptotic
final states in a finite volume V = L
3
, and one replaces the sum by integrals
over the momenta of final particles by making use of the density of states.
The normalization volume cancels off and one ends up with the general form
λ
a→b
1
+b
2
...+b
N
(4.16)
=
(2π¯h)
4
¯h
2
|
˜
T (p
1
...p
N
)|
2
δ
3
(Σp
j
)δ(E − ΣE
j
)
N
j=1
d
3
p
j
(2π¯h)
3
,
where
˜
T (p
1
...p
N
) is the reduced transition matrix element.
In the form (4.16), the transition rate appears as the square of the tran-
sition matrix element (divided by ¯h
2
) integrated over the phase space of
the accessible final states, i.e. the set of final momenta allowed by energy-
momentum conservation. The quantity
F =
(2π¯h)
4
δ
3
(Σp
j
)δ(E − ΣE
j
)
N
j=1
d
3
p
j
(2π¯h)
3
(4.17)
is called the volume of phase space. The larger this volume, the greater is the
decay rate (if all other factors are assumed to be equal).
If one is interested in angular distributions, or in energy distributions of
final particles, one restricts the integration in (4.16) to the appropriate part
of phase space.
4.1.4 Phase space and two-body decays
A simple example is that of two-body decays. Consider the decay of a,of
mass m,intoa
1
and a
2
of masses m
1
and m
2
respectively. We place ourselves
in the rest frame of a, the final momenta are opposite p
1
= −p
2
and we set
p ≡ p
1
. The energy of the final state is
184 4. Nuclear decays and fundamental interactions
E = E
1
+ E
2
=
p
2
c
2
+ m
2
1
c
4
+
p
2
c
2
+ m
2
2
c
4
(4.18)
from which follows that
p
dp
dE
=
E
1
E
2
Ec
2
. (4.19)
The decay rate is
λ =
1
4π
2
¯h
4
|
˜
T |
2
d
3
p
1
d
3
p
2
δ
3
(p
1
+ p
2
)δ(E − E
1
− E
2
) . (4.20)
The integration over p
2
fixes p
2
= −p
1
. Equation (4.19) gives p
1
dp
1
=
(E
1
E
2
/Ec
2
)d(E
1
+ E
2
) which allows a direct integration using the δ(E −
E
1
− E
2
) function. If we define the average over angles
|
˜
T |
2
=
1
4π
dΩ |
˜
T |
2
we obtain
λ =
1
¯h
pc E
1
E
2
π(¯hc)
3
E
|
˜
T |
2
(4.21)
where p is the magnitude of the momentum of each final particle.
4.1.5 Detailed balance and thermal equilibrium
In this chapter we mostly concerned with the irreversible decays of unstable
particles. However, in certain situations it is necessary to consider the inverse
of the decay. For instance, in Chap. 8 we will consider the production of
8
Be
byfusionoftwo
4
He. The
8
Be then decays back to the original
4
He pair
with a lifetime of ∼ 10
−16
s(Q = 92 keV), so we are led to consider the two
directions of the reaction
8
Be ↔
4
He
4
He . (4.22)
If Q is comparable to the temperature of the medium, the inverse decay is
possible since typical
4
He nuclei have enough kinetic energy to fuse to
8
Be.
This can be the case in stars.
In situations like this, the relative concentration of the nuclei on the two
sides of the reaction may be determined by considerations of chemical equi-
librium. For instance, if there is no
8
Be originally present, its concentration
is built up through fusion until the rate of
8
Be decay balances the rate of
8
Be
fusion. It will turn out that the relative concentrations of nuclear species will
be given by a formula (4.32) that is independent of the decay and formation
rates.
We consider a two-body decay a → bc.Thedecayrateper particle into
the momentum interval d
3
p
b
d
3
p
c
is given by (4.13) multiplied by the number
of states in d
3
p
b
d
3
p
c

4.1 Decay rates, generalities 185
λ(p
a
→ p
b
, p
c
)=
2π
¯h
|T (p
a
→ p
b
, p
c
)|
2
× δ(E
a
− E
b
− E
c
)
V d
3
p
b
(2π¯h)
3
V d
3
p
c
(2π¯h)
3
(4.23)
In the functions λ and T we have not written explicitly the spin variables, s
a
,
s
b
and s
c
. To get the decay rate within the volume V from the momentum
interval d
3
p
a
, we must multiply λ by the number of particles in this phase
space element:
Λ(p
a
→ p
b
, p
c
)=λ(p
a
→ p
b
, p
c
) n
a
Vf
a
(p
a
)d
3
p
a
, (4.24)
where n
a
is the number density and f
a
(p
a
) is the normalized spin-momentum
distribution:
s
d
3
pf
a
(p)=1. (4.25)
Once again, we do not write explicitly the spin variable s in the function f.
We want to compare this decay rate to the formation rate. Per particle
pair, this is also given by (4.13)
λ(p
b
, p
c
→ p
a
)=
2π
¯h
|T (p
b
, p
c
→ p
a
)|
2
δ(E
a
− E
b
− E
c
)
V d
3
p
a
(2π¯h)
3
. (4.26)
To get the formation rate in the volume V from the momentum interval
d
3
p
b
d
3
p
c
, we must multiply λ by the number of particles in this phase space
element:
Λ(p
b
, p
c
→ p
a
)=λ(p
b
, p
c
→ p
a
)
× n
b
Vf
b
(p
b
)d
3
p
b
n
c
Vf
c
(p
c
)d
3
p
c
, (4.27)
where n
a
and n
b
are the number densities and f
b
(p
b
)andf
c
(p
c
)arethe
normalized momentum distributions.
To find the equilibrium number densities, we need only equate the for-
mation rate (4.27) with the decay rate (4.24). Their equality at equilibrium
is due to the principle of detailed balance meaning that the rate is balanced
with the inverse rate at each point in phase space, not just globally. This is
possible if the interaction involved respects time-reversal invariance, in which
case the |T |
2
is the same for both directions of the reaction. We then get
n
b
f
b
(p
b
) n
c
f
c
(p
c
)=n
a
f
a
(p
a
)(2π¯h)
−3
, (4.28)
for all energy conserving combinations of E
a
, E
b
and E
c
. The densities and
momentum distributions are then constrained by
n
a
n
b
n
c
=(2π¯h)
3
f
b
(p
b
) f
c
(p
c
)
f
a
(p
a
)
. (4.29)
A simple situation occurs when the three species have Maxwell–Boltzmann
momentum distributions

186 4. Nuclear decays and fundamental interactions
f
i
(p
i
)=
1
2s
i
+1
1
(2πm
i
kT)
3/2
exp[−p
2
i
/(2m
i
kT)] . (4.30)
Using energy conservation
m
a
c
2
+
p
2
a
2m
a
= m
b
c
2
+
p
2
b
2m
b
+ m
c
c
2
+
p
2
c
2m
c
, (4.31)
we find that (4.29) becomes a simple relation between the densities as a
function of temperature:
n
a
n
b
n
c
=
(2s
a
+1)
(2s
a
+ 1)(2s
a
+1)
× (2π¯h)
3
m
a
2πm
b
m
c
kT
3/2
exp(−∆mc
2
/kT ) , (4.32)
where ∆m = m
a
− m
b
− m
c
. As could be expected, n
a
vanishes for kT
∆mc
2
.
Another simple situation occurs when particle c is a photon. In thermal
equilibrium, the photon phase-space density is the Planck distribution:
n
γ
f
γ
(p
γ
)=
1
(2π¯h)
3
1
exp(E
γ
/kT ) − 1
. (4.33)
Substituting this into the formation rate (4.27) it appears that thermal equi-
librium is not possible since, if we equate it with the decay rate (4.24), the
Boltzmann factors no longer cancel as they did with the Boltzmann distri-
bution. We are saved since for radiative transitions, the formation and decay
matrix elements are no longer equal because the latter is enhanced by stim-
ulated emission. This means that the decay matrix element to a given state
is multiplied by (1 + N(p
γ
), where N(p
γ
) is the number of photons already
present in the photon state:
|T (p
a
→ p
b
, p
γ
)|
2
= |T (p
b
, p
γ
→ p
a
)|
2
1+
1
exp(E
γ
/kT ) − 1
.
Substituting this into (4.24) and equating with the formation rate (4.27) we
see that the factors |T |
2
/(exp(E
γ
/kT ) − 1) nicely cancel. We then impose
energy conservation
m
a
c
2
+
p
2
a
2m
a
= m
b
c
2
+
p
2
b
2m
b
+ E
γ
, (4.34)
to find a simple expression for the ratio of the densities
n
a
n
b
=
2s
a
+1
2s
b
+1
exp(−∆mc
2
/kT ) , (4.35)
where ∆m = m
a
−m
b
. Once again, n
a
vanishes for kT ∆mc
2
. This explains
why excited nuclear states are not seen on Earth where kT ∼ 0.025 eV.
4.2 Radiative decays 187
Thermal photons can not only excite nuclei through γ(A, Z) → (A, Z)
∗
,
but also dissociate them. An example that will turn out to be very important
in cosmology is the dissociation of
2
H so we consider equilibrium
dγ ↔ pn . (4.36)
Following the same reasoning as above, the dissociation rate is
Λ(p
d
p
γ
→ p
p
, p
n
)=
2π
¯h
|T (p
d
p
γ
→ p
p
, p
n
)|
2
δ(E
d
+ E
γ
− E
p
− E
n
)
×
V d
3
p
p
(2π¯h)
3
V d
3
p
n
(2π¯h)
3
n
d
Vf
d
(p
d
)d
3
p
d
n
γ
Vf
γ
(p
γ
)d
3
p
γ
. (4.37)
We must then equate this with the rate for the inverse process. Taking into
account stimulated emission
|T (p
p
p
n
→ p
d
, p
γ
)|
2
= |T (p
d
p
γ
→ p
p
p
n
)|
2
1+
1
exp(E
γ
/kT ) − 1
,
and using the Planck relation (4.33), we find the Saha equation:
n
d
n
p
n
n
=
s
d
+1
(s
p
+ 1)(s
n
+1)
×(2π¯h)
3
m
d
2πm
p
m
n
kT
3/2
exp(−∆B/kT ) , (4.38)
where B =2.2 MeV is the deuteron binding energy. This is basically the same
equation as (4.32) except that here the two-body state has higher energy than
the one-body state.
4.2 Radiative decays
We now consider the dynamics of radiative decays. Radiative decays of atoms,
nuclei or elementary particles are those in which photons are emitted. Most
common are the decays of excited states
A
∗
→ A + γ. (4.39)
This process is also called the spontaneous emission of a photon by A
∗
.In
radiative decays of nuclei or atoms, the radiator is always much heavier than
the mass difference
m
A∗
− m
A
m
A
1 (4.40)
in which case it is simple to check that practically all the decay energy is
taken by the photon. In general we have
E
γ
=(m
A
∗
− m
A
)c
2
−
p
2
2m
A
. (4.41)

188 4. Nuclear decays and fundamental interactions
In nuclear decays, E
γ
= pc ∼ MeV and mc
2
∼ A GeV giving a nuclear recoil
of p
2
/2m ∼ 0.5keV/A, which is indeed much less than E
γ
implying
E
γ
∼ (m
A
∗
− m
A
)c
2
. (4.42)
4.2.1 Electric-dipole transitions
The quantum field theory of photons, i.e. quantum electrodynamics, is nec-
essary to derive the matrix element T for radiative transitions. Fortunately,
these transitions have the classical analog of an oscillating charge distribution
radiating a classical electromagnetic field and the formula for the radiated
power will lead us to the correct formula for the transition rate. The simplest
case is that of a single charge q moving in a 1-dimensional harmonic poten-
tial so that its position is x(t)=a cos ωt. This corresponds to an oscillating
electric dipole D
x
(t)=qa cos ωt. Classical electrodynamics can be used to
calculate the radiated power associated with the oscillating electromagnetic
field created by the oscillating dipole. The time averaged (classical) power is
given by the Larmor formula
P =
2
3
¨
D
2
t
4π
0
c
3
=
1
3
q
2
4π
0
a
2
ω
4
c
3
, (4.43)
where the
t
indicates time averaging, replacing the factor cos
2
ωt by 1/2. If
the motion is circular, the power is doubled since this corresponds to linear
harmonic motion in two dimensions.
A quantum harmonic oscillator in a state n of energy E
n
=¯hω(n +1/2)
can decay to the state n − 1 by emitting a photon of energy ¯hω.Thetime
averaged power due to this transition is
P =¯hω λ(n → n − 1) , (4.44)
where λ(n → n − 1) is the decay rate of the state n. Equating this with the
classical power (4.43) we get
λ(n → n − 1) ∼
1
¯hω
1
3
q
2
4π
0
2x
2
n
ω
4
c
3
, (4.45)
where we have equated the mean of x
2
in the state n with its classical value
a
2
/2. We have written ∼ instead of = because we expect the classical formula
to apply only in the limit n →∞. Introducing the fine-structure constant
α =e
2
/4π
0
¯hc we get a more elegant formula
λ(n → n − 1) ∼
2
3
q
2
e
2
α
x
2
n
ω
3
c
2
=
2
3
q
2
e
2
α
E
n
mc
2
ω, (4.46)
where in the second form we use x
2
n
= E
n
/(mω
2
). We see that for a
non-relativistic elementary particle (q = e), a state lives for many oscillation
periods, of order α
−1
mc
2
/E
n
.
While (4.46) turns out to be (nearly) the correct rate as calculated us-
ing quantum electrodynamics, it is not in a form that can be generalized to

4.2 Radiative decays 189
other problems. Since classically the radiation is due to the oscillating po-
sition of the particle, we would expect that the decay rate is related to the
matrix element of x taken between initial and final states, rather than the
the expectation value of x
2
in the initial state. This suggests replacing x
2
n
with
2|n − 1|x|n|
2
=
¯hn
mω
= n|x
2
|n
n
n +1/2
, (4.47)
which has the same large n limit but makes sense quantum mechanically.
Substituting this into (4.46) we get
λ(n → n − 1) =
4
3
q
2
e
2
α
ω
3
c
2
|n − 1|x|n|
2
. (4.48)
This turns out to be correct and generalizable to any transition involving a
single charged particle:
λ
i→f
=
4α
3
q
2
e
2
1
¯h
E
3
γ
(¯hc)
2
f|r|i·i|r|f . (4.49)
If we drop the assumption of a single charged particle involved in the tran-
sition, we simply replace the position vector r with D/q where D is an ap-
propriate dipole operator. Transitions governed by (4.49) are called electric-
dipole transitions or “E1” transitions for short.
Equation (4.49) is used in atomic and nuclear physics when transitions
involve, to good approximation, a single particle in which case we have q = e.
This is the case in hydrogen and alkali atoms where excited states correspond
to excitations of the valence electron that moves in the field of an inert core
that remains unaffected by the transition. In nuclear physics, the formula
applies best to even–odd nuclei where the single unpaired nucleon moves in
the potential of the paired nucleons. This is an especially good picture when
the paired nucleons form a closed shell corresponding to a magic number of
protons or neutrons.
In these cases, we need only take into account the wavefunctions, ψ(r)of
the initial and final state valence particles
f|r|i =
d
3
rψ
∗
f
(r)rψ
∗
i
(r) . (4.50)
Equation (4.49) is not very useful for precise calculations because the
nuclear matrix element of r is not easily calculable. However, it can be used
to estimate the lifetimes of atomic and nuclear excited states. We note the
presence of the fine structure constant α = e
2
/4π
0
¯hc, which represents the
square of the coupling constant of the electromagnetic field with the (charge
of the) electron. Note also the fact that the decay rate varies as the third power
of the photon energy, and as the square of the size of the system. For atomic
transitions, ¯hω ∼ eV and r∼10
−10
m which gives rates of the order of
10
7
to 10
9
s
−1
, i.e. lifetimes of the order of 10
−7
to 10
−9
s. The corresponding

190 4. Nuclear decays and fundamental interactions
width, Γ =¯h/τ ∼ 10
−7
eV is much less than the photon energy (∼ eV) but
much greater than the atomic recoil energy E
2
γ
/2m
A
c
2
∼ 10
−9
eV.
For nuclear transitions, r∼A
1/3
10
−15
mso
λ(E1) ∼ ¯h
−1
αE
3
γ
A
1/3
fm
¯hc
2
. (4.51)
For E
γ
∼ MeV, this gives rates of the order of 10
15
to 10
17
s
−1
, i.e. lifetimes
of the order of 10
−17
to 10
−15
s. The corresponding width, Γ =¯h/τ ∼ 10 eV
is much less than the photon energy.
The width is also much less than the the nuclear recoil energy E
2
γ
/2m
A
c
2
∼
10
3
eV. This has the interesting consequence that, unlike photons emitted by
atoms, photons emitted in a nuclear transition do not generally have sufficient
energy to re-excite another nucleus through the inverse transition:
E
γ
=(m
∗
− m
A
)c
2
− p
2
/2m
A
< (m
∗
− m
A
)c
2
− ¯h/τ . (4.52)
The inverse transition can only be induced in special cases where nuclear
recoil is suppressed in a crystal by the M¨ossbauer effect (Fig. 4.4) or when
the excited nucleus decays in flight with the Doppler effect compensating the
nuclear recoil (Fig. 4.19).
4.2.2 Higher multi-pole transitions
It is often the case that electric-dipole decay of an excited state is forbidden
because there are no lower-lying states for which the matrix element f|r|i
is non-zero. A famous example of this is the n =2,l = 0 state of atomic
hydrogen that cannot decay to the n = 1 state
200|r|100 =
d
3
rψ
∗
1
(r)rψ
2
(r)=0. (4.53)
The integral vanishes because the two wavefunctions are spherically sym-
metric whereas r averages to zero when integrated over all directions. This
illustrates a selection rule requiring that for E1 transitions, the parity of the
initial and final wavefunctions be different and that the angular momentum
differ by ≤ one unit.
If an E1 transition is forbidden, a state may still decay radiatively by the
action of operators that are the quantum analogs of the higher order classical
radiation processes: oscillating magnetic dipoles (M1), electric quadrupoles
(E2), etc. Each type of radiation has its own selection rules that are given in
Table 4.1. Classically, the radiated power for an oscillating l-poleispropor-
tional to ω
2l+1
so we expect the quantum transition rates to be proportional
to E
2l+1
γ
. Conventionally, one therefore writes the transition rate in the form
λ(l)=
8π(l +1)
l[(2l + 1)!!]
2
1
¯h
E
2l+1
γ
(¯hc)
2l
αB(l) , (4.54)
