Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology
Подождите немного. Документ загружается.

4.3 Weak interactions 201
e
−
neutron
0
200 400 600
800
electron kinetic energy (keV)
(N
−N
) / (N +N
)
0.06
0.04
0.02
0.00
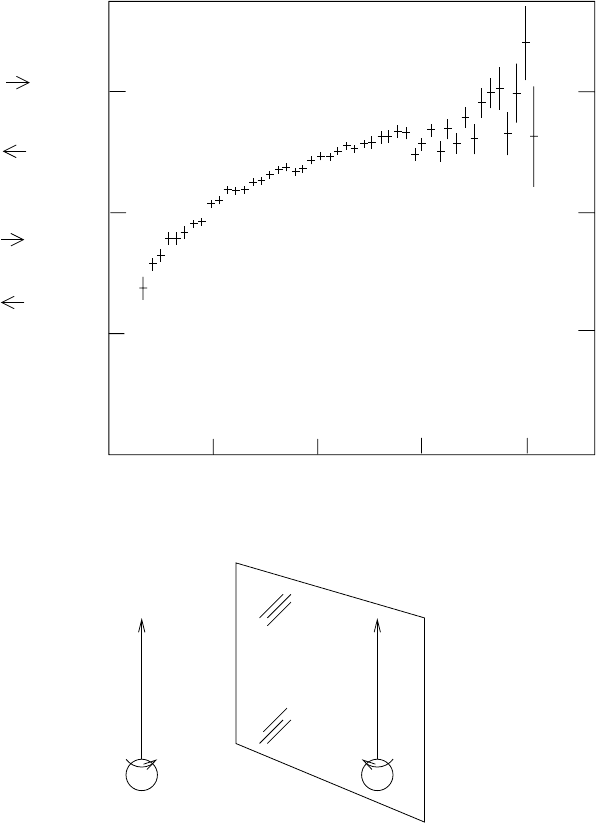
Fig. 4.10. The neutron β decay asymmetry for polarized neutrons. About 5%
more neutrons are emitted in the direction of the neutron spin than opposite the
direction of the neutron spin. This indicates that parity is violated in β-decay. This
is demonstrated in the bottom figure where a spinning neutron decays with the
electron emitted in the direction of the neutron (spin) angular momentum. Viewed
in the mirror, the spin is reversed but the direction of the electron is not. The
excess of electrons emitted in the direction of the neutron spin becomes, viewed
in the mirror, an excess of electrons emitted opposite the direction of the neutron
spin. What is viewed in the mirror does not correspond to the real world, indicating
that physics in the real world does not respect parity symmetry.

202 4. Nuclear decays and fundamental interactions
This is, again, an indication of parity violation since helicity is reversed if
viewed in a mirror. It turns out that ν
e
emitted in β
+
−decay or electron-
capture have negative helicity. The experimental demonstration of this will
be discussed in Sect. 4.3.4.
Finally, we mention the origin of the factor 2.4:
2.4G
F
∼ cos θ
c
G
F
(1 + 3g
A
)/2 . (4.81)
This formula can only be understood within the framework of the complete
relativistic theory but we see that the constant g
A
∼ 1.25 comes from the
spin-dependent couplings. Its non-integer value can be understood from the
underlying theory of quark decay. The Cabibbo angle,cosθ
c
=0.975 ±0.001,
comes from the mixing of quarks as discussed in Sect. 4.4.3.
4.3.2 β-decay of nuclei
As we already emphasized, β-radioactivity of nuclei stems from the funda-
mental processes
n → pe
−
¯
ν
e
, p → ne
+
ν
e
. (4.82)
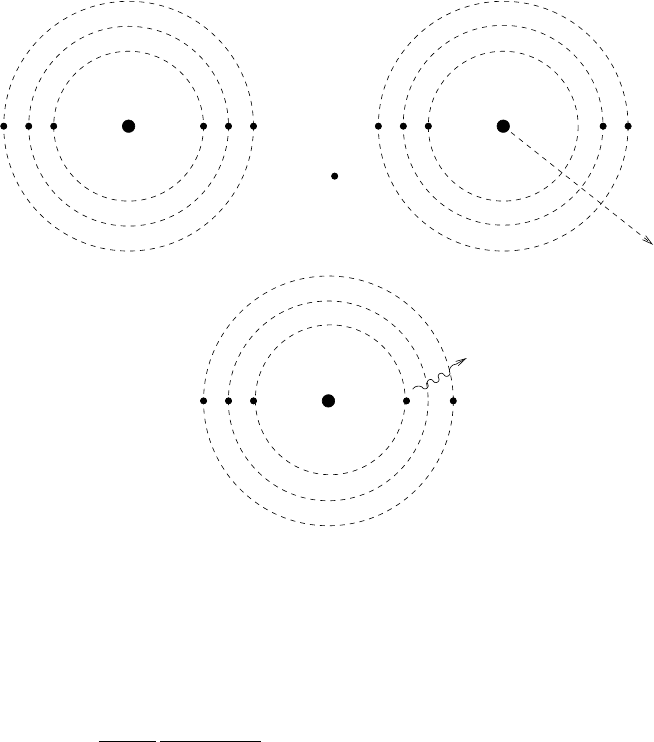
As illustrated in Fig. 4.11, it is useful to think of nuclear β-decay as neutron
or proton β-decay to empty orbitals. The decaying nucleons are considered
as moving in a fixed nuclear potential due to the other nucleons. If there
is only one Pauli-unblocked nucleon that is in a position to decay (e.g.
13
N
in Fig. 4.11), the matrix element is the same as (4.66) except that the nu-
cleon wavefunctions are not plane waves but rather normalized bound state
wavefunctions:
(A, Z + 1)e
−
¯
ν
e
|H
1
|(A, Z) =
2.4G
F
L
3
d
3
rψ
∗
p
(r)ψ
n
(r) exp[−i(p
e
+ p
ν
) · r/¯h] . (4.83)
As in neutron decay, we write 2.4G
F
to simulate a more complicated spin-
dependent matrix element that can be calculated from the underlying rela-
tivistic theory.
The matrix element (4.83) involves the Fourier transform of the product
of the initial and final nucleon wavefunctions. A useful approximation comes
about by noting that the typical lepton wavelengths, 2π¯hc/1MeV ∼ 10
3
fm
are much greater than nuclear sizes, A
1/3
fm, i.e. much greater than the extent
of the nucleon wavefunctions in (4.83). We can therefore replace the lepton
wavefunctions by their value at r = 0 and we have
(A, Z + 1)e
−
¯
ν
e
|H
1
|(A, Z) =
2.4G
F
L
3
d
3
r ψ
∗
p
(r)ψ
n
(r) . (4.84)
The matrix element is proportional to the overlap of the initial and final state
nucleons.

4.3 Weak interactions 203
e
+
ν
e
+
ν
0
+14
O 14
NN
14
0
+
1
+
γ
13
N 1/2
+
13
C 1/2
+
Fig. 4.11. Independent particle picture of nuclear β-decay. The top panel shows
the decay
13
N →
13
Ce
+
ν
e
. The decay can be considered to be the β-decay of the
valence proton that moves in the field of an inert
12
C core. The decay is shown
with no spin-flip but both flip and non-flip processes are possible. The bottom
panel shows the decay
14
O →
14
Ne
+
ν
e
. This decay is predominantly to the first
excited state (0
+
)of
14
N followed by the radiative decay to the ground state (1
+
)
(see Fig. 4.12) . For the decay of
14
O, there are two valence protons, either of which
can decay to a neutron.
The calculation of the decay rate then proceeds in the same manner as for
free neutron decay except that momentum conservation no longer holds. This
is because the initial and final nuclei are represented by a fixed potential in
which the decaying nucleon is confined. The fixed nuclear potential therefore
has effectively an infinite mass. This is just as in single-particle scattering
in a fixed potential where there was also no momentum conservation. The
differentialdecayrateis
dλ =
c
6
8π
5
¯h
2.4G
F
(¯hc)
3
2
|M|
2
δ(∆mc
2
− E
ν
− E
e
)d
3
p
ν
d
3
p
e
, (4.85)
where ∆m is the difference in nuclear masses and the matrix element M is
M =
ψ
∗
n
(r)ψ
p
(r)d
3
r . (4.86)
The differential rate (4.85) is the same as the neutron rate (4.68) except the
m
n
−m
p
is replaced with m
A,Z
−m
A,Z±1
= ∆m and a factor |M|
2
is added.
204 4. Nuclear decays and fundamental interactions
N Mg S
100%
24%
28%
47%
100%
97%
3%
0.06%
99.3%
0.6%
O
Al
Cl
14
26
34
14
26
34
70.6 s
0.72 My
6.36 s
32.0 m
1.5 s
E (MeV)
6
0
E (MeV)
6
0
0+
0+
0+
2+
2+
5+
0+
2+
2+
1+
0+
1+
3+
0+
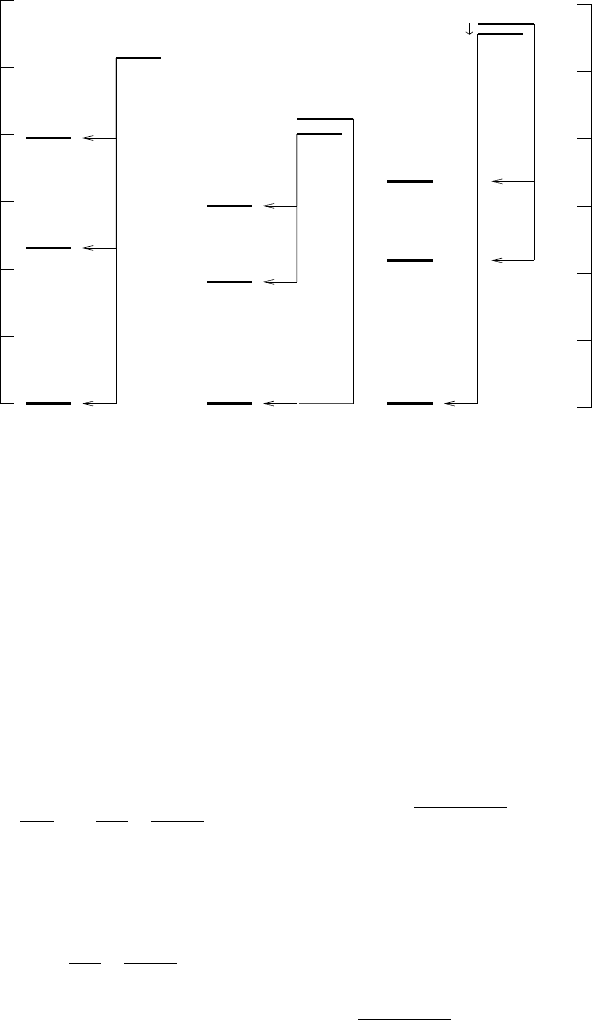
Fig. 4.12. The β-decays
14
O →
14
Ne
+
ν
e
,
26
Al →
26
Mge
+
ν
e
, and
34
Cl →
34
Se
+
ν
e
.
14
O has three allowed decays, to the ground state (Q
ec
=5.14 MeV) and to the
2.31 MeV and 3.95 MeV excited states. The highest branching fraction is for the
super-allowed decay to the 0
+
excited state.
26
Al has two β-decaying states, the
5
+
ground state and the 0+ (E =0.228 MeV) isomeric state. The later decays
via a super-allowed decay to the ground state of
26
Mg (Q
ec
=4.233 MeV). The
ground state has no allowed decays, explaining its long lifetime, t
1/2
=7.2 ×10
5
yr.
For
34
Cl, the roles of the isomer (E =0.146 MeV) and ground states are reversed
with the ground state decaying through the super-allowed mode (Q
ec
=5.49 MeV).
The isomer has two allowed β-modes to the 2
+
excited states of
34
S. The radiative
transition to the ground state of
34
Cl has a 47% branching fraction making this a
mixed β-radiative-decay.
Integrating over the neutrino momenta, we find the electron energy spec-
trum
dλ
dE
e
=
2
π
3
¯h
2.4G
F
(¯hc)
3
2
|M|
2
(∆mc
2
− E)
2
E
2
− m
2
e
c
4
E. (4.87)
The spectrum is the same as that in neutron decay with the replacement
m
n
− m
p
→ ∆m.
By integrating over the electron energy we get the total decay rate.
λ =
2
π
3
¯h
2.4G
F
(¯hc)
3
2
|M|
2
×
∆mc
2
m
e
c
2
(∆mc
2
− E)
2
E
2
− m
2
e
c
4
EdE. (4.88)
4.3 Weak interactions 205
Σ n
Ξ
Λ
−4
np 14
O
π
+
π
0
Ne
19
26m
AlAl
34
Cl
54
Fe
Σ
+
Λ
ΣΛ
Λ
p
10
1
100
Q(MeV)
10
1
10
4
8
10
λ (sec
−
1
)
5
Q
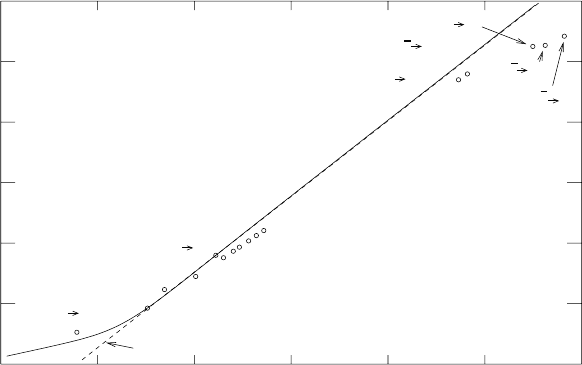
Fig. 4.13. β transition rates for super-allowed β-decays as a function of the max-
imum kinetic energy of the final electron. The decays include elementary particles
as well has nuclei where symmetry requires the integral (4.86) to be unity. The
solid line shows the phase-space integral with the dashed line corresponding to the
high-energy value Q
5
β
. The super-allowed β
+
emitters,
14
O,
26m
Al,
34
Cl,
38m
K,
42
Sc,
46
V,
50
Mn, and
54
Fe fall slightly below the line because Coulomb corrections re-
duce the rate. The strangeness-changing decays like Λ → p fall rather far below the
extrapolation because these decays are suppressed by the Cabibbo factor sin
2
θ
c
,
as discussed in Sect. 4.4.3.
TherateasafunctionofQ
β
=(∆m − m
e
)c
2
is shown in is shown in Fig.
4.13 in the case |M|
2
∼ 1. For Q
β
m
e
c
2
, the rate goes like the fifth power
of the decay energy:
λ ∼|M |
2
G
2
F
Q
5
β
. (4.89)
Generally, one has |M|
2
1, reducing considerably the rate below the
rate calculated by extrapolating from free-neutron decay. However, in certain
circumstances, isospin symmetry requires that the initial and final wavefunc-
tion overlap nearly perfectly so that |M|
2
∼ 1. Such decays are called super-
allowed decays. Three examples are shown in Fig. 4.12 and their rates are
shown in Fig. 4.13. Note that for β
+
(β
−
) decays, the Coulomb modifications
discussed below make the |M|
2
= 1 rates a bit below (above) that expected
by extrapolating from neutron decay.
In order to calculate more reliable decay rates, it is necessary to modify
(4.84) to take into account the spin of the nucleons and leptons. As in the case
of neutron decay, there are two important terms, the Fermi term proportional
206 4. Nuclear decays and fundamental interactions
to the overlap integral (4.84), and the Gamow–Teller term proportional to
the matrix element of σ between initial and final state nuclei.
Just as in radiative decays, there are selection rules governing which com-
binations of initial J
i
and final J
f
spins are possible. The Fermi term will
vanishes if the angular dependences of the initial and final wavefunctions are
orthogonal so we require
Fermi : J
i
= J
f
. (4.90)
The Gamow–Teller term can change the spin but vanishes if the initial and
final angular momenta are zero:
GT : J
i
= J
f
,J
f
± 1 J
i
= J
f
= 0 forbidden . (4.91)
Additionally, in both cases, the parity of the initial and final nuclei must be
the same. Transitions that respect the selection rules are called “Allowed”
decays. “Forbidden” decays are possible only if one takes into account the
spatial dependence of the lepton wavefunctions, i.e. using (4.83) instead of
(4.84) The examples of forbidden decays in Fig. 4.12 illustrate the much
longer lifetimes for such transitions.
β
β
_
+
p (MeV/c)
p (MeV/c)
0.2
0.2 0.6 1.0
1.4 1.8
1.8
1.4
1.00.6
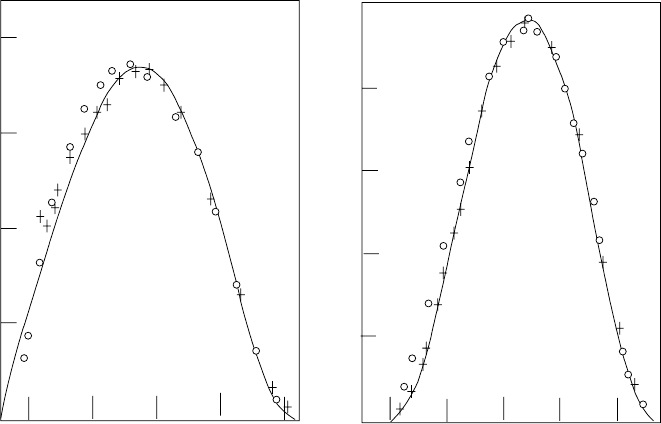
Fig. 4.14. The β
−
and β
+
spectra of
64
Cu [44]. The suppression the of the β
+
spectrum and enhancement of the β
−
at low energy due to the Coulomb effect is
seen.
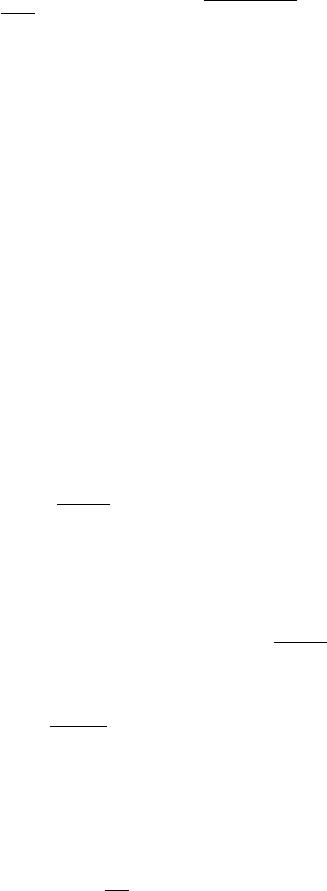
4.3 Weak interactions 207
Finally, it is necessary to take into account the fact that in the presence
of a charged nucleus, the energy eigenfunctions of the final state e
±
are not
plane waves but are suppressed (enhanced) near the nucleus for e
+
(e
−
).
This has the effect of suppressing β
+
decays at low positron energy and of
enhancing β
−
decays at low electron energy. This effect is clearly seen in Figs.
4.13 and 4.14. The spectrum (4.87) is modified as
dλ
dE
e
∝ F (Z
,E
e
) E
e
E
2
e
− m
2
e
c
4
(∆mc
2
− E
e
)
2
, (4.92)
where F (Z
,E
e
) the “Coulomb correction.” Tabulated values can be found
in [43].
4.3.3 Electron-capture
All atomic nuclei that can decay by β
+
emission can also capture an atomic
electron thereby decaying via
(A, Z)e
−
→ (A, Z − 1) ν
e
. (4.93)
This process is illustrated in Fig. 4.15. The neutrino energy is
Q
ec
=(m(A, Z) − m(A, Z − 1)]c
2
+2m
e
c
2
= Q
β+
+2m
e
c
2
. (4.94)
Electron capture is the only decay mode possible if Q
β+
< 0andQ
β−
< 0,
i.e. if the nuclear masses of neighboring isobars differ by less the the electron
mass.
The effective Hamiltonian is
(A, Z − 1)ν
e
|H
1
|(A, Z)e
−
=
2.4G
F
L
3/2
d
3
rψ
∗
p
(r)ψ
n
(r)ψ
e
(r) exp i[p
ν
· r/¯h] . (4.95)
As in the case of nuclear β-decay, we can usually make the approximation
that the neutrino and electron wavefunctions are constant over the nucleus
so that
(A, Z +1)ν
e
|H
1
|(A, Z)e
−
=
2.4G
F
L
3/2
ψ
e
(r =0)
d
3
r ψ
∗
p
(r)ψ
n
(r) .
This gives a decay rate
λ =
c
π(¯hc)
4
(2.4G
F
)
2
|ψ
e
(0)|
2
|M|
2
Q
2
ec
. (4.96)
The inner-most atomic electrons experience only the nuclear electric field so
their wavefunctions are hydrogen-like except that the potential is ∼ Ze
2
/r in-
stead of ∼ e
2
/r. The effective Bohr radius is then a factor Z smaller implying
that the wavefunction at the origin is a factor Z
3
larger:
|ψ
e
(0)|
2
∼
Z
3
a
3
0
. (4.97)
208 4. Nuclear decays and fundamental interactions
lm
mlk
(A,Z)
ν
e
(A,Z−1)
(A,Z−1)
a) b)
c)
γ
Fig. 4.15. Electron capture. After the nuclear transformation, the atom is left
with an unfilled orbital, which is subsequently filled by another electron with the
emission of photons (X-rays). As in the case of nuclear radiative decay, the X-ray
can transfer its energy to another atomic electron which is then ejected from the
atom. Such an electron is called an Auger electron.
The decay rate is then
λ =
c
π(¯hc)
4
(2.4G
F
)
2
Z
3
a
3
0
|M|
2
Q
2
ec
. (4.98)
Compared with nuclear β-decay, the Q dependence is weak, Q
2
ec
rather than
Q
5
β
. This means that for small Q
β
, electron-capture dominates over β
+
decay,
as can be seen in Fig. 2.13. The strong Z dependence coming from the de-
creasing electron orbital radius with increasing Z means that electron-capture
becomes more and more important with increasing Z.
Finally, we note that nuclear decay by electron capture leaves the atom
with an unfilled atomic orbital. This orbital is filled by other atomic electrons
falling into it and radiating photons. The photons are in the keV (X-ray)
range since the binding energy of the inner most electron of an atom of
atomic number Z is
E ∼ 0.5Z
2
α
2
m
e
c
2
=0.01 Z
2
keV . (4.99)
4.3 Weak interactions 209
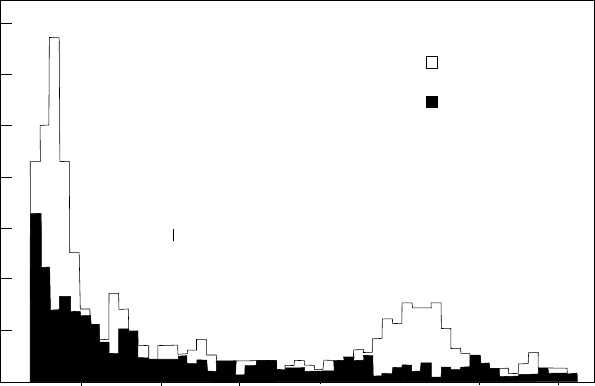
2
46
810
12 14
10
20
30−
40
50
60
70
counts
E (keV)
t > 50 days
t < 50 days
l−capture
k−capture
Fig. 4.16. The spectrum of Auger electrons from the electron-capture decay
of
71
Ge as measured by the Gallium Neutrino Observatory (continuation of the
GALLEX project). The spectrum is measured with a small gas-proportional counter
filled with a Xe − GeH
4
mixture. A small number of the germanium nuclei are ra-
dioactive
71
Ge nuclei (t
1/2
=11.4day) produced by solar neutrinos as described in
Sect. 8.4.1. Two peaks, corresponding to K- and L-capture, are observed in the first
50 days of counting. After 50 days, most of the
71
Ge has decayed and the counts
are due to ambient radioactivity due to impurities in the counter.
As in the case of nuclear radiative decays, these photons can transfer their
energy to another atomic electron that is then ejected from the atom. Such
an electron is called an “Auger electron.” Since the only high-energy particle
emitted in electron capture is a neutrino, X-rays and Auger electrons are
generally the only sure way to signal a decay be electron capture. A typical
spectrum is shown in Fig. 4.16
4.3.4 Neutrino mass and helicity
Studies of nuclear β-decay have revealed two interesting properties of neu-
trinos. The most obvious is its small mass. This is seen in the fact the the
energy spectrum of electrons is consistent with (4.87) which was calculated
assuming m
ν
= 0. A non-zero neutrino mass modifies this distribution in two
ways. First, the maximum electron energy is lowered
E
e
(max) = (m
A,Z
− m
A,Z+1
− m
ν
)c
2
. (4.100)

210 4. Nuclear decays and fundamental interactions
Second, the shape of the electron energy spectrum (4.92) is modified, espe-
cially near the “end point,” i.e. the maximum electron energy:
1
FE
e
E
2
e
− m
2
e
c
4
dλ
dE
e
∝ (E
0
− E
e
)
(E
0
− E
e
)
2
− m
2
ν
c
4
, (4.101)
where E
0
=(m(A, Z) − m(A, Z
))c
2
is the maximum electron energy in the
case m
ν
= 0. A plot of the square root of the left-hand side vs. E
e
is, for
m
ν
= 0, a straight line intersecting zero at E
e
= E
0
. Such a plot is called a
Kurie plot. As shown in Fig. 4.17, this causes the Kurie plot to curve down
near the endpoint.
pE
d λ / dE
1/2
m
ν
c
2
E
Fig. 4.17. The Kurie plot near the electron maximum energy in the case of m
ν
=0
(dashed line) and m
ν
= 0 (solid line).
Very precise measurements of the electron energy spectrum have been
made for tritium β-decay
3
H →
3
He e
−
¯
ν
e
Q
β
=18.54 keV . (4.102)
Tritium is chosen since the low value of Q
β
facilitates accurate measurements
of E
e
near the end point.
The most precise experiment to date [45] is shown in Fig. 4.18 which mea-
sures the electron spectrum with an electrostatic spectrometer. The agree-
ment of the observed spectrum with that expected for massless neutrinos,
