Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

4.4 Families of quarks and leptons 231

Consider the states |∆

 = |uuu or |∆

−

 = |ddd. These are identical

particle states whose spatial wavefunctions and spin wavefunctions are both

symmetric. This violates the Pauli Principle.

Faced with such a situation, there were three possibilities:

• forget about the quark model because it was inconsistent,

• forget about the Pauli principle,

• give new degrees of freedom to quarks so as to make the wavefunctions

antisymmetric.

The third possibility was realized in 1964 by Greenberg. His solution to

the problem consists in assuming that there exists a new quantum number

exactly conserved by all interactions, called color. At ﬁrst, this hypothesis

could appear as an artiﬁcial way to satisfy the Pauli Principle, but it turned

out to be the fundamental concept of strong interactions and it lead to the

theory of Quantum Chromodynamics.

One assumes that each quark exists in three forms of color, say blue, green

and red. (An antiquark has the complementary color of the corresponding

quark.) The color state of any three quark state is totally antisymmetric, i.e.

|ψ

qqq

 =

√

[|bgr + |grb + |rbg−|brg−|rgb−|gbr] (4.145)

Returningtothe∆

and ∆

−

, it is clear that the Pauli Principle is now

satisﬁed.

As a general fact, a fundamental property of color is that it is not ob-

servable in physical states. Nevertheless, its eﬀects are observable, as we shall

see.

The formal theory of color is performed within an exact symmetry of

fundamental interactions, based on the Lie group SU(3).

Fig. 4.27. An example of gluon exchange between two quarks (left) and between

a quark and antiquark (right).

Quarks interact by the exchange of gluons, massless particles that are

chargeless but carry one color and one anticolor, e.g. b¯r. Figure 4.27 shows

schematically how gluons are exchanged.

232 4. Nuclear decays and fundamental interactions

In quantum ﬁeld theory, it is possible to show that it is the fact that the

gluons carry a charge, i.e. color, that leads to conﬁnement, i.e. to a long-

range force that that grows linearly with separation. In electromagnetism,

the exchanged photons do not themselves carry charge and the force is not

conﬁning. It is this conﬁnement that prevents a free quark from emerging in

electron deep-inelastic scattering as shown in Fig. 3.25.

4.4.3 Quark mixing and weak interactions

It is tempting to think that the classiﬁcations of leptons and of quarks are

parallel from the point of view of weak interactions. One observes a similar

mass hierarchy with two sequences of three fermions separated by one unit

of charge. In analogy with the lepton families (4.123), we then write three

quark families as















(4.146)

In the absence of mixing, we would just have d



=d,s



=sandb



=b.The

W could induce only the transmutations u ↔ d, c ↔ sort↔ b. But then,

strange particles would be stable,sincenos→ u would exist. Unlike lepton

mixing which is manifested only in subtle eﬀects in neutrino oscillations,

quark mixing is responsible for the instability of otherwise stable particles.

If the strange and/or charm particles were stable, then we would be facing

several coexisting nuclear worlds. In addition to usual nuclei, we would see a

whole series of other nuclear species, similar but heavier. For instance, in any

nucleus, one could replace the neutron by the Λ

hyperon, which is a (u, d, s)

state of mass m

= 1116 MeV/c

. Furthermore, since the Pauli principle

does not constrain the neutron and the Λ

, the usual nuclei would possess a

larger number of heavy isotopes, since the Λ

’s can sit on the same shells as

the neutrons (in a shell model for instance).

In order to destabilize strange particles, we must have quark mixing such

that d



and b



are linear combinations of d, s and b. Generally, it is

supposed that the transformation is unitary (like the corresponding neutrino

transformation) so we write in analogy with (4.124)

⎛

⎝



⎞

⎠

⎛

⎝

⎞

⎠

⎛

⎝

⎞

⎠

where the unitary matrix can be put in the form (4.126). (The three quark

mixing angles and phase have, a priori, nothing to do with the neutrino

mixing angles.)

The elements of the mixing matrix can be determined from decay rates.

Consider the decays

n → pe

−

(i=1, 2, 3) λ =1.1 × 10

−3

−1

, (4.147)

4.4 Families of quarks and leptons 233

Fig. 4.28. Neutron decay and Λ

decay. Both can be thought of as the decay of

a quark in the presence of two spectator quarks. Both decays contain elements of

the quark and neutrino mixing matrices.

→ pe

−

(i=1, 2, 3) λ =3.2 × 10

−1

. (4.148)

Just as in nuclear physics where the β-decay of nuclei can be interpreted in

terms of the β-decay on the constituent nucleons, the decay of hadrons can be

interpreted in term of quark decay, as shown in Fig. 4.28. The quark decays

corresponding to neutron and Λ

decay are

d → ue

−

(i=1, 2, 3) , (4.149)

s → ue

−

(i=1, 2, 3) . (4.150)

The decay rates, summed over the three neutrino species, are proportional

to the squares of elements of the mixing matrix

λ(n → pe

−

ν) ∝



i=1

= |U

, (4.151)

λ(Λ

→ pe

−

ν) ∝



i=1

= |U

, (4.152)

From the ratio of the two decay rates, it is thus possible to determine the

ratio U

= tan θ

. Of course, we cannot simply equate this to the rate

ratio because of other factors in the rates. In studying neutron decay, we saw

that phase space acts as the ﬁfth power of the maximum energy of the ﬁnal

electron. Now, for Λ

decay we have p

max

= 163 MeV/c, whereas for neutron

decay p

max

=1.2MeV/c. If we deﬁne a = λ/p

max

, we obtain

a(Λ

→ p + e

−

+¯ν

)

a(n → p + e

−

+¯ν

)

∼ 0.06 ∼ tan

. (4.153)

We see that the s quark transforms much more weakly to a u than a d

quark transforms to a u quark. Conﬁrmation of this comes by comparing the

rates of K

→ µ

ν or K

−

→ µ

−

ν with π

→ µ

ν or π

−

→ µ

−

ν, Fig. 4.29.

The rates of these two weak decays should also be in the ratio tan

once

phase space is taken into account.

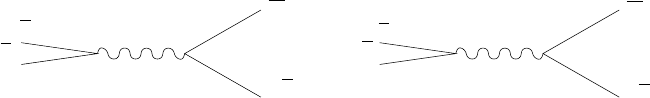
234 4. Nuclear decays and fundamental interactions

Fig. 4.29. The decays π

−

→ µ

−

and K

−

→ µ

−

. The two decays occur through

quark–antiquark annihilation by creation of a W

−

whichthendecaystoµ

−

.The

rate of pion decay is proportional to |U

while that of kaon decay is proportional

to |U

The idea of quark mixing was proposed in 1964 by N. Cabibbo. At that

time, only normal and strange hadron where known to exist. Cabibbo sug-

gested that the W couple the u quark to a linear combination of the d and s

quarks:



 =cosθ

|d +sinθ

|s (4.154)

where the value of the angle θ

, now called the Cabibbo angle, is θ

 13.1

◦

The Cabibbo theory correctly predicts the decay rates of the neutron, Λ

pions and kaons as well as the “hyperons” like Σ

(uus, m

= 1189 MeV/c

The rates of these decays are indicated on Figs. 4.13.

With the discovery of the c, b, and t quarks, we now know that the

quark mixing is a bit more complicated with the three families (4.146) mixed

according to the Kobayashi–Maskawa–Cabibbo scheme (4.4.3).

The moduli of the coeﬃcients of this matrix are now known to be in the

ranges [1]:

⎛

⎝

0.9742 to 0.9757 0.219 to 0.226 0.002 to 0.005

0.219 to 0.225 0.9734 to 0.9749 0.037 to 0.043

0.004 to 0.014 0.035 to 0.043 0.9990 to 0.9993

⎞

⎠

(4.155)

Note that, unlike the case of neutrino mixing, the diagonal elements are all

near unity so the mixing angles are all small.

It is important that the non-zero value of the phase δ implies automati-

cally the violation of CP symmetry (product of a charge conjugation and a

parity reversal). This is not of just academic interest since we will see in Chap.

9 that, in the absence of CP violation, one would expect equal amounts of

matter and antimatter in the Universe, in conﬂict with the observation that

there is very little antimatter in the observable Universe. Note that a general

2-dimensional unitary mixing matrix has no complex phase that cannot be

eliminated by a suitable redeﬁnition of the base states. Only with at least

three families is it possible to induce CP violation.

Unfortunately, it does not appear that CP violation in the quark mix-

ing matrix is directly connected with the CP violation that generated the

cosmological matter-antimatter asymmetry. Nevertheless, the 3-family-CP-

violation connection emphasizes that important eﬀects can come from the

existence of particles that do not normally appear in nature. To this extent,

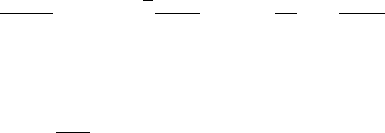
4.4 Families of quarks and leptons 235

CP violation provides a clue to the answer to Rabi’s question about the third

generation, “Who ordered that?”

The second question (and there the theory is silent at present) is why this

hierarchy of masses? In each class one has m

 m

, m

 m

. This is one of the big enigmas of present theoretical physics,

as is, in general, the question of the origin of mass of particles. This is directly

related to the third question: why these values of the Cabibbo–Kobayashi–

Maskawa angles?

4.4.4 Electro-weak uniﬁcation

Nuclear β-decay is an example of a reaction due to charged-current weak

interactions, by which we mean they are due to exchange of the charged W

We summarize the W

couplings symbolically by

−

→g(|e

 + |µ

 + |d



¯u + |s



¯c) (4.156)

Each of the terms of the right-hand-side is a decay channel of the W

−

but

they are meant to be more general than that. For instance the W

−

decays

to e

−

but it can also be emitted by a e

−

→ ν

transition. The ν

, ν



and s



are the linear combinations of the physical particles deﬁned by (4.124)

and (4.4.3). (To streamline the formulas, in this section we will ignore the

third generation of leptons and quarks.) The dimensionless coupling constant

g gives the strength of the coupling and is related to the W mass and to the

Fermi constant by





√

(¯hc)

⇒

4π

29.46

. (4.157)

Similarly for the W

if we replace fermions by their antiparticles.

In the same manner, in electromagnetic interactions, the photon is uni-

versallycoupledtotheelectricchargeand,usingthesamenotation,

|γ→

√

4πα(−|e

−

 +(2/3)|u¯u−(1/3)|d

d) (4.158)

where α is the ﬁne structure constant. We see from (4.156) that g

/4π is

the weak charged current equivalent of the electromagnetic ﬁne-structure

constant. The fact that the two ﬁne-structure constants are of the same order

of magnitude suggests they have something to do with each other, as indeed

they do.

Until 1973, one had only observed charged current weak interactions due

to the exchange of the massive W

and the electromagnetic interactions due

to the exchange of the massless photon. In 1973 it was discovered that there

were also neutral current weak interactions due to the exchange of the massive

. As we will now see, the existence of such interactions had been expected

from symmetry considerations.

236 4. Nuclear decays and fundamental interactions

Weak Isospin. From the point of view of weak interactions, quarks as well as

leptons appear as weak-isospin doublets that are mathematically equivalent

to the strong-isospin doublet formed from the u and d quarks, seen in Chap.

1. The doublets (ν

, e), (u, d



), (e

), (ν

, µ) etc.

Consider, for instance, the doublets (ν

, e) and (e

). Within this as-

sumption, we can construct a weak isospin triplet |ψ

 and a singlet |ψ

 as

follows

⎧

⎨

⎩

|ψ

 = |ν



|ψ

 =(|ν

−|e

−

)/

√

|ψ

−1

 = |e

−



(4.159)

|ψ

 =(|ν

 + |e

−

)/

√

2 . (4.160)

Note from (4.156) that the W

−

couples to |ψ

−1

 and that the W

couples

to |ψ

.ThissuggeststhatweintroduceaW

couples to |ψ

 so that the

situation is completely symmetric:

→g|ψ

 m =+1, 0, −1 . (4.161)

This relation can be extended to the other weak-isospin doublets: (ν



u) and (s



c).

Because of the triplet of W bosons, its relativistic gauge theory is said to

be based on a non-abelian group SU(2), the weak isospin.

Weak Hypercharge. One might have thought that the photon could be

identiﬁed with the W

but this is not possible, if only because it couples to

the chargeless neutrino. To ﬁnd the photon, we must ﬁrst introduce another

neutral particle, the B

that couples to the, as yet unused |ψ

 in (4.160).

We choose to make the coupling proportional to a new universal coupling

constant g



and to the weak hypercharge of the doublet in question:

Y =2(Q − T

) . (4.162)

The weak-hypercharge is equal to -1 for leptons and to 2/3 for quarks (op-

posite values for the antiparticles).

The B

couplings are then

→g



[−

√

(|ν

 + |e

−

)+(2/3)

√

(|u¯u + |d

d)+...] (4.163)

Because there is only one B

, the quantum ﬁeld theory of the B

ﬁeld is

a gauge theory on an abelian group U(1) analogous to electromagnetism.

The diﬀerence in signs of the m = 0 combinations compared to previous expres-

sions comes from the fact that we are dealing with fermion–antifermion systems

instead of fermion–fermion systems.

4.4 Families of quarks and leptons 237

The Glashow–Weinberg–Salam Mechanism. Like the W

,theB

can-

not be the photon since the coupling (4.163) is not proportional to the charge.

In particular, it couples to the neutrino. It is, however, simple to ﬁnd a linear

combination of the two neutral bosons that does have couplings proportional

to the charge: Let us therefore deﬁne :

 =cosθ

−sin θ



|γ =sinθ

 +sinθ



(4.164)

where θ

is called the weak-mixing angle or also the “Weinberg angle.”

The photon’s couplings are proportional to charge if we take

sin θ





+ g



cos θ



+ g



. (4.165)

One can check easily, restricting to the doublet (e, ν

) doublet that

|γ→−





+ g



(|ψ

−|ψ

)/

√

2=−





+ g



−

 , (4.166)

i.e. the coupling to ν

vanishes as expected for a neutral particle. This gives

us a relation with the ﬁne structure constant





+ g



= g sin θ

√

4πα , ⇒

2

4π

107.5

. (4.167)

It can be veriﬁed that the couplings of the photon to the quarks are propor-

tional to their charges.

We also need a way to ensure that the photon mass vanishes. This can be

done by considering mass-squared matrix

in the basis {|W

, |B

}

M =



−A

−Am



(4.168)

where A characterizes the W





transition which is responsible for the

mixing.

The diagonalization of this matrix is straightforward. If one wants the

photon mass to vanish, we need to take A = m

which yields by identi-

fying the eigenvectors of M with the expressions (4.164):

=0,m

= m

+ m

cos

, cos θ

.(4.169)

Why the masses squared and not the masses themselves? This is because bosons,

such as the W and B, satisfy the Klein–Gordon equation which we mentioned in

Sect. 1.4 (1.63), which involves the squares of the masses and not the masses

themselves. If one incorporates an interaction, this feature will remain. For

fermions, on the contrary, the Dirac equation is of ﬁrst order and it is directly

on the mass that one operates.

238 4. Nuclear decays and fundamental interactions

Bringing together all these results and using the values of the ﬁne-

structure constant and G

, we obtain the following masses as a function

of the weak-mixing angle θ

38.7GeV

sin θ

cos θ

(4.170)

cos

+4πα/g

=1 . (4.171)

Originally, θ

was a free parameter of the Glashow, Weinberg and Salam

model. It is now known to good precision:

sin

=0.2237 ± 0.0008 , (4.172)

=80.33 ± 0.15 GeV , (4.173)

=91.187 ± 0.007 GeV . (4.174)

We should emphasize that the question of the mass of the W and Z

is very delicate. In the relativistic formulation of the theory of Glashow,

Weinberg and Salam, a consistent quantum ﬁeld gauge theory is constructed

on a non-abelian group. This can only be done if the initial masses of the

four states |W

, |W

−

 and |B

 are all identically zero. They acquire

non-vanishing masses m

and m

by a spontaneous symmetry breaking

mechanism where Higgs bosons play a crucial role. The fact that, in the end,

the photon is a zero-mass particle is a natural automatic consequence of the

theory, and not a condition imposed on the values of parameters as we have

done above. The Higgs bosons is the last particles of the standard model that

is yet to be observed. Its couplings to the other particles are responsible for

the particle masses. An intense experimental activity is underway in order to

identify them.

We have ignored the question of helicity in our discussion of electro-weak

theory. In fact the theory is constructed so that the charged current interac-

tions maximally violate parity (as required by the observation that neutrinos

are 100% polarized) while the electromagnetic interactions conserve parity.

We see that the theory uniﬁes electromagnetic and weak interactions. It

predicts the existence of weak interactions which do not change the electric

charge. These interactions are mediated by the neutral Z

boson. An example

of such a reaction is

ν p → νp . (4.175)

It is illustrated in Fig. 4.30

The theory of neutral currents also had a role in the prediction of the

charm quark. At the time when the electroweak theory appeared, neutral

currents were unknown and only 3 quarks had been discovered, i.e. the u

The ﬁrst relation is obtained after taking into account various radiative correc-

tions. Otherwise one obtains m

=37.3GeV/ sin θ

4.4 Families of quarks and leptons 239

Fig. 4.30. Neutrino-proton elastic scattering mediated by the exchange of the Z

boson.

the d and the strange quark s. In 1970, in investigating neutral current reac-

tions, Glashow, Iliopoulos and Maiani were led to invent a mechanism which

predicted the existence of charm more than 4 years before its discovery.

As we have written the theory with the weak mixing of the quarks via

a unitary matrix (4.4.3), the Z

does not have “non-diagonal” couplings to

things like

ds. In the absence of the unitary mixing, it is readily shown that

the Z

wouldhavesuchcouplings.Inthiscase,theK

would decay to µ

−

through

ds → Z

→ µ

−

. However, the upper experimental limits on the

rate of this reaction are so low that one is sure that it is excluded up to

second order perturbation theory (to which the exchange of charged currents

and W

−

contributes in principle).

One should keep in mind the following aspects of neutral current weak

interactions of quarks.

1. The couplings of the Z

are diagonal. This boson couples to (u¯u), (d

d),

(s¯s), but not to (d¯s), etc.

2. The coupling constants have a form similar to the lepton couplings.

3. The partial decay width of the Z

into2fermionsf

f is given by

Γ (Z

→ f

f) =

48π

(|c

+ |c

) .

4. The constants |c

and |c

are such that one has

– for neutrinos : |c

+ |c

=1/2

– for e, µ, τ : |c

+ |c

=(4sin

+(2sin

− 1)

)/2 ∼ 1/4

–foru,c,t:|c

+ |c

=1/4+(1/2 − 4/3sin

)

∼ 0.29

–ford,s,b:|c

+ |c

=1/4+(1/2 − 2/3sin

)

∼ 0.37

where θ

is the Weinberg angle.

This means that the branching ratio is 6% for each neutrino species , it is

14% for d,s,b quarks (taking into account the color of quarks which multiplies

by a factor of 3 the contribution of each quark ﬂavor).

Altogether, one obtains the estimate

∼ 2.5GeV . (4.176)

240 4. Nuclear decays and fundamental interactions

E (GeV)

(nb)σ

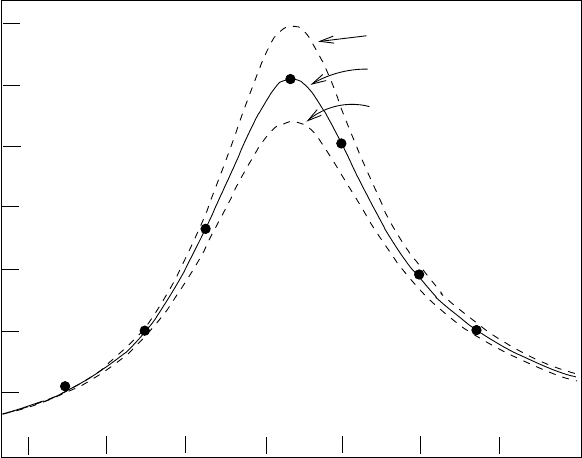
Fig. 4.31. Resonance curve of the Z

measured by the Aleph experiment at CERN

in e

−

collisions at the LEP colliding ring. The three curves represent the theo-

retical predictions according to the number of diﬀerent neutrino species. (Courtesy

Aleph Collaboration.)

We note that the existence of another, new, neutrino would increase this

width by 167 MeV, that of a new family would increase it by a factor of 4/3,

that of a neutrino and its lepton, assuming the quarks are too heavy, by 264

MeV.

We therefore understand the interest of measuring the Z

widthinorder

to count the number of diﬀerent fermions whose masses are smaller than

/2.

The answer obtained in CERN with steadily increasing accuracy since

1989 is

=2.4963 ± 0.0032 GeV i.e. N

=2.991 ± 0.016.

In other words, there are three families of quarks and leptons and only three

(neutrinos lighter that the Z

, of course).

Originally, quarks were a simple way to classify hundreds of hadrons. The

idea got enriched with the construction of quantitative dynamical models of

hadron spectroscopy.