Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

4.4 Families of quarks and leptons 221

The importance of this result is that it is a ﬁrst indication of the universal-

ity of weak interactions of leptons. The pair (e, ν

) couples to the intermediate

bosons of weak interactions in strictly the same way as the couple (µ, ν

If we compare with the calculation of the neutron lifetime, we are tempted

to think that universality extends to protons and neutrons. However, protons

and neutrons are not elementary point-like particles and we must reconsider

the problem from the point of view of quarks.

4.4 Families of quarks and leptons

The electromagnetic interactions of observed elementary particles are uni-

versal in the sense that all charges are multiples of the fundamental charge

e of the electron. At the quark level, this universality persists though the

fundamental charge is e/3.

Universality of the weak interactions is more subtle. First, the Fermi con-

stant governing weak decays, G

, is not a fundamental coupling constant

but rather an eﬀective coupling proportional to m

−2

. Second, the fact that

neutrons and protons are not fundamental particles means that fundamental

constants are renormalized by non-trivial factors when going from the quark

level to the nucleon level. This is the origin of the strange factor g

∼ 1.25 in

the eﬀective Fermi constant in β-decay (4.81). Finally, will see that even at

the quark level the fundamental couplings are not to quarks and leptons of

deﬁnite mass but rather to mixtures of quarks deﬁned by a unitary matrix.

This eﬀect is the origin of the Cabibbo angle in the eﬀective Fermi constant

(4.81).

In this section, we will go into some of the details of these problems.

4.4.1 Neutrino mixing and weak interactions

For many years, it was believed that there where three conserved “Lepton

numbers,” i.e. electron-number, muon-number, and tauon-number. The ap-

parent conservation of these three numbers meant that it was useful to classify

leptons in three generations:



−



−



−



. (4.123)

These three groups (and their antiparticles) are ordered in increasing

masses of the charged lepton:

(0.511 MeV/c

)  m

(105.6MeV/c

)  m

(1777.0MeV/c

) .

It was believed that the weak interactions do not mix these families, so that

for instance, in β-decay a e

−

) must be created in coincidence with a

(ν

) so as to conserve electron number.

222 4. Nuclear decays and fundamental interactions

In this simple picture, the weak interactions of leptons are universal.The

decay rates of the µ and τ can be calculated in a analogous manner as that of

the neutron, in terms of the Fermi constant. The decay rate of the τ lepton

can be deduced from (4.122). By changing the values of masses, we obtain the

rates for τ

−

→ e

−

and for τ

−

→ µ

−

. These reactions are interpreted

as originating in the universal coupling of the intermediate bosons W

leptons in the processes W

−

→ e

−

→ µ

−

→ τ

−

and all

corresponding crossed processes.

While this picture is consistent with most experimental results, it is now

generally believed that the ν

, ν

and ν

are in fact mixtures of three leptons

, ν

and ν

of masses m

, m

and m

⎛

⎝

⎞

⎠

⎛

⎝

µ1

µ2

µ3

τ1

τ2

τ3

⎞

⎠

⎛

⎝

⎞

⎠

. (4.124)

This fancy notation means only that the amplitude to produce a ν

paired

with a e

is proportional to U

, the amplitude to produce a ν

paired with

a µ

is proportional to U

µ2

, etc. Generally, it is supposed that the U matrix

is unitary



l=e,µ,τ

∗

= δ

. (4.125)

A3× 3 unitary matrix can be parameterized by 3 mixing angles, θ

,i=

j =1, 2, 3 and one phase angle δ [1]:

⎛

⎝

−iδ

−s

− c

iδ

− s

iδ

− c

iδ

−c

− s

iδ

⎞

⎠

(4.126)

where c

=cosθ

and s

=sinθ

To simplify things, we will ﬁrst consider the mixing of only two neutrino

species, e.g.







cos θ sin θ

−sin θ cos θ





. (4.127)

The unitary mixing matrix is now a function of a single parameter, the mixing

angle θ.

In the case of muon and electron coupling to two neutrinos, the one muon

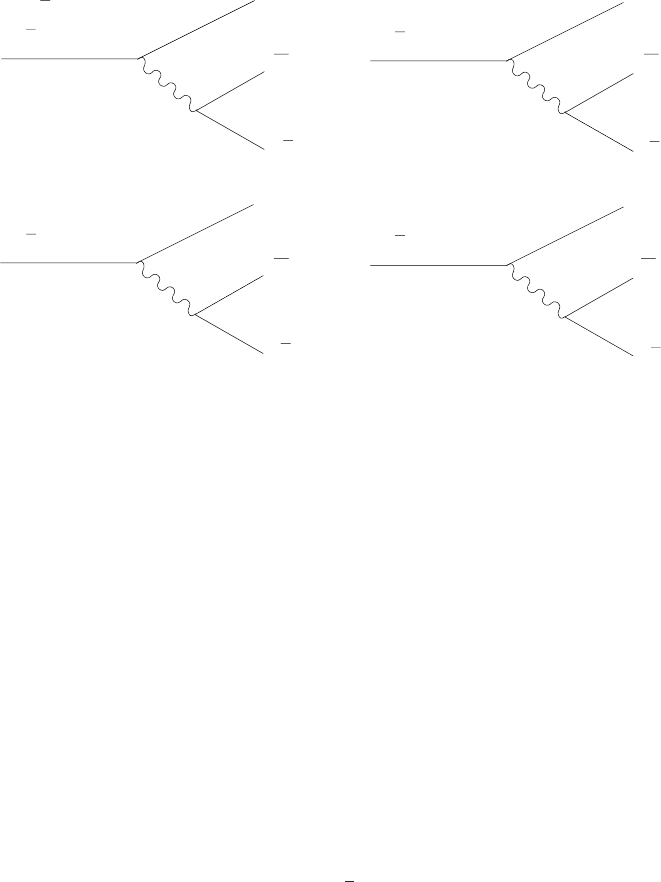
decay mode in Fig. 4.22 becomes the four modes shown in Fig. 4.23

−

→ ν

−

i=1, 2j=1, 2

The mixing angle enters into the four amplitudes as indicated in the ﬁg-

ure. For example, the amplitude for µ → eν

is proportional to cos θ sin θ.

Strangely enough, as long as all neutrino masses are much less than the

charged lepton masses so that phase-space factors for all modes are equal,

the total decay rate of the muon is unaﬀected:

4.4 Families of quarks and leptons 223

cos θ sinθ

cos θ

sinθ

cos θ

−sin

−sinθ

Fig. 4.23. The four decay modes of the muon in the case of mixing of the ν

and

. If the neutrinos all have masses that are negligible compared to the m

,the

total decay rate is unchanged from the case of no mixing shown in Fig. 4.22.

−1

∝ (cos

θ)

+(cosθ sin θ)

+(sin

θ)

=1.

The unitarity of the mixing matrix guarantees that this is the case for any

number of neutrinos.

In the case of the mixing of two neutrinos, the neutron now has two decay

modes shown in Fig. 4.24

n → pe

−

i=1, 2 .

As with the muon, the neutron lifetime is unaﬀected

−1

∝ cos

θ +sin

θ =1.

In order to see the eﬀect of the existence of multiple neutrinos, it is neces-

sary to observe the neutrinos themselves. A neutrino or antineutrino source

using nuclear β-decay produces a ν

(ν

) ﬂux proportional to cos

θ (sin

θ).

The ν

(ν

) then interact as in Fig. 4.24 with a cross-section proportional the

same factor cos

θ (sin

θ). The total neutrino interaction rate is then

Rate ∝ cos

θ +sin

θ =1−

sin

2θ. (4.128)

This is less than the rate that would be observed if there were only one

neutrino species produced in β-decay.

If this were the whole story, the existence of neutrino mixing would have

been discovered long ago. In fact, the situation is much more interesting be-

cause the neutrino masses are so small that an argument based on the uncer-

tainty principle shows that it is generally impossible to determine whether

224 4. Nuclear decays and fundamental interactions

cos θ

sinθ

Fig. 4.24. The two decay modes of the neutron in the case of mixing of the ν

and

. The total decay rate is unchanged from the case of no mixing. The

and

produced in the decay can later interact with a proton target through the reaction

νp → ne

. The total scattering rate per decay is proportional to cos

θ +sin

θ, i.e.

diﬀerent from the case of no mixing.

it was a ν

or a ν

that interacted. In this case, one should not sum the

interaction rates but rather the interaction amplitudes.

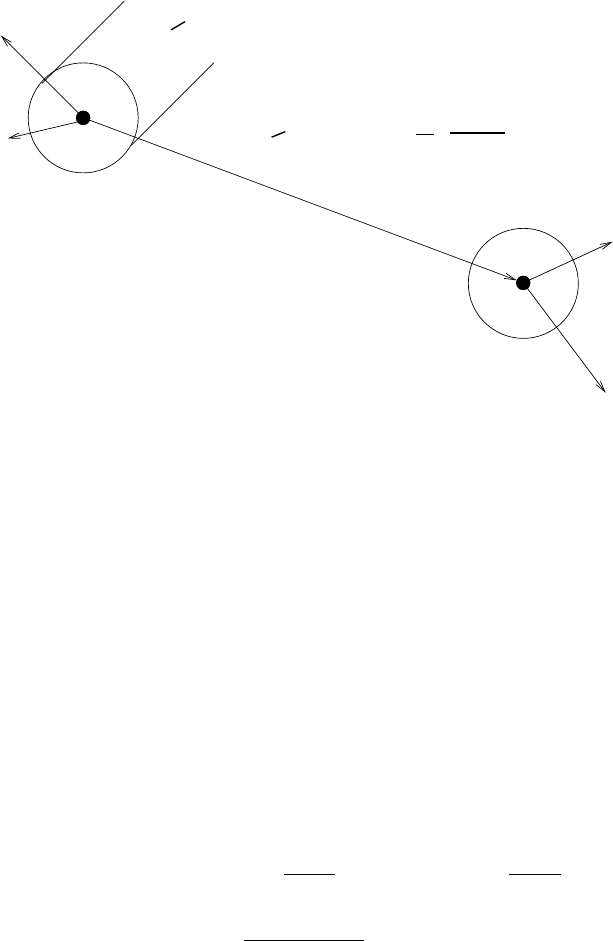
The situation is illustrated in Fig. 4.25. A nucleus (A, Z) conﬁned to a

region of size ∆x decays producing an electron of energy E

−

, a recoiling

daughter nucleus of energy E

(A,Z+1)

and a neutrino of energy E

= E

(A,Z)

−

(A,Z+1)

− E

−

. The neutrino momentum for m

 E

c ∼ E

−

. (4.129)

The two neutrino species have diﬀerent momenta but this is allowed as long

as the diﬀerence in momenta is less than the uncertainty in the momentum

of the initial nucleus

− m

<c∆p∼

¯hc

∆x

. (4.130)

If this condition is respected, both ν

and ν

emission is possible with the

identical energies for all ﬁnal-state particles. For ∆x ∼ 10

fm (corresponding

to the size of an atom) and E ∼ 1 MeV, (4.130) is respected if all neutrinos

have masses  60 keV, which is the case.

The neutrino then interacts on a proton producing a neutron of energy

and a positron of energy E

. Once again, if (4.130) is respected, ν

and

scattering can lead to ﬁnal state particles of identical energies. Since the

4.4 Families of quarks and leptons 225

h /

∆∆px

(A,Z)

exp(ipr /

pc = E

Z+1

Fig. 4.25. Neutrino production and interaction. A nucleus conﬁned to a region of

size ∆x ∼ ¯h/∆p β-decays to one of two neutrinos, ν

or ν

. If the mass diﬀerence

is suﬃciently small, (m

− m

)/2E

<∆p, then either neutrino can be produced

with the same energies for the decay products, E

Z+1

and E

e−

. The two neutrinos

can later interact and produce the same energy neutron and positron. The global

ﬁnal state, i.e. of particles produced in the decay and scatter, are identical and the

amplitudes of ν

scattering and ν

scattering must be added.

two neutrinos scatter into identical ﬁnal states, we must add the scattering

amplitudes before squaring. The amplitude for ν

∝ cos θ exp(ip

r/¯h)cosθ. (4.131)

The ﬁrst cos θ comesfromtheamplitudefortheproductionofaν

while

the second comes from the absorption. The propagation factor exp(ipr/¯h)

comes from the fact that the neutrino wavefunction enters into the absorption

amplitude. The amplitude for ν

is the same except that cos θ is replaced by

sin θ and that the neutrino momentum (4.129) is diﬀerent because of the

diﬀerent mass. The total rate is found be summing amplitudes and squaring:

λ(ν → e

) ∝



cos

θ exp



−i

¯h



+sin

θ exp



−i

¯h





=1− sin

2θ sin



− m

¯hc



. (4.132)

As a function of the distance between the decay and scatter, the rate os-

cillates about the “incoherent rate” given by (4.128). The oscillation length

corresponding to the distance between rate maxima or minima is

226 4. Nuclear decays and fundamental interactions

osc

4πE

¯hc

− m

=2.5m

1MeV

− m

1eV

. (4.133)

For r → 0 the rate reduces to the one neutrino case

λ(ν → e

) ∝ 1r L

osc

. (4.134)

In order to see the eﬀect of multiple neutrinos, it is necessary to observe them

suﬃciently far from the decay, which explains why the eﬀect is diﬃcult to

see.

On the other hand, suﬃciently far from the neutrino source, the oscilla-

tions are washed out because one must average over neutrino energies (corre-

sponding to diﬀerent oscillation phases). This averaging is necessary because

of the experimental uncertainty in the energies of the ﬁnal state particles,

and E

, in Fig. 4.25. This uncertainty generates an uncertainty in E

and therefore in the oscillation phase φ = ∆m

r/2E

¯hc. If one averages

over a neutrino energy interval ∆E

, φ is averaged over more than 2π for

r>4π¯hcE

/∆E

∆m

. This then implies that the incoherent rate is ob-

served after E

/∆E

oscillations periods:

λ(ν → e

)∝1 −

sin

2θ r 

E



∆E

osc

. (4.135)

It is also interesting to consider the production of muons by the β-decay

neutrinos:

(A, Z) → (A, Z + 1)e

−

ν followed by

ν p → n µ

. (4.136)

[This sequence would require the acceleration of the (A, Z)toanenergy

suﬃciently high to produce

ν of suﬃcient energy to produce muons, m

105 MeV.] The

→ µ

amplitude has a factor −sin θ and the

→ µ

amplitude a factor + cos θ so we get

λ(

ν → µ

) ∝



−cos θ sin θ exp



−i

¯h



+sinθ cos θ exp



−i

¯h





=sin

2θ sin



− m

¯hc



(4.137)

For r → 0, the rate vanishes because the amplitudes for the two neutrinos

cancel. This explains the “myth” of separate conservation of electron number

and muon number. Near the decay point, antineutrinos produced in decays

with electrons can only produce positrons in subsequent interactions. It was

thus natural to call these antineutrinos “

.” Further from the decay point,

the antineutrinos can also produce muons. One says that the original

have

partially “oscillated” to

Equation (4.132) can be used to determine sin

2θ and m

−m

by mea-

suring the rate as a function of the distance from the neutrino source. Exper-

iments using reactor

ν found results consistent with no mixing for r<1km

4.4 Families of quarks and leptons 227

1010

Distance to Reactor (m)

N(observed) / N(expected)

0.0

1.2

1.0

0.8

0.6

0.4

0.2

Savannah River

Bugey

Krasnoyarsk

Kamland

Chooz

Palo Verde

Goesgen

Rovno

ILL

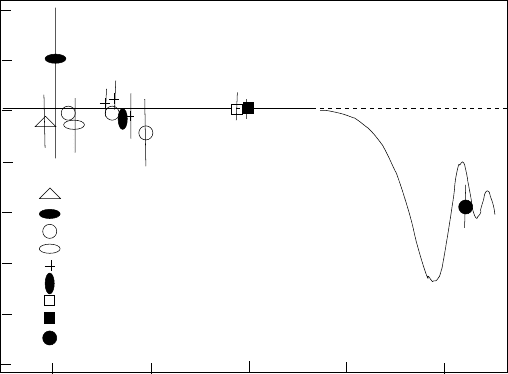
Fig. 4.26. The

detection rate vs. distance from nuclear reactors.

while the Kamland experiment [48] at r ∼ 180 km gave a rate of about

0.6 ± 0.1 times the no-mixing rate with an average antineutrino energy of

∼ 5 MeV (Fig. 4.26). Interpreting this result as a mixing between two neu-

trinos suggests

sin

2θ

> 0.510

−3

> (m

− m

> 10

−5

, (4.138)

where θ

parametrizes the mixing between ν

and ν

. Much more precise

constraints come from experiments using solar neutrinos (Chap. 8). In order

to correctly interpret these results, one needs to include the eﬀects on the

neutrino phase of the index of refraction of the solar medium. The totality

of the results imply [48]

sin

2θ

=0.84 ±0.06 (m

−m

=(7±2) ×10

−5

.(4.139)

Evidence for mixing between ν

and ν

has been found using neutrinos

from the decays of pions produced by cosmic rays in the Earth’s atmosphere

(Fig. 5.4). The dominant decay mode is π

→ µ

ν(ν) so, in the absence

of mixing, these neutrinos would be expected to produce muons through

sequences like

−

→ µ

−

ν followed by

νp → nµ

. (4.140)

The muons produced by these neutrinos scattering on protons have been

observed by the Kamiokande experiment consisting of 30 kton water instru-

mented by photomultipliers. An example of a similar detector is illustrated

228 4. Nuclear decays and fundamental interactions

in Fig. 8.14. The muons produced Cherenkov light in the water which is

detected by the photomultipliers.

The Superkamiokande experiment [49] observes that neutrinos produced

by cosmic rays in the atmosphere above the detector produce muons at the

rate expected for no mixing. On the other hand, neutrinos produced in the

atmosphere on the far side of the Earth interact at about half the expected

rate indicating maximal mixing, θ ∼ π/4. The rate deﬁcit is not compensated

by an increased production of electrons so this result is believed to indicate

mixing of ν

and ν

between ν

and ν

. The mixing angles and masses are

sin

2θ

> 0.86 (m

− m

=(3± 1) × 10

−3

, (4.141)

where θ

parametrizes the mixing between ν

and ν

The two mixing angles θ

and θ

are both nearly 45 deg indicating that

the mixing matrix (4.126) is approximately

U ∼

⎛

⎝

√

21/

√

2 s

−iδ

−1/21/21/

√

1/2 −1/21/

√

⎞

⎠

, (4.142)

where the third mixing angle is small: s

 1andc

∼ 1. It can be

measured by observing ν

→ ν

oscillations. A non-vanishing phase δ would

induce CP violation so that ν

→ ν

oscillations would not have the same

rate as

→

oscillations. Eﬀorts are underway to determine these last two

parameters of the neutrino mixing matrix.

4.4.2 Quarks

The quark model. The quark model was imagined by Gell-Mann [51] in

1964. Since then, it has received considerable experimental conﬁrmation. This

model consists in constructing the hundreds of hadrons which were discovered

in the years 1960–1980 with a simple set of point-like fermions, the quarks.

Just as for leptons, there exist two series of three quarks which can be

classiﬁed by the mass hierarchy. For leptons we have

q = −1: e

−

q =+1: e

q =0: ν

q =0:

where ν

, ν

and ν

are actually mixtures of ν

, ν

and ν

. For quarks we

have

q = −1/3: d s b q =+1/3:

d¯s

q =+2/3: u c t q = −2/3: ¯u¯c

For the moment, we ignore the possibility of quark mixing so that we pair

the d-quark with only the u-quark, etc.

Two types of hadrons have been observed

Recently, evidence has been presented for the production of a particle consisting

of three quarks and a quark–antiquark pair [50].

4.4 Families of quarks and leptons 229

• The baryons,arefermions composed of three quarks,

• The mesons are bosons composed of a quark and an antiquark.

For example, the proton and the neutron are bound states of “ordinary,”

or light quarks of the type:

|p = |uud, |n = |udd . (4.143)

The π

mesons, of spin zero and mass m

 140 MeV, are states :

|π

 = |u

d|π

 =

√



|u¯u + |d

d



|π

−

 = |d¯u . (4.144)

“Strange ” particles are obtained by substituting a strange quark s for a

u or d quark in an ordinary hadron. For instance the Λ

hyperon, of mass

= 1115 MeV/c

is a state |Λ

 = |uds, to be compared with the neutron

|n = |udd; the strange K

−

meson is a state |K

−

 = |s¯u to be compared

with |

−

 = |d¯u. Similarly, one constructs charm particles by substituting

a charm quark c to the quark u. One observes, for instance, particles which

have both charm and strangeness such as |D

 = |c¯s, and so on.

Quarks at ﬁrst appeared simply to provide a handy classiﬁcation scheme

for the observed hadrons. The experimental indication of the actual “exis-

tence” of quarks was given in 1969. In “deep inelastic scattering ” of electrons

on nucleons, we saw in Sect. 3.4.2 that the scattering cross-section is directly

related to the elementary cross-section on the constituent particles, i.e. the

quarks. As it turns out, the observed electron–quark scattering cross-section

corresponds to that of scattering on point-like spin 1/2 particles of charges

2/3and−1/3.

With our present methods of investigation, quarks present neither an

internal structure nor excited states. The charm quark was discovered in

1974. The bottom quark b was discovered shortly after in 1976. The top

quark t was only discovered in 1995, because of its high mass.

The original idea of Gell-Mann was to put some order in the hundreds of

hadrons that were continually discovered. It is remarkable that this is possible

with such a minimal set of elementary constituents.

Basic Structure of the Model.

1. Quarks have spin 1/2. This is necessary since some hadrons have half-

integer spins. One cannot construct a half-integer spin starting from in-

teger spins, but the reverse is possible.

2. Baryons are bound states of three quarks |q

 (antibaryons of three

antiquarks). Therefore, the baryon number of quarks is B =1/3 (the

baryon number of antiquarks is -1/3). Baryonic spectra correspond to

the three-body spectra of (q

) systems.

3. Mesons are quark–antiquark states |q

¯q

. The meson spectrum is the

two-body spectrum of (q

¯q

) systems.

4. Quark electric charges are fractional: +2/3 or -1/3 (antiquarks: -2/3 or

+1/3).

230 4. Nuclear decays and fundamental interactions

5. In addition to electric charge and baryon number, other additive quantum

numbers are conserved in strong interactions: strangeness s,charmc,

beauty b and top t. One therefore attributes a ﬂavor to each quark. This

is an additive quantum number which is conserved in strong interactions

(an antiquark has the opposite ﬂavor). The ﬂavor of a hadron is the sum

of ﬂavors of its constituent quarks.

6. The u and d quarks are called “usual ” quarks. They are the constituents

of the protons and neutrons and are therefore the only quarks present in

matter surrounding us. One can convince oneself that the conservation of

the u and d ﬂavors amounts simply to the conservation of electric charge.

7. Quarks are conﬁned in hadrons. The observable free (asymptotic) states

are baryons (3 quarks states) and mesons (quark–antiquark states). In

fact, the interaction that binds quarks corresponds to a potential which

increases linearly at large distances. If one attempts to extract a quark

from a hadron, it is necessary to provide an amount of energy which, at a

certain point, will be transformed into quark–antiquark pairs. These pairs

rearrange themselves with the initial quarks to materialize the energy in

the form of new hadrons. (In some sense, this phenomenon is similar to

what happens if one tries to separate the north and south poles of a

magnet.)

8. “Bare ” masses

of quarks are

 7.5MeV ∼ m

 4.2MeV  m

 150 MeV

 m

 1.5GeV  m

 4.2 GeV  m

 175 GeV.

Color . Among the excited states of the proton and neutron, a “resonance”

has been known since the 1950’s. it is called the ∆ of mass m = 1232 MeV

and spin-parity J

=3/2

. It is an isospin quadruplet T =3/2, the ∆

the ∆

,the∆

and the ∆

−

of similar masses (between 1230 and 1234 MeV).

In the quark model, the quark content of these particles is simple:

|∆

 = |uuu, |∆

 = |uud|∆

 = |udd|∆

−

 = |ddd .

But this is a catastrophe! In this construction, the Pauli principle is violated.

In fact, the states ∆ are spin excitations of the nucleons. They are the

ground states of three u or d quarks in the total spin state J

=3/2

Unless a serious pathology occurs in the dynamics, the ground state of a three

particle system has a zero total orbital angular momentum, and, likewise, all

the relative two-body orbital angular momenta are zero. Therefore, the spatial

wavefunction of the three quarks is symmetric, and in order to ensure that

the spin of the three quark system be J

=3/2

, the three spins must be

aligned, i.e. the total spin state must be symmetric.

Since quarks are permanently conﬁned in hadrons, it is not possible to observe

the mass of a free quark. We use a terminology of solid-state physics which

corresponds to the fact that the particles are permanently interacting with their

environment.