Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

4.2 Radiative decays 191

where (2l +1)!!=(2l + 1)(2l −1)(2l −3) ....Thereduced transition rate B(l)

contains all the (diﬃcult) nuclear physics and has dimension of length

.From

(4.49) we see that for E1 transitions we have

B(E1) = (f|r|i·i|r|f) ∼ R

. (4.55)

Dimensional analysis suggest that higher order elements are of order

B(El) ∼ R

. (4.56)

It turns out that this formula generally overestimates transition rates, with

the exception of electric quadrupole transitions (E2) as discussed below.

Just as higher classical multi-poles are less eﬃcient radiators than classical

electric dipoles, the quantum radiative rates decrease with increasing pole

number:

λ(El)

λ(E1)

∼



¯hc



∼



(MeV)A

1/3

200



, (4.57)

i.e. about 2 orders of magnitude per pole.

Magnetic l-pole radiation is weaker than the corresponding electric l-pole

radiation because ﬁelds generated by oscillating currents are smaller than

ﬁelds generated by oscillating charges by a factor v/c where v is the velocity

of the radiating charge. The uncertainty principle suggests that the velocity

of nucleons in nuclei is of order ¯h/(Rm

) so we expect

B(Ml) ∼



¯hc



B(El)=



1/3



B(El) . (4.58)

This implies that Ml transitions have rates between those of El and E(l +1)

transitions.

Table 4.1. Selection rules for radiative transitions

angular

type symbol momentum parity

change |∆J|≤ change

electric dipole E1 1 yes

magnetic dipole M1 1 no

electric quadrupole E2 2 no

magnetic quadrupole M2 2 yes

electric octopole E3 3 yes

magnetic octopole M3 3 no

electric 16-pole E4 4 no

magnetic 16-pole M4 4 yes

192 4. Nuclear decays and fundamental interactions

E(MeV)E(MeV)

τ (sec)

−6

−12

0.10.01 0.1 11 0.01 10

Fig. 4.5. Lifetimes of excited nuclear states as a function of E

for various electric

and magnetic multipoles.. The various multipoles separate relatively well except

for the E1 (open circles) and E2 (crosses) transitions that have similar lifetimes.

(For clarity, only 10% of the available E1 and E2 transitions appear in the plot.)

The surprising strength of the E2 transitions is because they are generally due to

collective quadrupole motions of several nucleons, whereas E1 transitions can often

be viewed as single nucleon transitions.

4.2 Radiative decays 193

Figure 4.5 shows the lifetimes of radiative transitions as a function of E

and of multipole. The expected rate decrease with increasing multipole and

decreasing E

is evident. The longest lived states appearing in the plot are

the M4 transition

108

Ag(6

109.44 keV) →

108

Ag(2

−

79.13 keV) t

1/2

= 418 yr ,

and the E5 transition

192

Ir(11

−

168.14 keV) →

192

Ir(6

12.98 keV) t

1/2

= 241 yr .

The existence of such long-lived isomeric states is only possible because the

nucleus is isolated from its environment by its atomic electrons. Long-lived

atomic states are not possible because they de-excite during frequent colli-

sions with other atoms.

There also exist a few exceptionally short-lived nuclear states. An example

is the E1 transition

B(1/2

−

320 keV) →

Be(1/2

) γ (320 keV) τ = 166 fs . (4.59)

The lifetime is much shorter than those shown in Fig. 4.5. This is explained

by the fact the

Bisahalo nucleus consisting of a single neutron orbiting

far from a

Be core [7]. This loosely bound nucleus has only two states, the

ground state and the 320 keV state. The short lifetime is due to the large

radius of the nucleus [see eq. (4.56)] and to the large matrix element for the

simple one-particle wavefunctions.

Except for the case of E2 transitions, (4.56) tends to overestimate the

rates. E2 transition rates are underestimated because these transitions are

often due to the collective motions of deformed nuclei with permanent

quadrupole moments, so the eﬀective charge involved in the transition is

large, q>e. In this case, the reduced matrix element for an E2 transition for

a state of angular momentum j to a state j − 2is

αB(E2) =

8π

j(j − 1)

(2j − 1)(2j +1)

, (4.60)

where Q

is the permanent electric quadrupole moment. This relation com-

bined with lifetime measurements can be used to estimate nuclear deforma-

tions (Fig. 1.8).

4.2.3 Internal conversion

Whereas an isolated excited nucleus decays by photon emission, an excited

nucleus surrounded by atomic electrons can also decay by transferring energy

to an atomic electron which is ejected from the atom. This process, called

internal conversion, can be thought of as the two-step process illustrated in

Fig. 4.6 where the photon emitted by the excited nucleus is absorbed by

an atomic electron which is subsequently ejected. The energy of the ejected

electron is the photon energy minus the binding energy of the electron. One

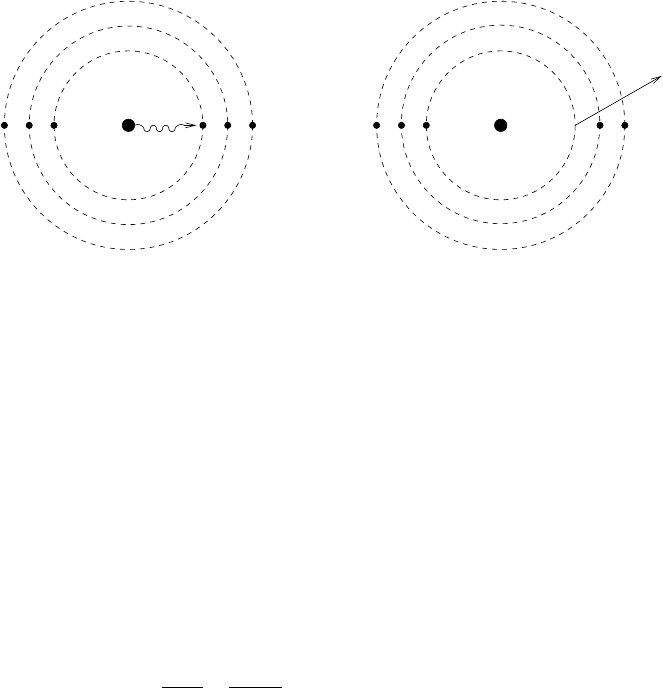
194 4. Nuclear decays and fundamental interactions

−

mlk

Fig. 4.6. An excited nucleus can transfer its energy to an atomic electron which is

subsequently ejected from the atom. The process is called “internal conversion.” The

ejected electron can come from any of the atomic orbitals. In the ﬁgure, an electron

from the deepest orbital is ejected, so-called K-conversion. Ejection of electrons in

higher orbitals (L-, M- ... conversion) are generally less probable.

denotes K-, L-, or M-conversionasejectionofanelectronfromorbital1,2,

or 3 (beginning with the inner most). Generally speaking K conversion is the

most likely.

While it is intuitive to think of internal conversion as a two-step process,

it must be remembered that it is, in fact, a single quantum process whose

amplitude can be calculated by standard perturbation theory.

The amplitude for internal conversion is proportional to the same nuclear

matrix element responsible for radiative decay. The factor of proportionality

depends on the multipolarity of the transition. An approximate expression

for the probability for K-conversion compared to that for γ-emission is

∼ Z

l +1





l+5/2

. (4.61)

This formula applies in the limit α

 1 and only if the atomic-electron

binding energy is negligible compared to E

.Itimpliesthatinternalconver-

sion dominates over γ-emission for low-energy transitions:

< (Z

)

1/(l+5/2)

. (4.62)

SincewealwayshaveZ

< 1 this means that internal conversions is negli-

gible for E

. For E1 transitions, internal conversion is almost always

small but for large l it becomes increasingly dominant for E

.In

all circumstances, numerical values α

can be derived. These estimates are

suﬃciently accurate that the multipolarity of a transition can usually be de-

termined if the conversion factor is measured. This is an important element

in the assignment of spins and parities to nuclear states .

4.3 Weak interactions 195

137

7/2

11/2

3/2

γ (90%)

internal conversion

(10%)

beta spectrum

137

ect

n m

137

Ba internal

conversion

Fig. 4.7. The β-spectrum of

137

Cs and the internal conversion lines from the decay

of the ﬁrst excited state of

137

Ba [40]. Captures from the K, L and M orbitals are

seen.

4.3 Weak interactions

Whereas the electromagnetic interactions responsible for the radiative decays

conserve the number of protons and the number of neutrons, the weak inter-

actions transform protons to neutrons or vice versa as well as the numbers

of charged leptons and numbers of neutrinos. The archetype of a weak decay

is nuclear β-decay

(A, Z) → (A, Z ±1) e

−

) ν

(

) . (4.63)

Fermi gave a remarkably eﬃcient theory of this process as soon as 1933. The

structure of this theory became more profound in 1968 with the advent of

196 4. Nuclear decays and fundamental interactions

the uniﬁed theory of weak and electromagnetic interactions due to Glashow,

Salam and Weinberg.

4.3.1 Neutron decay

In the Fermi theory, neutron decay n → pe

−

is a point-like process. This

is similar to what we discussed in Chap. 3, concerning the small range of

weak interactions owing to the large masses of intermediate bosons. Here,

the neutron transforms into a proton and a virtual W

−

boson, which itself

decays into e

−

. This process is shown schematically in Fig. 4.8.

Fig. 4.8. Neutron decay.

To ﬁnd the matrix element for neutron decay we ﬁrst recall the matrix

element for scattering of two free particles, as discussed in Sect. 3.4.1. If the

two particles 1 and 2 interact via a potential V (r

−r

), then the scattering

element is

f|V |i =



i(p

−p



)·r

/¯h

i(p

−p



)·r

/¯h

V (r

− r

where p

and p



are the initial and ﬁnal momenta for particle 1, and likewise

for particle 2. The weak interactions can be described by a delta-function

potential V ∼ Gδ(r

− r

) so the matrix element is

f|V |i =



i(p

−p



)·r /¯h

i(p

−p



)·r /¯h

r . (4.64)

There is a factor exp(ip·r) for each initial-state particle and a factor exp(−ip·

r) for each ﬁnal-state particle. This suggests that for neutron decay we use

the matrix element

pe

−

|n =

2.4G



r exp[i(p

− p

) · r/¯h] . (4.65)

The factor 2.4G

is the eﬀective G for neutron decay and will be discussed

below. Since we will not always want to use plane waves, we also write the

more general matrix element as

4.3 Weak interactions 197

pe

−

|n =2.4G



rψ

∗

(r)ψ

(r) . (4.66)

The integral in (4.65) will give a momentum conserving delta function so

we ﬁnd that the transition amplitude deﬁned by (4.14) is constant

T |

=(2.4G

)

. (4.67)

The fact that

T is constant means that the Hamiltonian has no preference

for particular ﬁnal states as long as they conserve energy and momentum.

Using (4.16), the diﬀerential decay rate of the neutron is

dλ =

(2.4G

)

8π

¯h

δ(p

+ p

)δ(m

− E

) .

We integrate over the proton momentum which eliminates the momentum-

conserving delta function

dλ =

8π

¯h



2.4G

(¯hc)





− m

− p

c − E



. (4.68)

Here, we have neglected the recoil of the proton, i.e. E

∼ m

.Themo-

menta p

and p

can have all values compatible with energy conservation.

We now use spherical coordinates

= p

dΩ

= p

dΩ

, (4.69)

where the angles refer to the direction of the electron and neutrino momenta.

The integration over angles is straightforward and it gives a factor (4π)

Integration over the neutrino momentum eliminates the ﬁnal delta function

and introduces a factor p

=((m

+ m

− E

)

. We therefore obtain

dλ =

¯h



2.4G

(¯hc)



((m

− m

− E)



− m

E dE (4.70)

where E is the electron energy.

The energy distribution of the electron is then

dλ

∝ E((m

− m

− E)



− m

(4.71)

which reproduces the experimental data as shown in Fig. 4.9.

It is the existence of such an energy spectrum which led Pauli in 1930

to the idea of the neutrino. Indeed, the β decays could not be two-body

decays into, e.g. p e

−

, otherwise the electron would be mono-energetic. A

third particle had to be present in the ﬁnal state in order to account for the

energy balance. This idea was taken up and formalized by Fermi.

The neutron lifetime is obtained by calculating the integral (4.70). the

result is

λ =

2π

¯h



2.4G

(¯hc)



)

198 4. Nuclear decays and fundamental interactions

background

beta spectrum

electron kinetic energy (keV)

200 400

600

800

−

neutrons

ill

ators

polarizing foil

Fig. 4.9. Measurement of the energy spectrum of electrons from neutron β-decay,

n → pe

−

. The top ﬁgure shows the apparatus of [41]. Cold neutrons for the

Institut Laue-Langevin nuclear reactor enter the apparatus from the left (see Fig.

3.29). The neutrons pass through a magnetized foil that reﬂect neutrons with spin

aligned in the direction of the magnetization. The polarized neutrons then enter

a region containing a magnetic ﬁeld where a certain fraction decay. The decay

electrons spiral in the ﬁeld until stopping in a plastic scintillator. The light output

of the scintillator gives a measurement of the electron kinetic energy. Spectrum

of the measured electron kinetic energy is shown in the bottom panel. The curve

shows the theoretical spectrum.

4.3 Weak interactions 199



(2x

− 9x

− 8)



− 1+x log(x +



− 1



(4.72)

x =(m

− m

)/m

(4.73)

this gives a lifetime in agreement with the experimental lifetime τ

exp

886.7 ± 1.9 s. The good agreement should not be considered a triumph: the

factor 2.4 was, in fact, derived from the neutron lifetime.

The neutron lifetime is best most accurately measured with ultra-cold

neutrons [42] as illustrated in Fig. 3.29. The ultra-cold neutrons are stored

in a box for a time T after which they are released through a shutter into a

pipe that leads them to a neutron counter. The count rate as a function of

storage time allows one to deduce the neutron lifetime after small corrections

for absorption losses on the walls of the containing vessels.

We notice that a quick order of magnitude of (4.70) can be obtained by

neglecting m

compared to ∆m = m

−m

(a rather crude approximation).

One then obtains

λ 

¯h



2.4G

(¯hc)





max

(∆mc − p)

dp (4.74)

with p

max



∆m

− m

. By replacing in this expression ∆mc by p

max

we obtain

λ ∼

15π

¯h

max



2.4G

(¯hc)



i.e. τ ∼ 951 s. (4.75)

The interesting thing about this approximate formula is to show that it is

thevolumeofphasespaceandtheﬁfth power of the maximum momentum of

the electron which is the decisive factor. This is a direct consequence of the

dimensionality of the Fermi constant.

Our simple treatment has lead to a transition matrix T (4.67) that is

“democratic,” i.e. it is independent of the ﬁnal state as long a momentum

and energy are conserved. More realistic Hamiltonians introduce non-trivial

dynamics that induce correlations between particles.

The ﬁrst complication that we would like to introduce is by taking into

account the spins of the particles. A non-relativistic neutron is described by

two wavefunctions

|n =



(r)

−n

(r)



, (4.76)

and

n| =



∗

(r) ,ψ

∗

−n

(r)



, (4.77)

where ψ

(r)andψ

−n

(r) gives the amplitude to ﬁnd the neutron at r with

spin up or down. The analogous deﬁnitions hold for non-relativistic protons,

electrons and neutrinos.

200 4. Nuclear decays and fundamental interactions

It turns out that the Hamiltonian appropriate for neutron β-decay in

the (unrealistic) limit where all participating particles are non-relativistic is

approximately

pe

−

|n =





p|I|ne|I|

 +g

p|σ|n·e

|σ|





, (4.78)

where I is the unit matrix and σ are the Pauli spin matrices. The constant

∼ 1.25 has a value that can be derived in principle from the underlying

theory of quark decay. In practice, it is ﬁxed empirically by the value of the

neutron lifetime. The transposed spinor for the electron is

e

| =



∗

−e

(r) ,ψ

∗

(r)



. (4.79)

The matrix element (4.78) contains no surprises. It is the sum of four

terms. The ﬁrst two, I ·I and σ

, yield a proton with the same spin as the

neutron and opposite spins for the e

−

and

.Thelasttwo,σ

and σ

ﬂip the nucleon spin and yield e

−

and

with the same spin. We see that

all four terms guarantee angular momentum conservation in the zero-velocity

limit for all particles where there is no orbital angular momentum. In fact,

the conservation of angular momentum is forced by the rotational invariance

of each term, II and the scalar product σ · σ.

While the non-relativistic limit (4.78) gives no new physics, the relativis-

tic generalization does. Such matrix elements use 4-component Dirac spinors

rather than 2-component Pauli spinors to describe the two spin states of par-

ticles in addition to the two spin states of their antiparticles. The formalism

has suﬃcient ﬂexibility to reproduce the following correlations observed in

β-decay:

• The directions of the e

−

and

momenta are correlated. For an angle

θ between the two momenta, the distribution of cos θ is proportional to

1+a cos θ where a =(1+g

)/(1 + 3g

) ∼ 0.5.

• A correlation of the same form exists between the spin of the neutron and

the direction of the e

−

and

momenta. The measured correlation for elec-

trons is shown in Fig. 4.10. We see that of order 5% more electrons are

emitted in the direction of the neutron spin than opposed to the neutron

spin. This is of profound importance because in indicates that parity con-

servation is violated in β-decay since the correlation would be opposite if

the experiment were observed in a mirror (Fig. 4.10).

• The

is always emitted with its spin aligned with its momentum, i.e. it

has positive helicity:

p · s

|p|

=+¯h/2(

) (4.80)