Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology

Подождите немного. Документ загружается.

150 3. Nuclear reactions

q / ( h / r )

010

r / r

−4

log |F|

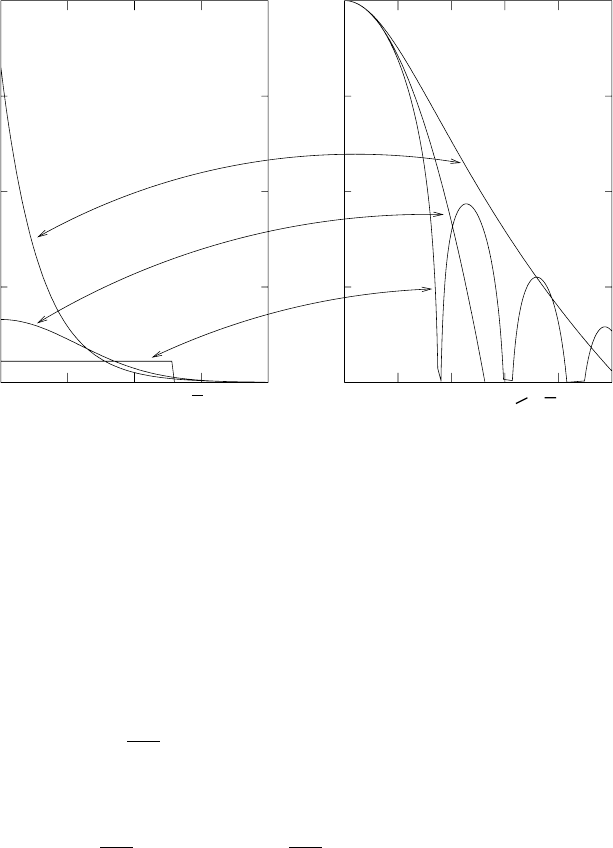
Fig. 3.19. Three charge distributions, exponential, Gaussian, and square (i.e. con-

stant within r ≤ ¯r and zero otherwise), and their form factors. The three distri-

butions shown on the left all have the same total charge, 4π



ρ(r)dr = 1 and

the same mean square radius r

 =4π



ρ(r)dr.with¯r ≡r



1/2

. The equal-

ity of their r

 requires that at low q

their form factors, on the right are all

equal, F ∼ 1 − (1/6)q

r

/¯h

. Only for q

> 4¯h

/r

 do the form factors diﬀer

signiﬁcantly.

(r)=



|ψ

,...,r

= r,r

...d

i−1

i+1

...d

is the probability density to ﬁnd the particle i inthevolumed

r at r,and

(r), deﬁned by

(r)=Z

√

α¯hcP

(r) , (3.150)

is the contribution of the charge i to the total charge density ρ(r)ofthe

bound state

ρ(r)=

√

α¯hc



i=1

(r)=

√

α¯hc˜ρ(r) (3.151)

with



˜ρ(r)d

r =



i=1

= Z

tot

(3.152)

where Z

tot

is the total charge of the system.

In these conditions, the cross-section is

3.4 Particle–particle scattering 151

dσ

dΩ

dσ

Ruth

dΩ

(Zα¯hc)|F

tot

(q)|

, (3.153)

where

dσ

Ruth

dΩ

(Zα¯hc) is the Rutherford cross-section and

tot

(q)=



iq·R/¯h

˜ρ(r)d

r (3.154)

is the Fourier transform of the charge density (divided by e). Clearly

tot

(0) = Z

tot

(3.155)

so for small momentum transfer (3.153) is reduced to the Rutherford cross-

section of a particle of charge Z on a point particle of charge Z

tot

e.Onesays

that at low momentum transfer, there is coherent scattering on the bound

state. The cross-section is proportional to the total charge (Z

tot

)

of the

composite system.

3.4.4 Electron–nucleus scattering

The nucleus is not a point particle so we can expect the elastic scatter-

ing will be suppressed for momentum transfers greater than ¯h/R where

R ∼ 1.2A

1/3

fm is the radius of the nucleus. The most eﬃcient way to see this

eﬀect is in electron–nucleus scattering. Electrons are insensitive to the nuclear

force so the elementary cross-section (the Mott cross-section, the relativistic

generalization of the Rutherford cross-section) is known very precisely and

the deviations at large scattering angle can give information of the charge

distribution, i.e. the distribution of protons in the nucleus. For relativistic

electrons E = pc, the non-vanishing size causes deviations from the Ruther-

ford cross section for

θ>

¯hc

∼

200 MeV

−1/3

, (3.156)

where we use the small angle approximation q = pθ. For electrons of energy

E = 400 MeV scattering on calcium, A

1/3

∼ 4 so we expect a suppression of

the cross-section for θ>.1, i.e. θ>7deg.

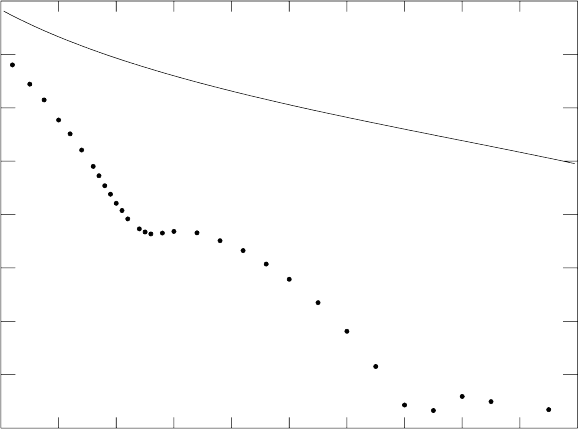
Figure 3.20 shows the cross-section as a function of angle for electrons

scattering on calcium [32]. The deviations from the Mott formula are clear and

allow one to derive the nuclear charge distribution. The oscillating pattern of

the cross-section indicates clearly that this nucleus has a relatively ﬂat charge

distribution with a relatively well-deﬁned edge (Fig. 3.19). This behavior is

seen on all nuclei with A>10 except strongly deformed nuclei where the

averaging over nuclear orientations leads to a “fuzzier” edge. Light nuclei,

A<10 have a more Gaussian charge distribution as indicated by the absence

of oscillations in their diﬀerential cross-sections.

As emphasized in Sect. 3.4.2, the scattering of an electron on a nucleus can

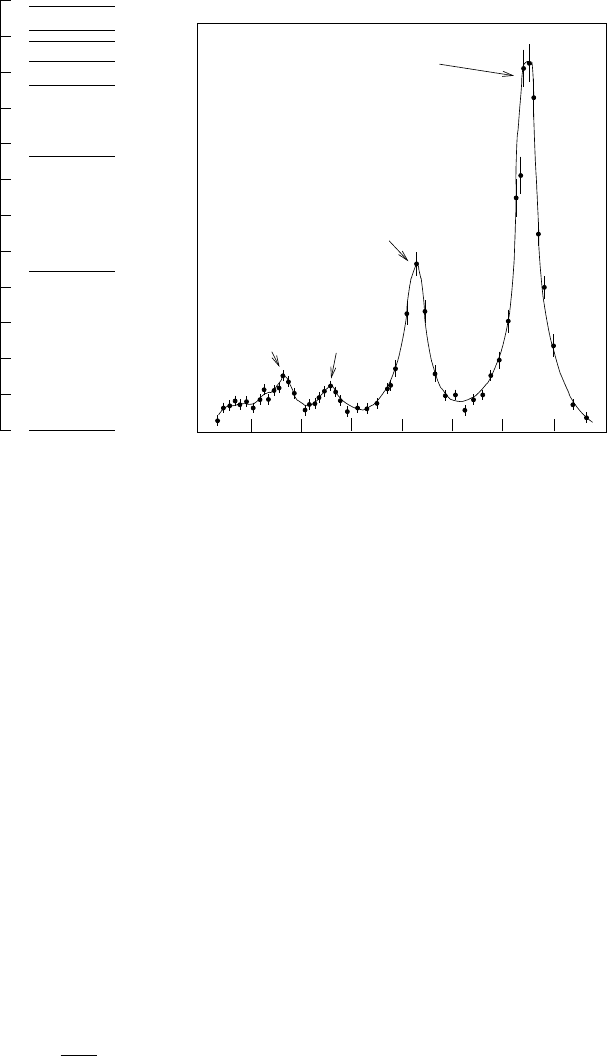
leave the nucleus in one of its discrete excited states. This is illustrated in Fig.

3.21 which shows the energy distribution distribution of electrons scattered

152 3. Nuclear reactions

−10

30 40 60 80 100

−2

(degrees)

/dσd (barn/steradian)

Ω

point nucleus

−6

−4

−8

Fig. 3.20. Elastic scattering of electrons on calcium nuclei [32]. The dashed curve

shows the Mott scattering cross-section for electrons on a heavy spinless nucleus.

at a ﬁxed angle on

C. Electrons that leave the nucleus in an excited state

must lose energy in order to conserve energy. Peaks corresponding to the

ground state (elastic scattering) and to the ﬁrst three excited states are seen.

Finally, the scattering of an electron on a nucleus can also lead to the

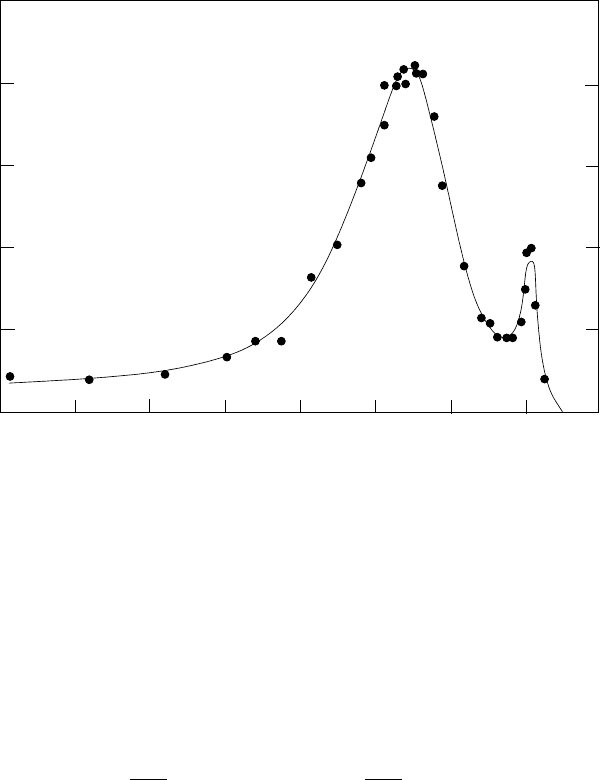
ejection of a nucleon and this is also reﬂected in the energy distribution of the

ﬁnal-state electron. This distribution is shown for electron–

H scattering in

Fig. 3.22. Their are no excited states of the deuteron so the distribution shows

two peaks, one for elastic scattering and a broader peak at lower energy for

nucleon ejection. The second peak is at lower energy because the electron loses

energy to eject a nucleon and, more importantly, the electron here scatters on

a quasi-free nucleon of smaller mass than the nucleus. The nucleon therefore

recoils with more energy than would the nucleus as a whole (Exercise 3.6).

Generally speaking, electron–nucleon scattering dominates over elastic

scattering at high q

. This is because the form-factor suppresses the elastic

cross-section at high q

and this suppression compensates the fact that the

elastic cross-section is proportional to Z

while the sum of the cross-sections

on individual nucleons if proportion only to Z. Nucleon-ejection then dom-

inates for q

greater than the value deﬁned by |F (q

−1

. From Fig.

3.19 we see that for Z ∼ 30, the required suppression by a factor ∼ 30 occurs

for q

r

/¯h

> 10, i.e. pcθ > 600 MeV.

3.4 Particle–particle scattering 153

12.

4.438

7.654

9.641

E (MeV)

172

176 180 184 18

electron energy (MeV)

Carbon

187 MeV

80 degrees

400

counts

200

100

300

9.641

7.654

ground state

4.438

Fig. 3.21. The spectrum of excited states of

C (left) and the ﬁnal-state energy

spectrum of 187 MeV electrons scattering at 80 deg on

C (right). The peak at

185 MeV corresponds to elastic scattering. (2 MeV is taken by the recoiling nucleus.)

The other peaks correspond to inelastic scattering leaving the

C nucleus in an

excited state. The three lowest excitations are clearly visible.

3.4.5 Electron–nucleon scattering

Electron scattering on nucleons is very similar to electron scattering on nu-

clei. At low values of q

one observes only elastic scattering. The angular

distribution is well described by Rutherford scattering modiﬁed by two ef-

fects:

• The nucleon and electron spins must be taken into account since they lead

to magnetic forces that modify the angular distribution.

• As in the case of nuclei, nucleons are not point particles so both the charge

and magnetic moments have spatial distributions leading to electric and

magnetic form factors.

The ﬁrst indications of the internal structure of the proton and neutron

came from the values of their magnetic moments. According to Dirac’s the-

ory, a point like elementary particle of spin 1/2 and charge q should have a

magnetic moment

e¯h

, and µ

=0 (q

=0), (3.157)

154 3. Nuclear reactions

460

420

340

380

(arbitrary units)

Ω

500 MeV 45 degrees

electron−deuteron

E’ (MeV)

Fig. 3.22. The ﬁnal-state energy spectrum of 500 MeV electrons scattering at

45 deg on

H. The peak at 460 MeV corresponds to elastic scattering. (40 MeV

is taken by the recoiling nucleus.) The broader peak at 425 MeV corresponds to

dissociation of the deuteron. This can be considered as elastic scattering of the

electron on either the proton or neutron. The peak is at lower energy because

B(2, 1) = 2.2 MeV must be provided to break the nucleus and because the recoiling

nucleon, because of its lower mass, takes more energy than a recoiling deuteron.

The width of the inelastic peak reﬂects the momentum distribution of the nucleons

in the nucleus.

i.e. a gyromagnetic ratio of γ = q/m. The observed values of the proton and

neutron moments based on magnetic resonance experiments are

=2.7928444

e¯h

= −1.91304308

e¯h

. (3.158)

These results suggests that the proton and neutron are not “elementary”

particles but have an internal structure. Today, we attribute this structure

to the quarks and gluons that form the nucleons and all other hadrons.

The conclusion based on the proton magnetic moment was conﬁrmed by

the electron–proton scattering experiments of Hofstadter. Figure 3.23 shows

the angular distribution and that expected for a structureless particle. Unlike

the case for nuclei (Fig. 3.20) no diﬀraction minima are seen. This indicates

that the proton has a more or less exponential density proﬁle, as indicated

in Fig. 3.19. Figure 3.24 shows the proton form factor deduced from the

cross-sections for the scattering of electrons of energies between 200 and 500

MeV.

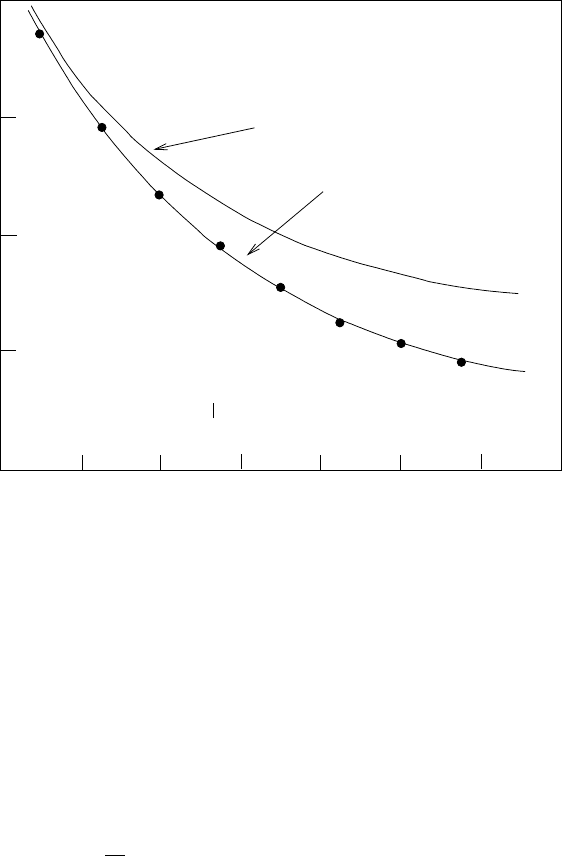
3.4 Particle–particle scattering 155

100

140

laboratory scattering angle (degrees)

−33

−32

−31

−30

−29

400 MeV

r=0

r=0.8 fm

/steradian)

Ω/d

(cm

Fig. 3.23. The measured angular distribution of 400 MeV electrons scattered from

protons. The two lines show the expected distribution for scattering from a point-

like proton and from an exponential charge distribution of mean radius 0.8fm.

The experimental points can be ﬁtted to a simple empirical charge distri-

bution:

(r)=ρ

−r/a

(3.159)

which gives a form factor

(q) = (1 + q

/¯h

)

−2

(3.160)

where a

is the mean square (charge) radius of the proton

a =(r

)

1/2

√

12a

. (3.161)

Theresultsgivea ∼ 0.8 fm which can be taken as a deﬁnition of the “size”

of the proton.

The determination of the neutron charge density is more diﬃcult because,

being unstable, dense targets cannot be made of neutrons. In practice, one

studies electron–deuteron scattering and subtracts oﬀ the contribution of the

protons.

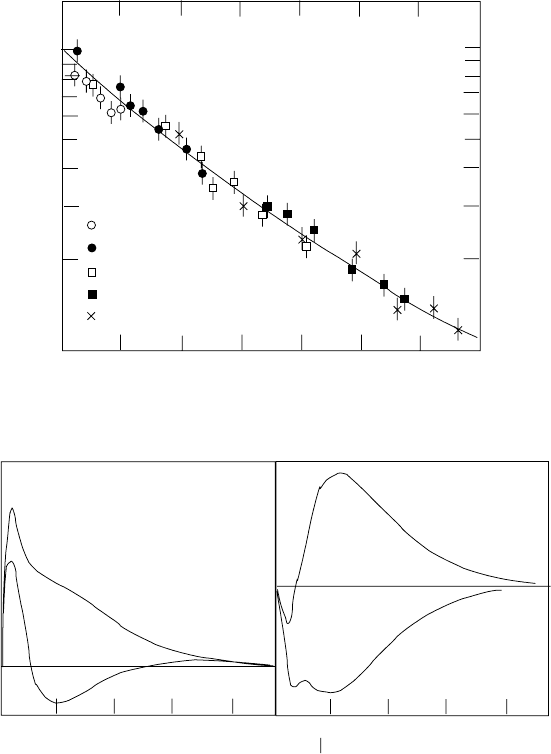
156 3. Nuclear reactions

The charge and magnetic moment densities of protons and neutrons are

shown in Fig. 3.24. We note that the neutron has a positively charged core

of radius ∼ 0.3 fm surrounded by compensating negative charge between 0.3

and 2 fm.

Charge

Magnetic

Moment

proton

neutron

proton

r (fm)

4π

/ h

(fm

−2

)

300 MeV

400 MeV

200 MeV

550 MeV

500 MeV

0.1

0.3

0.5

1.0

Fig. 3.24. Top panel: the experimental values of the proton form factor |F (q

[8]. The curve is the predicted form factor for an exponential charge distribution

with a mean charge radius of 0.8 fm. Bottom panel: the derived charge and magnetic

moment densities of the proton and neutron [33].

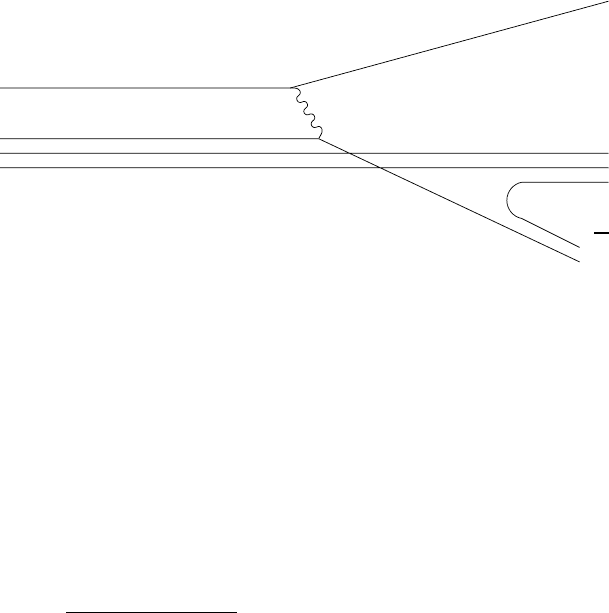
3.5 Resonances 157

Just as in electron–nucleus scattering, inelastic scattering dominates at

high q

. In electron–nucleus scattering, one see the excitation of excited nu-

clear states and scattering on individual nucleons followed by their ejection.

In electron–nucleon scattering the same sequence is seen. The excited states

of nucleons correspond to hadronic resonances. The scattering on constituents

corresponds to scattering on individual quarks. The momentum distribution

of quarks in the nucleon can be deduced from the energy distribution of scat-

tered electrons just as the momentum distribution of nucleons in nuclei can

be deduced (Fig. 3.22).

The diﬀerence from electron–nucleus scattering is that while nucleons can

be ejected from nuclei and observed, individual quarks are never observed in

ﬁnal states. Rather, one sees events with a multitude of hadrons in addition

to a nucleon. The situation is visualized in Fig. 3.25. When the struck quark

leaves the nucleon, a quark–antiquark pair is produced which recombines with

the spectator quarks so that the ﬁnal state consists of a nucleon and a pion.

The historical sequence of seeing ever more fundamental particles seems to

be broken since the fundamental particle in this case is not observed.

Fig. 3.25. Electron–proton “deep-inelastic scattering.” The proton is a bound state

uud of three quarks. The electron scatters on an individual quark by exchange of a

virtual photon. As the quark leaves the proton, a quark–antiquark pair is created.

The pair recombines with the initial quarks to make a ﬁnal state proton (uud) and

(u¯u).

3.5 Resonances

It is common, especially at low energy, for cross-sections to exhibit resonant

behavior with energy dependences of the form

σ ∼

(E − E

)

+(Γ/2)

, (3.162)

158 3. Nuclear reactions

where E

and Γ/2 are the energy and width (at half-maximum) of the reso-

nance. In nuclear physics, these resonances are excited states of nuclei that

decay rapidly (Γ =¯h/τ ) by dissociation or photon-emission. An example is

the fourth excited state of

Li (Fig. 3.5) that leads to a resonance in the

n −

Li cross-section (Fig. 3.4). More spectacular examples are the multitude

of highly excited states of heavy nuclei that have suﬃcient energies to decay

by dissociation. The cases of

236

Uand

239

U are shown in Fig. 3.26 where

these states appear as resonances in the scattering of neutrons on

235

Uand

238

U. At the hadronic level, almost all the “elementary particles” discovered

in the 60’s were resonances seen, not as tracks, but simply as maxima in

cross-sections or in invariant-mass distributions.

In order to see how resonances come about in quantum mechanics, we

examine a simple model due to Wigner and Weisskopf. Consider a discrete

state |a of energy E

and a set of continuum states |α. The discrete state

is coupled to the continuum by a Hamiltonian, H with matrix elements

a|H|α = α|H|a

∗

= H(α) (3.163)

and

a|H|a = α|H|α =0 . (3.164)

Becauseofthiscoupling,thestate|a is unstable with a lifetime given by the

Fermi golden rule (C.15)

2π

¯h

|H(α ; E

= E

) (3.165)

where ρ

) is the number of states |α perenergyintervalevaluatedat

= E

We now calculate the evolution of a system that is initially in a continuum

state |α. The most general evolution is

|ψ(t) = γ

(t)e

−iE

t/¯h

|a +



(t)e

−iE

t/¯h

|β . (3.166)

We deﬁne

=(E

− E

)/¯h, (3.167)

The Schr¨odinger equation is now two equations

i¯h ˙γ



(t)e

iω

H(β) (3.168)

and

i¯h ˙γ

= γ

(t)e

−iω

∗

(β) . (3.169)

The initial conditions are

(t =0)=0,γ

= δ

αβ

⇐⇒ | ψ(0) = |α . (3.170)

3.5 Resonances 159

Integrating (3.169) we get

(t)=δ

αβ

i¯h





−iω



∗

(β) . (3.171)

Substituting this into (3.168) we get

i¯h ˙γ

iω

H(α)+

i¯h



|H(β)|



iω

(t−t



)



)dt



. (3.172)

The Wigner–Weisskopf approximation is to replace γ



) in the integral

by γ(t). This can be justiﬁed a posteriori.Ifthisisdone,theintegralcanbe

evaluated exactly. The sum then yields the inverse lifetime of the state (as

we will see in Chap. 4). We then have

˙γ

(t)=

i¯h

iω

H(α) −

(t)

2τ

, (3.173)

τ is deﬁned by (3.165).

We can now integrate this equation to ﬁnd

(t)=

H(α)[e

i(E

−E

)t/¯h

− e

−t/2τ

]

− E

)+iΓ/2

(3.174)

with

Γ =¯h/τ . (3.175)

For t  τ this becomes

(t) 

H(α)e

i(E

−E

)t/¯h

− E

)+iΓ/2

(3.176)

giving a steady-state probability to ﬁnd the system in the state |a

P (a)=

|H(α)|

− E

)

+ Γ

. (3.177)

Supposing that |H(α)|

is a slowly varying function of the energy E

,this

probability has a peak of width Γ centered at E

Substituting (3.176) into (3.171 we ﬁnd

(t)=δ

αβ

i¯h

H(α)H

∗

(β)

− E

)+iΓ/2



i(E

−E



/¯h



. (3.178)

For β = α this is

(t)=

2π

H(α)H

∗

(β)

− E

)+iΓ/2

i(E

−E

)t/2¯h

∆

− E

) . (3.179)

The transition probability per unit time is then

To simplify things, we neglect the principal value in the integral. This corresponds

to the energy-shift of the level in second order perturbation theory.