Basdevant J.-L., Rich J., Spiro M. Fundamentals in Nuclear Physics: From Nuclear Structure to Cosmology
Подождите немного. Документ загружается.


140 3. Nuclear reactions
σ
x
σ
p
x
= σ
y
σ
p
y
= σ
z
σ
p
z
∼ ¯h. Including higher-order terms in the expansion
(3.100) leads to spreading of the wave packet at large times.
The scattered wavefunction has a similar structure:
ψ
sc
(r, θ, t)=
f(θ)
r
e
i(k
0
r−ω
0
t)
d
3
kφ(k)e
i(k
z
−k
0
)(r−v
0
t)
(3.103)
wherewehavedroppedafactorexp(i(k
2
x
+ k
2
y
)r/k
0
) which is near unity for a
sufficiently wide wave packet. We have also taken f (θ) out of the integral since
φ(k) is strongly peaked around k
0
and therefore (3.98) is well approximated
by
cos θ ∼
k
0
· r
|k
0
||r|
. (3.104)
Comparing (3.102) and (3.103), we see that
|ψ
sc
(r − v
0
t, θ, t)|
2
=
|f(θ)|
2
r
2
|ψ
in
(x = y =0,z = r − v
0
t)|
2
. (3.105)
This tells us the scattered wavefunction is simply a replica of ψ
in
that is scaled
down by a factor f(θ)/r. Note also that (3.105) implies that the scattered
wave vanishes for t 0 since it is proportional to the incident wave at
(t 0,z 0) which vanishes.
Substituting (3.105) into (3.94) we find the required identification of the
differential scattering cross-section and the square of the scattering amplitude
(3.99).
We now need to find the relation between f(θ) and the potential V (r).
This is easy to do if the potential is sufficiently weak that the wave packet
is only slightly perturbed as it passes through the potential. We rewrite the
eigenvalue equation (3.95) as
(∇
2
− k
2
)ψ
k
(r)=2mV (r)ψ
k
(r)/¯h
2
(3.106)
where k =
√
2mE/¯h. We will look for solutions of the form
ψ
k
=e
ikz
+ ψ
k sc
, (3.107)
where the first term is a solution of the eigenvalue equation with V =0
and the second term is a particular solution to the equation with V =0.
Since the effect of the potential is assumed to be small, it should be a good
approximation to replace the wavefunction of the right-hand side of (3.106)
with the incident plane wave:
(∇
2
− k
2
)ψ
k
(r)=4πS(r) , (3.108)
where
S(r)=
2mV (r) exp(ik · r)
4π¯h
. (3.109)
For k = 0 this is the Poisson equation of electrostatics with the electrostatic
potential replaced by ψ
k
(r) and the charge density replaced by S(r). The
solution is well-known:

3.3 Quantum mechanical scattering on a fixed potential 141
ψ
k sc
(r)=
1
4π
d
3
r
1
|r − r
|
S(r
)(k =0). (3.110)
For k = 0, the solution is only slightly more complicated:
ψ
k sc
(r)=
1
4π
d
3
r
exp(ik|r − r
|)
|r − r
|
S(r
) . (3.111)
This formula has a simple physical interpretation: the scattered wave is a
sum of spherical waves generated at each point r
in the potential well and
having an amplitude proportional to S(r
) ∝ V (r
).
Equation (3.111) can be written as
ψ
k sc
(r)=
2m
4π¯h
2
d
3
r
exp(ik|r − r
|) exp(ikz
)
|r − r
|
V (r) . (3.112)
We are interested in ψ
sc
far from the scattering center in which case we
can approximate r
= 0 (in the denominator) and |r − r
|∼r − r · r
/r
(in the numerator). A particle observed at r will be interpreted as having
a momentum p
= p
0
r/r implying |r − r
|∼r − k
· r
/k
0
so the scattered
wavefunction is
ψ
k
(r)=
2me
ikr
4πr
d
3
r
V (r
) exp(iq · r
/¯h) , (3.113)
where q = p−p
is the momentum transfer of magnitude |q|
2
=2p
2
0
(1−cos θ).
We see that the scattered wave is proportional to the Fourier transform of
the potential.
˜
V (q)=
e
iq·r/¯h
V (r)d
3
r . (3.114)
The differential cross section is then
dσ
dΩ
=
m
2
4π
2
¯h
4
|
˜
V (p − p
)|
2
(3.115)
as found in the previous section.
Equation, (3.115) tells us that the cross-section takes an especially simple
form if q =0
dσ
dΩ
(q =0) =
m
2
4π
2
¯h
4
V (r)d
3
r
2
. (3.116)
Since q
2
=2p
2
(1−cos θ), this condition is met either in the forward direction,
θ = 0, or in the low-energy limit where the de Broglie wavelength is much
greater than the range of the potential, ¯h/p R.Forq
2
=0,theexponential
in the integrand is an oscillating function of r
so the integral is suppressed.
This can be intuitively understood by saying that far from the region where
V = 0, the spherical waves generated at different positions are not entirely
in phase and therefore partially cancel. As seen in (3.112) and in Fig. 3.15,
only for θ =0orfor¯h/p R is the phase independent of r
so the spherical
waves are entirely in phase at the observer’s position r.

142 3. Nuclear reactions
v= o
k
r
r
r−r
θ
o
Fig. 3.16. A wave packet of central momentum p
0
=¯hk
0
that impinges upon
a region with V (r) = 0. The scattered wave packet at r is the superposition of
spherical waves generated at each point r
. A particle observed at r will be inter-
preted as having a momentum p
= p
0
r/r implying a momentum transfer squared
of |q|
2
= |p
− p|
2
=2p
2
0
(1 − cos θ).
The suppression of the cross-section for θ = 0 because of destructive
interference is quite different from the classical case. Here, the large angle
cross-section is suppressed simply because the particle trajectory must pass
near the center of the potential in order to produce a wide-angle scatter.
While the decline of the cross-section with increasing scattering angle
has different origins in quantum and classical mechanics, we saw previously
that the classical and quantum calculations may give identical answers as
long as q
2
= 0. In fact, what distinguishes quantum scattering from classical
scattering is that in quantum scattering the cross-section must be isotropic
for qR 1. This condition is met at all scattering angles if the de Broglie
wavelength of the incident particle is much greater than the range R of the
potential. This is equivalent to the condition
p
2
2m
<
(¯hc)
2
8R
2
mc
2
= 5 MeV
1GeV
mc
2
1fm
R
2
. (3.117)
For incident energies below this limit, the scattering must be isotropic. For
incident energies above this limit, the scattering will still be isotropic at small
angles:

3.4 Particle–particle scattering 143
θ<
¯hc
2(p
2
/2m)mc
2
R
=2
5MeV
p
2
/2m
1/2
1GeV
mc
2
1/2
1fm
R
,(3.118)
where we have taken the small-angle limit (1−cos θ)=θ
2
/2. For angles larger
than this values, the cross-section decreases, as seen in Fig. 3.6.
3.4 Particle–particle scattering
We now return to the treatment of scattering using time-dependent perturba-
tion theory as in Sect. 3.3.2. In this section, we complicate slightly the scat-
tering problem by taking into account the recoil of the target particle. The
immediate result will be that the translation invariance of the Hamiltonian
enforces momentum conservation, a fact that was ignored in fixed-potential
scattering.
3.4.1 Scattering of two free particles
We consider now the scattering to two particles, 1 and 2, with initial momenta
p
1
and p
2
, and final momenta p
1
and p
2
.Wetakethepotentialenergytobe
V (r
1
−r
2
), i.e. a function only of the relative coordinates of the two particles.
The conservation of momentum will be a consequence of the assumption that
the interaction potential V (r
1
− r
2
) is translation invariant.
d Ω
p
p’
1
2
1
p’
Fig. 3.17. Scattering of two particles with recoil.
The treatment of this problem follows the treatment of scattering on fixed
potential starting with the transition rate given by (3.56). The initial and final
state wavefunctions are now
ψ
i
(r
1
,r
2
)=
e
ip
1
·r
1
L
3/2
e
ip
2
·r
2
L
3/2
ψ
f
(r
1
,r
2
)=
e
ip
1
·r
1
L
3/2
e
ip
2
·r
2
L
3/2
. (3.119)

144 3. Nuclear reactions
The matrix element between initial and final states is
f|V |i =
1
L
6
e
i(p
1
−p
1
)·r
1
/¯h
e
i(p
2
−p
2
)·r
2
/¯h
V (r
1
− r
2
)d
3
r
1
d
3
r
2
=
1
L
6
e
i(p
1
−p
1
)·(r
1
−r
2
)/¯h
e
i(p
1
+p
2
−p
1
−p
2
)·r
2
/¯h
V (r
1
− r
2
)d
3
r
1
d
3
r
2
.
Replacing the integration variable r
1
by r = r
1
− r
2
, we find
f|V |i =
˜
V (p
1
− p
1
)
L
6
(2π¯h)
3
∆
3
L
(p
1
+ p
2
− p
1
− p
2
) , (3.120)
where
∆
3
L
(p)=
i=x,y,z
1
π
sin p
i
L/2¯h
p
i
(3.121)
is a limiting form of the three-dimensional delta function (see Appendix
C.0.2). The matrix element is the product of the Fourier transform of the
potential introduced previously and an oscillating function (3.121) whose
role, when squared, is to force momentum conservation:
[∆
3
L
(p)]
2
=
L
3
δ
3
(p)
(2π¯h)
3
. (3.122)
Substituting into (3.56), the transition rate to the final state is
λ
i→f
=
2π
¯h
|
˜
V (p
1
− p
1
)|
2
L
12
δ(E
f
− E
i
)L
3
(2π¯h)
3
δ
3
(p
1
+ p
2
− p
1
− p
2
) .
The number of states within the momentum volume d
3
p
1
d
3
p
2
is
dN =
L
3
d
3
p
1
(2π¯h)
3
L
3
d
3
p
2
(2π¯h)
3
. (3.123)
The total transition rate into these states is then
λ(d
3
p
1
, d
3
p
2
) = (3.124)
L
2π¯h
3
d
3
p
1
d
3
p
2
2π
¯h
|
˜
V (p
1
− p
1
)|
2
L
6
δ(E
− E)δ
3
(p
1
+ p
2
− p
1
− p
2
) .
Integrating over d
3
p
2
,wefindthetransitionrate
λ(d
3
p
1
) = (3.125)
L
2π¯h
3
d
3
p
1
2π
¯h
|
˜
V (p
1
− p
1
)|
2
L
6
δ(E
1
+ E
2
− E
1
− E
2
) ,
where E
2
= E
2
(p
1
+ p
2
− p
1
) is determined by momentum conservation.
This is the same transition rate as in the fixed potential case (3.68) except
that the energy-conservation delta function now includes the effect of nuclear
recoil. If the nuclear recoil is negligible, the reaction rate is identical to that
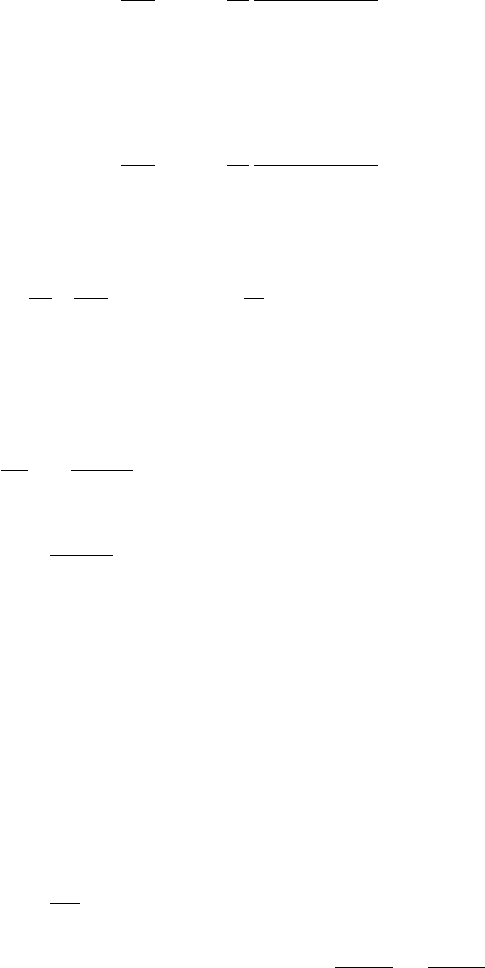
3.4 Particle–particle scattering 145
calculated for a fixed potential. In particular, for a heavy target at rest, we
have E
2
= m
2
c
2
and E
2
= m
2
c
2
+(p
2
)
2
/2m
2
and
λ(d
3
p
1
)=
L
2π¯h
3
d
3
p
1
2π
¯h
|
˜
V (p
1
− p
1
)|
2
L
6
δ(E
1
− E
1
+(p
2
)
2
/2m
2
) ,
which reduces to the fixed potential result when m
2
→∞.
Another interesting limit is the collision of two ultra-relativistic particles.
We treat the problem in the center-of-mass so that E
1
= E
2
= E
cm
/2. The
transition rate is
λ(d
3
p
1
)=
L
2π¯h
3
d
3
p
1
2π
¯h
|
˜
V (p
1
− p
1
)|
2
L
6
δ(2E
1
− 2E
1
) , (3.126)
or
λ(dΩ,dE
1
) = (3.127)
2c
L
3
1
2π¯h
3
dΩp
1
E
1
dE
1
π
¯hc
|
˜
V (p
1
− p
1
)|
2
δ(2E
1
− 2E
1
) .
Dividing by the factor 2c/L
3
gives the cross-section (where L cancels off
identically).
A simple example is high-energy neutrino–electron elastic scattering in
which case
˜
V ∝ G
F
. This gives isotropic scattering in the center-of-mass
dσ
dΩ
∝
G
2
F
E
2
cm
4π
2
, (3.128)
with a total cross-section of
σ ∝
G
2
F
E
2
cm
π
. (3.129)
The correct numerical factors are given in Table 3.1.
By taking into account the recoil of the target, we have introduced that
added constraint of momentum conservation into the cross-section. Since mo-
mentum conservation is the result of the translation invariance of the Hamil-
tonian, we can anticipate that it will hold in more general reactions between
two (or more) free particles. Consider a reaction
a
1
+ a
2
→ b
1
+ b
2
+ ...+ b
n
. (3.130)
The initial momenta are p
1
and p
2
with p = p
1
+ p
2
being the total momen-
tum and E = E
1
+E
2
the total energy. The final state momenta and energies
are q
i
,i=1,...,n and E
i
.
We can anticipate that the cross-section will be of the form
dσ =
2π
¯hv
0
G(p
1
, p
2
; q
1
,...,q
n
)(2π¯h)
3
× δ(p − Σq
i
)δ(E − ΣE
i
)
d
3
q
1
(2π¯h)
3
...
d
3
q
n
(2π¯h)
3
, (3.131)
146 3. Nuclear reactions
where G is the square of the relevant transition amplitude. This expression
only has meaning after we integrate it over four independent variables (for in-
stance one momentum and one energy) in order to remove the delta functions
coming from the conservation of energy and momentum.
Finally, we note that, in general, the relative velocity v
0
of the initial
particles is
v
0
=
(v
1
− v
2
)
2
− (v
1
∧ v
2
)
2
/c
2
1/2
(3.132)
This expression must be used if the initial particles are not collinear.
3.4.2 Scattering of a free particle on a bound particle
It is often the case that free particles are scattered on particles that are not
free but rather bound in potential wells as illustrated in Fig. 3.18. Consider
a particle a of mass m
a
that can scatter on a particle b of mass m
b
that is
bound near the origin by a potential U(r
b
) (acting only on particle b). The
interaction between a and b is described by another potential V (r
a
− r
b
).
The possible wavefunctions of b in the potential U are called {ψ
n
(r
b
)}.
ε
0
ε
n
p’
ε
0
ε
n
p’
p’
b
p
a
a
a
a
p
Fig. 3.18. Scattering of particle a on particle b in a bound state. Particle b can be
left in bound state (left) or ejected from the potential (right).
An example of such a process is the scattering of electrons on deuterons.
The deuteron is a bound state of a proton and neutron interacting through
the nucleon–nucleon potential. The electron interacts with the proton via the
Coulomb potential. Another example is ν
e
-deuteron scattering. In this case
the ν
e
interacts with the neutron, i.e. ν
e
n → e
−
p.
We assume that initially b is in its ground state ψ
0
(r
b
). The initial state
wavefunction is then the product of a plane wave and a bound-state wave-
function, L
−3/2
e
ip·r/¯h
ψ
0
(r
b
). In the final state, b caneitherstayinitsground
state or be placed in an excited state ψ
n
(r
b
):
|f→L
−3/2
e
ip
·r/¯h
ψ
n
(r
b
) . (3.133)
Energy conservation implies
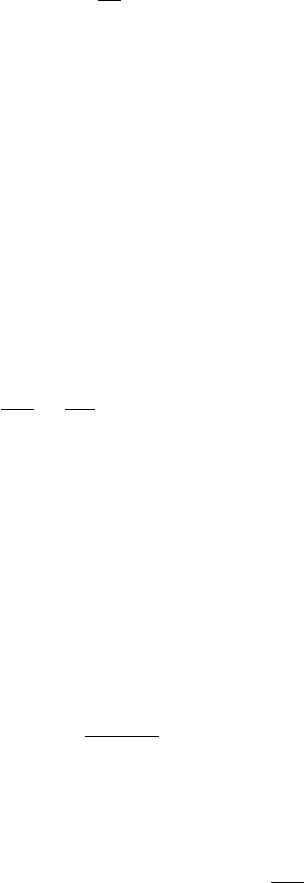
3.4 Particle–particle scattering 147
E(p
)=E(p) − (ε
n
− ε
0
) . (3.134)
In the Born approximation, the scattering matrix element is
f|T |i =
1
L
3
e
i(p−p
)r/¯h
ψ
∗
n
(r
b
)ψ
0
(r
b
)V (r − r
b
)d
3
rd
3
r
b
. (3.135)
After changing integration variables (r
a
, r
b
) → (r
a
− r
b
, r
b
) this becomes
f|T |i = L
−3
˜
V (p − p
) F
n
(p − p
) (3.136)
where
˜
V is the previously defined Fourier transform
˜
V (q)=
e
iq·r/¯h
V (r)d
3
r (3.137)
and where F
n
is defined as
F
n
(q)=
e
iq·r
b
/¯h
ψ
∗
n
(r
b
)ψ
0
(r
b
)d
3
r
b
. (3.138)
The amplitude is then the product of the Fourier transforms of the potential
V (r
a
− r
b
) and the Fourier transform of the product of the initial and final
state wavefunctions of b. This leads to a factorization of the cross-section for
the excitation of the final state n:
dσ
n
dΩ
=
dσ
f
dΩ
|F
n
(p − p
)|
2
(3.139)
where dσ
f
/dΩ is the cross-section on a free particle b. It is given by (3.72) for
elastic scattering (n = 0) and, in general, by (3.86). The function |F
n
(p−p
)|
2
is called the form factor for excitation of the state n.
The target particle can also be ejected from its potential well into a free
state of momentum p
b
. In this case, the final state is
|f→e
ip
·r/¯h
e
ip
1
·r
b
/¯h
/L
3
. (3.140)
Energy conservation now implies
E(p
)+E(p
b
)=E(p)+ε
0
. (3.141)
We introduce the Fourier transform of the initial wavefunction:
˜
ψ
0
(p
b
)=
1
(2π¯h)
3/2
e
−ip
b
.r
b
/¯h
ψ
0
(r
b
)d
3
r
b
, (3.142)
which gives the amplitude for the initial bound particle to have a momen-
tum p
b
. We then obtain, after a straightforward calculation, the scattering
amplitude
p
b
p
|T |p = L
−3
˜
V (p − p
)
2π¯h
L
3/2
˜
ψ
0
(p
b
= p
+ p
b
− p) . (3.143)
We see that the scattering amplitude is a product of the amplitude for scat-
tering on free particle, p → p
, and the amplitude for the initial bound

148 3. Nuclear reactions
particle to have the correct momentum to give momentum conservation. The
cross-section for dissociation then factorizes:
dσ
d
3
p
d
3
p
b
=
dσ
d
3
p
(pp
b
→ p
p
b
) |
˜
ψ
0
(p
b
)|
2
. (3.144)
In other words, the cross-section is the product of the cross-section on a free
particle of momentum p
b
times the probability |
˜
ψ
0
(p
b
)|
2
that the ejected
particle had the momentum p
b
before the collision.
The three types of scattering considered here give complementary infor-
mation on the target.
• Elastic scattering where b is left in its ground state. The form-factor is just
the Fourier transform of the square of the ground-state wavefunction
F
0
(q)=
e
iq·r/¯h
|φ
0
(r)|
2
d
3
r . (3.145)
We see that if we know the elementary cross-section, dσ
f
/dΩ,ameasure-
ment of the cross section on bound b’s yields the (modulus squared of the)
Fourier transform of the square of the ground-state wavefunction. Since
the ground-state wavefunction has no zeroes and can be taken to be real,
this can be inverted to give the wavefunction itself. We will see in the next
section how this allows us to determine the charge distribution of nuclei.
• Production of an excited state. This reaction gives information on the
wavefunction, quantum numbers and lifetime of the excited state. In fact,
the so-called Coulomb excitation of nuclear states due to the passage of a
charged particle is one of the important methods of deducing lifetimes of
low-lying states. Unfortunately, the formalism we have given here is not
general enough to completely explain this effect. It is better described as a
two-step process: the emission of a virtual photon by the incident particle
and the absorption of the photon by the target.
• Dissociation of the bound state. This reaction allows us to deduce the
momentum distribution of the target particle in its initial ground state.
We will see that this will allow us to deduce the momentum distribution
of quarks within nucleons from inelastic electron–nucleon scattering.
We note that |F
0
(q =0)|
2
= 1 and that |F
0
(q =0)|
2
< 1, i.e. that
the form factor acts to suppress the elastic cross section at large q
2
.Thisis
understandable intuitively because we saw in Sect. 3.3.5 that the decline of
the cross-section with increasing q
2
is due, in the Born approximation, to the
fact that the spherical waves emanating from different points in the region of
V = 0 will not be in phase with each other except in the forward direction. If,
in addition, the center of the potential is “smeared out” by the wavefunction
of b, the phases of the emanating waves are further randomized, leading to a
stronger decrease with q
2
.
Three examples of wavefunctions and their form factors are shown in
Table 3.2.

3.4 Particle–particle scattering 149
Table 3.2. Three squared wavefunctions and their Fourier transforms. The common
mean square radius is ¯r
2
=4π
r
4
|ψ(r)|
2
dr.
|ψ(r)|
2
F (q
2
)
¯r
−3
(3
3/2
/π)exp(−2
√
3r/¯r)(1+¯r
2
q
2
/12¯h
2
)
−2
¯r
−3
(3/2π)
3/2
exp(−3r
2
/2¯r
2
)exp(−¯r
2
q
2
/6¯h
2
)
¯r
−3
(3/5)
3/2
(3/4π) r<
5/3¯r 3α
−3
(sin α − α cos α) α =
5/3|q|¯r/¯h
0 r>
5/3¯r
Some care must be taken with regards to the validity and the generaliza-
tion of these results. For more details, see for instance Mott and Massey The
theory of atomic collisions, Chap. XII.
These results can be generalized to the case of a bound state of n particles
with a wavefunction ψ(r
1
,...,r
n
). Taking the case of elastic scattering, we
call T
i
f
the scattering amplitude on the particle i. The contribution to the
elastic amplitude of the particle i is
T
i
b
= T
i
f
F
i
0
(q) (3.146)
with q = p −p
, T
b
and T
f
are respectively the matrix elements on bound
and free particles and
F
i
0
(q)=
e
iq·r
i
/¯h
|ψ
0
(r
1
,...r
i
,...,r
n
)|
2
d
3
r
1
...d
3
r
n
. (3.147)
In the Born approximation, we can ignore multiple scattering so the total
amplitude is simply the sum
p
|T |p =
n
i=1
p
|T
i
b
|p . (3.148)
The cross section is then proportional to |p
|T |p|
2
.
3.4.3 Scattering on a charge distribution
Suppose that ψ
0
(r
1
,...r
n
)isthewavefunctionofasetofboundpointcharges
Z
1
,...Z
n
, and consider the elastic scattering of a charge Z on the bound
state. The elementary scattering amplitude is simply the Rutherford ampli-
tude that we write as
p
|T |p = ZZ
i
α¯hc
˜
T
i
(p, p
) (3.149)
by factoring out the coupling ZZ
i
α¯hc.Thequantity
