Бахтин С.А., Овчинников И.Г., Инамов Р.Р. Висячие и вантовые мосты. Проектирование, расчет, особенности конструирования
Подождите немного. Документ загружается.

71
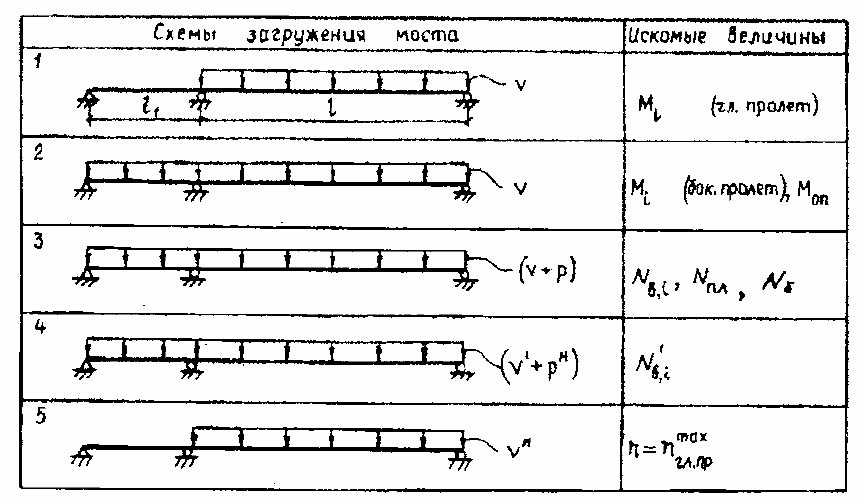
нимальный отрицательный момент над опорным сечением М
оп
;
третье загружение (v + р,
η
= l+l
1
) – максимальные усилия в вантах и
пилоне N
в, i
;
четвертое загружение (v' + р
н
,
η
= l + l
1
) – экстремальные усилия в
вантах для расчета на выносливость N'
в,i
;
пятое загружение (v
н
,
η
= l) – экстремальные величины прогибов
балки жесткости
η
i
.
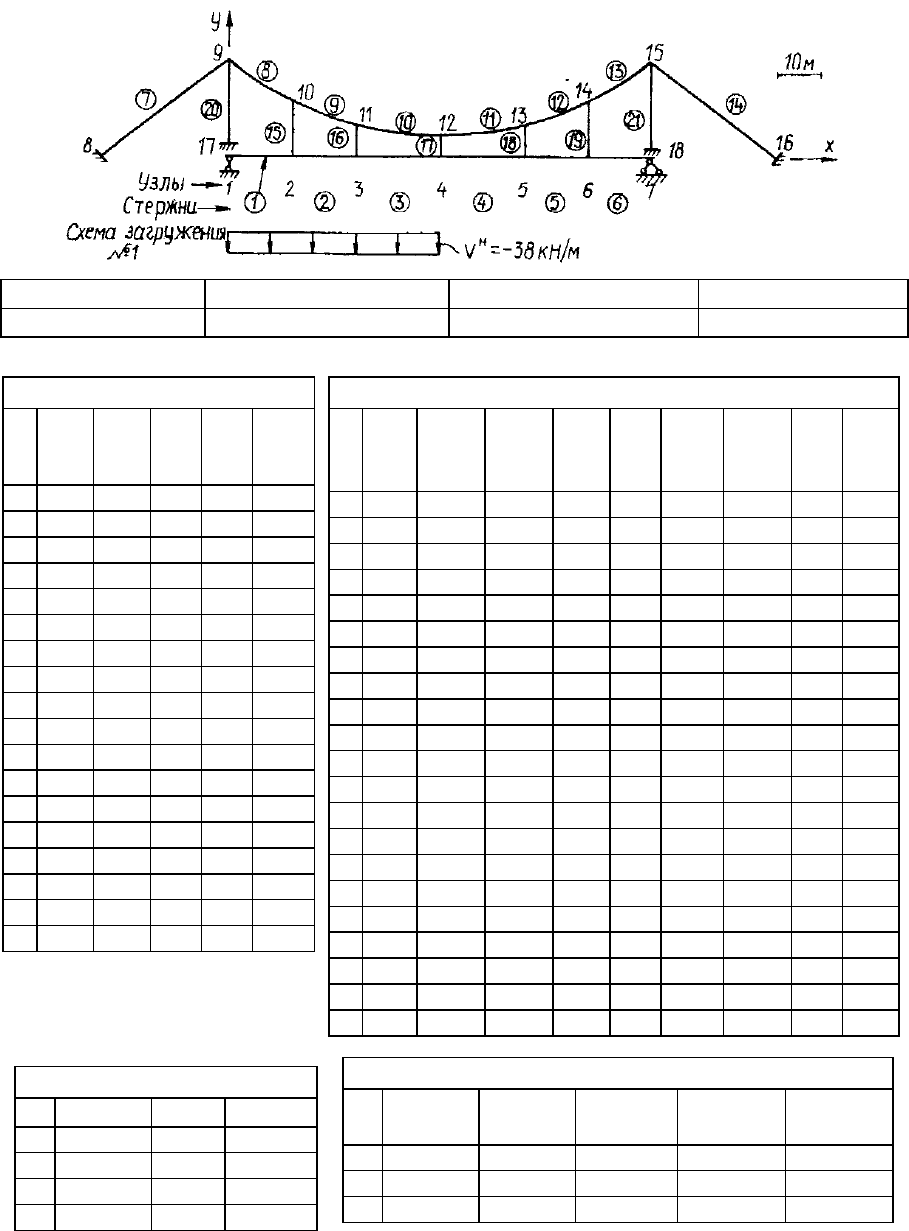
Рис. 3.22. Схемы загружения вантового моста для расчета на ЭВМ
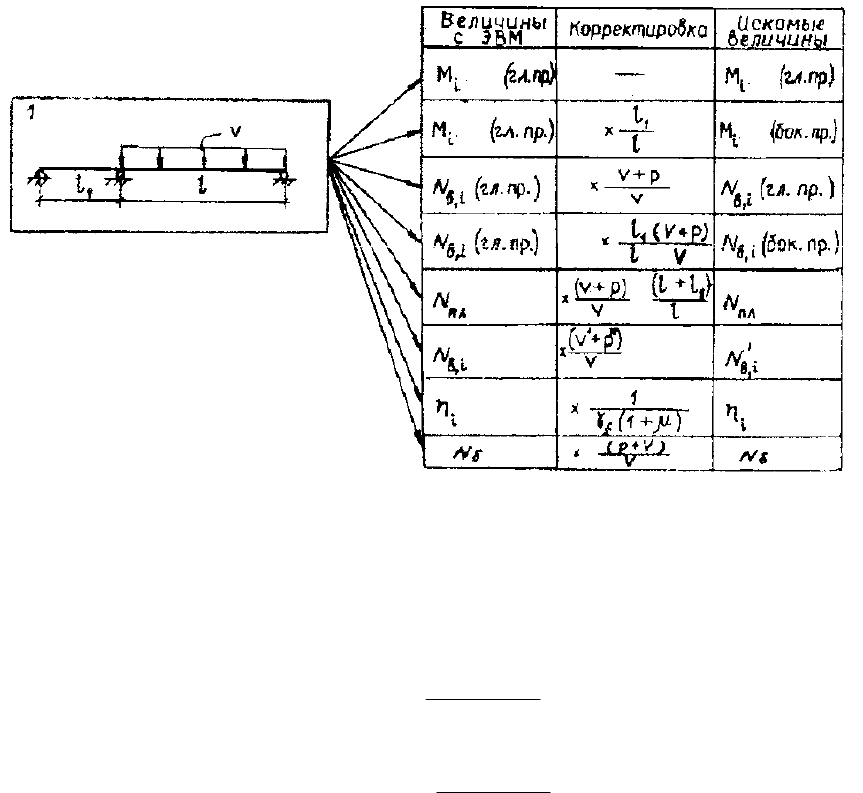
При курсовом проектировании в случае, если приходится ограничиваться
одним загружением, резонно выбрать первое загружение и получить все
искомые экстремальные усилия и прогибы путем корректировки результа-
тов с некоторым приближением (см. рис. 3.23).
Для вантовых мостов характерны относительно большие длины па-
нелей d
i
, поэтому их следует для расчета разбивать на 2-3 части.
После построения графиков (см. рис. 3.19) следует также дать оценку
жесткости пролетного строения в целом:
[
]
η
max
≤
∆
. (3.18)
Если проверка (3.18) выполняется, то проводится подбор сечения
балки и вант по прочности и выносливости по формулам (3.13), (3.14),
(3.17), но с учетом того, что значения
А
в i
ЭВМ
,
и I
б
ЭВМ
можно уменьшать
только при наличии определенного запаса по жесткости (3.18).
72
Рис. 3.23. Схема загружения вантового моста для получения
приближенных результатов
При невыполнении условия (3.18) следует увеличить изгибную же-
сткость балки
ЕI
б
и осевые жесткости вант Е
к
А
в,i
пропорционально полови-
не превышения
η
max
по сравнению с [
∆
]:
[
]
[]
II
б
т
б
ЭВМр
max
≈+
−
1
2
η∆
∆
, (3.19)
[
]
[]
АА
в i
т
в i
ЭВМ
,
р
,
max
≈+
−
1
2
η∆
∆
. (3.20)
По найденным значениям
А
в i
т
,
р
и I
б
тр
подбираются реальные сечения
(I
б
> I
б
тр
и А
в,i
> А
в i
т
,
р
), которые далее проверяются по прочности и выносли-
вости (см. п. 3.5.1). Аналогично проводится подбор сечения пилона по
формуле (3.15). Однако следует иметь в виду, что у вантовых мостов часто
используют одну плоскость вант (см. рис. 2.5) и А-образные пилоны. По-
этому нужно четко следить за тем, с какой ширины пролетного строения
собиралась нагрузка, на сколько плоскостей вант и стоек пилонов она пе-
редается.
Несколько больше отличий у вантовых мостов с железобетонной
балкой жесткости. Для металлической балки проверка прочности выполня-
ется по формуле (3.17). При этом необходимо помнить, что для вантовых
мостов, в которых проводится регулирование усилий, можно считать, что
изгибающие моменты в балке жесткости действуют только от нагрузки
v -
73
схемы № 1, 2 по рис. 3.22. Но продольные силы в балке возникают от сум-
марной нагрузки (
v + р) - схема 3, рис. 3.22, что необходимо учитывать при
подстановке величин
N
б
и М
б
в формулу (3.17).
Для железобетонной балки тоже допускается проводить проверку
прочности как для упругого тела (формула (3.17), но без коэффициентов
ψ
,
χ
, m и с заменой R
y
на R
bt
), если она подбиралась из условия обеспечения
жесткости пролетного строения (3.19) и напряжения в ней
σ
б
, значительно
меньше расчетного
R
bt
. Но если балка работает со значительными напря-
жениями
σ
б
, то ее сечение следует проверить по методике предельных со-
стояний [1], предварительно расставив арматуру.
Рассмотренный в п. 3.3 вопрос учета провисания вант под действием
собственного веса (см. рис. 3.12, д) требует итерационного процесса. Не-
обходимо выполнить несколько уточняющих перерасчетов конструкции с
изменением модуля упругости вант на каждой стадии итерации, опреде-
ляя
()
()
Np v кН азница N кН
i
i
Б6
1
4
13
94 55 34 32 56 37 7006 33 0 5=
++=⋅ +⋅ = =
=
∑
ωωω
,, ,р ,%
∆
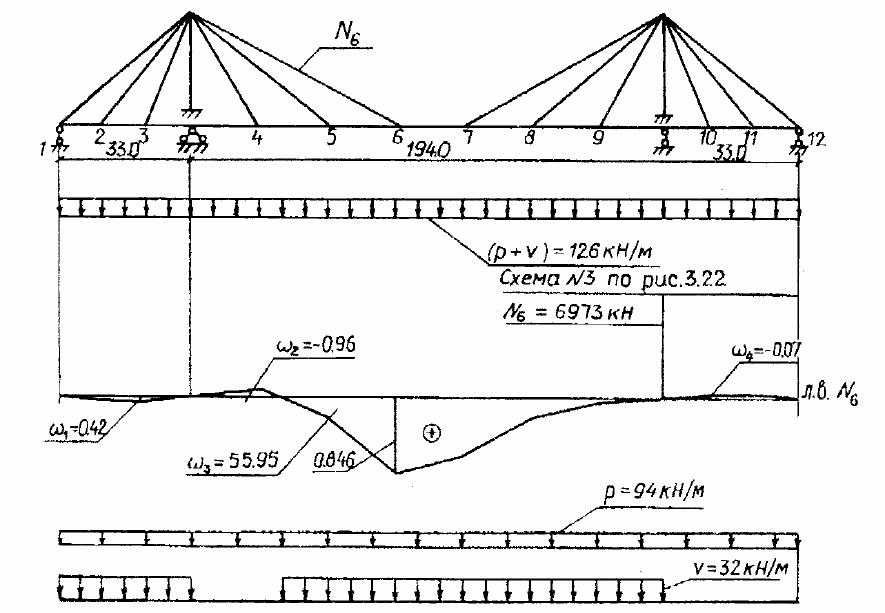
Рис. 3.24. Пример загружения вантового моста по схеме рис. 3.22 с невыгодным
положением временной нагрузки в соответствии с линией влияния
74
приведенный модуль упругости Е
ef
по формуле (195) [1].
Алгоритм загружения висячих и вантовых мостов, представленный
на рис. 3.20-3.23. для более точных расчетов, например при дипломном
проектировании, можно дополнить построением линий влияния. Совре-
менные вычислительные комплексы позволяют это сделать с минималь-
ными затратами.
Как отмечалось в пп. 3.2 и 3.3, аппарат линий влияния применим для
получения невыгодных загружений временной подвижной нагрузкой для
вантовых и висячих мостов, хотя для последних с некоторым приближени-
ем.
На рис. 3.24 показан пример уточнения схемы загружения постоян-
ной и временной нагрузками для получения экстремальных усилий в ванте
N
6
по линии влияния.
3.5.3.
Подготовка исходных данных для расчета на ЭВМ. В на-
стоящее время в учебных целях широко используется вычислительный
комплекс на основе МКЭ, разработанный в МГТУПС под руководством
проф. Н.Н. Шапошникова. Ниже приводятся рекомендации по подготовке
исходных данных применительно к данной программе, хотя они могут
быть использованы и для других вычислительных комплексов.
Прежде всего, следует учесть гибкость вант, кабеля и подвесок путем
задания их малой изгибной жесткости (
I ≈ 0,000 001 м
4
). Для исключения
проблем с размерностью все усилия рекомендуется задавать в килоньюто-
нах, геометрические размеры в метрах, а модули упругости в килоньюто-
нах на метр в квадрате (
E
s
= 2·10
8
кН/м
2
, Е
b
= 0,3·10
8
кН/м
2
).
Нумерация узлов и стержней выполняется сначала по балке жестко-
сти, потом по участкам кабеля, подвескам или вантам, пилонам, таким об-
разом, чтобы можно было для ввода исходных данных использовать сер-
висную опцию «Повторитель» (рис. 3.25, 3.26). Для висячих мостов можно
в расчетной схеме уменьшить количество подвесок для сокращения числа
узлов и стержней. При этом следует помнить, что увеличение шага подве-
сок в 2...4 раза требует при задании их жесткости в такое же число раз уве-
личить площадь их поперечного сечения.
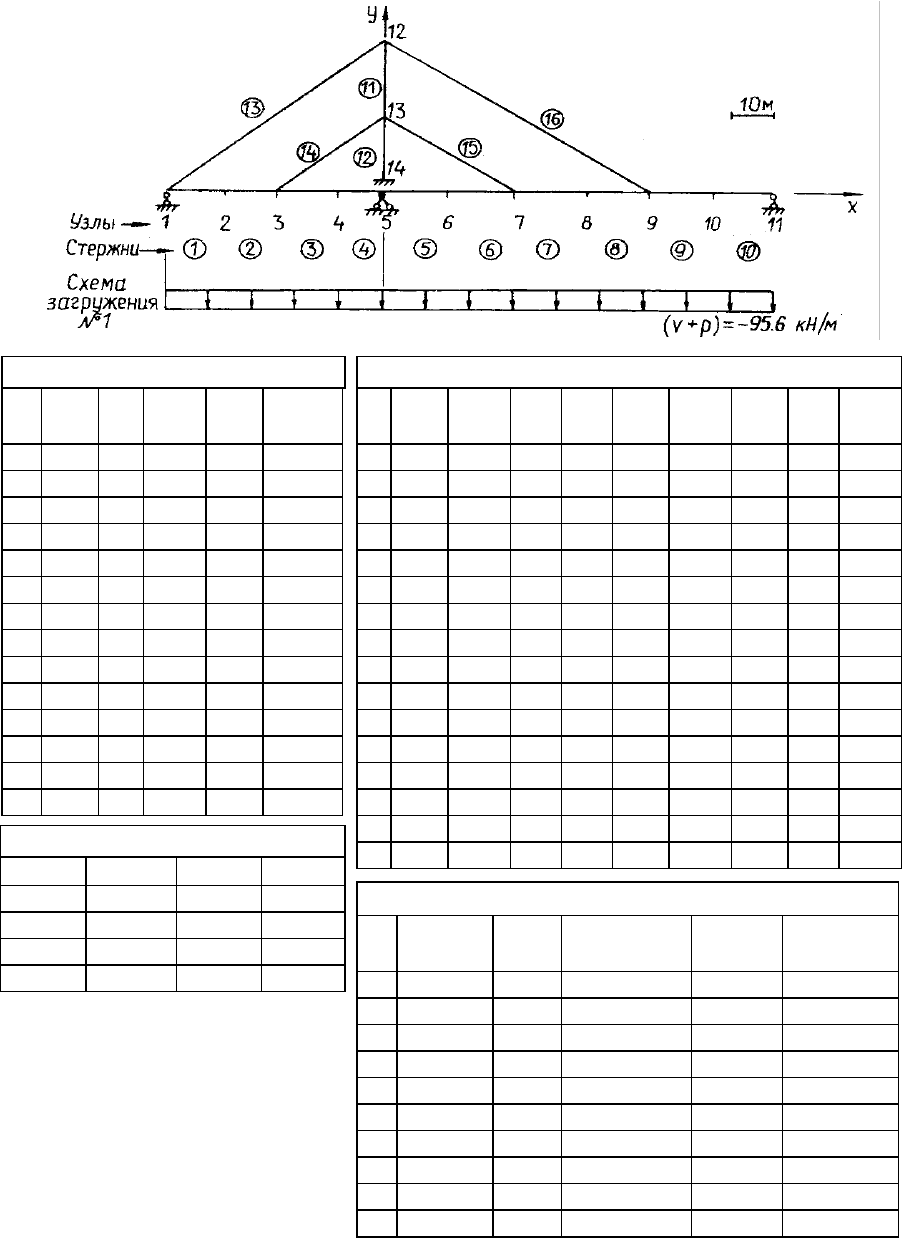
На рис. 3.25 и 3.26 приведены численные примеры подготовки ис-
ходных данных для вантового и висячего мостов. Для вантовой схемы па-
нели балки жесткости желательно разделить на 2-3 части, чтобы получить
более точное очертание эпюр внутренних усилий (см. рис. 3.25).
75
Стержни
№ на-
чало
x у шар
нир
конец
x у шар
нир
сече-
ние
1 1 -50.0 0.0 0 2 -37.5 0.0 0 1
2 2 -37.5 0.0 0 3 -25.0 0.0 0 1
3 3 -25.0 0.0 0 4 -12.5 0.0 0 1
4 4 -12.5 0.0 0 5 0.0 0.0 0 1
5 5 0.0 0.0 0 6 15.0 0.0 0 1
6 6 15.0 0.0 0 7 30.0 0.0 0 1
7 7 30.0 0.0 0 8 45.0 0.0 0 1
8 8 45.0 0.0 0 9 60.0 0.0 0 1
9 9 60.0 0.0 0 10 75.0 0.0 0 1
10 10 75.0 0.0 0 11 90.0 0.0 0 1
11 12 0.0 40.0 0 13 0.0 20.0 0 2
12 13 0.0 20.0 0 14 0.0 1.0 0 2
13 1 -50.0 0.0 0 12 0.0 40.0 0 3
14 3 -25.0 0.0 0 13 0.0 20.0 0 3
15 7 30.0 0.0 0 13 0.0 20.0 0 3
16 9 60.0 0.0 0 12 0.0 40.0 0 3
Сечения
№ E F(A) I
1 2D+8 0.5 0.1
2 0.37D+8 0.8 0.07
3 1.7D+8 0.05 1D-7
№1 E
б
= 2*10
8
кН/м
2
,
А
б
= 0,5 м
2
,
I
б
= 0,1 м
4
;
№2 E
пл
= 0,37*10
8
кН/м
2
,
А
пл
= 0,8 м
2
,
I
пл
= 0,07 м
4
;
№3 E
к
= 1,7*10
8
кН/м
2
,
А
в
= 0,05 м
2
,
I
в
= 0,000001 м
4
.
Узлы
№ x y опора шар-
нир
направ-
ление
1 -50.0 0.0 2 0 2
2 -37.5 0.0 0 0 2
3 -25.0 0.0 0 0 2
4 -12.5 0.0 0 0 2
5 0.0 0.0 3 0 2
6 15.0 0.0 0 0 2
7 30.0 0.0 0 0 2
8 45.0 0.0 0 0 2
9 60.0 0.0 0 0 2
10 75.0 0.0 0 0 2
11 90.0 0.0 2 0 2
12 0.0 40.0 0 0 2
13 0.0 20.0 0 0 2
14 0.0 1.0 7 0 2
Распределенные силы
№ вид на-
грузки
стер-
жни
направление значение
(начало)
значение
(конец)
1 1 загруж.1 2 по у -95.6 -95.6
2 1 загруж.2 2 по у -95.6 -95.6
3 1 загруж. 3 2 no у -95.6 -95.6
4 1 загруж.4 2 по у -95.6 -95.6
5 1 загруж.5 2 по у -95.6 -95.6
6 1 загруж.6 2 по у -95.6 -95.6
7 1 загруж.7 2 по у -95.6 -95.6
8 1 загруж.8 2 по у -95.6 -95.6
9 1 загруж.9 2 по у -95.6 -95.6
10 1 загруж. 10 2 по у -95.6 -95.6
Рис. 3.25. Пример подготовки исходных данных для расчета вантового моста
мето
д
ом конечных элементов
76
E
s
= 2*108 кН/м
2
E
к
= 1,5*108 кН/м
2
I
б
= 0.2 м
4
А
б
= 0.5 м
2
А
к
= 0.1 м
2
А
пл
= 0.01 м
2
А
пл
= 0.3 м
2
I
пл
= 0.03 м
4
Узлы
№ x у опо-
ра
шар-
нир
направ
ление
1 0.0 0.0 2 0 2
2 15.0 0.0 0 0 2
3 30.0 0.0 0 0 2
4 50.0 0.0 0 0 2
5 70.0 0.0 0 0 2
6 85.0 0.0 0 0 2
7 100.0 0.0 3 0 2
8 -30.0 0.0 7 0 2
9 0.0 22.0 0 0 2
10 15.0 13.84 0 0 2
11 30.0 8.56 0 0 2
12 50.0 6.0 0 0 2
13 70.0 8.56 0 0 2
14 85.0 13.84 0 0 2
15 100.0 22.0 0 0 2
16 130.0 0.0 7 0 2
17 0.0 1.0 7 0 2
18 100.0 1.0 7 0 2
Стержни
№ на-
чало
x у шар-
нир
ко-
нец
x у шар
нир
сече-
ние
1 1 0.0 0.0 0 2 15.0 0.0 0 1
2 2 15.0 0.0 0 3 30.0 0.0 0 1
3 3 30.0 0.0 0 4 50.0 0.0 0 1
4 4 50.0 0.0 0 5 70.0 0.0 0 1
5 5 70.0 0.0 0 6 85.0 0.0 0 1
6 6 85.0 0.0 0 7 100.0 0.0 0 1
7 8 100.0 0.0 0 9 0.0 22.0 0 2
8 9 0.0 22.0 0 10 15.0 13.84 0 2
9 10 15.0 13.84 0 11 30.0 8,56 0 2
10 11 30.0 8.56 0 12 50.0 6.0 0 2
11 12 50.0 6.0 0 13 70.0 8.56 0 2
12 13 70.0 8.56 0 14 85.0 13.84 0 2
13 14 85.0 13.84 0 15 100.0 22.0 0 2
14 15 100.0 22.0 0 16 130.0 0.0 0 2
15 2 15.0 0.0 0 10 15.0 13.84 0 3
16 3 30.0 0.0 0 11 30.0 8.56 0 3
17 4 50.0 0.0 0 12 50.0 6.0 0 3
18 5 70.0 0.0 0 13 70.0 8.56 0 3
19 6 85.0 0.0 0 14 85.0 13.84 0 3
20 9 0.0 22.0 0 17 0.0 1.0 0 4
21 15 100.0 22.0 0 18 100.0 1.0 0 3
Распределенные силы
№ вид на-
грузки
стержни направ-
ление
значение
(начало)
значение
(конец)
1 1 загруж.1 2 по у -38.0 -38.0
2 1 загруж.2 2 по у -38.0 -38.0
3 1 загруж.3 2 по у -38.0 2
Рис. 3.26. Пример подготовки исходных данных для расчета висячего моста
методом конечных элементов
Сечения
№ E F(A) I
1 2D+8 0.5 0.2
2 1.5D+8 0.1 1D-7
3 1.5D+8 0.01 1D-7
4 0.37D+8 0.3 0.03
77
4. ДИНАМИЧЕСКИЙ И АЭРОДИНАМИЧЕСКИЙ РАСЧЕТЫ
ВИСЯЧИХ И ВАНТОВЫХ МОСТОВ
В обычных конструкциях мостов динамическая и ветровая нагрузки
играют второстепенную роль. Что касается висячих и вантовых мостов
больших пролетов, то их влияние на прочность и надежность сооружения
велико.
Висячие и вантовые мосты испытывают значительные колебания,
вызываемые действием вертикальных и горизонтальных нагрузок, особен-
но периодически изменяющихся во времени. Это обусловлено большой
протяженностью и гибкостью данных сооружений, малым собственным
весом, неблагоприятными динамическими свойствами (низкие частоты и
малые значения логарифмических декрементов колебаний), неблагоприят-
ными аэродинамическими и сейсмическими условиями (районы строи-
тельства, как правило, горные или открытые морские заливы).
Методы динамического и аэродинамического расчета очень сложны
и еще недостаточно разработаны. Это объясняется сложностью происхо-
дящих в пролетных строениях процессов, большим разнообразием конст-
руктивных форм, необходимостью решения громоздких систем нелиней-
ных уравнений, многие коэффициенты которых известны лишь прибли-
женно и не поддаются строгому теоретическому обоснованию.
Поэтому при строительстве крупных мостов проводят исследования
проектируемой конструкции на модели, подвергаемой действию пульси-
рующих вертикальных и горизонтальных нагрузок и воздушного потока в
аэродинамической трубе. Основная цель динамических расчетов и экспе-
риментов состоит в нахождении таких геометрических и жесткостных ха-
рактеристик пролетного строения, при которых исключается возможность
развития опасных колебаний сооружения при эксплуатации.
Исторически в развитии проектирования висячих и вантовых мостов
выделяют три этапа [24]. На первом первостепенным считалось обеспече-
ние статической прочности сооружения. Динамическая и аэродинамиче-
ская устойчивость при этом обеспечивалась совершенно случайно.
Второй этап начался с крушения Такомского моста в 1940 г. Этот пе-
риод характерен повышением внимания к вопросам динамической и аэро-
динамической устойчивости мостов.
Третий этап – это последние 15-20 лет, когда динамика и аэродина-
мика инженерных сооружений сформировались в самостоятельные науч-
ные направления. Подробнее с последними достижениями в этой области
78
можно ознакомиться в [2, 5, 16, 21, 24]. В данном разделе рассматриваются
лишь некоторые основные вопросы динамического и аэродинамического
расчетов в рамках учебного проектирования.
4.1. Основы динамического расчета
4.1.1. Общие сведения из теории колебаний упругих конструкций
[19].
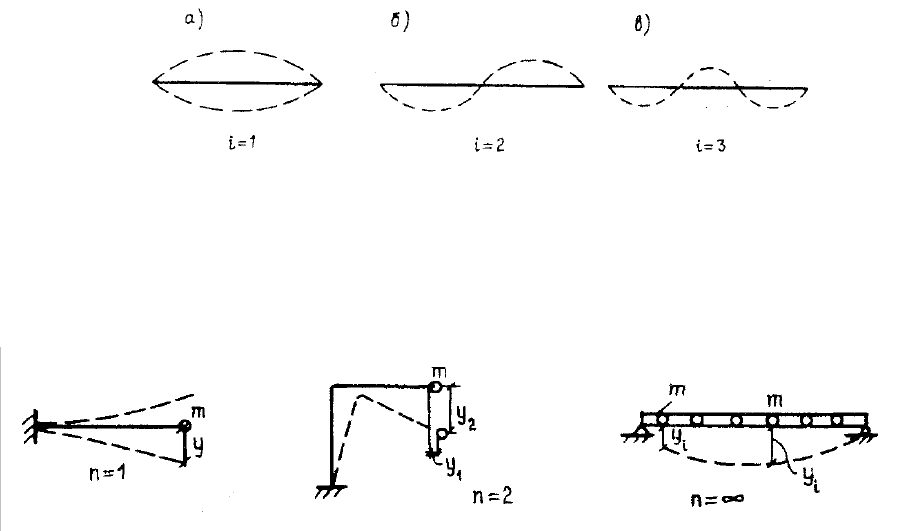
1. Каждое тело (конструкция) может колебаться по многим формам
колебаний, которые характеризуются числом полуволн
i (рис. 4.1). Формы
колебаний при
i ≤ 3 называются основными.
Рис. 4.1. Основные формы колебаний
2. Каждое тело обладает числом степеней свободы n, т. е. числом ко-
ординат, которыми можно описать положение конструкции в любое время
(рис. 4.2). Реальные мосты обладают бесконечным числом степеней свобо-
ды (
n→∞).
Рис. 4.2. Число степеней свободы
3. Каждое тело может испытывать свободные колебания, т. е. колеба-
ния, которые возникают при выведении данного тела из состояния равно-
весия или покоя.
Свободные колебания реальных сооружений с
n степенями свободы
представляют собой набор из происходящих одновременно
собственных
колебаний
, каждое из которых имеет определенную частоту
ω
i
и форму ко-
лебаний (
i = 1, 2, 3, ...).
Круговая частота (
ω
– число колебаний за 2π с, 1/с) и период (Т –
время одного полного колебания, с) связаны между собой (рис. 4.3, а):
79
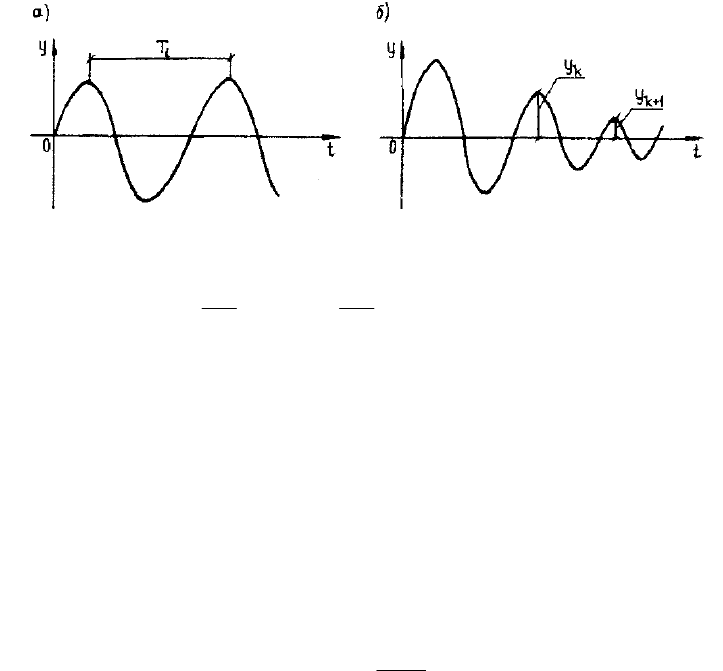
Рис. 4.3. Свободные (а) и затухающие (б) колебания
T =
2
π
ω
и
ω
π
=
2
T
. (4.1)
Для динамического расчета реальных сооружений с
n степенями
свободы наибольшее значение имеют частоты собственных колебаний, ко-
торые, располагаясь в порядке возрастания, образуют
спектр собственных
частот
(
ω
1
, ω
2
, ω
3
,...,ω
n
).
4. За счет внутреннего и внешнего сопротивления практически все
колебания в природе – затухающие (рис. 4.3, 6). Количественная характе-
ристика скорости этого процесса называется
логарифмическим декремен-
том колебаний
:
δ
=
+
ln
v
y
k
k 1
. (4.2)
Для железобетонных мостов
δ
≈ 0,3, для металлических
δ
≈ 0,1, для
висячих и вантовых
δ
≈ 0,015. ..0,07.
5.
Вынужденные колебания возникают под воздействием различных
сил, имеющих свою частоту
θ
. При совпадении частоты возмущающей си-
лы
θ
и частоты свободных колебаний конструкции ω наступает явление ре-
зонанса, т.е. резкое увеличение амплитуды колебаний, а следовательно,
возрастание деформаций и напряжений, что недопустимо при нормальной
эксплуатации сооружения.
4.1.2.
Причины и виды колебаний мостов. Пролетные строения
могут испытывать вертикальные, горизонтальные и крутильные колебания.
Возникновение колебаний в вертикальной плоскости вызывается ди-
намическим воздействием подвижной временной нагрузки, которая явля-
ется по отношению к мосту переменной. Причины этих колебаний:
неровности проезжей части, что при движении транспорта приводит
к толчкам, ударам;
колебания отдельных неуравновешенных частей подвижного состава
(колебания кузова на рессорах, подрессорных частей на пневматических

80
шинах);
ритмическое воздействие гусеничной нагрузки за счет ударов звень-
ев;
ритмическое воздействие от пешеходов, особенно идущих в ногу.
Колебания в горизонтальной плоскости могут возникнуть от воздей-
ствия ветра, если его порывы будут чередоваться с определенным интерва-
лом.
Крутильные колебания пролетного строения возникают от несим-
метричного приложения вертикальных и горизонтальных нагрузок.
4.1.3.
Учет динамического воздействия подвижной нагрузки. Со-
гласно требованиям СНиП 2.05.03-84 учет динамического воздействия
подвижной нагрузки проводится при помощи динамического коэффициен-
та 1+
µ
, величина которого для конструкции висячих и вантовых мостов
равна [1]:
11
50
70
+=+
+
µ
λ
. (4.3)
Кроме того, нормы [1] предусматривают оценку сооружения по пе-
риодам собственных колебаний с целью исключения резонансных явлений.
На основании опытных данных по динамическим характеристикам под-
вижного состава (поездов, автомобилей) и пешеходов техническими нор-
мами устанавливаются резонансные зоны, появления которых следует из-
бегать при проектировании [1, п. 1.48]:
для железнодорожных мостов
Т
l
с
г i,
,
,
≤
001
15
, (4.4)
для автодорожных и пешеходных мостов
Т
в,i
≠ (0,45...0,6) с; (4.5)
Т
г,i
≠ (0,9 ... 1,2) с, (4.6)
где
l - длина пролета; Т
г,i
и Т
в,i
– соответственно периоды горизонтальных и
вертикальных колебаний
i-й формы.
Для висячих мостов необходимо также выполнить проверку на воз-
никновение «параметрического резонанса» [6]. Это явление, связанное с
нелинейными деформациями висячей системы, получило еще название
«перекачки энергии» вследствие того, что происходит процесс перехода
вертикальных колебаний в горизонтальные и наоборот. Параметрический
резонанс наступает при совпадении периода горизонтальных колебаний
