Baggott J. The Quantum Story: A History in 40 Moments

Подождите немного. Документ загружается.

This page intentionally left blank

361

Einstein presented his general theory of relativity in a series of lectures delivered to the

Prussian Academy of Sciences in Berlin, culminating in a ﬁ nal, triumphant lecture on 25

November 1915. Yet within a few short months he was telling the Academy that his new

theory of gravitation might need to be modiﬁ ed:

Due to electron motion inside the atom, the latter should radiate gravitational, as well

as electromagnetic energy, if only a negligible amount. Since nothing like this should

happen in nature, the quantum theory should, it seems, modify not only Maxwell’s

electrodynamics but also the new theory of gravitation.

Attempts to construct a quantum theory of gravity were begun in 1930 by Bohr’s protégé,

Léon Rosenfeld. He noted the problems with divergences that would plague quantum ﬁ eld

theory for many years to come. Soviet physicist Matvei Bronstein later pictured the chal-

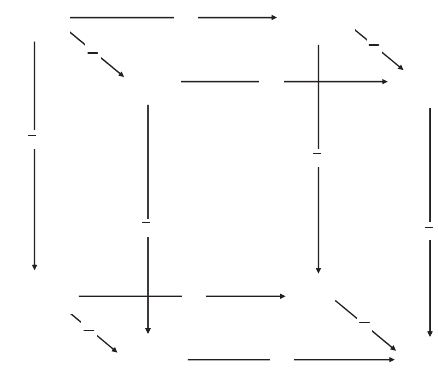
lenge in the form of a cube whose faces are distinguished by three fundamental physical

constants. These are the speed of light, c, Planck’s constant divided by 2p, ħ and Newton’s

gravitational constant, G.

Proceeding from the top-left-back corner to Newton’s theory

of gravitation at the top-right-back corner requires the introduction of G. Introducing a

The Wavefunction of the

Universe

Princeton, July 1966

This is now known as the Bronstein cube. Strictly speaking, as pulling the physical theories

back to the top-left corner (which we can denote as ‘Galilean physics’) requires the assumption

ħ = 0, G = 0, and c = ∞, it might be better to think of the constants in terms of the group ħ, G,

and 1/c.

the quantum story

362

ﬁ nite speed of light c takes us to general relativity at the top-right-front corner. To get to a

quantum version of general relativity at the bottom-right-front corner requires the further

introduction of ħ.

Just looking at this cube suggests at least two directions to a quantum version of gen-

eral relativity. One can seek to ‘quantize’ general relativity, a step that Einstein himself

tended to dismiss as ‘childish’. A second direction involves starting with relativistic quan-

tum ﬁ eld theory and making it conform to the general covariance requirements of general

relativity.

There is, of course, a third direction (not pictured), which is to start afresh.

Whichever direction we take, we run into a series of profound problems right at the

outset. General relativity is about the motions of large-scale bodies such as planets, stars,

solar systems, galaxies, and the entire universe within a four-dimensional space–time.

In general relativity these motions are described by a set of complex mathematical equa-

tions known as Einstein’s gravitational ﬁ eld equations. They are complex because the

General covariance means that the physical laws described by the theory are invariant to

arbitrary coordinate transformations.

Which acknowledges that if you want to get there, then you shouldn’t start from here.

Galilean

physics

Newtonian

physics

special

relativity

general

relativity

quantum

classical

non-relativistic

relativistic

quantum

mechanics

quantum

field theory

quantum

gravity

???

quantum

non-gravitational

gravitational

fig 26 A modern interpretation of the Bronstein cube. Each face of the cube rep-

resents a domain of theoretical physics, and passing from one domain to another

involves introducing the physical constants c,

–

h and G. The ??? represents a quantized

but non-relativistic version of Newtonian physics. Adapted from Roger Penrose, The

Large, the Small and the Human Mind. Cambridge University Press, 1997, p. 91.

the wavefunction of the universe

363

mass they consider distorts the geometry of space–time around it and the geometry of the

space–time around it governs how the mass moves.

But space–time itself is contained entirely within general relativity—it is a fundamental

dynamical variable of the theory. The theory itself constructs the framework within which

mass moves and events happen. In this sense the theory is ‘background independent’—it

does not presuppose the existence of a background framework against which motions of

large masses are to be registered. Quantum theory, in contrast, presumes precisely this. It

is ‘background dependent’, requiring a classical ‘container’ of space and time within which

the wavefunctions of quantum particles evolve.

Then we run into the uncertainty principle, which changes our understanding of the very

meaning of ‘empty’ space. It is not empty at all. It is ﬁ lled with virtual particles, ﬂ ickering in

and out of existence.

General relativity assumes that space–time is certain, and not subject

to quantum theory’s characteristically probabilistic laws. In general relativity we can be cer-

tain that space–time is ‘here’ or ‘there’, curves this way or that way, at this rate or that rate.

Early attempts to forge a quantum theory of gravity were premature and frustrated.

Momentum began to pick up again in the early 1950s.

In May 1952, John Wheeler at Princeton pulled a new bound notebook

from his shelf and labelled it ‘Relativity I’. He was pleased to learn that he

had been given the go-ahead to teach a course on relativity, and thought

to get into the subject properly by writing a book about it. ‘That fall,

ﬁ fteen graduate students enrolled in my course,’ Wheeler explained. ‘It

was the ﬁ rst time that a relativity course had been offered at Princeton—

and together we worked our way through the subject, trying to get behind

the mathematical formalism that had dominated the theory for decades,

looking for real, tangible physics.’

In fact, when Einstein ﬁ rst developed his ﬁ eld equations in 1915 he con-

sidered them too complex to solve. Yet only a year later German physi-

cist Karl Schwarzchild had produced a solution, which he discovered

whilst serving in the German army on the Russian front. Schwarzchild’s

solutions predicted that a particularly massive body could collapse under

The effect of the creation and destruction of these virtual particles in empty space can be

demonstrated in the laboratory through something called the Casimir effect, discovered in 1948

by Dutch physicist Hendrik Casimir. Two closely spaced metal plates will actually be pushed

closer together due to the fact that the pressure from virtual photons in the gap between the

plates no longer balances the pressure of virtual photons outside the gap.

the quantum story

364

the inﬂ uence of its own gravity to a so-called singularity. Such a singularity

would distort the space–time around it so much that nothing, not even

light, would escape its ‘event horizon’. Wheeler was initially troubled by

this idea, but grew to accept it. He called it a black hole.

The early predictions of general relativity are well known. The theory

helped to account for a wobble in the orbit of the planet Mercury around

the sun, a wobble that Newton’s gravity couldn’t explain. Einstein also

predicted that light from a distant star passing by the sun would be bent

in its path by the curvature of space–time. Such bending of starlight was

proven by observations made during a solar eclipse in 1919, and helped

to make Einstein a cultural icon of the twentieth century.

A few years after teaching his ﬁ rst courses on general relativity, Wheeler

began to think about the potential implications of quantum effects. In

seeking to base the search for a theory of quantum gravity on the funda-

mental concepts of geometry, he elucidated a theory of quantum geomet-

rodynamics, an allusion to the parallels with quantum electrodynamics, or

QED. In discussions with one of his students, American Charles Misner,

he applied the logic of quantum uncertainty to space–time itself, replacing

the perspective of a ﬂ at or gently curving space–time with the chaos of

uncertainty and quantum ﬂ uctuations.

The uncertainty principle is a licence for the bizarre, and in the quan-

tum domain the topology of space–time becomes twisted and tortured

and riddled with bumps, lumps, and tunnels—‘wormholes’ connecting

one part of space–time with another. Wheeler referred to this as quantum

or space–time ‘foam’.

In the absence of a fully ﬂ edged theory of quantum gravity these

were simply ideas about what space–time might look like at extremely

small distances, of the order of a millionth of a billionth of a billionth

of a billionth of a centimetre (a distance called the Planck length) and in

extremely small time intervals of the order of a tenth of a millionth of a

trillionth of a trillionth of a trillionth of a second (called the Planck time).

The Planck length and Planck time can be calculated from the fundamental constants G, ħ,

and c. The Planck length is given by

Gc

and the Planck time is given by

Gc

(the Planck

length divided by c).

the wavefunction of the universe

365

In fact, on these scales the very concept of distance and time interval lose

their meaning. There is no distance smaller than the Planck length, no

time shorter than the Planck time.

Misner worked on aspects of classical general relativity under Wheel-

er’s direction, publishing a long paper in the journal Annals of Physics in

1957 and intending to submit this paper as his Princeton PhD thesis. He

then discovered that the key ideas in his work had been published already

in 1925. Undaunted, he turned his attention to quantum gravity. He pub-

lished details of an approach to the Feynman quantization of general

relativity in the journal Reviews of Modern Physics later that same year.

It was in this paper that Misner suggested three lines of research on

quantum gravity, much like three possible routes to the conquest of

Everest. The quantization of general relativity could be approached

by ﬁ rst recasting the theory into a form more familiar in quantum

mechanics (this is a so-called constrained Hamiltonian formulation).

This reformulation is a kind of stepping-stone. The second step is to

apply a quantization technique. In the 1940s and early 1950s German

theorist Peter Bergman at the Institute for Advanced Study and Dirac

in Cambridge had worked on quantization techniques based on gauge

symmetries. This became known as canonical quantization, and the

line of research became known as the canonical approach to quantum

gravity.

An alternative quantization technique was to apply Feynman’s path

integral or sum over histories approach, a technique that Misner had out-

lined in his paper. The third route was to devise a quantum ﬁ eld theory of

the gravitational ﬁ eld which conforms to the general covariance require-

ments of general relativity using a ﬁ ctitious ‘ﬂ at space’. Once constructed,

it was assumed that the resulting ﬁ eld equations could be solved using

perturbation techniques, in much the same way that the equations of

QED had been solved, perhaps using Feynman diagrams. This is known

as the covariant approach.

Although purportedly pursuing the same objective, the canonical and

covariant approaches looked distinctly different. Not surprisingly, as it builds

It involves structuring the equations to deﬁ ne classical variables (position, momentum)

which are then replaced by their quantum-mechanical operator equivalents.

the quantum story

366

on general relativity, the canonical approach emphasizes the geometry of

space–time and the (quantum) dynamics of objects moving within this

geometry. The covariant approach emphasizes the quantum ﬁ eld and the

graviton as force carrier. Although some theorists acknowledged the bene-

ﬁ ts of pursuing multiple lines of research, the great conceptual divisions and

lack of common ground between these approaches was already ominous.

Work on the canonical approach had led to some puzzling results. Gen-

eral relativity demands that space and time be treated on an equal footing

and there is no absolute space–time coordinate system—all coordinate

systems are arbitrary. In general relativity there is no meaningful ‘here’ and

‘there’ or ‘now’ and ‘then’. The theory rather deals with space–time intervals.

Differences in time enter the theory as ct, the time interval multiplied

by the speed of light, which has the same units as a distance interval. Once

entered, the time dimension becomes in principle indistinguishable from

the three spatial dimensions in a four-dimensional space–time.

However, what Dirac discovered is that in his constrained Hamiltonian

reformulation of general relativity the dynamics are governed by only three

of the four dimensions. ‘This result,’ he declared, ‘has led me to doubt how

fundamental the four-dimensional requirement in physics is.’ The three

dimensions, called a three-space, hold all the information about the geo-

metrical relationships between masses and, to all intents and purposes,

look like three spatial dimensions. Space–time had been unpicked, and

although time had not exactly disappeared in this reformulation, it had

become rather mysterious and elusive.

In fact, time had become the result

of the changing geometrical relationships between material objects.

In 1961, Misner, together with Americans Richard Arnowitt and Stanley

Deser, published a greatly simpliﬁ ed elaboration of the constrained

In fact, space–time intervals are given by

-dct

(),

where d is the difference in spatial

coordinates (simpliﬁ ed here to one dimension), t is the time difference, and c is the speed of

light. This means that some intervals can be imaginary (i.e. they are multiplied by i, the square-

root of −1), and this is a characteristic ‘signature’ of a time interval. For example, the space–time

interval between your current position and this same position in ﬁ ve minutes’ time is roughly

90i million kilometres.

Of course, the nature of time has been the subject of intense debate among philosophers

for centuries. Deep questions concerning the implications of both special and general relativity

for our understanding of time had rumbled virtually from the moment the theories had been

written down.

the wavefunction of the universe

367

Hamiltonian formulation of general relativity, building on the earlier

work of Dirac and Bergman. In the Arnowitt, Deser, and Misner (ADM)

formulation, space–time is treated as a series of purely spatial ‘hypersur-

faces’, which may individually be curved, connected together through

their relationships one with another representing the evolution of the

system in time.

The stage was set for a signiﬁ cant development in the search for a

quantum theory of gravity.

Many of the possible solutions of Einstein’s gravitational ﬁ eld equations

describe a universe in which space–time itself is expanding. Einstein ini-

tially resisted the idea of an expanding universe and fudged his equations

to produce static solutions, by introducing an arbitrary ‘cosmological

constant’. But the fact that our own universe is indeed expanding was

suggested by American astronomer Edwin Hubble’s observations in

1929. He noted that distant galaxies are all receding from us at rates that

increase with their distance, much like dots scribbled on a deﬂ ated bal-

loon will all move apart from each other as the balloon is inﬂ ated.

If the universe is expanding then this implies that it had an origin at

some point in time in an inﬁ nitesimally small, immensely hot ‘big bang’.

Subsequent expansion and cooling would then give rise to the universe

as we know it today.

The violent explosion of radiation some time after a hot big bang was pre-

dicted to have left a detectable signature. This radiation would pervade all of

space, cooled to a few degrees or tens of degrees above absolute zero as the

universe expanded. It would take the form of microwave radiation. Whilst

working on radar at MIT in 1946, physicist Robert Dicke had set a limit on

this background radiation at less than 20 degrees above absolute zero.

A few years later George Gamow, Ralph Alpher, and Robert Herman

had predicted a temperature of ﬁ ve degrees above absolute zero. In 1965,

Dicke, together with Princeton physicists Jim Peebles, David Wilkinson,

and Peter Roll, were building an apparatus to try to detect this micro-

wave background radiation when they discovered that it had already

been found. Arno Penzias and Robert Wilson at nearby Bell Laboratories

Absolute zero (0 kelvin) is equal to −273.15 °C.

the quantum story

368

in Holmdel, New Jersey, had the previous year detected a persistent and

annoying hiss of microwave radiation using a highly sensitive 20-foot

horn antenna. It was coming uniformly from all directions in the sky. Try

as they might, they could not eliminate what they took to be interference.

They did not know what it was.

Penzias was subsequently advised of a preprint by Peebles concern-

ing the microwave background radiation, and he and Wilson made the

connection. The radiation they had discovered ﬁ t closely with the Princ-

eton physicists’ predictions, indicating a radiation temperature of about

three degrees above absolute zero. Penzias and Wilson and the Princ-

eton group published companion papers announcing the discovery in

the Astrophysical Journal Letters in May 1965.

The big bang was a proven hypothesis. This meant that our universe

had an origin about 12 or 13 billion years ago.

And now there could

be no denying it. Although the universe is the ultimate macroscopic

object, the ﬁ rst moments in the creation of all things—space, time, force,

radiation, matter—were indisputably microscopic in scale. The origin of

the universe was a quantum phenomenon, governed (for better or worse)

by quantum laws. What was needed to understand these early moments

was a quantum cosmology, of which a quantum theory of gravity would be

a fundamental component.

American theorist Bryce DeWitt had studied under Schwinger at

Harvard University, completing his doctorate in 1950. He had preferred

to study at Harvard rather than Caltech because of his passion for row-

ing. He met and married Cecille Morette whilst working at the Institute

for Advanced Study. After conducting research at a number of insti-

tutes overseas, accompanied by his wife, he returned to America in 1952

and worked ﬁ rst at the Lawrence Livermore National Laboratory before

moving to the University of North Carolina at Chapel Hill in 1956.

When in 1965 Wheeler realized he had to make a short stopover

at Raleigh-Durham airport in North Carolina, he called DeWitt and

asked to meet him there. DeWitt arrived as Wheeler was waiting for

More recent satellite observations of the microwave background radiation have allowed

the origin of the universe to be set about 13.7 billion years ago, give or take a couple of hundred

million years.

the wavefunction of the universe

369

his connecting ﬂ ight. They discussed recent work on the reformulation

of general relativity and DeWitt mumbled something about doing for

relativity what Schrödinger had done for the hydrogen atom in 1925. To

DeWitt’s surprise, Wheeler was immediately enthusiastic, declaring that

the equation for quantum gravity had been found.

DeWitt subsequently spent a short time at the Institute for Advanced

Study in Princeton, where he held further conversations with Wheeler

and developed the ﬁ rst formal theory of quantum gravity. He pro-

duced a series of papers, submitted to Physical Review in July 1966 and

eventually published in August 1967.

The ﬁ rst of these describe a

canonical approach applied to a simple model universe based on the

solutions of Einstein’s gravitational ﬁ eld equations ﬁ rst derived in

1922 by Russian mathematician Alexander Friedmann. In a Friedmann

universe, space–time is homogeneous and expanding uniformly in

all directions. DeWitt ﬁ lled this model universe with non-interacting

material particles at rest.

As Dirac had observed, so DeWitt now noted that in his quantum wave

equation of the universe, time had disappeared. The wavefunction, which

DeWitt called ‘the wavefunction of the universe’, was found to depend

only on the geometry of the resulting three-space. It was the wavefunc-

tion of a stationary universe with zero total energy. He wrote: ‘. . . one

therefore comes to the conclusion that nothing ever happens in quantum

gravidynamics, that the quantum theory can never yield anything but a

static picture of the world.’ His solution was to combine many different

wavefunctions into a ‘wavepacket’ state, which would trace out a classical

trajectory on the three-space.

DeWitt’s result implies that time is ‘phenomenological’. It suggests

that our experience of time is not born of an intrinsic, fundamental ele-

ment of reality called ‘time’. What we experience is rather the changing

geometry of the universe and the masses within it, which we synthesize

in our minds and interpret as evolving instants of time.

DeWitt had no clear sense of how the wavefunction of the universe

should be interpreted and, in mitigation, cited historical precedent.

It seems that the delay was, in part, the result of difﬁ culties concerning page charges.