Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics
Подождите немного. Документ загружается.


12-3 Ranging by local positioning systems (LPS) 201
where X
0
, Y
0
are the coordinates of the unknown station, and X
i
, Y
i
the coordi-
nates of the known station and S
i
the measured distance.
The objective function in case of n measured distance is defined as the sum of
the square residuals
∆ =
n
X
i=1
e
2
i
=
n
X
i=1
h
(X
i
− X
0
)
2
+ (Y
i
− Y
0
)
2
− S
2
i
i
2
.
The determined square system can easily be created symbolically with Com-
puter Algebra Systems, according to the necessary condition of the minimum,
f
1
=
∂∆
∂X
0
=J
0
+ J
1
X
0
+ J
2
X
2
0
+ J
3
X
3
0
+ J
4
Y
0
+ J
5
X
0
Y
0
+ J
6
Y
2
0
+ J
7
X
0
Y
2
0
= 0
f
2
=
∂∆
∂Y
0
=K
0
+ K
1
X
0
+ K
2
X
2
0
+ K
3
Y
0
+ K
4
X
0
Y
0
+ K
5
X
2
0
Y
0
+ K
6
Y
2
0
+ K
7
Y
3
0
= 0
where
J
0
→ 4
n
X
i=1
S
2
i
X
i
− X
3
i
− X
i
Y
2
i
, J
1
→ 4
n
X
i=1
−S
2
i
+ 3X
2
i
+ Y
2
i
,
J
2
→ −12
n
X
i=1
X
i
, J
3
→ 4n, J
4
→ 8
n
X
i=1
X
i
Y
i
, J
5
→ −8
n
X
i=1
Y
i
,
J
6
→ −4
n
X
i=1
X
i
, J
7
→ 4n
K
0
→ 4
n
X
i=1
S
2
i
Y
i
− X
2
i
Y
i
− Y
3
i
, K
1
→ 8
n
X
i=1
X
i
Y
i
,
K
2
→ −4
n
X
i=1
Y
i
, K
3
→ 4
n
X
i=1
−S
2
i
+ X
2
i
+ 3Y
2
i
, K
4
→ −8
n
X
i=1
X
i
,
K
5
→ 4n, K
6
→ −12
n
X
i=1
Y
i
, K
7
→ 4n
Now we should solve this third order polynomial square system. The complex-
ity of the system is not dependent on the number of redundant data. Only the
coefficients change if we have more measured distances. Let use the same data in
Table 12.11, but in order to increase the precision of the computation the values
of the coordinates and the distances are rationalized,
X
1
→
2408881
50
, Y
1
→
163282
25
, S
1
→
611023
1000
,
X
2
→
992003
20
, Y
2
→
718519
100
, S
2
→
764741
500
,
X
3
→
4983093
100
, Y
3
→
567069
100
, S
3
→
330971
250
,
X
4
→
4786391
100
, Y
4
→
126931
25
, S
4
→
301631
250
Now our system to solve is the following:

202 12 Positioning by ranging
f
1
= −
237200
12500000
+
576246
50000
X
0
−
586418
25
X
2
0
+ 16X
3
0
+
598320
625
Y
0
−
978576
5
X
0
Y
0
−
195473
25
Y
2
0
+ 16X
0
Y
2
0
f
2
= −
148689
6250000
+
598321
625
X
0
−
489288
5
X
2
0
+
200121
50000
Y
0
−
390945
25
X
0
Y
0
+ 16X
2
0
Y
0
−
1467864
5
Y
2
0
+ 16Y
3
0
This system can be solved with Groebner basis using Mathematica:
GroebnerBasis[{f
1
, f
2
}, {X
0
, Y
0
}];
which leads to a univariate and a two-variate polynomials
g
1
= L
0
+ L
1
Y
0
+ L
2
Y
2
0
+ L
3
Y
3
0
+ L
4
Y
4
0
+ L
5
Y
5
0
g
2
= M
0
+ M
1
X
0
+ M
2
Y
0
+ M
3
Y
2
0
+ M
4
Y
3
0
+ M
5
Y
4
0
where
L
0
→ − 3.93690 ×10
55
,
L
1
→3.25850 × 10
52
,
L
2
→ − 1.08236 ×10
49
,
L
3
→1.80350 × 10
45
,
L
4
→ − 1.50752 ×10
41
,
L
5
→5.05731 × 10
36
M
0
→4.22105 × 10
85
,
M
1
→1.31676 × 10
79
,
M
2
→ − 2.96087 ×10
82
,
M
3
→7.67600 × 10
78
,
M
4
→ − 8.85305 ×10
74
,
M
5
→3.83418 × 10
70
Let us compute the roots of g
1
univariate polynomial (Y
0
),
Y
0
→ 6058.9782,
Y
0
→ 5747.6051 − 710.6398ı,
Y
0
→ 5747.6051 + 710.6398ı,
Y
0
→ 6127.2461 − 873.7323ı,
Y
0
→ 6127.2461 + 873.7323ı
There is only one real solution, the first. Knowing Y
0
, X
0
can be calculated
from the second equation (g
2
) which is linear in X
0
. Then the solution is,
12-3 Ranging by local positioning systems (LPS) 203
X
0
= 48565.2699 Y
0
= 6058.9782.
The result of ALESS is almost the same as Gauss-Jacobi’s BLUUE and tra-
ditional least squares solution (see Table 12.13) (the difference between them is
about 3 m m).
12-32 Three-dimensional ranging
12-321 Closed form three-dimensional ranging
Three-dimensional ranging problem differs from the planar ranging in terms of
the number of unknowns to be determined. In the planar case, the interest is
to obtain from the measured distances the two-dimensional coordinates {x
0
, y
0
}
of the unknown station P . For the three-dimensional ranging, the coordinates
{X, Y, Z} have to be derived from the measured distances. Since three coordi-
nates are involved, distances must be measured to at least three known stations
for the solution to be determined. If the stations observed are more than three,
the case is an overdetermined one. The main task involved is the determination
of the unknown position of a station given distance me asurements from unknown
station P ∈ E
3
, to three known stations P
i
∈ E
3
| i = 1, 2, 3. In general, the three-
dimensional closed form ranging problem can be formulated as follows: Given
distance measurements from an unknown station P ∈ E
3
to a minimum of three
known stations P
i
∈ E
3
| i = 1, 2, 3, determine the position {X, Y, Z} of the un-
known station P ∈ E
3
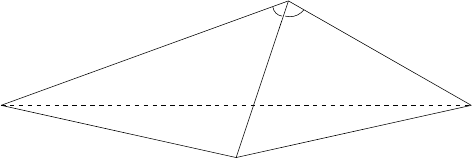
(see e.g., Fig. 13.4). From the three nonlinear Pythagoras
P
2
P
3
S
3
P
S
2
S
31
ψ
12
ψ
23
P
1
S
1
S
12
S
23
Figure 12.13. Tetrahedron: three-dimensional distance and space angle observations
distance observation equations (12.53) in Solution 12.5, two equations with three
unknowns are derived. Equation (12.53) is expanded in the form given by (12.54)
and differenced to give (12.55) with the quadratic terms
X
2
, Y
2
, Z
2
eliminated.
Collecting all the known terms of (12.55) to the right-hand-side and those relating
to the unknowns (i.e., a and b) on the left-hand-side leads to (12.57). T he solution
of the unknown terms {X, Y, Z} now involves solving (12.56), which has two equa-
tions with three unknowns. Equation (12.56) is similar to (12.4) on p. 177 which
was considered in the case of GPS pseudo-range. Four approaches are considered
204 12 Positioning by ranging
for solving (12.56), w here more unknowns than equations are solved. Similar to
the case of GPS pseudo-ranging that we considered, the underdetermined system
(12.56) is overcome by determining two of the unknowns in terms of the third
unknown (e.g., X = g(Z), Y = g(Z)).
Solution 12.5 (Differencing of the nonlinear distance equations).
S
2
1
= (X
1
− X)
2
+ (Y
1
− Y )
2
+ (Z
1
− Z)
2
S
2
2
= (X
2
− X)
2
+ (Y
2
− Y )
2
+ (Z
2
− Z)
2
S
2
3
= (X
3
− X)
2
+ (Y
3
− Y )
2
+ (Z
3
− Z)
2
(12.53)
S
2
1
= X
2
1
+ Y
2
1
+ Z
2
1
+ X
2
+ Y
2
+ Z
2
− 2X
1
X − 2Y
1
Y − 2Z
1
Z
S
2
2
= X
2
2
+ Y
2
2
+ Z
2
2
+ X
2
+ Y
2
+ Z
2
− 2X
2
X − 2Y
2
Y − 2Z
2
Z
S
2
3
= X
2
3
+ Y
2
3
+ Z
2
3
+ X
2
+ Y
2
+ Z
2
− 2X
3
X − 2Y
3
Y − 2Z
3
Z
(12.54)
differencing above
S
2
1
− S
2
2
= X
2
1
− X
2
2
+ Y
2
1
− Y
2
2
+ Z
2
1
− Z
2
2
+ a
S
2
2
− S
2
3
= X
2
2
− X
2
3
+ Y
2
2
− Y
2
3
+ Z
2
2
− Z
2
3
+ b,
(12.55)
where
a = 2X(X
2
− X
1
) + 2Y (Y
2
− Y
1
) + 2Z(Z
2
− Z
1
)
b = 2X(X
3
− X
2
) + 2Y (Y
3
− Y
2
) + 2Z(Z
3
− Z
2
).
(12.56)
Making a and b the subject of the formula in (12.55) leads to
a = S
2
1
− S
2
2
− X
2
1
+ X
2
2
− Y
2
1
+ Y
2
2
− Z
2
1
+ Z
2
2
b = S
2
2
− S
2
3
− X
2
2
+ X
2
3
− Y
2
2
+ Y
2
3
− Z
2
2
+ Z
2
3
.
(12.57)
12-322 Conventional approaches
Solution by elimination approach-1
In the elimination approach presented in Solution 12.6, (12.56) is expressed in the
form (12.58); w ith two equations and two unknowns {X, Y }. In this equation, Z
is treated as a constant. By first eliminating Y, X is obtained in terms of Z and
substituted in either of the two expressions of (12.58) to give the value of Y . The
values of {X, Y } are depicted in (12.59) with the coefficients {c, d, e, f} given by
(12.60). The values of {X, Y } in (12.59) are substituted in the first expression of
(12.53) to give the quadratic equation (12.61) in terms of Z as the unknown. The
quadratic formula (3.8) on p. 24 is then applied to obtain the two solutions of Z
(see the second e xpression of (12.61)). The coefficients {g, h, i} are given in (12.62).
Once we solve (12.61) for Z, we substitute in (12.59) to obtain the c orresponding
pair of solutions for {X, Y }.
Solution 12.6 (Solution by elimination).
2X(X
2
− X
1
) + 2Y (Y
2
− Y
1
) = a −2Z(Z
2
− Z
1
)
2X(X
3
− X
2
) + 2Y (Y
3
− Y
2
) = b −2Z(Z
3
− Z
2
)
(12.58)

12-3 Ranging by local positioning systems (LPS) 205
X = c − dZ
Y = e − f Z
(12.59)
c =
a(Y
3
− Y
2
) −b(Y
2
− Y
1
)
2 {(X
2
− X
1
)(Y
3
− Y
2
) −(X
3
− X
2
)(Y
2
− Y
1
)}
d =
{(Z
2
− Z
1
)(Y
3
− Y
2
) −(Z
3
− Z
2
)(Y
2
− Y
1
)}Z
{(X
2
− X
1
)(Y
3
− Y
2
) −(X
3
− X
2
)(Y
2
− Y
1
)}
e =
a(X
3
− X
2
) −b(X
2
− X
1
)
2 {(Y
2
− Y
1
)(X
3
− X
2
) −(Y
3
− Y
2
)(X
2
− X
1
)}
f =
{(Z
2
− Z
1
)(X
3
− X
2
) −(Z
3
− Z
2
)(X
2
− X
1
)}Z
{(Y
2
− Y
1
)(X
3
− X
2
) −(Y
3
− Y
2
)(X
2
− X
1
)}
(12.60)
substituting 12.59 in 12.53i
gZ
2
+ hZ + i = 0
Z
1,2
=
−h ±
p
h
2
− 4gi
2g
,
(12.61)
where
g = d
2
+ f
2
+ 1
h = 2(dX
1
+ fY
1
− Z
1
− cd − ef)
i = X
2
1
+ Y
2
1
+ Z
2
1
− 2X
1
c −2Y
1
e −S
2
1
+ c
2
+ e
2
.
(12.62)
12-323 Solution by elimination approach-2
The second approach presented in Solution 12.7 involves first expressing (12.56) in
the form (12.63) which can also be expressed in matrix form as in (12.64). We now
seek the matrix solution of {Y, Z} in terms of the unknown element X as expressed
by (12.65), which is written in a simpler form in (12.66). The elements of (12.66)
are as given by (12.67). The solution of (12.65) for {Y, Z} in terms of X is given
by (12.68), (12.69) and (12.70). The coefficients of (12.70) are given by (12.71).
Substituting the obtained values of {Y, Z} in terms of X in the first expression of
(12.53) leads to quadratic equation (12.72) in terms of X as an unknown. Applying
the quadratic formula (3.8) on p. 24, two solutions for X are obtained as in the
second expression of (12.72). These are then substituted back in (12.70) to obtain
the values of {Y, Z}. The coefficients {l, m, n} in (12.72) are given by (12.73).
A pair of solutions {X
1
, Y
1
, Z
1
} and {X
2
, Y
2
, Z
2
} are obtained. For GPS pseudo-
ranging in Sect. 12-2, we saw that the admissible solution could easily be chosen
from the pair of solutions. The desired solution was easily chosen as one set of solu-
tion was in space while the other set was on the Earth’s surface. The solution could
therefore be distinguished by com puting the radial distances (positional norms).
The admissible solution from the pair of the three-dimensional LPS ranging tech-
niques is however difficult to isolate and must be obtained with the help of prior
information, e.g., from an existing map.
206 12 Positioning by ranging
Solution 12.7 (Solution by matrix approach).
2Y (Y
2
− Y
1
) + 2Z(Z
2
− Z
1
) = a −2X(X
2
− X
1
)
2Y (Y
3
− Y
2
) + 2Z(Z
3
− Z
2
) = b −2X(X
3
− X
2
)
(12.63)
Y
2
− Y
1
Z
2
− Z
1
Y
3
− Y
2
Z
3
− Z
2
Y
Z
=
1
2
a
b
− 2
X
2
− X
1
X
3
− X
2
X
(12.64)
Y
Z
=
1
2
d
Z
3
− Z
2
−(Z
2
− Z
1
)
−(Y
3
− Y
2
) (Y
2
− Y
1
)
a
b
− 2
X
2
− X
1
X
3
− X
2
X,
(12.65)
with
d = {(Y
2
− Y
1
)(Z
3
− Z
2
) −(Y
3
− Y
2
)(Z
2
− Z
1
)}
−1
.
Y
Z
= {a
11
a
22
− a
12
a
21
}
−1
a
22
−a
12
−a
21
a
11
b
1
b
2
+
c
1
c
2
X,
(12.66)
where
a
11
= Y
2
− Y
1
, a
12
= Z
2
− Z
1
, a
21
= Y
3
− Y
2
, a
22
= Z
3
− Z
2
c
1
= −(X
2
− X
1
), c
2
= −(X
3
− X
2
) , b
1
=
1
2
a, b
2
=
1
2
b.
(12.67)
Y = {a
11
a
22
− a
12
a
21
}
−1
{a
22
(b
1
+ c
1
X) −a
12
(b
2
+ c
2
X)}
Z = {a
11
a
22
− a
12
a
21
}
−1
{a
11
(b
2
+ c
2
X) −a
21
(b
1
+ c
1
X)}
(12.68)
Y = e [{a
22
b
1
− a
12
b
2
} + {a
22
c
1
− a
12
c
2
}X]
Z = e [{a
11
b
2
− a
21
b
1
} + {a
11
c
2
− a
21
c
1
}X]
(12.69)
Y = e(f + gX)
Z = e(h + iX)
(12.70)
e = (a
11
a
22
− a
12
a
21
)
−1
, f = a
22
b
1
− a
12
b
2
, g = a
22
c
1
− a
12
c
2
h = a
11
b
2
− a
21
b
1
, i = a
11
c
2
− a
21
c
1
, k = X
2
1
+ Y
2
1
+ Z
2
1
.
(12.71)
substituting (12.70) in (12.53i)
lX
2
+ mX + n = 0
X
1,2
=
−m ±
√
m
2
− 4ln
2l
,
(12.72)
where
l = e
2
i
2
+ e
2
g
2
+ 1
m = 2(e
2
fg + e
2
hi −X
1
− egY
1
− eiZ
1
)
n = k − S
2
1
− 2Y
1
ef + e
2
f
2
− 2Z
1
eh + e
2
h
2
.
(12.73)
12-324 Groebner basis approach
Equation (12.56) is expressed in algebraic form (12.74) in Solution 12.8 with the
coefficients as in (12.75). Groebner basis of (12.74) is then obtained in (12.76)
using (4.36) on p. 45. The obtain Groebner basis solution of the three-dimensional
ranging problem is presented in (12.77). The first expression of (12.77) is solved
for Y = g
1
(Z), and the output presented in (12.78). This value is substituted in
the second expression of (12.77) to give X = g
2
(Z) in (12.79). The obtained values

12-3 Ranging by local positioning systems (LPS) 207
of Y and X are substituted in the first expression of (12.53) to give a quadratic
equation in Z. Once this quadratic equation has been solved for Z using (3.8) on p.
24, the values Y and X are obtained from (12.78) and (12.79) respectively. Instead
of solving for Y = g
1
(Z) and substituting in the second expression of (12.77) to
give X = g
2
(Z), direct solution of X = g(Z) in (12.80) could be obtained by
computing the reduced Groebner basis (4.38) on p. 45. Similarly we could obtain
Y = g(Z) alone by replacing Y with X in the option part of the reduced Groebner
basis.
Solution 12.8 (Groebner basis solution).
a
02
X + b
02
Y + c
02
Z + f
02
= 0
a
12
X + b
12
Y + c
12
Z + f
12
= 0
(12.74)
a
02
= 2(X
1
− X
2
), b
02
= 2(Y
1
− Y
2
), c
02
= 2(Z
1
− Z
2
)
a
12
= 2(X
2
− X
3
), b
12
= 2(Y
2
− Y
3
), c
12
= 2(Z
2
− Z
3
)
f
02
= (S
2
1
− X
2
1
− Y
2
1
− Z
2
1
) −(S
2
2
− X
2
2
− Y
2
2
− Z
2
2
)
f
12
= (S
2
2
− X
2
2
− Y
2
2
− Z
2
2
) −(S
2
3
− X
2
3
− Y
2
3
− Z
2
3
).
(12.75)
GroebnerBasis[{a
02
X + b
02
Y + c
02
Z + f
02
, a
12
X + b
12
Y + c
12
Z + f
12
}, {X, Y }] (12.76)
g
1
= a
02
b
12
Y − a
12
b
02
Y − a
12
c
02
Z + a
02
c
12
Z + a
02
f
12
− a
12
f
02
g
2
= a
12
X + b
12
Y + c
12
Z + f
12
g
3
= a
02
X + b
02
Y + c
02
Z + f
02
.
(12.77)
Y =
{(a
12
c
02
− a
02
c
12
)Z + a
12
f
02
− a
02
f
12
}
(a
02
b
12
− a
12
b
02
)
(12.78)
X =
−(b
12
Y + c
12
Z + f
12
)
a
12
, (12.79)
or
X =
{(b
02
c
12
− b
12
c
02
)Z + b
02
f
12
− b
12
f
02
}
(a
02
b
12
− a
12
b
02
)
. (12.80)
12-325 Polynomial resultants approach
The problem is solved in four steps as illustrated in Solution 12.9. In the first
step, we solve for the first variable X in (12.74) by hiding it as a constant and
homogenizing the equation using a variable W as in (12.81). In the second step, the
Sylvester resultants discussed in Sect. 5-2 on p. 49 or the Jacobian determinant is
obtained as in (12.82). The re sulting determinant (12.83) is solved for X = g(Z)
208 12 Positioning by ranging
and presented in (12.84). The procedure is repeated in steps three and four from
(12.85) to (12.88) to solve for Y = g(Z). The obtained values of X = g(Z) and
Y = g(Z) are substituted in the first expression of (12.53) to give a quadratic
equation in Z. Once this quadratic has been solved for Z, the values of X and Y
are then obtained from (12.84) and (12.88) respectively.
Solution 12.9 (Polynomial resultants solution). Step 1: Solve for X in terms
of Z
f
1
:= (a
02
X + c
02
Z + f
02
)W + b
02
Y
f
2
:= (a
12
X + c
12
Z + f
12
)W + b
12
Y
(12.81)
Step 2: Obtain the Sylvester resultant
J
X
= det
∂f
1
∂Y
∂f
1
∂W
∂f
2
∂Y
∂f
2
∂W
= det
b
02
(a
02
X + c
02
Z + f
02
)
b
12
(a
12
X + c
12
Z + f
12
)
(12.82)
J
X
= b
02
a
12
X + b
02
c
12
Z + b
02
f
12
− b
12
a
02
X − b
12
c
02
Z − b
12
f
02
(12.83)
from (12.83)
X =
{(b
12
c
02
− b
02
c
12
)Z + b
12
f
02
− b
02
f
12
}
(b
02
a
12
− b
12
a
02
)
(12.84)
Step 3: Solve for Y in terms of Z
f
3
:= (b
02
Y + c
02
Z + f
02
)W + b
02
X
f
4
:= (b
12
Y + c
12
Z + f
12
)W + a
12
X
(12.85)
Step 4: Obtain the Sylvester resultant
J
Y
= det
∂f
3
∂X
∂f
3
∂W
∂f
4
∂X
∂f
4
∂W
= det
a
02
(b
02
Y + c
02
Z + f
02
)
a
12
(b
12
Y + c
12
Z + f
12
)
(12.86)
J
Y
= a
02
b
12
Y + a
02
c
12
Z + a
02
f
12
− a
12
b
02
Y − a
12
c
02
Z − a
12
f
02
(12.87)
from (12.87)
Y =
{(a
12
c
02
− a
02
c
12
)Z + a
12
f
02
− a
02
f
12
}
(a
02
b
12
− a
12
b
02
)
(12.88)
Example 12.5 (Three-dimensional ranging to three known stations). Consider dis-
tance measurements of Fig. 13.4 as S
1
= 1324.2380 m, S
2
= 542.2609 m and
S
3
= 430.5286 m, the position of P is obtained using either of the procedures
above as X = 4157066.1116 m, Y = 671429.6655 m and = 4774879.3704 m. Figures
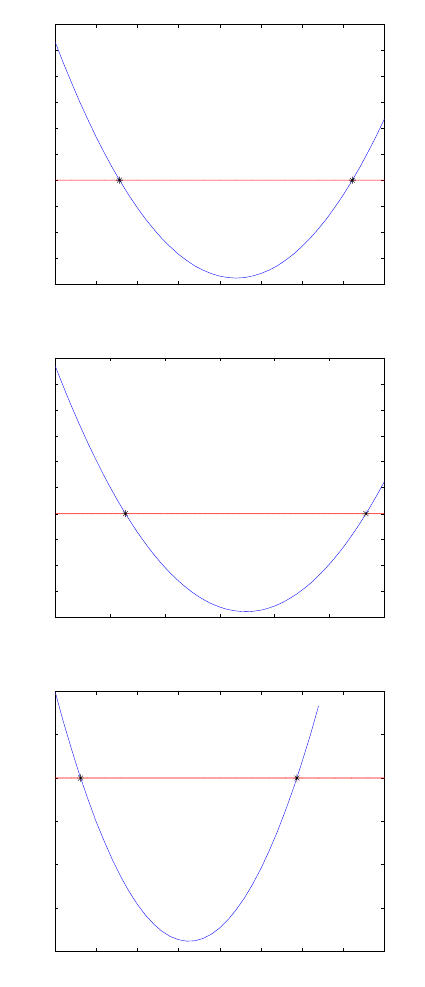
12.14, 12.15 and 12.16 indicate the solutions of {X, Y, Z} respectively. The stars
(intersection of the quadratic curves with the zero line) are the solution points.
The critical configuration of the three-dimensional ranging problem is presented
in Solution 12.10. Equations (12.94) and (12.95) indicate the critical configura-
tion to be the case where points P (X, Y, Z), P
1
(X
1
, Y
1
, Z
1
), P
2
(X
2
, Y
2
, Z
2
), and
P
3
(X
3
, Y
3
, Z
3
) all lie on a plane.
12-3 Ranging by local positioning systems (LPS) 209
4.157 4.157 4.157 4.157 4.157 4.1571 4.1571 4.1571 4.1571
x 10
6
−400
−300
−200
−100
0
100
200
300
400
500
600
Solution of X from Quadratic Equation g
2
X
2
+g
1
X+g
0
=0
X(m)
f(X)
Figure 12.14. Solution of the X coordinates
6.7142 6.7142 6.7143 6.7143 6.7143 6.7143 6.7143
x 10
5
−400
−300
−200
−100
0
100
200
300
400
500
600
Solution of Y from Quadratic Equation f
2
Y
2
+f
1
Y+f
0
=0
Y(m)
f(Y)
Figure 12.15. Solution of the Y coordinates
4.7748 4.7749 4.7749 4.7749 4.7749 4.7749 4.7749 4.7749 4.7749
x 10
6
−400
−300
−200
−100
0
100
200
Solution of Z from Quadratic Equation e
2
Z
2
+e
1
Z+e
0
=0
Z(m)
f(Z)
Figure 12.16. Solution of the Z coordinates
210 12 Positioning by ranging
Solution 12.10 (Critical configuration of three-dimensional ranging).
f
1
(X, Y, Z; X
1
, Y
1
, Z
1
, S
1
) = (X
1
− X)
2
+ (Y
1
− Y )
2
+ (Z
1
− Z)
2
− S
2
1
f
2
(X, Y, Z; X
2
, Y
2
, Z
2
, S
2
) = (X
2
− X)
2
+ (Y
2
− Y )
2
+ (Z
2
− Z)
2
− S
2
2
f
3
(X, Y, Z; X
3
, Y
3
, Z
3
, S
3
) = (X
3
− X)
2
+ (Y
3
− Y )
2
+ (Z
3
− Z)
2
− S
2
3
.
(12.89)
∂f
1
∂X
= −2(X
1
− X),
∂f
2
∂X
= −2(X
2
− X),
∂f
3
∂X
= −2(X
3
− X)
∂f
1
∂Y
= −2(Y
1
− Y ),
∂f
2
∂Y
= −2(Y
2
− Y ),
∂f
3
∂Y
= −2(Y
3
− Y )
∂f
1
∂Z
= −2(Z
1
− Z),
∂f
2
∂Z
= −2(Z
2
− Z),
∂f
3
∂Zv
= −2(Z
3
− Z).
(12.90)
D =
∂f
i
∂X
j
= −8
X
1
− X Y
1
− Y Z
1
− Z
X
2
− X Y
2
− Y Z
1
− Z
X
3
− X Y
3
− Y Z
1
− Z
D ⇔
X
1
− X Y
1
− Y Z
1
− Z
X
2
− X Y
2
− Y Z
1
− Z
X
3
− X Y
3
− Y Z
1
− Z
=
X Y Z 1
X
1
Y
1
Z
1
1
X
2
Y
2
Z
2
1
X
3
Y
3
Z
3
1
= 0.
(12.91)
−
1
8
D = {−Z
1
Y
3
+ Y
1
Z
3
− Y
2
Z
3
+ Y
3
Z
2
− Y
1
Z
2
+ Y
2
Z
1
}X
+ {−Z
1
X
2
− X
1
Z
3
+ Z
1
X
3
+ X
1
Z
2
− X
3
Z
2
+ X
2
Z
3
}Y
+ {Y
1
X
2
− Y
1
X
3
+ Y
3
X
1
− X
2
Y
3
− X
1
Y
2
+ Y
2
X
3
}Z
+X
1
Y
2
Z
3
− X
1
Y
3
Z
2
− X
3
Y
2
Z
1
+ X
2
Y
3
Z
1
− X
2
Y
1
Z
3
+ X
3
Y
1
Z
2
,
(12.92)
thus
X Y Z 1
X
1
Y
1
Z
1
1
X
2
Y
2
Z
2
1
X
3
Y
3
Z
3
1
, (12.93)
describes six times volume of the tetrahedron formed by the points P(X, Y, Z), P
1
(X
1
, Y
1
, Z
1
),
P
2
(X
2
, Y
2
, Z
2
), and P
3
(X
3
, Y
3
, Z
3
) . Therefore
D =
X Y Z 1
X
1
Y
1
Z
1
1
X
2
Y
2
Z
2
1
X
3
Y
3
Z
3
1
a
b
c
d
= 0, (12.94)
results in a system of homogeneous equations
aX + bY + cZ + d = 0
aX
1
+ bY
1
+ cY
1
+ d = 0
aX
2
+ bY
2
+ cZ
2
+ d = 0
aX
3
+ bY
3
+ cZ
3
+ d = 0.
(12.95)
