Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics
Подождите немного. Документ загружается.

12-3 Ranging by local positioning systems (LPS) 191
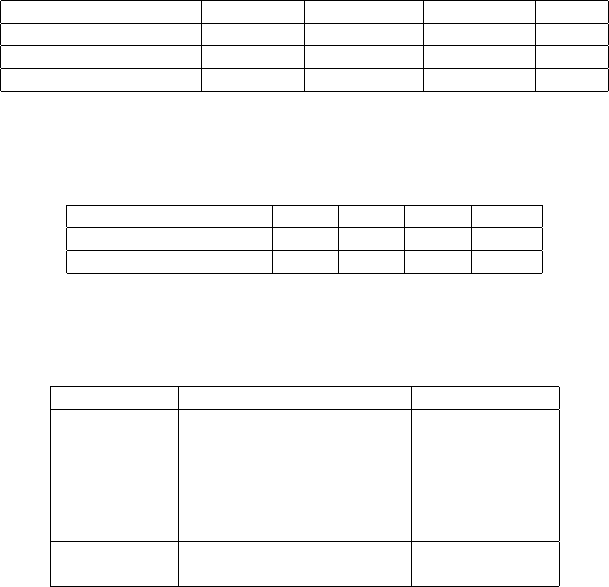
Table 12.8 compares the res ults from the Gauss-Jacobi combinatorial algorithm
and those obtained from least squares approach. Table 12.9 presents the root-
mean-square-errors. In Table 12.10, we present the computed residuals, their sum
of squares and the computed error norm from (12.33). The c omputed error norm
are identical for both procedures. Further comparison of the two procedures will
be given in Chap. 17 where they are used to compute the 7-parameter datum
transformation problem.
Table 12.8. Computed stationary receiver position and range bias
X (m) Y (m) Z (m) cdt(m)
Combinatorial approach 596929.6542 -4847851.5021 4088226.7858 -15.5098
Least squares 596929.6535 -4847851.5526 4088226.7957 -15.5181
Difference 0.0007 0.0505 -0.0098 0.0083
Table 12.9. Computed root-mean-square errors
σ
X
(m) σ
Y
(m) σ
Z
(m) σ
cdt
(m)
Combinatorial Approach 6.4968 11.0141 5.4789 8.8071
Least Squares 34.3769 58.2787 28.9909 46.6018
Table 12.10. Computed residuals, squares of res iduals and error norm
PRN Combinatorial approach (m) Least squares (m)
23 -16.6260 -16.6545
9 -1.3122 -1.3106
5 2.2215 2.2189
1 -16.4369 -16.4675
21 26.8623 26.8311
17 5.4074 5.3825
Sum of squares 1304.0713 1304.0680
Error norm 36.1119 36.1119
12-3 Ranging by local positioning systems (LPS)
As opposed to GPS ranging where the targets being observed are satellites in
space and in motion, Local Positioning Systems’ targets are fixed on the surface
of the Earth as illustrated in Fig. 12.1 on p. 174. We present both planar and
three-dimensional ranging within the LPS system. Planar ranging can be used for
quick point search during engineering and cadastral surveying.
192 12 Positioning by ranging
12-31 Planar ranging
12-311 Conventional approach
Consider two distances {S
1
, S
2
} measured from an unknown station P
0
∈ E
2
to
two known stations P
1
∈ E
2
and P
2
∈ E
2
as shown in Fig. 4.1 in p.34. The two
dimensional distance ranging problem involves the determination of the planar
coordinates {X
0
, Y
0
}
p
0
of the unknown station P
0
∈ E
2
given;
• the observed distances {S
1
, S
2
},
• the planar coordinates {X
1
, Y
1
}
P
1
of station P
1
∈ E
2
and {X
2
, Y
2
}
P
2
of stations
P
2
∈ E
2
.
The nonlinear distance equations relating the given values above with the coordi-
nates of unknown station are expressed (see e.g., (4.1) and (4.2) on p. 33) as
(X
1
− X
0
)
2
+ (Y
1
− Y
0
)
2
= S
2
1
(X
2
− X
0
)
2
+ (Y
2
− Y
0
)
2
= S
2
2
,
(12.34)
which on expanding leads to
X
2
1
+ Y
2
1
− 2X
1
X
0
− 2Y
1
Y
0
+ X
2
0
+ Y
2
0
= S
2
1
X
2
2
+ Y
2
2
− 2X
2
X
0
− 2Y
2
Y
0
+ X
2
0
+ Y
2
0
= S
2
2
.
(12.35)
The conventional analytic approach solves (12.35) by subtracting the first expres-
sion, i.e., (12.35i) from the second one, and expressing one unknown in terms of
the other. This leads to
Y
0
= −
X
1
− X
2
Y
1
− Y
2
X
0
+
S
2
2
− S
2
1
+ X
2
1
− X
2
2
+ Y
2
1
− Y
2
2
2(Y
1
− Y
2
)
, (12.36)
which is substituted for Y
0
in the first expression of (12.35) to give
X
2
1
+ Y
2
1
− 2X
1
X
0
− 2Y
1
−
X
1
− X
2
Y
1
− Y
2
X
0
+
S
2
2
− S
2
1
+ X
2
1
− X
2
2
+ Y
2
1
− Y
2
2
2(Y
1
− Y
2
)
+X
2
0
+
−
X
1
− X
2
Y
1
− Y
2
X
0
+
S
2
2
− S
2
1
+ X
2
1
− X
2
2
+ Y
2
1
− Y
2
2
2(Y
1
− Y
2
)
2
− S
2
1
= 0.
(12.37)
On expanding and factorizing (12.37) leads to

12-3 Ranging by local positioning systems (LPS) 193
(1 + a
2
)X
2
0
+ (2ab − 2X
1
− 2Y
1
a)X
0
+ b
2
− 2Y
1
b + X
2
1
+ Y
2
1
− S
2
1
= 0,
with
a = −
X
1
− X
2
Y
1
− Y
2
and
b =
S
2
2
− S
2
1
+ X
2
1
− X
2
2
+ Y
2
1
− Y
2
2
2(Y
1
− Y
2
)
.
(12.38)
The quadratic equation (12.38) is solved for X
0
using the quadratic formulae (3.8)
or (3.9) on p. 24 and substituted back in (12.36) to give the values of Y
0
.
12-312 Sylvester resultants approach
Whereas the conventional analytical approach presented above involves differenc-
ing, e.g., (12.36), and substitution as in (12.37), the Sylvester resultants technique
discussed in Sect. 5-2 solves (12.35) directly. In-order to achieve this, (12.35) is
first expressed in algebraic form as
g
1
:= X
2
1
+ Y
2
1
− 2X
1
X
0
− 2Y
1
Y
0
+ X
2
0
+ Y
2
0
− S
2
1
= 0
g
2
:= X
2
2
+ Y
2
2
− 2X
2
X
0
− 2Y
2
Y
0
+ X
2
0
+ Y
2
0
− S
2
2
= 0.
(12.39)
Next, the hide variable technique is applied. By hiding the variable Y
0
(i.e., con-
sidering it as a constant), the coefficient matrix of the variable X
0
is formed as
shown in Example 5.2 on p. 50. In (12.39), we note that the polynomials g
1
and
g
2
are both of degree 2 and thus both i and j (e.g., (5.1) on p. 49) are equal to 2
resulting into a (4 × 4) matrix. The coefficient matrix of the variable X
0
formed
by hiding the variable Y
0
(i.e., considering the coefficients of X
0
to be polynomials
in Y
0
) is
A
X
=
1 −2X
1
(Y
2
0
− 2Y
1
Y
0
+ X
2
1
+ Y
2
1
− S
2
1
) 0
0 1 −2X
1
(Y
2
0
− 2Y
1
Y
0
+ X
2
1
+ Y
2
1
− S
2
1
)
1 −2X
2
(Y
2
0
− 2Y
2
Y
0
+ X
2
2
+ Y
2
2
− S
2
2
) 0
0 1 −2X
2
(Y
2
0
− 2Y
2
Y
0
+ X
2
2
+ Y
2
2
− S
2
2
)
,
(12.40)
while that of the variable Y
0
formed by hiding X
0
(i.e., considering the coeffi-
cients of Y
0
to be polynomials in X
0
) is

194 12 Positioning by ranging
A
Y
=
1 −2Y
1
(X
2
0
− 2X
1
X
0
+ X
2
1
+ Y
2
1
− S
2
1
) 0
0 1 −2Y
1
(X
2
0
− 2X
1
X
0
+ X
2
1
+ Y
2
1
− S
2
1
)
1 −2Y
2
(X
2
0
− 2X
2
X
0
+ X
2
2
+ Y
2
2
− S
2
2
) 0
0 1 −2Y
2
(X
2
0
− 2X
2
X
0
+ X
2
2
+ Y
2
2
− S
2
2
)
.
(12.41)
Sylvester resultants are now obtained from the determinants of the coefficient
matrices (12.40) and (12.41) respectively as
Res(g
1
, g
2
, X
0
) = det(A
X
)
Res(g
1
, g
2
, Y
0
) = det(A
Y
),
(12.42)
where Res(g
1
, g
2
, X
0
) and Res(g
1
, g
2
, Y
0
) are the Sylvester resultants of algebraic
equations in (12.39), with respect to the variables X
0
and Y
0
as in (12.40) and
(12.41) respectively. From (12.42) we obtain two quadratic equations (12.43) for
solving the variables X
0
and Y
0
which are the planar coordinates of the unknown
station P
0
. The coefficients of the quadratic equations are given in Solution 12.2.
Solution 12.2 (Sylvester resultants solution of planar coordinates {X
0
, Y
0
}).
a
2
Y
2
0
+ a
1
Y
0
+ a
0
= 0
b
2
X
2
0
+ b
1
X
0
+ b
0
= 0
(12.43)
with the coefficients: a
2
= (4Y
2
2
+ 4X
2
1
− 8Y
1
Y
2
+ 4X
2
2
+ 4Y
2
1
− 8X
2
X
1
).
a
1
= (−4X
2
2
Y
1
− 4S
2
1
Y
2
− 4X
2
1
Y
2
+ 8X
1
X
2
Y
1
+ 4Y
1
S
2
1
+ 4Y
1
Y
2
2
+ 8X
2
X
1
Y
2
− 4Y
3
2
+ 4Y
2
1
Y
2
−
4Y
2
X
2
2
− 4Y
1
S
2
2
− 4Y
3
1
− 4Y
1
X
2
1
+ 4Y
2
S
2
2
).
a
0
= (X
4
2
+Y
4
2
+S
4
2
−4X
2
X
1
Y
2
2
+4X
2
X
1
S
2
2
−4X
1
X
2
Y
2
1
+4X
1
X
2
S
2
1
+2X
2
2
Y
2
2
−2X
2
2
S
2
2
−2Y
2
2
S
2
2
−
4X
1
X
3
2
+6X
2
2
X
2
1
+2X
2
2
Y
2
1
−2X
2
2
S
2
1
+2X
2
1
Y
2
2
−2X
2
1
S
2
2
−2Y
2
1
Y
2
2
+2Y
2
1
S
2
2
+2S
2
1
Y
2
2
−2S
2
1
S
2
2
−4X
2
X
3
1
+
2X
2
1
Y
2
1
− 2X
2
1
S
2
1
− 2Y
2
1
S
2
1
+ X
4
1
+ Y
4
1
+ S
4
1
).
b
2
= (−8Y
1
Y
2
+ 4X
2
1
+ 4Y
2
2
− 8X
2
X
1
+ 4X
2
2
+ 4Y
2
1
).
b
1
= (−4X
3
1
+ 4X
2
S
2
2
+ 8Y
2
Y
1
X
2
− 4X
2
Y
2
2
− 4X
1
Y
2
2
− 4X
1
S
2
2
+ 4X
1
X
2
2
− 4X
2
S
2
1
+ 8Y
1
Y
2
X
1
−
4X
2
Y
2
1
+ 4X
2
X
2
1
− 4X
1
Y
2
1
+ 4X
1
S
2
1
− 4X
3
2
).
b
0
= (4Y
2
Y
1
S
2
2
− 4Y
2
X
2
2
Y
1
− 2Y
2
1
S
2
1
+ X
4
2
+ Y
4
2
+ S
4
2
+ X
4
1
+ Y
4
1
+ S
4
1
− 4Y
1
Y
3
2
+ 4Y
1
S
2
1
Y
2
−
4Y
1
X
2
1
Y
2
+ 2X
2
2
Y
2
2
− 2X
2
2
S
2
2
− 2Y
2
2
S
2
2
− 2X
2
2
X
2
1
+ 2X
2
2
Y
2
1
+ 2X
2
2
S
2
1
+ 2X
2
1
Y
2
2
+ 2X
2
1
S
2
2
+ 6Y
2
1
Y
2
2
−
2Y
2
1
S
2
2
− 2S
2
1
Y
2
2
− 2S
2
1
S
2
2
+ 2X
2
1
Y
2
1
− 2X
2
1
S
2
1
− 4Y
3
1
Y
2
).
12-313 Reduced Groebner basis approach
Reduced Groebner basis (4.38) on p. 45 solves (12.39) directly through

12-3 Ranging by local positioning systems (LPS) 195
GroebnerBasis[{g
1
, g
2
}, {X
0
, Y
0
}, {X
0
}]
GroebnerBasis[{g
1
, g
2
}, {X
0
, Y
0
}, {Y
0
}].
(12.44)
The first expression of (12.44) ensures that one gets a quadratic equation only in
Y
0
with X
0
eliminated, while the second expression ensures a quadratic equation
only in X
0
with Y
0
eliminated. Solution 12.3 presents the results of (12.44).
Solution 12.3 (reduced Groebner basis solution of planar coordinates
{X
0
, Y
0
}).
e
2
Y
2
0
+ e
1
Y
0
+ e
0
= 0
f
2
X
2
0
+ f
1
X
0
+ f
0
= 0
(12.45)
with the coefficients: e
2
= (4X
2
1
− 8X
1
X
2
− 8Y
1
Y
2
+ 4X
2
2
+ 4Y
2
2
+ 4Y
2
1
).
e
1
= (−4X
2
1
Y
1
+ 4S
2
1
Y
1
− 4Y
3
1
− 4X
2
2
Y
2
− 4X
2
1
Y
2
+ 4Y
2
1
Y
2
+ 4Y
1
Y
2
2
− 4Y
3
2
+ 4S
2
2
Y
2
− 4S
2
2
Y
1
−
4S
2
1
Y
2
− 4X
2
2
Y
1
+ 8X
1
X
2
Y
1
+ 8X
1
X
2
Y
2
).
e
0
= (S
4
2
+ 2X
2
1
Y
2
2
+ 4S
2
1
X
1
X
2
+ 4S
2
2
X
1
X
2
− 2S
2
2
X
2
2
− 2Y
2
1
Y
2
2
+ S
4
1
− 2S
2
1
X
2
1
+ X
4
2
+ 2S
2
1
Y
2
2
−
2S
2
1
S
2
2
+ X
4
1
+ Y
4
1
+ 2X
2
2
Y
2
1
− 4X
1
X
2
Y
2
2
+ 6X
2
1
X
2
2
− 2S
2
2
X
2
1
− 2S
2
2
Y
2
2
+ 2X
2
1
Y
2
1
− 2S
2
1
X
2
2
+ 2S
2
2
Y
2
1
−
2S
2
1
Y
2
1
+ 2X
2
2
Y
2
2
− 4X
1
X
3
2
− 4X
1
X
2
Y
2
1
+ Y
4
2
− 4X
3
1
X
2
).
f
2
= (4X
2
1
− 8X
1
X
2
− 8Y
1
Y
2
+ 4X
2
2
+ 4Y
2
2
+ 4Y
2
1
).
f
1
= (−4X
2
Y
2
1
− 4X
1
Y
2
1
+ 4X
2
1
X
2
− 4S
2
2
X
1
− 4X
2
Y
2
2
− 4X
3
1
+ 8X
1
Y
1
Y
2
+ 4S
2
1
X
1
+ 8X
2
Y
1
Y
2
+
4X
1
X
2
2
− 4X
3
2
− 4X
1
Y
2
2
+ 4S
2
2
X
2
− 4S
2
1
X
2
).
f
0
= (S
4
2
+ 2X
2
1
Y
2
2
−4X
2
2
Y
1
Y
2
−2S
2
2
X
2
2
+ 6Y
2
1
Y
2
2
+ 4S
2
1
Y
1
Y
2
+ S
4
1
−4X
2
1
Y
1
Y
2
−2S
2
1
X
2
1
+ ...X
4
2
−
2S
2
1
Y
2
2
− 2S
2
1
S
2
2
+ 4S
2
2
Y
1
Y
2
+ X
4
1
+ Y
4
1
+ 2X
2
2
Y
2
1
− 2X
2
1
X
2
2
+ 2S
2
2
X
2
1
− 4Y
3
1
Y
2
− 2S
2
2
Y
2
2
+ 2X
2
1
Y
2
1
+
2S
2
1
X
2
2
− 2S
2
2
Y
2
1
− 2S
2
1
Y
2
1
+ 2X
2
2
Y
2
2
− 4Y
1
Y
3
2
+ Y
4
2
).
With the given values of known stations and measured distances as listed on
p. 192, all that is required of the practitioner, therefore, is to compute the
coefficients {a
2
, a
1
, a
0
, b
2
, b
1
, b
0
} using the Sylvester resultants Solution 12.2 or
{e
2
, e
1
, e
0
, f
2
, f
1
, f
0
} using the reduced Groebner basis Solution 12.3. Once the
coefficients have been computed, the Matlab, Maple, or Mathematica’s roots com-
mand can be applied to solve the univariate polynomials (12.43) or (12.45) for
the position of the unknown station. The admissible position from the computed
pair of solution is chosen with the help of prior information e.g., from existing
maps. Although the elimination procedure discussed above work, it is also pos-
sible to solve the problem with other direct elimination methods, e.g., Groebner
basis incorporated into “NSolve” or the “solve” command in Matlab’s symbolic
package. Among advantages of using direct elimination in-built functions such as
NSolve are; they remove the issue of figuring out which univariate solutions in
x correspond to which in y (in higher dimensions, or when degree is large, re-
moving this problem saves considerable work), and they also removes room for
mistakes (Lichtblau, Priv. Comm.). We therefore recommend that where possible,
users should directly apply these functions depending on their operating platforms
(Mathematica, Maple or Matlab).
196 12 Positioning by ranging
Example 12.3 (Ranging to two known planar stations). Consider the Example
of [237, p. 240] where two distances {S
1
= 294.330 m, S
2
= 506.420 m} have
been measured from an unknown station P
0
∈ E
2
to two known stations P
1
∈ E
2
and P
2
∈ E
2
(e.g., Fig. 4.1 in p.34). The Cartesian planar coordinates of the two
known stations P
1
and P
2
are given as {X
1
= 328.760 m, Y
1
= 1207.850 m}
P
1
and
{X
2
= 925.040 m, Y
2
= 954.330 m}
P
2
respectively. The planar ranging problem
now involves determining the planar coordinates {X
0
, Y
0
}
p
0
of the unknown sta-
tion P
0
∈ E
2
. Using the given values of known stations and measured distances in
either Solution 12.2 or 12.3, the coefficients {a
2
, a
1
, a
0
, b
2
, b
1
, b
0
} of the quadratic
equation (12.43) or {e
2
, e
1
, e
0
, f
2
, f
1
, f
0
} of (12.45) are computed. Using these co-
efficients and applying Matlab’s roots command (see e.g., (4.42) in Example 4.11
on p. 45) leads to
X
0
= {1336.940, 927.797}m
Y
0
= {593.271, 419.316}m
In a four s tep pro ce dure, [237, p. 240] obtained the values {X
0
(m) = 927.90} and
{Y
0
(m) = 419.42}. The algebraic approaches are however direct and fast (i.e.,
avoids forward and backwards substitutions).
Geometrically, the algebraic curves given by (12.34) would result in a conic inter-
section of two circles with the centers {X
1
, Y
1
} and {X
2
, Y
2
} and radiuses S
1
and
S
2
respectively. The applied polynomial approaches decompose these complicated
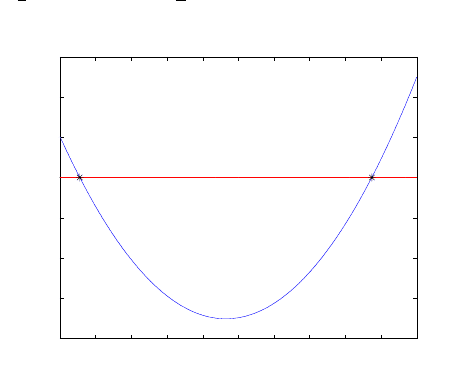
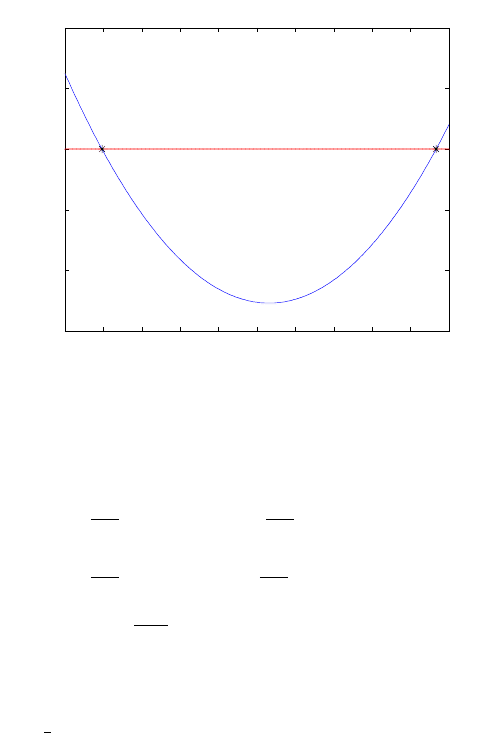
geometries to those of Figs. 12.9 and 12.10 which represent univariate polynomials
and are simpler to solve. Figs. 12.9 and 12.10 indicate the solutions of (12.45) for
the Example presented above. The intersection of the quadratic curves with the
zero line are the solution points. In Solution 12.4, we present the c ritical config-
uration of the planar ranging problem. The computed determinants, (12.51) and
(12.52) indicate the critical configuration (where solution ceases to exist) to be
cases when points P
0
(X, Y ), P
1
(X
1
, Y
1
) and P
2
(X
2
, Y
2
) all lie on a straight line
with gradient −
c
b
and intercept −
a
b
.
900 950 1000 1050 1100 1150 1200 1250 1300 1350 1400
−8
−6
−4
−2
0
2
4
6
x 10
10
Solution of Y from Quadratic Equation e
2
Y
2
+e
1
Y+e
0
=0
Y(m)
f(Y)
Figure 12.9. Solution of the Y coordinates
12-3 Ranging by local positioning systems (LPS) 197
400 420 440 460 480 500 520 540 560 580 600
−1.5
−1
−0.5
0
0.5
1
x 10
10
Solution of X from Quadratic Equation f
2
X
2
+f
1
X+f
0
=0
X(m)
f(X)
Figure 12.10. Solution of the X coordinates
Solution 12.4 (Critical configuration of the planar ranging problem).
f
1
(X, Y ; X
1
, Y
1
, S
1
) = (X
1
− X)
2
+ (Y
1
− Y )
2
− S
2
1
f
2
(X, Y ; X
2
, Y
2
, S
2
) = (X
2
− X)
2
+ (Y
2
− Y )
2
− S
2
2
(12.46)
∂f
1
∂X
= −2(X
1
− X),
∂f
2
∂X
= −2(X
2
− X)
∂f
1
∂Y
= −2(Y
1
− Y ),
∂f
2
∂Y
= −2(Y
2
− Y ),
(12.47)
D =
∂f
i
∂X
j
= 4
X
1
− X X
2
− X
Y
1
− Y Y
2
− Y
D ⇔
X
1
− X X
2
− X
Y
1
− Y Y
2
− Y
=
X Y 1
X
1
Y
1
1
X
2
Y
2
1
= 0,
(12.48)
1
4
D = (X
1
− X)(Y
2
− Y ) − (X
2
− X)(Y
1
− Y )
= X
1
Y
2
− X
1
Y − XY
2
+ XY − X
2
Y
1
+ X
2
Y + XY
1
− XY
= X(Y
1
− Y
2
) + Y (X
2
− X
1
) + X
1
Y
2
− X
2
Y
1
,
(12.49)
thus
X Y 1
X
1
Y
1
1
X
2
Y
2
1
= 2 ×Area of triangle P (X, Y ), P
1
(X
1
, Y
1
), and P
2
(X
2
, Y
2
) (12.50)
D =
X Y 1
X
1
Y
1
1
X
2
Y
2
1
a
b
c
= 0, (12.51)
results in a system of homogeneous equations
aX + bY + c = 0
aX
1
+ bY
1
+ c = 0
aX
2
+ bY
2
+ c = 0.
(12.52)
198 12 Positioning by ranging
12-314 Planar ranging to more than two known stations
In-order to solve the overdetermined two-dimensional ranging problem, the com-
binatorial algorithm is applied. In the first step, combinatorials are formed using
(7.28) on p. 93 and solved in a closed form using either (12.43) or (12.45). In
the second step, the dispersion matrix Σ is obtained from (7.33) on p. 94. Finally
the pseudo-observations are adjusted using linear Gauss-Markov model (see e.g.,
Definition 7.1 on p. 87) in the third step, with the unknown parameters estimated
via Best Linear Uniformly Unbiased Estimator BLUUE (7.12). The dispersion
of the estimated parameters are then obtained using (7.13) on p. 87.
Example 12.4 (Planar ranging to more than two known stations). Let us consider
the example of [237, pp. 240–241] which is also solved in [32]. In this example, the
coordinates of station N are to be determined from distance observations to four
stations P
1
, P
2
, P
3
and P
4
[237, Fig. 6.4.4, p. 229]. In preparation for adjustment,
the distances are corrected and reduced geometrically to Gauss-Krueger projection
and are as given in Table 12.11. Using Gauss-Jacobi combinatorial algorithm, the
coordinates of station N are computed and compared to those of least squares
in [237, p. 242]. From (7.28), six combinations in the minimal sense are formed
and solved for {x, y}
N
for position of station N using either (12.43) or (12.45).
The combinatorial solutions are presented in Table 12.12.
Table 12.11. Distance observations to unknown station N
Pt. Easting Northing s
i
No. x[m] y[m] [m]
1 48177.62 6531.28 611.023
2 49600.15 7185.19 1529.482
3 49830.93 5670.69 1323.884
4 47863.91 5077.24 1206.524
Table 12.12. Position of station N computed for various combinatorials
Combinatorial combinatorial x y
No. points [m] [m]
1 1-2 48565.2783 6058.9770
2 1-3 48565.2636 6058.9649
3 1-4 48565.2701 6058.9702
4 2-3 48565.2697 6058.9849
5 2-4 48565.3402 6058.9201
6 2-5 48565.2661 6058.9731
The adjusted position of the unknown station N is now obtained either by;
(a) simply taking the arithmetic mean of the combinatorial solutions in columns
3 and 4 of Table 12.12 (an approach which does not take into account full
information in terms of the variance-covariance matrix) or,
12-3 Ranging by local positioning systems (LPS) 199
(b) using special linear Gauss-Markov model through the estimation by the Best
Linear Uniformly Unbiased Estimator BLUUE in (7.12). The dispersion of
the estimated parameters are subsequently obtained using (7.13).
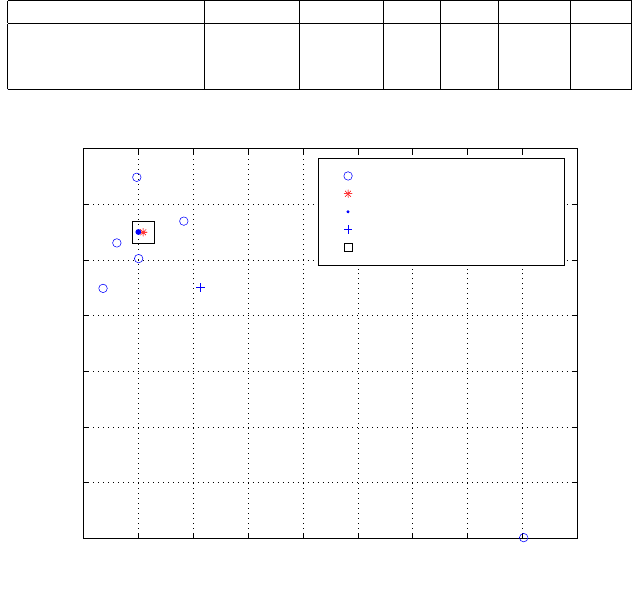
The results are presented in Table 12.13 and plotted in Fig. 12.11. In Table 12.13,
we present the coordinates {x, y} of station N obtained using the least squares
approach in [237], Gauss-Jacobi combinatorial (BLUUE) and the Gauss-Jacobi
combinatorial (arithmetic mean) in columns 2 and 3, with their respective stan-
dard deviations {σ
x
, σ
y
} in columns 4 and 5. In columns 6 and 7, the deviations
{∆
x
, ∆
y
} of the computed coordinates of station N using Gauss-Jacobi combi-
natorial from the least squares’ values of [237] are presented. The deviations of
the exact solutions of each combination (columns 3 and 4 of Table 12.12) from
the adjusted values of Best Linear Uniformly Unbiased Estimator BLUUE (i.e.,
second and third columns of Table 12.13) are plotted in Fig. 12.12.
Table 12.13. Position of station N after adjustments
Approach x(m) y(m) σ
x
(m) σ
y
(m) ∆
x
(m) ∆
y
(m)
Least Squares 48565.2700 6058.9750 0.006 0.006 - -
Gauss-Jacobi (BLUUE) 48565.2709 6058.9750 0.0032 0.0034 -0.0009 0.0000
Gauss-Jacobi (Mean) 48565.2813 6058.9650 - - -0.01133 0.0100
0.06 0.07 0.08 0.09 0.1 0.11 0.12 0.13 0.14 0.15
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
Scattered (X,Y) combinatorial positions around adjusted value
X(m)+48565.2
Y(m)+6058.9
Combinatorial scatter
GJ−Adjusted value
Kahmen and Faig 1988
GJ−Arithmetic mean
Gauss−Jacobi & KF 1988
Figure 12.11. Plot of the position of N from various approaches
From the results in Table 12.13 and Fig. 12.11, we note that when full infor-
mation of the observations is taken into account via the nonlinear error/variance-
covariance propagation, the results of Gauss-Jacobi combinatorial algorithm and
200 12 Positioning by ranging
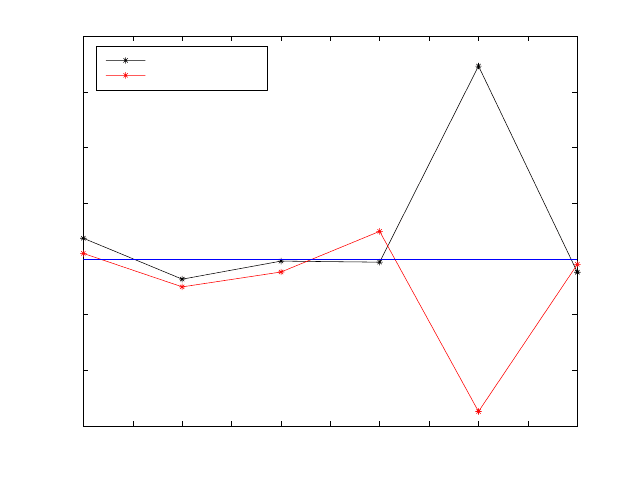
1 1.5 2 2.5 3 3.5 4 4.5 5 5.5 6
−0.06
−0.04
−0.02
0
0.02
0.04
0.06
0.08
Deviation of the Gauss−Jacobi Combinatorial scatter from the adjusted value
Combinatorial number
Deviation in X(m)/Y(m)
Deviation in X
Deviation in Y
Figure 12.12. Deviations of the combinatorial scatter from the BLUUE adjusted posi-
tion of N
least squares from [237] are in the same range. In addition to giving the adjusted
position, Gauss-Jacobi algorithm can accurately pinpoint a poor combinatorial ge-
ometry (e.g., combination 5). This is taken care of through weighting. Fig. 12.11
shows the combinatorial scatter denoted by {◦} and the Gauss-Jacobi combina-
torial adjusted value by {∗}. Least squares estimation from [237] is denoted by
{•} and the arithmetic mean by {+}. One notes that the estimates from Gauss-
Jacobi’s BLUUE {∗} and least squares solution almost coincide. In the Figure,
both estimates are enclosed by {} for clarity purpose. Figure 12.12 indicates the
deviations of the combinatorial scatter from the BLUUE adjusted position of N .
These results indicate the capability of the Gauss-Jacobi combinatorial algorithm
to solve in a closed form the overdetermined planar ranging problems.
12-315 ALESS solution of overdetermined planar ranging problem
Another possibility to solve the overdetermined planar ranging problem is the
ALESS method (see Sect. 7-2), defining the objective function as the sum of the
square residuals of the equations, and considering the necessary condition for the
minimum. The equation for a single measured distance is given by
e
i
= (X
i
− X
0
)
2
+ (Y
i
− Y
0
)
2
− S
2
i
,
