Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics
Подождите немного. Документ загружается.


13-2 Geodetic resection 221
Step 1 (elimination): In this step, the variable y and the term xtan σ are elimi-
nated from the three equations by subtracting the second and third expressions
of (13.5) from the first. This results in
ytanσ(tanT
1
− tanT
2
) = (tanT
2
− tanT
1
)x + (x
1
− x
2
+ y
1
tanT
1
−y
2
tanT
2
)tanσ + x
1
tanT
1
− x
2
tanT
2
− y
1
+ y
2
ytanσ(tanT
1
− tanT
3
) = (tanT
3
− tanT
1
)x + (x
1
− x
3
+ y
1
tanT
1
−y
3
tanT
3
)tanσ + x
1
tanT
1
− x
3
tanT
3
− y
1
+ y
3
.
(13.6)
Step 2 (division): The first expression of (13.6) is divided by (tanT
1
−tanT
2
) and
the second expression by (tanT
1
−tanT
3
). This is done in-order to make ytan σ
appearing on the left-hand-side of both equations the subject of the formula.
The net results are:
ytanσ = −x +
x
1
− x
2
+ y
1
tanT
1
− y
2
tanT
2
tanT
1
− tanT
2
tanσ
+
x
1
tanT
1
− x
2
tanT
2
− y
1
+ y
2
tanT
1
− tanT
2
ytanσ = −x +
x
1
− x
3
+ y
1
tanT
1
− y
3
tanT
3
tanT
1
− tanT
3
tanσ
+
x
1
tanT
1
− x
3
tanT
3
− y
1
+ y
3
tanT
1
− tanT
3
.
(13.7)
Step 3 (elimination): In (13.7), we note that ytan σ and x appear in both expres-
sions. They are eliminated by subtracting the second expression from the first.
On re-arranging the resulting expression leads to tanσ on the left-hand-side
as
tan σ =
N
D
N =
x
1
tanT
1
− x
2
tanT
2
− y
1
+ y
2
tanT
1
− tanT
2
+
x
3
tanT
3
− x
1
tanT
1
− y
3
+ y
1
tanT
1
− tanT
3
D =
x
1
− x
3
+ y
1
tanT
1
− y
3
tanT
3
tanT
1
− tanT
3
+
x
2
− x
1
+ y
2
tanT
2
− y
1
tanT
1
tanT
1
− tanT
2
(13.8)
Step 4 (solution of {x, y}): Once we have solved for σ in (13.8), the first and the
second expressions of (13.5) are re-written in the final step with x, y on the
left-hand-side as
a
11
y + a
12
x = b
11
a
21
y + a
22
x = b
22
,
(13.9)
where;

222 13 Positioning by resection methods
a
11
= (tanT
1
tanσ − 1),
a
12
= (tanT
1
+ tanσ),
a
21
= (tanT
2
tanσ − 1),
a
22
= (tanT
2
+ tanσ),
b
11
= y
1
tanT
1
tanσ − y
1
+ x
1
tanT
1
+ x
1
tanσ,
b
22
= y
2
tanT
2
tanσ − y
2
+ x
2
tanσ + x
2
tanT
2
.
In matrix form, (13.9) is expressed as
a
11
a
12
a
21
a
22
y
x
=
b
11
b
22
, (13.10)
giving the solutions as
y
x
= (a
11
a
22
− a
21
a
12
)
−1
a
22
−a
12
−a
21
a
11
b
11
b
22
(13.11)
or
y = (a
11
a
22
− a
21
a
12
)
−1
(a
22
b
11
− b
22
a
12
)
x = (a
11
a
22
− a
21
a
12
)
−1
(a
11
b
22
− b
11
a
21
)
, (13.12)
which completes the conventional analytic solution.
13-212 Groebner basis approach
Denoting a = tan T
1
, b = tan T
2
, c = tan T
3
, and d = tan σ, (13.5) is simplified
in lexicographic order y > x > d as
f
1
:= −y + ady + ax + xd − y
1
ad − x
1
d − x
1
a + y
1
= 0
f
2
:= −y + bdy + bx + xd − y
2
bd − x
2
d − x
2
b + y
2
= 0
f
3
:= −y + cdy + cx + xd − y
3
cd − x
3
d − x
3
c + y
3
= 0.
(13.13)
The reduced Groebner basis (4.38) on p. 45 is then computed as
GroebnerBasis [{f
1
, f
2
, f
3
}, {x, y, d}, {x, y}]
GroebnerBasis [{f
1
, f
2
, f
3
}, {x, y, d}, {y}]
GroebnerBasis [{f
1
, f
2
, f
3
}, {x, y, d}, {x}].
(13.14)
The first expression of (13.14) gives a linear equation in the variable d allowing
the computation of the unknown orientation paramete r σ. The second and the
third expressions respectively give linear equations in x and y in the variable d.
The computed reduced Groebner basis re-arranged with the unknown te rms on
the left-hand-side are presented in Solution 13.1.

13-2 Geodetic resection 223
Solution 13.1 (reduced Groebner basis computation of planar resec-
tion).
d =
N1
D1
x = −
N2
(−cd
2
+ a − c + ad
2
)
y = −
N3
(b −c + bd
2
− cd
2
)
,
(13.15)
where
N1 = −(abX
1
− acX
1
+ aY
2
− abX
2
+ bcX
2
− aY
3
+ acX
3
−bcX
3
− bY
1
+ cY
1
− cY
2
+ bY
3
)
D1 = (bX
1
− aX
2
+ aX
3
− bX
3
+ abY
1
− acY
1
− cX
1
− abY
2
+bcY
2
+ cX
2
+ acY
3
− bcY
3
),
N2 =
(−adY
1
− cdY
1
+ acd
2
Y
1
− Y
3
− aX
1
− dX
1
+ acdX
1
+ cd
2
X
1
+cX
3
+ dX
3
− acdX
3
− ad
2
X
3
+ Y
1
+ adY
3
+ cdY
3
− acd
2
Y
3
)
and
N3 =
(−bcX
2
− bdX
2
− cdX
2
− d
2
X
2
+ bcX
3
+ bdX
3
+ cdX
3
+ d
2
X
3
+cY
2
+ dY
2
− bcdY
2
− bd
2
Y
2
− bY
3
− dY
3
+ bcdY
3
+ cd
2
Y
3
).
Once d has been computed from the first expression of (13.15), it is inserted into
the second and third expressions to solve the unknowns {x, y} respec tively. The
unknown orientation in the horizontal plane is then computed via σ = tan
−1
d.
13-213 Sturmfels’ resultant approach
Let z be a homogenizing variable for (13.13). In-order to s olve for the variable d
in (13.13), we hide d by making it a polynomial of degree zero (i.e., treating it as
a constant) as
g
1
:= −y + ady + ax + dx + (−y
1
ad − x
1
d − x
1
a + y
1
)z= 0
g
2
:= −y + bdy + bx + dx + (−y
2
bd − x
2
d − x
2
b + y
2
)z= 0
g
3
:= −y + cdy + cx + dx + (−y
3
cd − x
3
d − x
3
c + y
3
)z= 0,
(13.16)
which is expressed in the form (5.12) as
J
d
= det
∂g
1
∂x
∂g
1
∂y
∂g
1
∂z
∂g
2
∂x
∂g
2
∂y
∂g
2
∂z
∂g
3
∂x
∂g
3
∂y
∂g
3
∂z
= det
(a + d) (ad − 1) (y
1
− y
1
ad −x
1
d −x
1
a)
(b + d) (bd −1) (y
2
− y
2
bd −x
2
d −x
2
b)
(c + d) (cd −1) (y
3
− y
3
cd −x
3
d −x
3
c)
. (13.17)
Equation (13.17) leads to

224 13 Positioning by resection methods
e
3
d
3
+ e
2
d
2
+ e
1
d + e
0
= 0 ,
with
e
3
= ax
3
− bx
3
− ay
2
b −ax
2
+ cx
2
− cx
1
+ cy
2
b + ay
3
c −cy
1
a + bx
1
+ by
1
a −by
3
c
e
2
= cy
1
− ax
2
b + ay
2
+ ax
3
c −by
1
− ay
3
+ bx
1
a + by
3
+ cx
2
b −cy
2
− cx
1
a −bx
3
c
e
1
= ax
3
− bx
3
− ay
2
b −ax
2
+ cx
2
− cx
1
+ cy
2
b + ay
3
c −cy
1
a + bx
1
+ by
1
a −by
3
c
e
0
= cy
1
− ax
2
b + ay
2
+ ax
3
c −by
1
− ay
3
+ bx
1
a + by
3
+ cx
2
b −cy
2
− cx
1
a −bx
3
c.
(13.18)
The value of d is then solved from (13.18) using Matlab’s roots command (see
4.42 on p. 46). Comparing the expressions for d in (13.15) and (13.18), we note
that the reduced Groebner basis in Solution 13.1 gave a linear function while
the Sturmfels’ approach results in a cubic polynomial. Both expressions however
lead to the same numerical results. The advantage of reduced Groebner basis over
the Sturmfels’ approach, however, is that the solution is uniquely determined.
Sturmfels’ approach requires prior information to choose the admissible value of d
from the three solutions. Once this value has been selected, the coordinates {x, y}
are then solved in terms of d as follows:
1. Hiding x and solving in terms of d from (f
1
, f
2
) of (13.13) gives
h
1
:= (ad − 1)y + (ax + dx − y
1
ad − x
1
d − x
1
a + y
1
)z= 0
h
2
:= (bd − 1)y + (bx + dx − y
2
bd − x
2
d − x
2
b + y
2
)z= 0.
(13.19)
Applying (5.12) leads to
J
x
= det
∂h
1
∂y
∂h
1
∂z
∂h
2
∂y
∂h
2
∂z
= det
(ad −1) (ax + dx −y
1
ad −x
1
d −x
1
a + y
1
)
(bd −1) (bx + dx − y
2
bd −x
2
d −x
2
b + y
2
)
.
(13.20)
The Jacobian determinant of (13.20) is
x = −(y
1
+ ady
2
− ad
2
y
2
b −ad
2
x
2
− adx
2
b + x
1
abd −y
2
+ y
2
bd + x
2
d
+x
2
b + y
1
ad
2
b −y
1
ad −y
1
bd −x
1
d −x
1
a + x
1
d
2
b)/(a + ad
2
− b − d
2
b).
(13.21)
2. Hiding y and solving in terms of d from (f
2
, f
3
) of (13.13) gives
k
1
:= (b + d)x + (bdy − y − y
2
bd − x
2
d − x
2
b + y
2
)z= 0
k
2
:= (c + d)x + (cdy − y − y
3
cd − x
3
d − x
3
c + y
3
)z= 0,
(13.22)
whose Jacobian determinant

13-2 Geodetic resection 225
J
y
= det
∂k
1
∂x
∂k
1
∂z
∂k
2
∂x
∂k
2
∂z
= det
(b + d) (bdy − y − y
2
bd −x
2
d −x
2
b + y
2
)
(c + d) (cdy − y − y
3
cd −x
3
d −x
3
c + y
3
)
. (13.23)
leads to
y = −(−y
2
d + by
3
− by
3
cd −bx
3
d −bx
3
c + x
2
bc + dy
3
− y
3
cd
2
− x
3
d
2
−dx
3
c + y
2
bdc + y
2
bd
2
− y
2
c + x
2
d
2
+ x
2
bd + x
2
dc)/(−bd
2
− b + cd
2
+ c)
(13.24)
Once d has been computed from ((13.18), it is used in (13.21) and (13.24) to obtain
x and y respectively. The unknown orientation in the horizontal plane can now be
computed via σ = tan
−1
d.
Example 13.1. Let us consider the Example given by [237, p. 234] with our axis
defined such that the Easting refer to the Y −axis and the Northing refer to the
X−axis. The input data are given in Table 13.1 for the coordinates of three known
stations A, B and M which are denoted by P
1
, P
2
and P
3
respectively in Fig. 13.3.
Table 13.2 gives directional observations T
i
| i ∈ {1, 2, 3} from the observing un-
known station P ∈ E
2
(whose unknown x, y coordinates and orientation parameter
σ are sought) to three known stations P
i
∈ E
2
| i ∈ {1, 2, 3} whose coordinates
X
i
, Y
i
| i ∈ {1, 2, 3} are given in Table 13.1. The obtained results from either re-
duced Groebner basis or Sturmfels’ resultant algebraic approaches are presented
in Table 13.3. They are identical to those of [237, p. 234] once we interchange the
axes. If Sturmfels’ solution is adopted in (13.18), two complex and one real values
of d are obtained. The real value, which is identical to that obtained from reduced
Groebner basis s olution (13.15) is used to solve for σ from σ = tan
−1
d.
Table 13.1. Coordinates of known stations P
i
∈ E
2
| i ∈ {1, 2, 3}
Station Easting Northing
Y (m) X(m)
P
1
46867.94 5537.00
P
2
51293.86 6365.89
P
3
49666.56 4448.58
Table 13.2. Directions measured from unknown station P ∈ E
2
to known stations
P
i
∈ E
2
| i ∈ {1, 2, 3}
Station Horizontal directions
◦ 0 00
P
1
60 07 50
P
2
265 18 22
P
3
326 33 59

226 13 Positioning by resection methods
Table 13.3. Position and orientation of station P ∈ E
2
.
Station Easting Northing Orientation unknown
Y (m) X(m)
◦ 0 00
P 48613.3384 6361.1690
σ 4 35 34.7
13-22 Three-dimensional resection
13-221 Exact solution
Closed form solution of three-dimensional resection problem concerns itself with
the determination of position and orientation of a p oint P connected by angular ob-
servations of type horizontal directions T
i
and vertical directions B
i
to three known
stations P
1
, P
2
, P
3
(see e.g., Fig. 13.4 on p. 227). From these angular measure-
ments, distances are derived by solving equations known as Grunert’s equations.
Once the distances have been established, the unknown position P is determined
using ranging techniques that we disc ussed in Sect. 12-32 of Chap. 12. The closed
form solution of the three-dimensional resec tion problem is completed by solving
the unknown orientation parameters that relate the global reference frame F
•
to
the local level reference frame of type F
∗
. As we have already p ointed out in Sect.
13-1, several procedures have been suggested for solving Grunert’s equations. This
section presents three alternative algebraic methods for solving explicitly the three-
dimensional resection problem namely; Groebner basis, polynomial resultants and
Grafarend-Lohse-Schaffrin methods.
13-222 Solution of Grunert’s distance equations
We begin in Solution 13.2 by deriving Grunert’s distance equations. These equa-
tions relate;
(i) known distances S
ij
, i, j = 1, 2, 3 |i 6= j computed from known stations,
(ii) unknown distances S
i
, i = 1, 2, 3 between the unknown station P ∈ E
3
, and
three known stations P
i
∈ E
3
| i ∈ {1, 2, 3} and
(iii) the spatial angles ψ
ij
, i, j = 1, 2, 3 |i 6= j derived from measured horizontal
directions T
i
and vertical directions B
i
in the local level reference frame F.
∗
In Solution 13.2, multiplying (10.11) on p. 145 by (13.25) leads to (13.26). Af-
ter manipulations of (13.27),(13.28) and (13.29), space angles ψ
ij
can be written
in terms of spherical coordinates {T
i
, B
i
}, {T
j
, B
j
} of points P
i
and P
j
with re-
spect to a theodolite orthogonal Euclidean frame F
∗
as in (13.30). The Grunert’s
equations for the three unknown distances S
1
, S
2
, S
3
are then written in terms
of known distances S
12
, S
23
, S
31
and space angles ψ
12
, ψ
23
, ψ
31
(illustrated in Fig.
13.4) as in (13.32). Solution of (13.32) was first proposed by J. A. Grunert [194].
Procedures that were later developed sought to optimize the solution of (13.32) in
terms of computational steps. In particular, the interest was to reduce the order
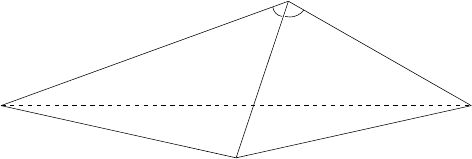
13-2 Geodetic resection 227
P
2
P
3
S
3
P
S
2
S
31
ψ
12
ψ
23
P
1
S
1
S
12
S
23
Figure 13.4. Geometrical interpretation of the 3D resection
of the univariate polynomial that resulted following the solution of (13.32). Such
procedures were encountered in Sect. 13-1. In what follows, we present algebraic
solution of (13.32).
Solution 13.2 (Derivation of Grunert’s distance equations).
(−2) [cos T
j
cos B
j
, sin T
j
cos B
j
, sin B
j
] S
j
(13.25)
(−2)[cosT
j
cosB
j
, sinT
j
cosB
j
, sinB
j
]S
i
S
j
cosT
i
cosB
i
sinT
i
cosB
i
sinB
i
=
(−2)[(X
j
− X), (Y
j
− Y ), (Z
j
− Z)]
X
i
− X
Y
i
− Y
Z
i
− Z
(13.26)
(X
j
− X)(X
i
− X) = X
j
X
i
− X
j
X − X
i
X + X
2
(X
i
− X
j
)(X
i
− X
j
) = X
2
i
− 2X
i
X
j
+ X
2
j
(X
i
− X)(X
i
− X) = X
2
i
− 2X
i
X + X
2
(X
j
− X)(X
j
− X) = X
2
j
− 2X
j
X + X
2
⇒
⇒ (X
i
− X
j
)
2
− (X
i
− X)
2
− (X
j
− X)
2
= −2(X
j
− X)(X
i
− X)
(13.27)
(−2)[cosT
j
cosB
j
, sinT
j
cosB
j
, sinB
j
]S
i
S
j
cosT
i
cosB
i
sinT
i
cosB
i
sinB
i
=
(X
i
− X
j
)
2
+ (Y
i
− Y
j
)
2
+ (Z
i
− Z
j
)
2
−
−(X
i
− X)
2
− (Y
i
− Y )
2
− (Z
i
− Z)
2
−
−(X
j
− X)
2
− (Y
j
− Y )
2
− (Z
j
− Z)
2
(13.28)
−2 {sin B
j
sin B
i
+ cos B
j
cos B
i
cos(T
j
− T
i
)}S
i
S
j
=
=
(X
i
− X
j
)
2
+ (Y
i
− Y
j
)
2
+ (Z
i
− Z
j
)
2
−
−(X
i
− X)
2
− (Y
i
− Y )
2
− (Z
i
− Z)
2
−
−(X
j
− X)
2
− (Y
j
− Y )
2
− (Z
j
− Z)
2
(13.29)
cos ψ
ij
= cos B
i
cos B
j
cos(T
j
− T
i
) + sin B
i
sin B
j
(13.30)
−2 cos ψ
ij
S
i
S
j
= S
2
ij
− S
2
i
− S
2
j
S
2
ij
= S
2
i
+ S
2
j
− 2S
i
S
j
cos ψ
ij
(13.31)

228 13 Positioning by resection methods
S
2
12
= S
2
1
+ S
2
2
− 2S
1
S
2
cos ψ
12
S
2
23
= S
2
2
+ S
2
3
− 2S
2
S
3
cos ψ
23
S
2
31
= S
2
3
+ S
2
1
− 2S
3
S
1
cos ψ
31
(13.32)
13-223 Groebner basis solution of Grunert’s equations
In-order to quicken our understanding of the application of Groebner basis to s olve
Grunert’s distance equations (13.32), let us consider a simple case of a regular
tetrahedron. A regular tetrahedron presents a unique case where all the distances
and spatial angles of Fig. 13.4 are equal. Instead of computing Groebner basis
using 4.36 on p. 45, we will demonstrate by a hand computation how Groebner
basis can be computed. Later, we will apply (4.36) to solve the general case of
(13.32). We begin by expressing (13.32) in algebraic form
x
2
1
− 2a
12
x
1
x
2
+ x
2
2
− a
0
= 0
x
2
2
− 2b
23
x
2
x
3
+ x
2
3
− b
0
= 0
x
2
1
− 2c
31
x
1
x
3
+ x
2
3
− c
0
= 0,
(13.33)
where the unknown distances {S
1
, S
2
, S
3
} that appear in (13.32) are denoted by
{x
1
, x
2
, x
3
}. The distances between known stations {S
12
, S
23
, S
31
} are denoted by
{a
o
, b
o
, c
o
}, while the constants {a
12
, b
23
, c
31
} represent {cos ψ
12
, cos ψ
23
, cos ψ
31
}
respectively. Equation (13.33) therefore has only the distances {x
1
, x
2
, x
3
} as un-
knowns. These are the distances relating the unknown station P
0
to the known
stations P
i
|
{i=1,2,3}
. Grafarend [187] dem onstrated that for each of the quadratic
equation in (13.33), there exists an elliptical cylinder in the planes {x
1
, x
2
},
{x
2
, x
3
} and {x
3
, x
1
} for the first, second and third equations respectively. These
cylinders are constrained to their first quadrant since the distances are positive
thus {x
1
∈ R
+
}, {x
2
∈ R
+
} and {x
3
∈ R
+
}. For a regular te trahedron, the dis-
tances x
1
= x
2
= x
3
joining the unknown station P ∈ E
3
to three known stations
P
i
∈ E
3
|
{i=1,2,3}
are all equal to the distances S
12
= S
23
= S
31
between the known
stations. Let us give these distances a value +
√
d. The spatial angles are also equal
(i.e., ψ
12
= ψ
23
= ψ
31
= 60
◦
). In Solution 13.3, a hand computation of Groebner
basis of (13.33) is carried out and used to find the Grunert’s distances for the
regular tetrahedron (i.e., show that the desired solutions for {x
1
, x
2
, x
3
} ∈ R
+
are
x
1
= x
2
= x
3
= +
√
d.)
Solution 13.3 (Hand computation of Groebner basis of (13.32) for a reg-
ular tetrahedron). For a regular tetrahedron, where ψ
ij
= 60
◦
, and a
0
= b
0
= c
0
= d,
(13.33) is re-written in lexicographic order x
1
> x
2
> x
3
as
x
2
1
− x
1
x
2
+ x
2
2
− d = 0
x
2
2
− x
2
x
3
+ x
2
3
− d = 0
x
2
1
− x
1
x
3
+ x
2
3
− d = 0,
(13.34)
giving rise to the Ideal I (e.g., 4.14 on p. 37) as
I =
x
2
1
− x
1
x
2
+ x
2
2
− d, x
2
2
− x
2
x
3
+ x
2
3
− d, x
2
1
− x
1
x
3
+ x
2
3
− d
⊂ R [x
1
, x
2
, x
3
] ,
(13.35)
13-2 Geodetic resection 229
whose generators G are
g
1
= x
2
1
− x
1
x
2
+ x
2
2
− d
g
2
= x
2
1
− x
1
x
3
+ x
2
3
− d
g
3
= x
2
2
− x
2
x
3
+ x
2
3
− d.
(13.36)
Desired now are the Groebner basis (simplified structure) of the generators
(13.36) of the Ideal I in (13.35). Using (4.23) on p. 41, the S pair polynomi-
als (g
1
, g
2
), (g
1
, g
3
), (g
2
, g
3
) are computed from the generators (13.36). From B.
Buchberger’s third criterion explained in Chap. 4, we notice that LM(g
2
) = x
2
1
divides the LCM(g
1
, g
3
) = x
2
1
x
2
2
. One therefore suppresses (g
1
, g
3
) and considers
only (g
1
, g
2
), (g
2
, g
3
) instead. S(g
1
, g
2
) gives
S(g
1
, g
2
) = −x
1
x
2
+ x
1
x
3
+ x
2
2
− x
2
3
, (13.37)
which is reduced with respect to G by subtracting g
3
to obtain
− x
1
x
2
+ x
1
x
3
− 2x
2
3
+ x
2
x
3
+ d. (13.38)
Equation (13.38) does not reduce to zero and is added to the original list G of the
generating set of the Ideal I as g
4
. The S–polynomial pairs to be considered next
are S(g
2
, g
3
), S(g
2
, g
4
) and S(g
3
, g
4
) from the new generating set G = {g
2
, g
3
, g
4
}.
Since LM (g
2
) and LM(g
3
) are relatively prime, S(g
2
, g
3
) reduces to ze ro modulo G
(S(g
2
, g
3
) →
G
0). The S pair polynomials remaining for consideration are (g
2
, g
4
)
and (g
3
, g
4
). S(g
2
, g
4
) gives
S(g
2
, g
4
) = x
2
1
x
3
+ x
1
d − 2x
1
x
2
3
+ x
2
x
2
3
− x
2
d, (13.39)
which is reduced with respect to G by subtracting x
3
g
2
to give
x
1
d − x
1
x
2
3
+ x
2
x
2
3
− x
2
d − x
3
3
+ x
3
d, (13.40)
Equation (13.40) does not reduce to zero and is added to the list G of the generating
set of the Ideal I as g
5
. The S–polynomial pair to be considered next is S(g
3
, g
4
)
from the new generating set G = {g
2
, g
3
, g
4
, g
5
} . S(g
3
, g
4
) gives
S(g
3
, g
4
) = −x
1
x
2
3
+ x
1
d + 2x
2
x
2
3
− x
2
2
x
3
− x
2
d, (13.41)
which is reduced with respect to G by subtracting g
5
and adding x
3
g
3
to give
2x
3
3
− 2x
3
d. (13.42)
Equation (13.42) is a univariate polynomial and completes the solution of the set
G of Groebner basis summarized as
G :=
g
2
= x
2
1
− x
1
x
3
+ x
2
3
− d
g
3
= x
2
2
− x
2
x
3
+ x
2
3
− d
g
4
= −x
1
x
2
+ x
1
x
3
− 2x
2
3
+ x
2
x
3
+ d
g
5
= x
1
d − x
1
x
2
3
+ x
2
x
2
3
− x
2
d − x
3
3
+ x
3
d
g
6
= 2x
3
3
− 2x
3
d.
(13.43)

230 13 Positioning by resection methods
From the computed Groebner basis in (13.43), one notes that the element g
6
=
2x
3
3
− 2x
3
d is a cubic polynomial in x
3
and readily gives the values of x
3
=
n
0 , ±
√
d
o
. The solutions to the Grunert’s distance equations (13.33) for a reg-
ular tetrahedron are then deduced as follows: Since S
3
= x
3
∈ R
+
, the value
of S
3
= +
√
d. This is substituted back in g
3
= x
2
2
− x
2
x
3
+ x
2
3
− d and
g
2
= x
2
1
− x
1
x
3
+ x
2
3
− d to give x
2
=
n
0 , +
√
d
o
and x
1
=
n
0 , +
√
d
o
respec-
tively. This completes the solution of Grunert’s distance equations (13.33) for the
unknown distances x
1
= x
2
= x
3
= +
√
d as we had initially assumed.
Having demonstrated a hand computation of Groebner basis of the Grunert’s
distance equations (13.32) for a regular tetrahedron, let us consider next the gen-
eral case. The geometry of the three-dimensional resection problem in practice is
hardly a regular tetrahedron. Beginning by expressing (13.32) algebraically as
g
1
:= x
2
1
+ x
2
2
+ a
12
x
1
x
2
+ a
0
= 0
g
2
:= x
2
2
+ x
2
3
+ b
23
x
2
x
3
+ b
0
= 0
g
3
:= x
2
3
+ x
2
1
+ c
31
x
3
x
1
+ c
0
= 0,
(13.44)
where
S
1
= x
1
∈ R
+
, S
2
= x
2
∈ R
+
, S
3
= x
3
∈ R
+
,
−2 cos ψ
12
= a
12
, −2 cos ψ
23
= b
23
, −2 cos ψ
31
= c
31
,
−S
2
12
= a
0
, −S
2
23
= b
0
, −S
2
31
= c
0
,
(13.45)
one forms the Ideal
I =< x
2
1
+ x
2
2
+ a
12
x
1
x
2
+ a
0
, x
2
2
+ x
2
3
+ b
23
x
2
x
3
+ b
0
, x
2
3
+ x
2
1
+ c
31
x
3
x
1
+ c
0
> . (13.46)
We then seek the Groebner basis of the generators of the Ideal (13.46). Following
lexicographic ordering {x
1
> x
2
> x
3
}, (4.36) on p. 45 is applied as
GroebnerBasis[{g
1
, g
2
, g
3
}, {x
1
, x
2
, x
3
}], (13.47)
giving the Groebner basis of the Ideal (13.46) expressed in [27, Boxes 3-3a and
3-3b]. Distances can also be derived from (13.44) using reduced Groebner basis.
We leave it as an exercise for the reader to try and solve the unknown distances
{x
1
, x
2
, x
3
} in (13.44) using reduced Groebner basis (4.38) on p. 45.
13-224 Polynomial resultants’ solution of Grunert’s distance equations
Besides the use of Groebner bases approach demonstrated above, polynomial re-
sultants techniques can also be used to solve Grunert’s equations for distances.
We illustrate the solution of the problem using F. Macaulay formulation of Sect.
5-31 and B. Sturmfels’ formulation presented in Sect. 5-32. We start by expressing
(13.44) as
R
1
:= x
2
1
+ x
2
2
+ a
12
x
1
x
2
+ a
0
= 0
R
2
:= x
2
2
+ x
2
3
+ b
23
x
2
x
3
+ b
0
= 0
R
3
:= x
2
1
+ x
2
3
+ c
31
x
1
x
3
+ c
0
= 0.
(13.48)
