Awange J.,Grafarend E., Palancz B., Zaletnyik P. Algebraic Geodesy and Geoinformatics
Подождите немного. Документ загружается.


13-2 Geodetic resection 231
Clearly, (13.48) is not homogeneous (see Definition 5.1 on p. 49). It is therefore
homogenized by introducing the fourth variable x
4
and treating the variable which
is to be solved, say x
1
, as a constant (i.e., hiding it by giving it degree zero). The
resulting homogenized polynomial is
R
11
:= x
2
2
+ a
12
x
1
x
2
x
4
+ (a
0
+ x
2
1
)x
2
4
= 0
R
21
:= x
2
2
+ x
2
3
+ b
23
x
2
x
3
+ b
0
x
2
4
= 0
R
31
:= x
2
3
+ c
31
x
1
x
3
x
4
+ (x
2
1
+ c
0
)x
2
4
= 0,
(13.49)
which is simplified as
R
11
:= x
2
2
+ a
1
x
2
x
4
+ a
2
x
2
4
= 0
R
21
:= x
2
2
+ x
2
3
+ b
1
x
2
x
3
+ b
2
x
2
4
= 0
R
31
:= x
2
3
+ c
1
x
3
x
4
+ c
2
x
2
4
= 0,
(13.50)
with the coefficients denoted as a
1
= a
12
x
1
, a
2
= (a
0
+x
2
1
), b
1
= b
23
, b
2
= b
0
, c
1
=
c
31
x
1
, c
2
= (c
0
+ x
2
1
).
Approach 1 (F. Macaulay Formulation):
The first step involves the determination of the total degree of (13.50) using (5.7)
on p. 52 which gives d = 4. In the second step, one formulates the general set com-
prising the monomials of degree 4 in three variables by multiplying the monomials
of (13.50) by each other. These monomials form the elements of the set X
d
(e.g.,
5.8 on p. 52) as
X
d
=
x
4
2
, x
3
2
x
4
, x
2
2
x
2
3
, x
3
2
x
3
, x
2
2
x
2
4
, x
2
2
x
3
x
4
, x
2
x
3
3
x
2
x
3
4
, x
2
x
2
3
x
4
, x
2
x
3
x
2
4
, x
2
3
x
2
4
, x
3
x
3
4
, x
4
4
, x
4
3
, x
3
3
x
4
, (13.51)
which is now partitioned in step 3 according to (5.9) on p. 52 as
X
d
i
= {x
α
| α
i
≥ d
i
and α
j
< d
j
, ∀
j
< i}
X
4
2
= {x
4
2
, x
3
2
x
4
, x
2
2
x
2
3
, x
3
2
x
3
, x
2
2
x
2
4
, x
2
2
x
3
x
4
}
X
4
3
= {x
2
x
2
3
x
4
, x
2
3
x
2
4
, x
2
x
3
3
, x
4
3
, x
3
3
x
4
}
X
4
4
= {x
2
x
3
4
, x
2
x
3
x
2
4
, x
3
x
3
4
, x
4
4
}.
(13.52)
In the fourth step, the polynomials F
i
are formed using the sets in (13.52) according
to (5.10) on p. 53 giving rise to
F
1
:=
X
4
2
x
2
2
f
1
= {x
2
2
f
1
, x
2
x
4
f
1
, x
2
3
f
1
, x
2
x
3
f
1
, x
2
4
f
1
, x
3
x
4
f
1
}
F
2
:=
X
4
3
x
2
3
f
2
= {x
2
x
4
f
2
, x
2
4
f
2
, x
2
x
3
f
2
, x
2
3
f
2
, x
3
x
4
f
2
}
F
3
:=
X
4
4
x
2
4
f
3
= {x
2
x
4
f
3
, x
2
x
3
f
3
, x
3
x
4
f
3
, x
2
4
f
3
}.
(13.53)

232 13 Positioning by resection methods
Finally, the matrix A of dimension (15 × 15) is formed as discussed on p. 53. Its
rows are the c oefficients of the f
i
in (13.53) and the columns are the monomials
{c
1
= x
4
2
, c
2
= x
3
2
x
3
, c
3
= x
3
2
x
4
, c
4
= x
2
2
x
2
3
, c
5
= x
2
2
x
3
x
4
, c
6
= x
2
2
x
2
4
, c
7
= x
2
x
3
3
,
c
8
= x
2
x
2
3
x
4
, c
9
= x
2
x
3
x
2
4
, c
10
= x
2
x
3
4
, c
11
= x
4
3
, c
12
= x
3
3
x
4
, c
13
= x
2
3
x
2
4
,
c
14
= x
3
x
3
4
and c
15
= x
4
4
},
elements of the sets formed in (13.52). The matrix A is
A =
c
1
c
2
c
3
c
4
c
5
c
6
c
7
c
8
c
9
c
10
c
11
c
12
c
13
c
14
c
15
x
2
2
f
1
1 0 a
1
0 0 a
2
0 0 0 0 0 0 0 0 0
x
2
3
f
1
0 0 0 1 0 0 0 a
1
0 0 0 0 a
2
0 0
x
2
x
3
f
1
0 1 0 0 a
1
0 0 0 a
2
0 0 0 0 0 0
x
2
4
f
1
0 0 0 0 0 1 0 0 0 a
1
0 0 0 0 a
2
x
3
x
4
f
1
0 0 0 0 1 0 0 0 a
1
0 0 0 0 a
2
0
x
2
x
4
f
1
0 0 1 0 0 a
1
0 0 0 a
2
0 0 0 0 0
x
2
x
4
f
2
0 0 1 0 b
1
0 0 1 0 b
2
0 0 0 0 0
x
2
4
f
2
0 0 0 0 0 1 0 0 b
1
0 0 0 1 0 b
2
x
2
3
f
2
0 0 0 1 0 0 b
1
0 0 0 1 0 b
2
0 0
x
3
x
4
f
2
0 0 0 0 1 0 0 b
1
0 0 0 1 0 b
2
0
x
2
x
3
f
2
0 1 0 b
1
0 0 1 0 b
2
0 0 0 0 0 0
x
2
x
3
f
3
0 0 0 0 0 0 1 c
1
c
2
0 0 0 0 0 0
x
3
x
4
f
3
0 0 0 0 0 0 0 0 0 0 0 1 c
1
c
2
0
x
2
4
f
3
0 0 0 0 0 0 0 0 0 0 0 0 1 c
1
c
2
x
2
x
4
f
3
0 0 0 0 0 0 0 1 c
1
c
2
0 0 0 0 0
.
The determinant of this matrix is a univariate polynomial of degree 8 in the vari-
able x
1
given in [28, Box 3-1]. Its roots can be obtained using Matlab’s roots
command. Once these roots have been obtained, the admissible solution is substi-
tuted in the third expression of (13.48) on p. 230 to obtain the value of x
3
∈ R.
+
The obtained value of x
3
∈ R
+
is in turn substituted in the second expression of
(13.48) to obtain the last variable x
2
∈ R.
+
The admissible values of distances are
deduced with the help of prior information.
Approach 2 (B. Sturmfels’ Formulation):
From (13.50) on p. 231, the determinant of the Jacobi matrix is computed as
J = det
∂R
11
∂x
2
∂R
11
∂x
3
∂R
11
∂x
4
∂R
21
∂x
2
∂R
21
∂x
3
∂R
21
∂x
4
∂R
31
∂x
2
∂R
31
∂x
3
∂R
31
∂x
4
, (13.54)
respectively
J = det
2x
2
+ a
1
x
4
0 2a
2
x
4
+ a
1
x
2
2x
2
+ b
1
x
3
2x
3
+ b
1
x
2
2b
2
x
4
0 2x
3
+ c
1
x
4
2c
2
x
4
+ c
1
x
3
, (13.55)
13-2 Geodetic resection 233
which gives a cubic polynomial in x
2
, x
3
, x
4
as
J = 8x
2
x
3
c
2
x
4
+ 4x
2
c
1
x
2
3
+ 4b
1
x
2
2
c
2
x
4
+ 2b
1
x
2
2
c
1
x
3
− 8x
2
b2x
4
x
3
− 4x
2
b2x
2
4
c
1
+
4a
1
x
2
4
x
3
c
2
+ 2a
1
x
4
c
1
x
2
3
+ 2a
1
x
2
4
b
1
x
2
c
2
+ 2a
1
x
4
b
1
x
2
c
1
x
3
−4a
1
x
2
4
b2x
3
−2a
1
x
3
4
b2c
1
+
8x
2
a
2
x
4
x
3
+ 4x
2
a
2
x
2
4
c
1
+ 4a
1
x
2
2
x
3
+ 2a
1
x
2
2
c
1
x
4
+ 4b
1
x
2
3
a
2
x
4
+ 2b
1
x
3
a
2
x
2
4
c
1
+
2b
1
x
2
3
a
1
x
2
,
whose partial derivatives with respect to x
2
, x
3
, x
4
can be written in the form
(5.14) on p. 54. The c oefficients b
ij
and a
ij
are given as in [28]. The computation
of the resultant of the matrix using (5.15) on p. 54 leads to a univariate polynomial
in x
1
of degree eight, e.g., [28, B ox 3-2].
Fischler and Bolles [135, pp. 386-387, Fig. 5] have demonstrated that because
every term in (13.32) is either a constant or of degree 2, for every real positive
solution, there exist a geometrically isomorphic negative solution. Thus there are at
most four positive solutions to (13.32). This is because (13.32) has eight solutions
according to [112, p. 415] who states that for n independent polynomial equations
in n unknowns, there can be no more solution than the product of their respective
degrees. Since each equation of (13.32) is of degree 2 there can only be up to eight
solutions.
Finally, in comparing the polynomial resultants approach to Groebner basis
method, the latter in most cases is slow and there is always a risk of the computer
breaking down during computations. Besides, the Groebner basis approach com-
putes unwanted intermediary elements which occupy more space and thus lead
to storage problems. The overall speed of computation is said to be proportional
to twice exponential the number of variables [286, 287, 288, 290]. This has led
to various studies advocating for the use of the alternate method; the resultant
and specifically multipolynomial resultant approach. Groebner bases can be made
faster by computing the reduced Groebner bases as explained in Chap. 4. For the
special cases used throughout this book, however, this b ound is not so tight since
the size of the solution sets are finite. In such cases, there exist single exponential
bounds.
Polynomial resultants on the other hand involve computing with larger ma-
trices which may require a lot of work. For linear systems and ternary quadrics,
Sturmfels’ approach offers a remedy through the application of the Jacobi determi-
nants. Once the distances have been computed, they are subjected to the ranging
techniques (Chap. 12) to compute positions. Finally, the three-dimensional orien-
tation parameters are computed from (9.10) on p. 118.
13-225 Linear homotopy solution
Example 13.2 (3D resection problem). Let us express the Grunert’s equations
(13.32) in the following form,
x
2
1
− 2f
12
x
1
x
2
+ x
2
2
− d
12
= 0 (13.56)
234 13 Positioning by resection methods
x
2
2
− 2f
23
x
2
x
3
+ x
2
3
− d
23
= 0 (13.57)
x
2
3
− 2f
31
x
1
x
3
+ x
2
1
− d
31
= 0. (13.58)
Numerical data from Awange-Grafarend [41] are used in the following, see Table 13.4.
Table 13.4. Data for 3D resection problem
ϕ
1,2
ϕ
2,3
ϕ
3,1
S
1,2
S
2,3
S
3,1
1.843620 1.768989 2.664537 1560.3302 755.8681 1718.1090
Employing the homotopy solution we need to search 8 paths, because the Bezout
bound in Eq (13.56)-Eq (13.58) is d = 2
3
= 8 (d
1
= 2, d
2
= 2 and d
3
= 2).
Now we have three start equations in our start system generated randomly, using
Eq (6.29)-Eq (6.30),
g
1
= (0.988262 + 0.152767i)
−0.613157 + 0.789961i + x
2
1
(13.59)
g
2
= (0.367759 − 0.929921i)
0.390737 − 0.920503i + x
2
2
(13.60)
g
3
= (−0.530598 + 0.847624i)
0.62502 + 0.780609i + x
2
3
. (13.61)
Table 13.5. shows the solutions of this start system. These values will be the initial
values of the 8 paths of the homotopy function in Eq (13.62).
Table 13.5. Solutions of the start system
i x
1i
x
2i
x
3i
1 −0.898097 + 0.439797i 0.551935 + 0.833887i 0.433001 − 0.901393i
2 −0.898097 + 0.439797i 0.551935 + 0.833887i −0.433001 + 0.901393i
3 −0.898097 + 0.439797i −0.551935 − 0.833887i 0.433001 − 0.901393i
4 −0.898097 + 0.439797i −0.551935 − 0.833887i −0.433001 + 0.901393i
5 0.898097 − 0.439797i 0.551935 + 0.833887i 0.433001 −0.901393i
6 0.898097 − 0.439797i 0.551935 + 0.833887i −0.433001 + 0.901393i
7 0.898097 − 0.439797i −0.551935 − 0.833887i 0.433001 − 0.901393i
8 0.898097 − 0.439797i −0.551935 − 0.833887i −0.433001 + 0.901393i
The homotopy function is the linear combination of the target system, Eq (13.56)-
Eq (13.58) and the start system, Eq (13.59)-Eq (13.61),
H (x
1
, x
2
, x
3
, λ) = (1 − λ)
g
1
(x
1
, x
2
, x
3
)
g
2
(x
1
, x
2
, x
3
)
g
3
(x
1
, x
2
, x
3
)
+ λ
f
1
(x
1
, x
2
, x
3
)
f
2
(x
1
, x
2
, x
3
)
f
3
(x
1
, x
2
, x
3
)
(13.62)
The homotopy paths will be the solution of the following differential equation
system (see Eq (6.15)),
d
dλ
x
1
(λ)
x
2
(λ)
x
3
(λ)
= −H
−1
x
H
λ
(13.63)

13-2 Geodetic resection 235
where the Jacobian
(H
x
)
i,j
= (1 − λ)
∂g
i
∂x
j
i,j
+ λ
∂f
i
∂x
j
i,j
(13.64)
and
(H
λ
)
i
= f
i
(x
1
, x
2
, x
3
) − g
i
(x
1
, x
2
, x
3
) . (13.65)
The end points of these 8 homotopy paths belonging to the eight initial values
in Table 13.5 will give us the eight solutions of the target system Eq (13.56)-
Eq (13.58), provided in Table 13.6.
Table 13.6. End points of the 8 homotopy paths
i x
1i
x
2i
x
3i
1 −22456.5 − 1735.3i 4375.48 + 22037.5i 20757.3 − 8626.43i
2 −1580.11 770.958 −153.711
3 −22456.5 + 1735.3i 4375.48 − 22037.5i 20757.3 + 8626.43i
4 −1324.24 −542.261 −430.529
5 1324.24 542.261 430.529
6 22456.5 − 1735.3i −4375.48 + 22037.5i −20757.3 − 8626.43i
7 1580.11 −770.958 153.711
8 22456.5 + 1735.3i −4375.48 − 22037.5i −20757.3 + 8626.43i
The corresponding solutions for distances in this example should be all positive
real numbers, consequently only the fifth solution is acceptable, see Table 13.7.
Table 13.7. Solution of the 3D resection problem
x
1
= 1324.240
x
2
= 542.261
x
3
= 430.529
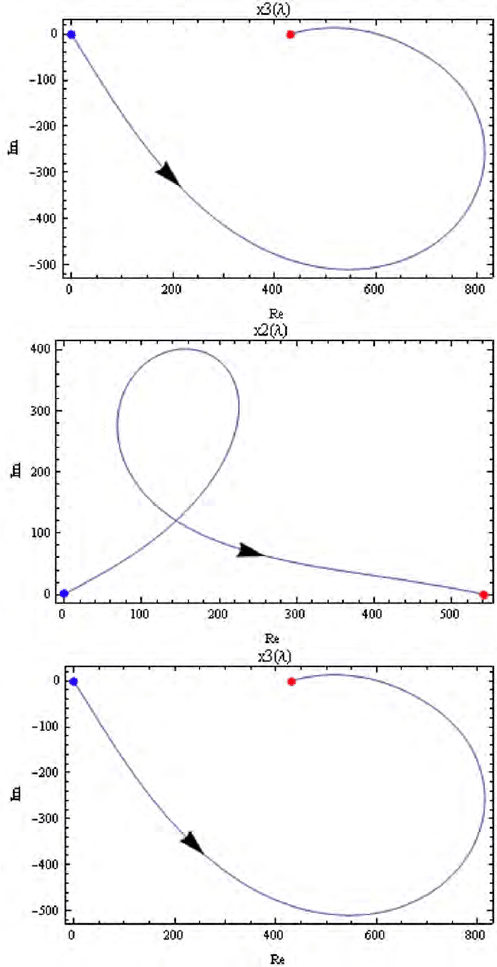
The paths corresponding to this single solution are illustrated in Fig. 13.5.
The computation of the 8 paths takes 0.172 sec with Mathematica. The same
solution was achieved using the reduced Groebner basis, eliminating x
2
and x
3
,
resulted in a univariate polynomial of order 8 for x
1
taking 6.297 sec also in
Mathematica. However, if NSolve employing numerical Groebner basis is used, the
computation time is 0.078 sec. Dixon resultant method improved by [239] and im-
plemented into Mathematica by Nakos and Williams [308] cannot solve the problem
in practicable time (less than 500 sec). However, Dixon method implemented in
the computer algebra system Fermat by [267, 269] can solve the problem in about
0.02 seconds!
236 13 Positioning by resection methods
Figure 13.5. Trajectories of the homotopy path providing positive, real solutions for
the 3D resection problem

13-2 Geodetic resection 237
13-226 Grafarend-Lohse-Schaffrin approach
In this approach, [187] begin by first setting up rigorous projective e quations of
resection problem in three-dimensional Euclidean space. They c lassify the equa-
tions as six dimensional algebraic system of nonlinear equations of cubic type.
In the second part, a three step procedure is adopted for solving the Grunert’s
distance equations. The nonlinear system of distance equations are projected into
linear equations by means of the technique of degenerate quadrics called the stencil
method. The stencil method gives the s olution of Grunert’s equation (13.44) as
x
2
1
= S
2
1
= −
a
00
1 + 2a
12
p + p
2
x
2
2
= S
2
2
= −
b
00
p
2
p
2
+ 2b
23
pq + q
2
x
2
3
= S
2
3
= −
c
00
1 + 2c
31
q + q
2
.
(13.66)
The solution for p and q are as discussed in [187]. Once the distances have been
solved from (13.66), the three orientation parameters and the cartesian coordinates
of the unknown stations are solved from a 6 × 6 system of linear equations. The
linear system of equations are formed using the normalized Hamilton-quaternion
(see e.g., p. 11). For a complete discussion on the approach and a numerical ex-
ample, we refer to papers by [187]. Lohse [276] extends the approach by proposing
an alternative solution of the Grunert’s distance equations.
Example 13.3 (Three-dimensional resection given three known stations). In-order
to position station K1 (see Fig. 10.2 on p. 150) by resection method, horizontal
directions T
i
and vertical directions B
i
are measured to three known stations
Haussmanstr., Eduardpfeiffer, and Liederhalle. The computation is performed in
three steps as follows:
• In the first step, the spatial distances are computed. This involves solving the
Grunert’s distance equations.
• The second step is the computation of the GPS Cartesian coordinates {X, Y, Z}
of the unknown station K1 ∈ E
3
in the global reference frame using the alge-
braic ranging techniques of Chap. 12.
• The three-dimensional orientation parameters are computed in the final step
using the partial Procrustes approach (see Chap. 9).
Using the computed univariate polynomials in [27, Boxes 3-3a and 3-3b] or [28,
Box 3-2], and the observations in Tables 10.1 and 10.3 on p. 152, the distances
S
i
= x
i
∈ R,
+
i = {1, 2, 3} ∈ Z
3
+
between the unknown station K1 ∈ E
3
and the
known stations P
i
∈ E
3
are determined. For control purposes, these distances are
as expressed in Fig. 10.2. The unknown station K1 is located on top of one of the
University’s building at Kepler Strasse 11. Points {P
1
, P
2
, P
3
} of the tetrahedron

238 13 Positioning by resection methods
{P P
1
P
2
P
3
} in Fig. 13.4 correspond to the chosen known GPS stations Haussman-
nstr., Eduardpfeiffer, and Liederhalle. The distance from K1 to Haussmannstr. is
designated S
1
= x
1
∈ R,
+
K1 to Eduardpfeiffer S
2
= x
2
∈ R,
+
while that of K1
to Liederhalle is designated S
3
= x
3
∈ R.
+
The distances between the known sta-
tions {S
12
, S
23
, S
31
} ∈ R
+
are computed from their respective GPS coordinates
as indicated in Solution 13.4. Their corresponding space angles ψ
12,
ψ
23,
ψ
31
are
computed from (13.30) on p. 227.
In-order to control the computations, the Cartesian GPS coordinates of station
K1 are also known. Solution 13.4 gives the unknowns distances {x
1
, x
2
, x
3
} ∈ R
+
computed using Groebner basis. The univariate polynomial in x
3
has eight roots,
four of which are complex and four real. Of the four real roots two are positive
and two are negative. The desired distance x
3
∈ R
+
is thus chosen amongst the
two positive roots with the help of prior information and substituted in [27, g
11
in
Box 3-3b] to give two solutions of x
1
, one of which is positive. Finally the obtained
values of {x
1
, x
3
} ∈ R
+
are substituted in [27, g
5
in Box 3-3b] to obtain the
remaining indeterminate x
2
. Using this procedure, we have in Solution 13.4 that
S
3
= {430.5286, 153.7112}. Since S
3
= x
3
∈ R,
+
from prior information (e.g., Fig.
10.2), we choose S
3
= 430.5286, leading to S
1
= 1324.2381, and S
2
= 542.2608.
These values compare well with their real values depicted in Fig. 10.2 on p. 150.
Solution 13.4 (Computation of distances for test network
Stuttgart Central).
Using the entries of Table 10.1 on p. 152, inter-station distances are computed
by Pythagoras S
ij
=
p
(X
j
− X
i
)
2
+ (Y
j
− Y
i
)
2
+ (Z
j
− Z
i
)
2
, and spatial angles
obtained from (13.30). The values are
S
12
= 1560.3302 m
S
23
= 755.8681 m
S
31
= 1718.1090 m
and
ψ
12
= 1.843620
ψ
23
= 1.768989
ψ
31
= 2.664537
and are substituted in (13.45) on p. 230 to compute the terms a
12
, b
23
, c
31
, a
0
, b
0
, c
0
which are needed to determine the coefficients of the Groebner basis element g
1
in [27, Box 3-3a]. Expressing the univariate polynomial g
1
as A
8
x
8
3
+A
6
x
6
3
+A
4
x
4
3
+
A
2
x
2
3
+ A
0
= 0, the computed coefficients are:
A
0
= 4.833922266706213e + 023
A2 = −2.306847176510587e + 019
A4 = 1.104429253262719e + 014
A6 = −3.083017244255380e + 005
A8 = 4.323368172460818e − 004.
The solutions to the univariate polynomial equation are then obtained using Mat-
lab’s roots command (e.g., 4.42 on p. 46) as
c = [A
8
A
7
A
6
A
5
A
4
A
3
A
2
A
1
A
0
]
x
3
= roots(c),
13-2 Geodetic resection 239
where A
7
, A
5
, A
3
, A
1
are all zero. The obtained values of x
3
are:
x
3
=
−20757.2530734872 + 8626.43262759353i
−20757.2530734872 − 8626.43262759353i
20757.2530734872 + 8626.4326275935i
20757.2530734872 − 8626.4326275935i
430.528578109464
−430.528578109464
153.711222705295
−153.711222705295.
Alternatively, the polynomial resultants techniques can be used to solve the
Grunert’s distance equations. They proceed as follows:
(a) The F. Macaulay formulation discussed in Sect. 5-31 solves for the determinant
of the matrix A leading to a univariate polynomial in x
1
. The solution of the
obtained univariate polynomial equation expressed in [28, Box 3-1] leads to
similar results as those of Groebner basis, i.e.,
det(A) = A
8
x
8
1
+ A
6
x
6
1
+ A
4
x
4
1
+ A
2
x
2
1
+ A
0
A
0
= −4.87154987980622
26
, A
2
= 4.74815547158708
20
A
4
= −113109755605017
A
8
= −0.000432336817247789, A
6
= 435283.472057364
x
1
= −22456.4891074245 + 1735.29702574406i
−22456.4891074245 − 1735.29702574406i
22456.4891074245 + 1735.29702574406i
22456.4891074245 − 1735.29702574406i
1580.10924379877
−1580.10924379877
1324.23808451944
−1324.23808451944
x
3
= 430.528578109536, −2783.30427366986
x
2
= 542.260767703823, −711.800947103387.
(b) The B. Sturmfels formulation discussed in Sect. 5-32 solves the determinant
of a 6 × 6 matrix leading to a univariate polynomial in x
1
. The solution of
the obtained univariate polynomial equation expressed in [28, Box 3-2] gives
identical results as those of Groebner basis, i.e.,
240 13 Positioning by resection methods
det(A) = A
8
x
8
1
+ A
6
x
6
1
+ A
4
x
4
1
+ A
2
x
2
1
+ A
0
A
0
= −1.94861995192249
27
, A
2
= 1.89926218863483
21
A
4
= −452439022420067
A
8
= −0.00172934726897456, A
6
= 1741133.88822977
x
1
= −22456.4891075064 + 1735.29702538544i
−22456.4891075064 − 1735.29702538544i
22456.4891075064 + 1735.29702538544i
22456.4891075064 − 1735.29702538544i
1580.10924379877
−1580.10924379877
1324.23808451944
−1324.23808451944
x
3
= 430.528578109535, −2783.30427366986
x
2
= 542.260767703824, −711.800947103388.
The computed distances from F. Macaulay and B. Sturmfels’ approaches above
tally. The required solutions {x
1
, x
2
, x
3
} obtained from Groebner basis compu-
tation and those of multipolynomial resultants are the same {i.e, 1324.2381 m,
542.2608 m, 430.5286 m} respectively. The computed distances are then used to
determine the position of K1 using ranging techniques discussed in Sect. 12-32.
The unknown orientation elements are computed from (9.10) on p. 118.
13-227 3d-resection to more than three known stations
In the preceding section, only three known stations were required to solve in a
closed form the three-dimension res ection problem for the position and orientation
of the unknown station K1. If superfluous observations are available, due to the
availability of several known stations, as in the case of the test network Stuttgart
Central, closed form three-dimensional resection procedures give way to Gauss-
Jacobi combinatorial approach. We illustrate this by means of Example 13.4.
Example 13.4 (Three-dimensional resection given more than three known stations).
From the test network Stuttgart Central in Fig. 10.2 of Sect. 10-6, the three-
dimensional coordinates {X, Y, Z} of the unknown station K1 are sought. Using
observations in Tables 10.2 and 10.3 on p. 152, the algorithm is applied in four
steps as follows:
Step 1 (combinatorial solution):
From Fig. 10.2, 35 minimal combinatorials are formed using (7.28) on p. 93.
The systems of nonlinear Grunert’s distance equations (13.32) for each of the
35 combinatorials is solved in a closed form to give the distances linking the
unknown station K1 to the 7 known stations. Use is made of either Groebner
basis or polynomial res ultants approaches as already discussed in Sect. 13-22.
Each combinatorial minimal subset results in 3 distances, thus giving rise to a
total of 105 (3 × 35) which are used in the next steps as pseudo-observations.
