Astakhov V. Tribology of Metal Cutting

Подождите немного. Документ загружается.

Tribology of the Tool–Chip and Tool–Workpiece Interfaces 137

(x)

Body 1

Body 2

(a)

(b)

Fig. 3.6. Contact of two bodies: (a) in the undeformed state where they can freely interpenetrate

each other and (b) in the loaded state with no interpenetration permitted.

where

(

3 − ν

)

(

1 + ν

)

in plane stress (3.10)

= 3 −4ν

in plane strain (3.11)

is the Poisson’s ratio, G is the modulus of rigidity (shear modulus), q

(

)

= µ

(

)

where µ

is the friction coefﬁcient.

In general, as two bodies are pressed together, deformation must occur so that the

deformed bodies will conform within the contact. If the unloaded state of the bodies

could freely interpenetrate each other, so that the amount of overlap given by h

(

)

with

maximum c

(Fig. 3.6(a)) within the contact patch, the relative y direction displacements

of surface points υ

− υ

must be equal to the degree of surface overlap, so from

Eqs. (3.8) and (3.9) the required displacement is [71]

∂h

(

)

∂x



(

)

dς

x − ς

−β

(

)

, (3.12)

where

(3.13)

and

(

−1

)

−

(

−1

)

(

)

(

)

(3.14)

138 Tribology of Metal Cutting

Γ =

(3.15)

Thus, A

is the measure of the compliance of the bodies, while β

, sometimes referred

to as the Dundrus’ constant [71], is a measure of the elastic mismatch of the materials.

When the solution to problems under plane strain conditions is needed, then A

and β

become

1 − ν

≡ 2



1 − ν



(3.16)

(

1 − 2ν

)

/2G

−

(

1 − 2ν

)

/2G

(

1 − ν

)

(

1 − ν

)

[(

1 + ν

)(

1 − 2ν

)]

−

[(

1 + ν

)(

1 − 2ν

)]



1 − ν





1 − ν



(3.17)

As known from Ref. [71], the elastic constants of the contacting bodies enter the problem

only through the composite parameters A

and β

. Thus, all pairs of materials yielding

the same values of A

and β

will have the same solution to the contact problem.

In metal cutting, one (the tool) of the two contact bodies is rigid so the elastic constant

of the other body (the chip, when considering the tool ﬂank–workpiece interface) are

adjusted appropriately. As such

1 − ν

≡ 2

1 − ν

(3.18)

1 − 2ν

(

1 − ν

)

(3.19)

As shown by Hills [71], if the relative tangential displacement of any pair of surface

points is h

s−t

(

)

(Fig. 3.6(a)), then this displacement is

∂h

s−t

(

)

∂x



(

)

dς

x − ς

−β

(

)

(3.20)

It is understood that integrations in Eqs. (3.12) and (3.20) are carried out over the entire

contact zone. Thus, to assure equilibrium with external forces P

and Q

, the following

should be kept in mind

=−



(

)

dς (3.21)



(

)

dς, (3.22)

where P

is a positive compressive force.

Tribology of the Tool–Chip and Tool–Workpiece Interfaces 139

p(x)

Elastic limit

(a)

(b)

p(x)

(d)

(c)

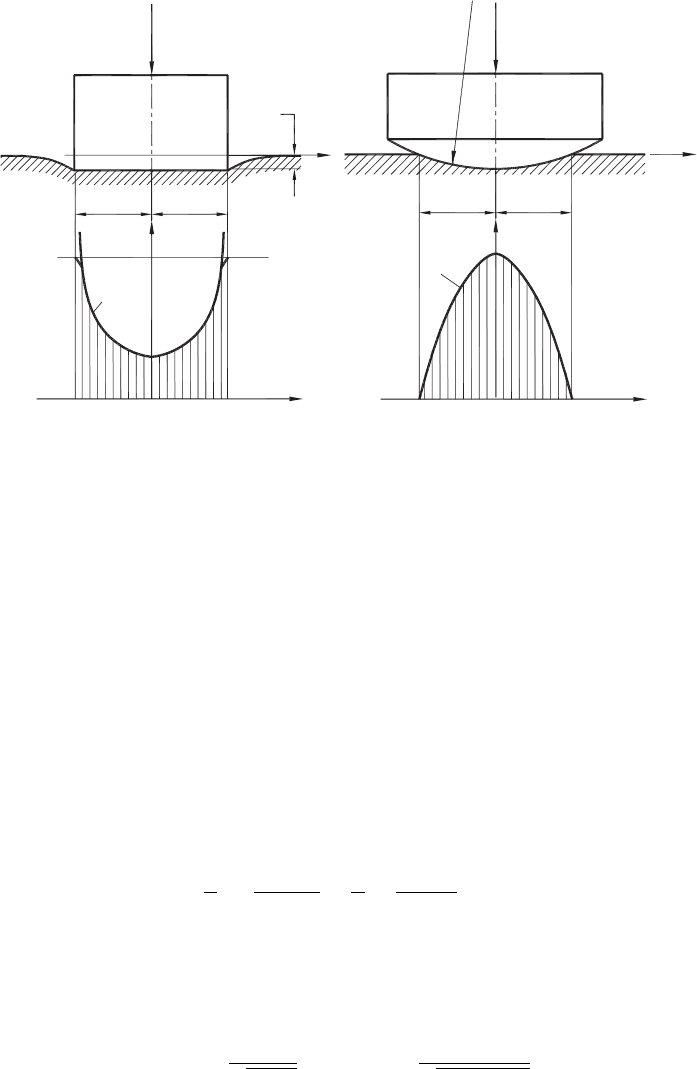
Fig. 3.7. Indentation of a half-plane by: (a) a rigid ﬂat-ended punch and (b) contact stress

distribution, (c) a rigid round-ended punch and (d) contact stress distribution (after Astakhov

and Outeiro [73]).

Poletica [69] was the ﬁrst researcher who attempted to model the tool–chip contact

problem by analyzing the representation of the tool–chip interface as a rigid, ﬂat-ended

axisymmetric cylindrical punch that is pressed into a viscoelastic material, which can be

regarded as semi-inﬁnite, that is, a half-space as shown in Fig. 3.7(a). The contact patch

is of ﬁxed size, independent of the applied load and determined solely by the width of

the indenter.

Since the displacement of the half-plane, h

= constant and no relative motion is allowed,

Eq. (3.12) in normalized coordinates (x = a

s, ς = a

r) gives



−a

(ς)dς

x − ς



−1

(r)dr

s − r

= 0 (3.23)

and its inversion as in Ref. [71] is

p(s) =

√

1 − s

or p(x) =



1 −

(

x/a

)

(3.24)

140 Tribology of Metal Cutting

In Eq. (3.24), C, the constant term included as pressure, is singular at each end of the

contact interval. This constant can be found using Eq. (3.21) as



−a

p(x)dx (3.25)

which gives

(

)



1 −

(

x/a

)

(3.26)

This is known as the Boussinesq solution [71].

Figure 3.7(b) shows the contact pressure distribution, p(x) calculated using Eq. (3.26).

The contact pressure is singular at the edges of the contact. In reality, the contact pressure

is limited by the elastic limit of the body 2 (the chip), as shown in Fig. 3.7(b). Besides,

the edges of the punch (the tool) are not perfectly sharp.

If the sliding of the punch is allowed so that all points within the contact are slipping

in the same direction, then the shear stress acts over this contact. When the friction

coefﬁcient, µ

is constant, this shear stress is deﬁned as

q(x)

= µ

p(x) (3.27)

so that



−a

(ς)dς

x − ς

p(x) = 0 (3.28)

In reality, however, the punch does not have sharp edges as those shown in Fig.3.7(a).

Moreover, its face is not ideally ﬂat. Therefore, the problem of indentation by a general,

convex body should be considered next to approach reality. Figure 3.7(c) shows the rigid

punch having a spherical face of radius r

, which is pressed into a viscoelastic material

that can be regarded as semi-inﬁnite, i.e. a half-space. If the contact is sufﬁciently small

in comparison with the face radius r

, then the problem of contact stress distribution

has a direct solution [72]. The distribution of the contact stress for this case is shown

in Fig. 3.7(d). As seen, when x =±a

, the contact pressure becomes zero, and when

x = 0, this pressure is maximum.

The next step is to start building a model which is closer to the real conditions of the

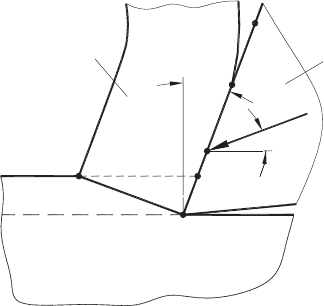
tool–chip interface. Figure 3.8 shows the following essential features of this interface:

• The resultant cutting force R does not intersect the middle point of the tool–chip

contact length OB. Rather, the line of its action is shifted toward the tool point O,

which represents the projection of the cutting edge.

Tribology of the Tool–Chip and Tool–Workpiece Interfaces 141

Chip

Tool

Workpiece

Fig. 3.8. Some characteristic points at the tool–chip interface (after Astakhov and Outeiro [73]).

• The resultant cutting force R is not applied perpendicular to the tool rake face having

the rake angle γ. Rather, it acts at the so-called angle of action, ω

relative to the

direction of tool–workpiece relative motion [2]. As a result, the normal and shear

stresses act over the tool–chip interface.

• As a result of asymmetrical application of the cutting force, the contact pressure

(stress) distribution is no more symmetrical as in the above-considered case.

• There is relative sliding between the tool and the chip so that the friction force

should be considered in the analysis of the contact stresses at the tool–chip

interface.

Considering Fig. 3.8, one can conclude that the tool point O represents the sharp edge

of the punch. According to Figs. 3.7(a) and (b), a normal stress singularity should be the

case in this point. In reality, however, two factors hamper such a singularity. First, the

cutting edge is never perfectly sharp and thus the intersection of the rake and the ﬂank

surfaces of the cutting insert is not a line but rather a surface of ﬁnite radius (this issue will

be discussed later in this chapter). Second, as discussed in Chapter 1, a zone of plastic

deformation in the workpiece forms in the vicinity of this point and a crack originates

from the tool point O in each cycle of chip formation. As known from Ref. [36], plastic

deformation and cracks are means of stress relaxation, so the discussed stress singularity

never occurs in reality. Continue to refer to Fig. 3.8, one can see that the other side of the

tool–chip contact (point B) resembles edge points shown in Fig. 3.7(c), i.e. the contact

pressure becomes zero at this point.

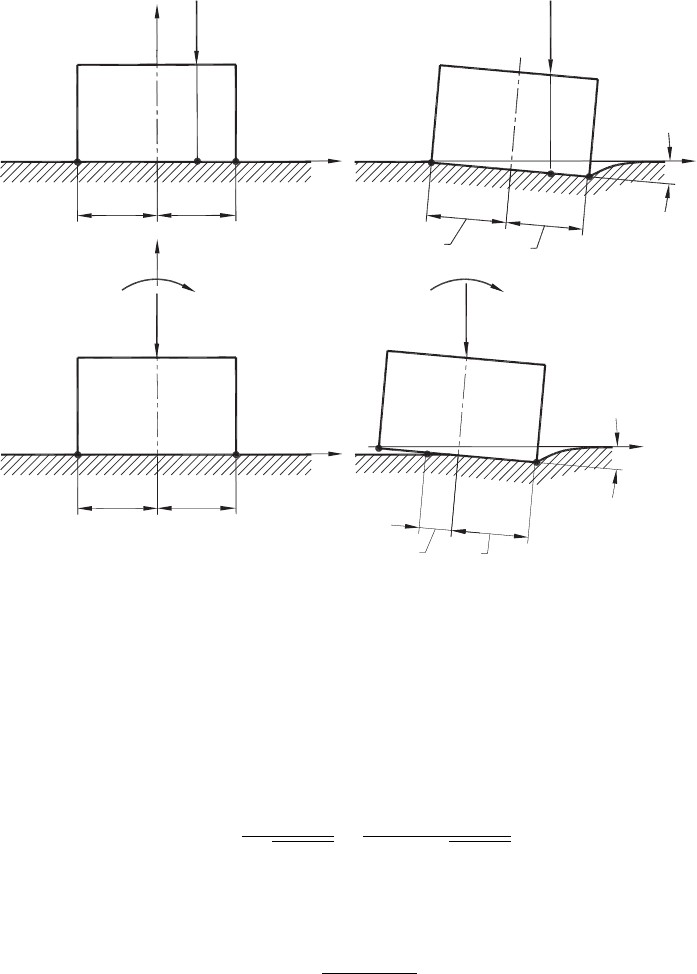
Figure 3.9(a) shows a model of indentation with a ﬂat-face punch and asymmetrical

loading of the punch by force P

applied at point D. As seen, the line of action of force

does not pass through the middle point of the contact length (the xy coordinate origin).

Points O, D and B corresponds to those shown in Fig. 3.8. The asymmetric application

of P

results in asymmetric deformation, as shown in Fig. 3.9(b).

142 Tribology of Metal Cutting

(b)(a)

Fig. 3.9. Indentation of a half-plane by asymmetrically-loaded punch: (a) original model unre-

formed and (b) deformed conﬁgurations; (c) modiﬁed model undeformed and (d) deformed

conﬁgurations (after Astakhov and Outeiro [73]).

The contact stress distribution for the considered case was studied by Muskhelishvili

[72], who obtained the following exact solution

p(x) =



−x

−

(

)



−x

, (3.29)

where c

(

−1

)

2πG

(3.30)

If the sliding of the punch is allowed so that all points within the contact are slipping in

the same direction and when the friction coefﬁcient, µ

is constant, the stress distribution

Tribology of the Tool–Chip and Tool–Workpiece Interfaces 143

becomes

p(x) =

cos πρ

(

)

(

)

−8πG

−4πG

(

−x

)

+ρ

(

−x

)

−ρ

, (3.31)

where

arctan µ

−1

(3.32)

It follows from Eqs. (3.29) and (3.31) that when x =±a

, the contact pressure p(x) =

∞ as in Eq. (3.26). However, the distributions given by Eqs. (3.29) and (3.31) are

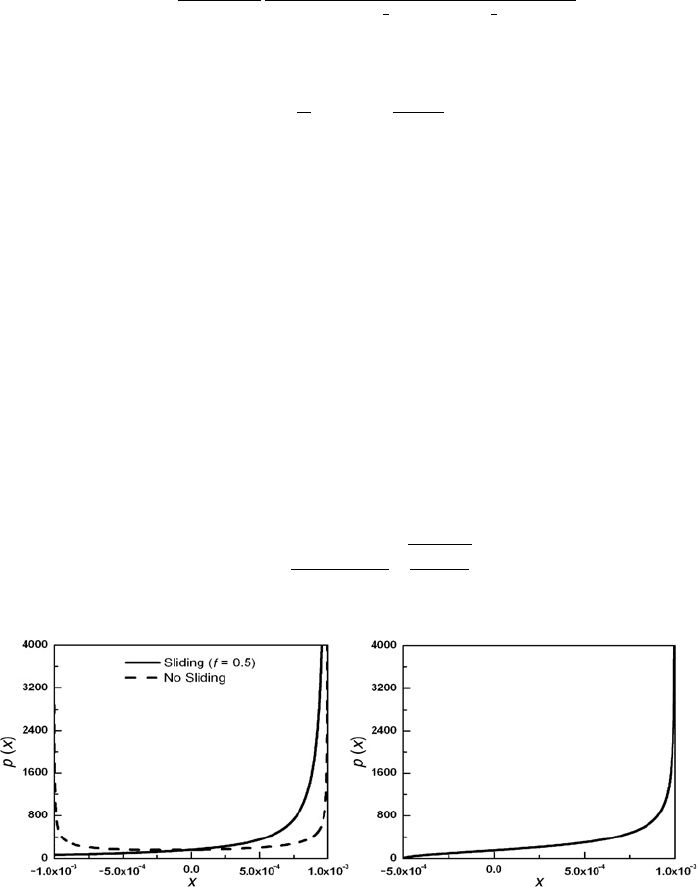
characterized by signiﬁcant asymmetry as seen from Fig. 3.10(a) [73]. This ﬁgure shows

that when the sliding with friction is allowed, the contact stress, p(x), is no more singular

at the punch rear edge, but it tends to zero. Moreover, the accounting for friction (allowing

the sliding at the tool–chip interface) does not affect this distribution signiﬁcantly.

The further development of this model is shown in Fig. 3.9(c) where the force is shifted

to the center of the punch and thus the moment M

is applied to compensate for this shift.

As such, this moment causes the angular punch displacement characterized by angle ζ

and the force P

causes the displacement of the punch in the y direction (the vertical

displacement), as shown in Fig. 3.9(d). As seen, this model is obtained assuming that the

moment M

is great enough such that the point E is not in contact with the workpiece and

the contact length is no more axisymmetrical. Rather, it may be thought of as consisting

of two parts, a

and a

, as shown in Fig. 3.9(d). Studying such a contact problem, Galin

[74] obtained the following analytical solution for the contact stress distribution.

p(x) =

(

)



x + a

−x

(3.33)

(a) (b)

Fig. 3.10. Contact stress distribution (p(x)) produced by applying asymmetrical loading over the

punch: (a) original model sliding with friction is allowed and not allowed, (b) modiﬁed model with

an asymmetrical contact length for the original model. (Conditions: a

= 1×10

−3

m, P

= 0.5N,

= 0.5, E

= 210 GPa, ν

= 0.3) (after Astakhov and Outeiro [73]).

144 Tribology of Metal Cutting

As seen, if x =−a

then p

(

)

= 0 and if x = a

then p

(

)

=∞. Equation (3.33) does

not include M

directly. This moment is accounted for by a

, which is a function of M

Figure 3.10(b) [73] shows the contact stress distribution, p

(

)

, produced in the case of an

asymmetrical contact length. This distribution is similar to the case of full symmetrical

contact with sliding, as shown in Fig. 3.10(a). However, in the case of the asymmetrical

contact length, the stress at point B (Fig. 3.9(d)) is zero.

Although the above-discussed model provides some insight on the contact stress distri-

bution, it is obviously still far from reality because the chip can hardly be modeled by

the half plane representation used in the model. To improve the model, a 3D problem

of contact of a rigid proﬁle with elastic strip should be considered as the next logical

step in model development [69]. Figure 3.11 shows such a model. Using a general form

of solution obtained by Muskhelishvili [72] as applied to the considered case, one can

obtain the following expression for the contact stress distribution

p(x) =

πd



−x

(3.34)

where l

is the contact length, d

is the chip width.

More accurate results can be obtained if friction over the contact length is considered.

As such, the boundary conditions for the stress and displacement should be as follows:

if x<0orx ≥ l

then p(x) = σ

= 0 and τ

= 0. As such

p(x) =

πd

(

1 − 2ρ

)



−x



−ρ

, (3.35)

Chip

Tool

Workpiece

/2l

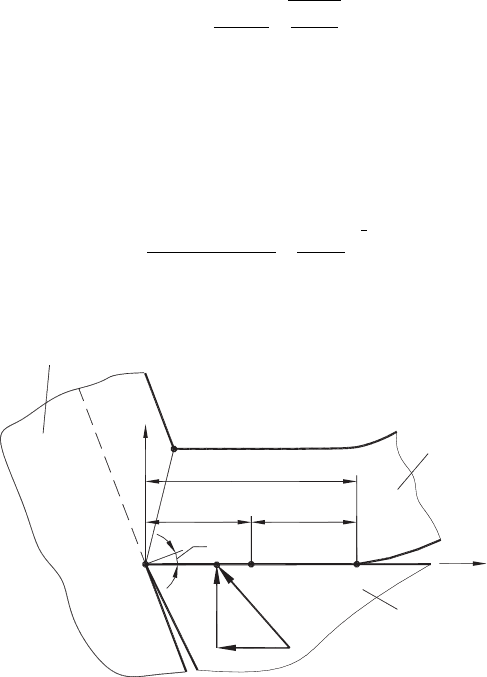
Fig. 3.11. Contact length and its parts (after Astakhov and Outeiro [73]).

Tribology of the Tool–Chip and Tool–Workpiece Interfaces 145

where ρ

calculates using Eq. (2.66). As seen, when µ

= 0, ρ

= 0 and Eq. (3.35)

becomes equivalent to Eq. (3.34).

For convenience, the stress at the tool–chip interface can be represented as the product

of two factors

p(x) = q

(x), (3.36)

where the ﬁrst one,

(3.37)

is the mean contact stress at the tool–chip interface, and the second one is a dimensionless

function

(x) =

2 cos πρ

(

1 − 2ρ

)



−x



−ρ

(3.38)

characterizing the distribution law of the normal pressure over this interface. Equation

(3.38) can be modiﬁed further if a new variable ψ

= x/l

is introduced. As such

(ψ

) =

2 cos πρ

(

1 − 2ρ

)



1 − ψ



−ρ

(3.39)

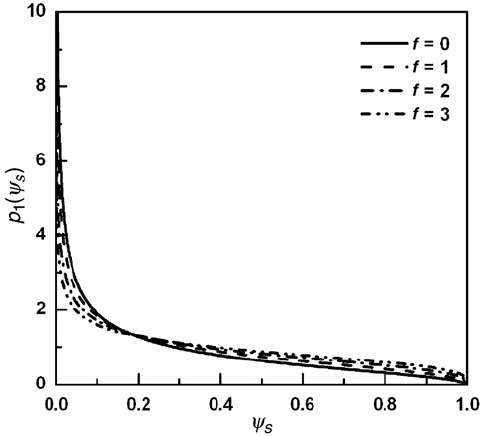
Figure 3.12 shows the distribution of the contact pressure, p

(ψ

) obtained under dif-

ferent friction coefﬁcients [73]. This ﬁgure shows that accounting for friction (allowing

the sliding at the tool–chip interface) does not affect this distribution signiﬁcantly.

One problem about the exact location of the point of application of the penetration force

on the tool rake face remains unsolved. To resolve this problem, an FEM model for the

case shown in Fig. 3.11 was developed using ANSYS commercial FEA software [73].

The developed FEM model utilized the work material properties

(

E, ν

)

, the tool geometry

(

)

and the results obtained from orthogonal cutting tests (forces, N and F, the ﬁnal

angle of the surface of the maximum combined stress (known as the shear angle), and the

tool–chip contact length, l

). The results for the tool–chip contact stress distribution and

equivalent stress distributions in the workpiece and in chip are shown in Figs. 3.13(a) and

(b) for the following conditions: E = 196 GPa, ν

= 0.26, N = 1550 N, F = 1215 N,

γ = 0

◦

, l

= 0.712 mm, l

= 0.284l

. As seen, the maximum stress is found to be at the

region of the cutting edge. This stress decreases exponentially towards the point of chip

separation where this stress is zero.

Interface stress distributions based on the system model. Based upon the system

approach in metal cutting [36,75], this section aims to explain the nature of a signiﬁcant

146 Tribology of Metal Cutting

Fig. 3.12. Contact stress distribution (p

(ψ

)) produced by applying asymmetrical loading over

the punch and considering an asymmetrical contact length, for different friction coefﬁcients

(Conditions: a

= 1 ×10

−3

m, a

= 5 ×10

−4

m, P

= F

= 0.5N,µ

∈

[

0, 3

]

, E

= 210 GPa

and ν

= 0.3) (after Astakhov and Outeiro [73]).

scatter in the reported stress distributions at the tool–chip interface by studying the

dynamics of stress formation and distribution at this interface.

Finite element simulation makes it possible to establish the distributions of the normal

and shear stress at the tool–chip interface, as well as the dynamics of these distributions

within a chip formation cycle. It is instructive to trace the above-mentioned distributions

by applying FEM analysis with incremental loading. The detailed procedure of such

a simulation is developed by Astakhov [36]. Some relevant results obtained are now

considered.

The shear stress distribution at the beginning of each new chip formation cycle is shown

in Fig. 3.14. As seen, this distribution within the tool–chip interface has two distinctive

regions. In the ﬁrst region, the shear stress distributes uniformly and increases with the

applied load. Furthermore, both the length of this region and the stress magnitude do not

change with the rake angle. In contrast, in the second region, the shear stress decreases

at a rate that is a function of the rake angle.

A comparison of the results shown in Fig. 3.14 with the known results shown in Fig. 3.1(b)

shows that there is no contradiction in the reported results. In other words, all the reported

shear stress distributions (curves 1 to 6 in Fig. 3.1(b)) at the tool–chip interface may occur

as being considered at different instants over a chip formation cycle and under different

cutting conditions.