ASM Metals HandBook Vol. 8 - Mechanical Testing and Evaluation

Подождите немного. Документ загружается.

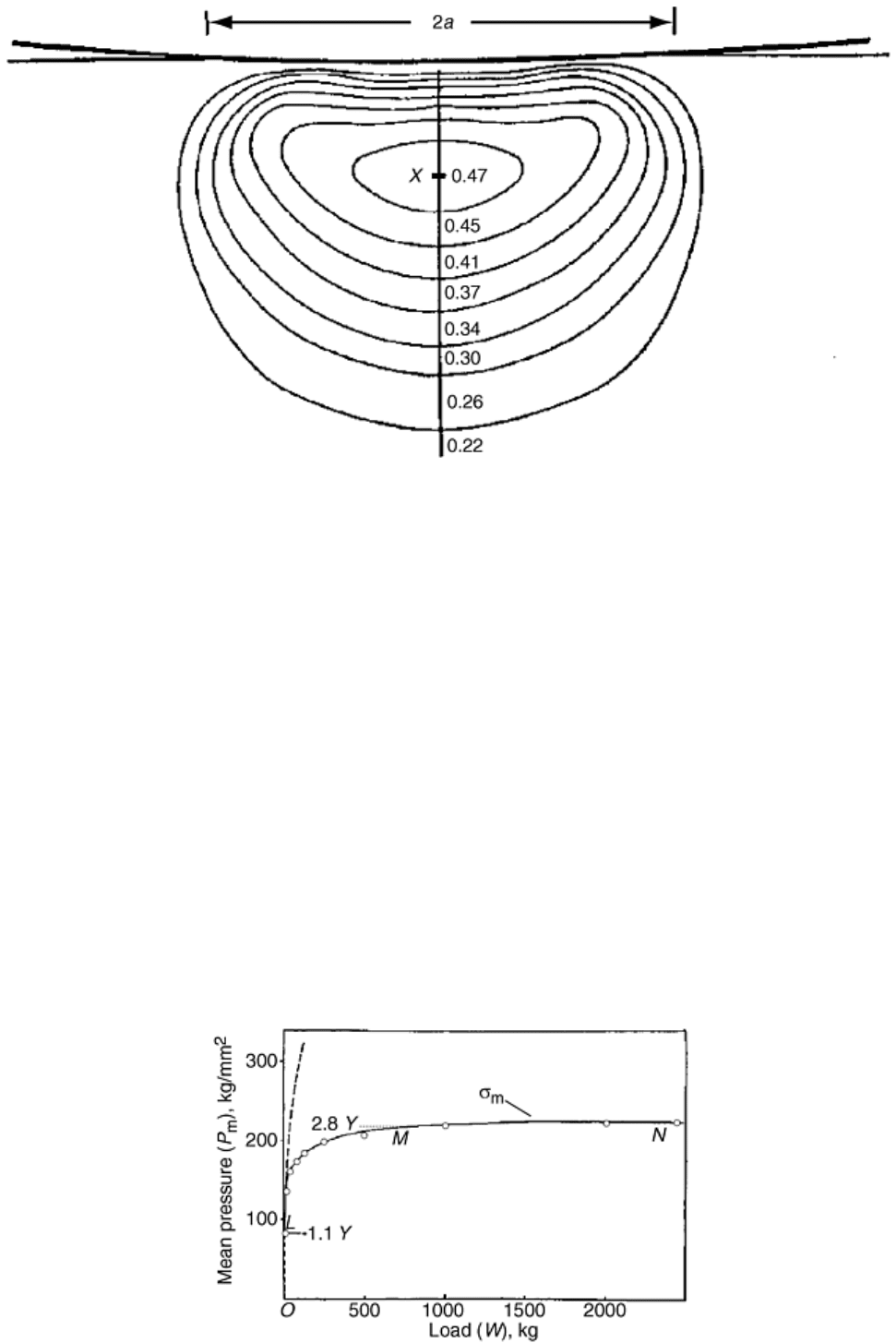
Fig. 4 Elastic defomation of a flat surface on an elastic semi-finite body under a frictionless load, by a

rigid sphere of a large radius, showing the location of maximum shear stress in the bulk material below

the deformed surface. The maximum shear stress occurs at X, 0.5a below the center of the circle of

contact and has a value of about 0.47 P

where P

is the mean pressure. The contours represent lines of

constant shear stress in the deformed material. Source: Ref 6

If the load is reduced or removed before P

reaches the value 1.1Y at X, there will be no permanent deformation

or indentation; that is, there will be a complete elastic recovery. If, however, P

exceeds the value 1.1Y, plastic

deformation begins at X, and the plastic region would grow in size at the expense of the elastic-plastic and

elastic regions underlying the indenter. This process will continue until the mean pressure in the plastic volume

reaches a value ≈3Y. If the load is now increased, the indenter penetrates the metal further, and the plastic zone

would expand until the value of P

in the newly formed plastic volume again equals ≈3Y. When the equilibrium

is reached between the indenter and the material during indentation, and the plastic flow has stopped, the

indenter load is supported by the elastic stresses in the material. If the load is removed, therefore, there will be

an elastic recovery with a corresponding change in shape of the plastically deformed volume and, hence, that of

the indentation.

The spherical indentation process may be visualized through an experimental trace of pressure-load for

indentations formed in work hardened mild steel by a spherical indenter. In Fig. 5, point L represents the onset

of plastic deformation at a mean pressure corresponding to 1.1Y. The interval L-M represents a gradual increase

in the plastic stress, which ultimately reaches a value ≈3Y corresponding to M-N section of the curve when full

plasticity is attained.

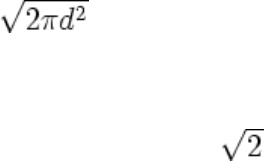
Fig. 5 Experimental pressure-load characteristic of indentations formed in work-hardened mild steel by

a hard spherical indenter. Yield stress of steel, Y = 77 kg/mm

. Ball diameter is 10 mm. The broken line is

the theoretical result for elastic deformation. OL, elastic region; LM, elastic-plastic region; and MN, fully

plastic region. Source: Ref 6

Fully Cold Worked versus Fully Annealed Metals. The above discussion has considered ideal plastic metals,

which, by definition, do not work harden during deformation and show a constant yield stress when the linear

strain is increased as in a tensile or compressive test. Metals that have been sufficiently cold worked would

behave in approximately this manner. However, fully annealed, and, in reality, most metals will have a

tendency to work harden during deformation and will be characterized by a continuously increasing yield stress

with increasing strain. The relation P

= CY (C ≈ 3), which applies to fully cold worked metals, also holds for

fully annealed metals provided Y denotes the yield stress corresponding to the strain produced during testing,

which is higher than the initial yield stress. The value of C has the same approximate value of 3 as for ideal

plastic metals. Also, P

is found to be a function of d/D for fully annealed metals, and therefore, geometrically

similar indentations would give identical hardness values, as for ideal plastic metals. It may be noted here that

the value of C ≈ 3 obtained through slip line analysis as already mentioned has also been recently confirmed

through finite element analysis (Ref 12, 13).

Tabor (Ref 6) showed that the strain, ε, in the plastic region of an indentation is proportional to the ratio d/D

and empirically determined the proportionality constant to be approximately 20 for many metals, thus arriving

at the relation, ε = 20d/D. Combining this equation with the relationship Y = bε

, where b and x are constants for

a given metal and x is the strain hardening coefficient, Tabor has shown that W = c

= c

and so on

for indentations made with indenters of different diameters D

, D

… This is Meyer's law, mentioned earlier

and first derived by Meyer empirically. This relation has been shown to hold fairly well for many materials.

The value of n in the Meyer equation is roughly related to the strain hardening coefficient x by the relation n = x

+ 2.

Conical and Pyramidal Indenters (Ref 6). Shortly after the introduction of Brinell hardness testing, Ludwik (Ref

14) proposed hardness testing using a conical indenter and defined the hardness as the mean pressure over the

surface of the indentation. Thus, for an indent with an included angle of 90°, the Ludwik hardness number is

given by:

HL = 4W /

(Eq 13)

where d is the diameter of the impression. This concept is similar to that of Brinell and therefore has no real

physical significance. The true pressure, P, between the indenter and the indentation is given by the ratio of

load to projected area, that is, 4W/πd

(similar to Meyer's concept for a spherical indenter), which means that

the Ludwik hardness number is 1/ times the mean yield pressure P. Experiments have shown that Ludwik

hardness is practically independent of the load for a given indenter, though it depends on the cone angle. It is

observed that the yield pressure increases as the cone semi-angle decreases, and the effect may be partially

explained as due to friction between the indenter and the indentation (Ref 15).

The diamond pyramidal indenter was first introduced by Smith and Sandland (Ref 16) and was later developed

by Vickers-Armstrong, Ltd. The indenter is in the form of a square pyramid with opposite faces making an

included angle of 136° with each other. The origin of this value of the angle is traced to the Brinell hardness

testing practice. It is customary in Brinell hardness testing to select loads so that the indentation diameter lies

between 0.25D and 0.5D where D is the indenter diameter. Thus, an average of the two diameters, 0.375D, was

chosen for the indentation diameter as shown in Fig. 6, which also shows the origin of the included angle 136°

of the Vickers indenter. The geometry of the indenter is such that projected area of the indentation is 0.927

times the area of the contact surface. Since Vickers hardness, HV, is defined as the load divided by the surface

area of the indentation, the yield pressure, P, is related to the Vickers hardness number by the relation HV =

0.927P.

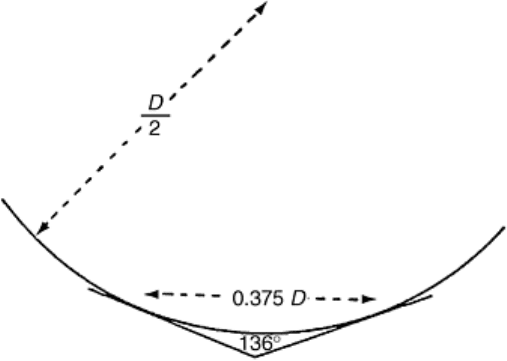
Fig. 6 Relationship between the 136° included angle between the opposite faces of a Vickers indenter and

the spherical Brinell indenter of diameter D

During Vickers hardness tests, the lengths of the two diagonals of the indentation are measured, and their mean

value, d, is calculated. If the indentation is square, the projected area of the indentation is d

/2, so that the yield

pressure is 2W/d

and HV = 0.927 (2W/d

). As in the case of the conical indenter, experiments have shown that

the Vickers hardness number is independent of the size of the indentation, and hence, of the load. It is

interesting to note that the Brinell hardness values, obtained by using a 10 mm steel ball loaded to give an

indentation diameter equal to 0.375D, have been shown to closely match the Vickers hardness numbers (Ref

17), thus giving some justification to the selection of 136° as the included angle.

The Knoop diamond indenter is a variation of the Vickers indenter. It is a pyramid in which the included angles

are 172° 30′ and 130°, and the indentation has the shape of a parallelogram with the longer diagonal about

seven times as long as the shorter diagonal. The Knoop hardness is defined as the load, W, divided by the

projected area A of the indentation. Thus HK = W/A, which gives the yield pressure. The hardness values

obtained by the Knoop method are, as would be expected, nearly independent of the load and are almost

identical with HV numbers.

The elastic and plastic deformation processes that occur in the case of conical and pyramidal indenters are

similar to those described for a spherical indenter.

Again, as in the case of a flat punch already described, slip line analysis has been done (Ref 18) for the plastic

deformation under a two-dimensional conical and pyramidal indenter in the form of a wedge. The slip line

pattern in Fig. 7 shows that the analysis allows for metal flow past the indenter surface to form a ridge. The

pressure normal to the indenter surface is given by (Ref 6):

P = 2k(1 + θ)

(Eq 14)

where θ is the angle as shown in Fig. 6, and is related to α, the semi-angle of the wedge, by the equation:

Cos(2 α - θ) = cosθ/(1 + sin θ)

(Eq 15)

Since 2k = 1.15Y for Huber-Mises criterion:

P = 1.15Y(1 + θ)

(Eq 16)

As seen from Fig. 7, when the semi-angle α = 90°, θ = 90°. The wedge forms flat punch, as discussed. Equation

15 becomes:

P = 1.15Y(1 + ½π)

(Eq 17a)

P = 2.96Y

(Eq 17b)

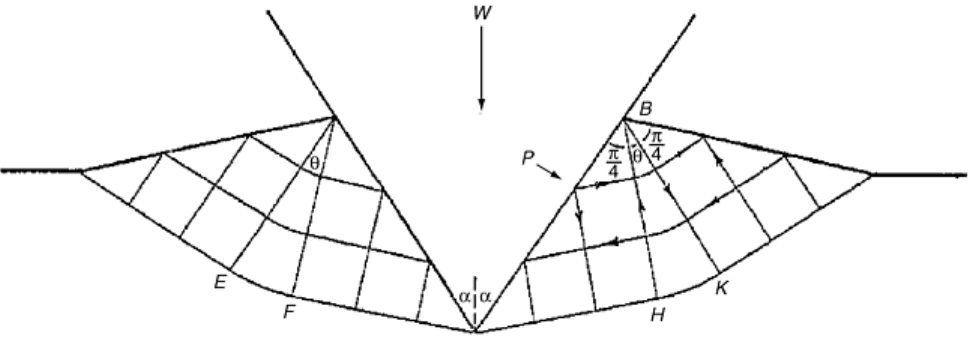
Fig. 7 Slip-line pattern for a two-dimensional wedge penetrating an ideally plastic material (Ref 18). The

pressure across the face of the indenter is uniform and has the value P = 2k(1 + θ), where θ is the angle

HBK in radians. This analysis allows for the displacement of the deformed material as can be seen in the

figure. Source: Ref 6

Equation 17a 17b is the same as Eq 12 derived for a flat punch and shows the yield pressure is again about three

times the yield stress. The two-dimensional analysis and the expression for yield pressure (P = CY) for a wedge

are expected to apply to the case of solid pyramidal and conical indenters just as the flat punch analysis was

found to hold fairly well for a flat circular punch. In fact, it has been shown experimentally that it is true.

However, the value of C for these solid indenters is found in practice to be slightly higher than for a spherical

indenter (3.2 versus 3.0), and this is considered to be probably due to the higher friction between the indenter

and the material.

The pyramidal and conical indenters may be considered to have a spherical indentation point with an extremely

small radius. The plastic deformation therefore starts immediately after the indenter comes in contact with the

material surface, even at very small loads. As the load is increased, the indentation increases in size and depth,

but its shape and the flow pattern remain unchanged whatever its depth. This implies that the indentations

produced by these indenters are geometrically similar for all indentation loads, and hence, the hardness values

measured by these indenters are, for all practical purposes, independent of the indentation load (compare this

with the case of the Brinell test where the requirement is that the d/D ratio should be constant to obtain identical

hardness values).

The preceding discussion is true for the commonly used microhardness and macrohardness tests with

indentations above a certain size where the hardness is independent of their depth. However, recent

investigations have shown that for indentations of extremely small depths (50 nm), the hardness can vary

inversely with depth due to the probable influence of several surface factors such as dislocation image forces,

contamination layers, and electric fields (Ref 19).

Rockwell Hardness Test with a Conical Indenter. In the Rockwell test, a load of 10 kg is first applied to the

material surface, and the depth of penetration is considered as zero for further depth measurements. A load of

90 or 140 kg is then applied and removed, leaving the minor load in place, and the additional depth of

penetration is measured directly on a dial gage, which gives the hardness value that may be correlated with

Vickers or Brinell values. In the Rockwell test, a spherical indenter is used for softer materials (Rockwell B

scale), and a conical indenter is used for hard materials (Rockwell C scale). Other scales of Rockwell test are

omitted from this discussion but are described in the article “Indentation Hardness Testing of Metals and

Alloys” in this Section.

Rockwell testing has two important advantages as compared to other tests previously discussed:

• Application and retention of the minor load during the test prepares the surface upon which the

incremental penetration depth due to the major load is measured.

• The hardness value is read directly on the dial gage without the necessity for measuring the indentation

dimensions, as in other hardness testing methods. This expedites the testing process—an important

advantage in manufacturing and quality control.

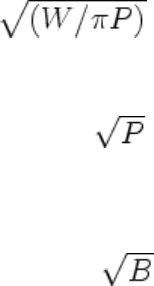
However, there may be appreciable elastic recovery of the material when the major load is removed, and the

recovered indentation depth will be less than the depth before removing the load. The hardness value deduced

from the depth of recovered indentation may, therefore, be in error. This error may not be serious if the

instrument is calibrated for materials having approximately the same elastic modulus, a requirement that is

generally satisfied in industry where the most common materials used in manufacturing are ferrous and have

approximately the same elastic modulus.

If the above effect is neglected and the plastic deformation is large compared to the elastic recovery, then it is

relatively simple to obtain a relationship between the hardness values obtained from depth measurements and

those from diameter measurements of the spherical indentation. Thus, assuming that the penetration depth, t, is

small as compared to the ball diameter, D, one can obtain from simple geometry considerations that t = d

/4D

where d is the diameter of the indentation. Since the mean pressure P across the indentation, which is

equivalent to the Meyer hardness, is given by P = 4W/πd

t = (W/P)(1/πD)

(Eq 18)

Thus, if the load is kept constant as in a Rockwell test, Eq 18 shows depth of penetration t is inversely

proportional to P; that is, the depth of penetration increases with decreasing hardness. This fact is reflected in

the dial gage readings, which do not give the actual depth of penetration but, rather, give a quantity, R, given by

100 scale divisions minus the depth penetrated. Thus:

R = constant - t

R = C

- C

/ P

(Eq 19)

where C

and C

are constants.

This type of relation is approximately obeyed if a spherical indenter is employed. However, a different relation

is obtained if a conical indenter is used. Thus if α is the semi-angle of the cone and the depth of penetration is t

= a cotα where 2a is the indentation diameter, then:

t = cotα

(Eq 20)

where P, the mean pressure, is again given by P = W/πa

. Since t is inversely proportional to P for a given value

of α, the Rockwell number may be expressed by the relationship:

R = C

- C

(Eq 21)

where C

and C

are constants. If Rockwell hardness values R

, obtained using a spherically tipped conical

indenter, are plotted against Brinell hardness numbers, B, it is found that the curve can be approximately

represented by the relationship:

= C

- C

(Eq 22)

where C

and C

are constants.

Equation 22 is similar to Eq 21 with P replaced by B. Since it is reasonable to assume Meyer hardness P is not

widely different from B, it may be concluded that the theoretical relation between R

and B (Eq 21) is

substantiated by the empirical observations (Eq 22), and this provides a degree of validity to the concept of

measurement of hardness from depth measurements.

Summary. The indentation hardness values are essentially a measure of the elastic limit or yield stress of the

material being tested. For most types of indenters in use, the yield pressure under conditions of appreciable

plastic flow is approximately three times the yield stress of the material. The elastic recovery of the indentation

when the load and the indenter are removed seems to affect mostly the depth of the indentation rather than the

projected area of the indentation. Consequently the yield pressure or the hardness as measured from the

indentation dimensions are nearly the same as would be obtained if measurements were made before the load

and the indenter were removed.

The yield pressure is mostly dependent on the plastic properties of the material and only to a secondary extent

on the elastic properties. If the hardness measurements are made based on the depth measurements, then the

elastic recovery may affect the calculated yield pressure, which may be in error when compared with the actual

values that may be obtained during indentation. However, this error may be small when the instrument is

calibrated for materials with similar elastic moduli.

With conical and pyramidal indenters, the indentations are geometrically similar (whatever the indentation

size), and, therefore, the mean pressure to produce the plastic flow is almost independent of the indentation

size. Consequently the hardness value is fairly constant over a wide range of loads. This means it is not

necessary in practice to specify the load.

With spherical indenters, the shape of the indentation varies with its size so that the amount of work hardening,

the elastic limit, and, as a result, the yield pressure in general increase with the size of the indentation and hence

with the load. It is therefore necessary in Brinell hardness measurements to specify the load and the diameter of

the indenter. With spherical indenters the ratio W/D

must be maintained constant to produce geometrically

similar indentations and nearly identical hardness numbers.

In Brinell testing, the increase in the yield pressure with the size of indentation provides useful information

about the yield stress of the material and about the way in which the yield stress increases with the amount of

deformation. In fact, the hardness measurements made using a spherical indenter can be used in conjunction

with the Meyer analysis and Meyer's index, n, to determine the work hardening coefficient, x, using the

relationship n = x + 2.

References cited in this section

6. D. Tabor, The Hardness of Metals, Clarendon Press, Oxford, 1951

7. E. Meyer, Zeits. D. Vereines Deutsch. Ingenieure, Vol 52, 1908, p 645

8. L. Prandtl, Nachr. d. Gesellschaft d. Wissensch, zu Göttingen, Math.-Phys.Klasse, 1920, p 74

9. R. Hill, The Mathematical Theory of Plasticity, Oxford, 1950, p 254

10. S. Timoshenko, Theory of Elasticity, McGraw-Hill, 1934

11. R.M. Davies, Proc. R. Soc. (London) A, Vol 197, 1949, p 416

12. Y.-T. Cheng and C.-M. Cheng, Philos. Mag. Lett., Vol 77 (No. 1), 1998, p 39–47

13. A. Bolshakov and G.M. Pharr, J. Mater. Res., Vol 13 (No. 4), April 1998, p 1049–1058

14. P. Ludwik, Die Kegelprobe, J. Springer (Berlin), 1908

15. G.A. Hankins, Proc. Inst. Mech. Eng. D, 1925

16. R. Smith and G. Sandland, Proc. Inst. Mech. Eng., Vol 1, 1922, p 623

17. S.R. Williams, Hardness and Hardness Measurements, American Society for Metals, 1942

18. R. Hill, E.H. Lee, and S.J. Tupper, Proc. R. Soc. (London) A, 1947, Vol 188, p 273

19. W.C. Oliver, R. Hutchings, and J.B. Pethica, STP 889, ASTM, 1995, p 90–108

Introduction to Hardness Testing

Gopal Revankar, Deere & Company

Classification of Hardness Tests

The hardness tests may be classified using various criteria, including type of measurement, magnitude of

indentation load, and nature of the test (i.e., static, dynamic, or scratch).

Type of Measurement. Hardness tests may be classified into two types: one, involving measurement of

dimensions of the indentation (Brinell, Vickers, Knoop) and the other, measuring the depth of indentation

(Rockwell, nanoindentation). They may also be classified as the traditional tests, which measure one contact

area or penetration depth at a prescribed load (Brinell, Vickers, Knoop, Rockwell), and the recent instrumented-

indentation tests, which allow for a continuous measurement of load and displacement.

Magnitude of Indentation Load. Hardness tests may be classified based on the magnitudes of indentation loads.

There are, thus, macrohardness, microhardness, and the relatively new nanohardness tests. For macrohardness

tests, indentation loads are 1 kgf or greater:Vickers testing may use loads from 1 to 120 kgf. Rockwell test

loads vary from 15 to 150 kgf, depending on the type of indenter and the Rockwell scale of measurement.

Brinell tests involve 500 and 3000 kgf loads though intermediate loads. Loads as low as 6.25 kgf are

occasionally used.

The microhardness tests (Vickers and Knoop) use smaller loads ranging from 1 gf to 1 kgf, the most common

being 100 to 500 gf and suited for material layers that are thicker than about 3 mm. The nanoindentation test,

also called the instrumented indentation test, depends on the simultaneous measurement of the load and depth

of indentation produced by loads that may be as small as 0.1mN, with depth measurements in the 20 nm range.

Static, Dynamic, or Scratch Types. All of the above mentioned tests are of the static type. In the dynamic tests,

the indenter, usually spherical or conical, is allowed to bounce off the surface of the material to be tested, and

the rebound height of the indenter is used as a measure of hardness. The scleroscope is the most popular test of

this type. In the scratch test, a material of known hardness is used to scratch the surface of material of unknown

hardness to determine if the latter is more or less hard than the reference material.

Eddy current hardness testing, which does not fall into any of the above categories, is a noncontact method and

does not use an indenter. The method depends on the measurement of eddy current permeability of the material

surface layer, which is determined by its microstructure and hence hardness.

These and various other test methods are discussed in greater detail in the subsequent articles of this Section.

Introduction to Hardness Testing

Gopal Revankar, Deere & Company

Acknowledgments

Substantial portions of this brief review are adaptations from the classic work of Tabor on hardness (Ref 6).

The author is indebted to the continued usefulness of that book.

Reference cited in this section

6. D. Tabor, The Hardness of Metals, Clarendon Press, Oxford, 1951

Introduction to Hardness Testing

Gopal Revankar, Deere & Company

References

1. R.W. Rice, The Compressive Strength of Ceramics in Materials Science Research, Vol 5, Ceramics in

Severe Environments, W.W. Kriegel and H. Palmour III, Ed., Plenum, 1971, p 195–229

2. J.A. Brinell, II Cong. Int. Méthodes d' Essai (Paris), 1900

3. M.O. Lai and K.B. Lim, J. of Mater. Sci., Vol 26 (1991), p 2031–2036

4. S.C. Chang, M.T. Jahn, C.M. Wan, J.Y.M. Wan, and T.K. Hsu, J. Mater. Sci., Vol 11, 1976, p 623

5. W. Kohlhöfer and R.K. Penny, Int. J. Pressure Vessels Piping, Vol 61, 1995, p 65–75

6. D. Tabor, The Hardness of Metals, Clarendon Press, Oxford, 1951

7. E. Meyer, Zeits. D. Vereines Deutsch. Ingenieure, Vol 52, 1908, p 645

8. L. Prandtl, Nachr. d. Gesellschaft d. Wissensch, zu Göttingen, Math.-Phys.Klasse, 1920, p 74

9. R. Hill, The Mathematical Theory of Plasticity, Oxford, 1950, p 254

10. S. Timoshenko, Theory of Elasticity, McGraw-Hill, 1934

11. R.M. Davies, Proc. R. Soc. (London) A, Vol 197, 1949, p 416

12. Y.-T. Cheng and C.-M. Cheng, Philos. Mag. Lett., Vol 77 (No. 1), 1998, p 39–47

13. A. Bolshakov and G.M. Pharr, J. Mater. Res., Vol 13 (No. 4), April 1998, p 1049–1058

14. P. Ludwik, Die Kegelprobe, J. Springer (Berlin), 1908

15. G.A. Hankins, Proc. Inst. Mech. Eng. D, 1925

16. R. Smith and G. Sandland, Proc. Inst. Mech. Eng., Vol 1, 1922, p 623

17. S.R. Williams, Hardness and Hardness Measurements, American Society for Metals, 1942

18. R. Hill, E.H. Lee, and S.J. Tupper, Proc. R. Soc. (London) A, 1947, Vol 188, p 273

19. W.C. Oliver, R. Hutchings, and J.B. Pethica, STP 889, ASTM, 1995, p 90–108

Macroindentation Hardness Testing

Edward L. Tobolski, Wilson Instruments Division, Instron Corporation; Andrew Fee, Consultant

Introduction

ALMOST ALL indentation hardness testing is done with Brinell, Rockwell, Vickers, and Knoop indenters.

These modern methods of indentation testing began with the Brinell test, which was developed around 1900

when the manufacturing of ball bearings prompted J.A. Brinell in Sweden to use them as indenters. The Brinell

test was quickly adopted as an industrial test method soon after its introduction, but several limitations also

became apparent. Basic limitations included test duration, the large size of the impressions from the indent, and

the fact that high-hardness steels could not be tested with the Brinell method of the early 1900s.

The limitations of the indentation test developed by Brinell prompted the development of other

macroindentation hardness tests, such as the Vickers test introduced by R. Smith and G. Sandland in 1925, and

the Rockwell test invented by Stanley P. Rockwell in 1919. The Vickers hardness test follows the same

principle of the Brinell test—that is, an indenter of definite shape is pressed into the material to be tested, the

load removed, the diagonals of the resulting indentation measured, and the hardness number calculated by

dividing the load by the surface area of indentation. The principal difference is that the Vickers test uses a

pyramid-shaped diamond indenter that allows testing of harder materials, such as high-strength steels.

The Rockwell hardness test differs from Brinell hardness testing in that the hardness is determined by the depth

of indentation made by a constant load impressed upon an indenter. Rockwell hardness testing is the most

widely used method for determining hardness, primarily because the Rockwell test is fast, simple to perform,

and does not require highly skilled operators. By use of different loads (force) and indenters, Rockwell hardness

testing can determine the hardness of most metals and alloys, ranging from the softest bearing materials to the

hardest steels.

This article describes the principal methods for macroindentation hardness testings by the Brinell, Vickers, and

Rockwell methods. Microindentation hardness tests with the Knoop and Vickers indenters are described further

in the next article “Microindentation Hardness Testing.” An overall discussion on the applications and selection

of these test methods is provided in the article “Selection and Industrial Applications of Hardness Tests” in this

Volume.

Macroindentation Hardness Testing

Edward L. Tobolski, Wilson Instruments Division, Instron Corporation; Andrew Fee, Consultant

Rockwell Hardness Testing

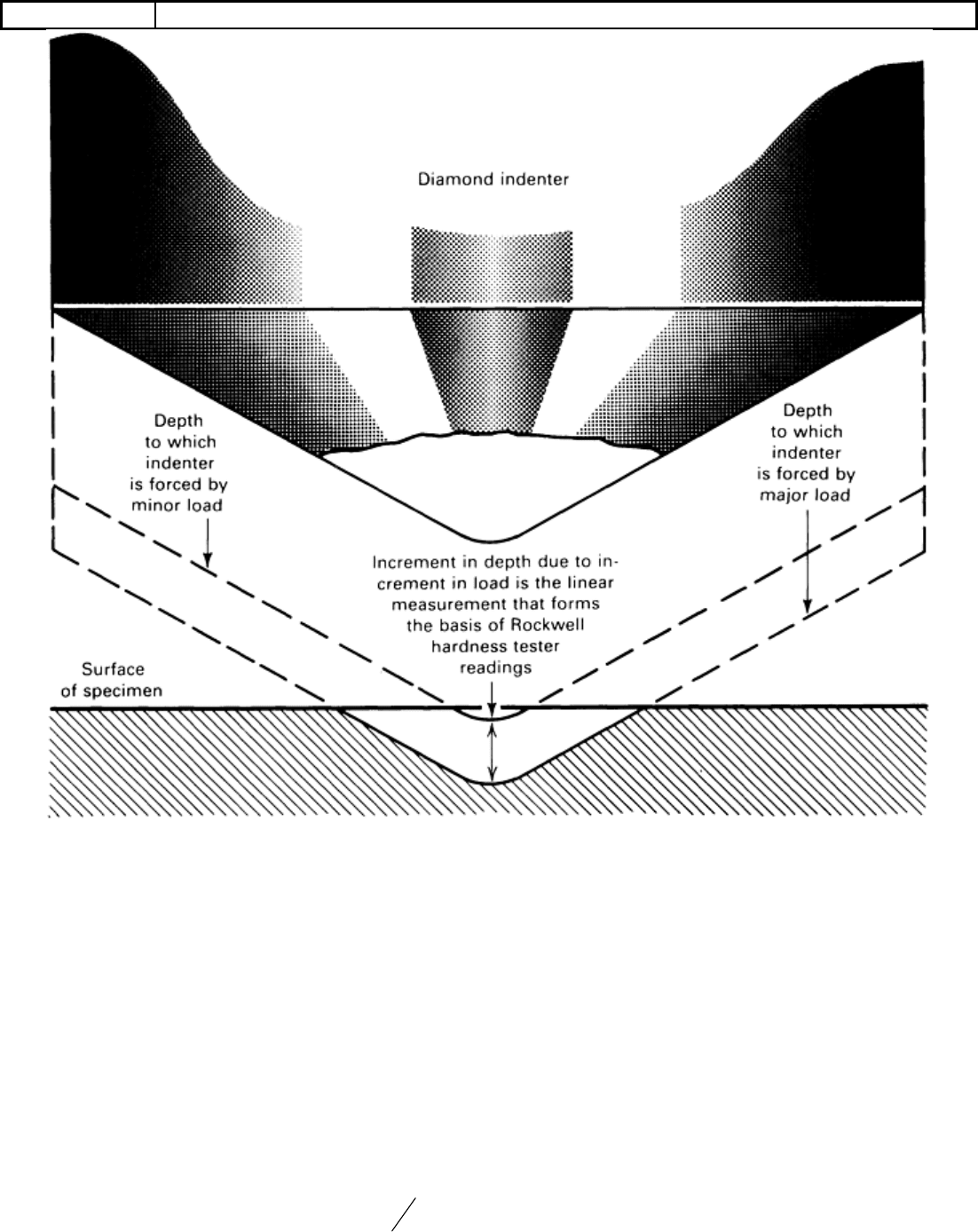
The Rockwell hardness test is defined in ASTM E 18 and several other standards (Table 1). Rockwell hardness

testing differs from Brinell testing in that the Rockwell hardness number is based on the difference of indenter

depth from two load applications (Fig. 1). Initially a minor load is applied, and a zero datum is established. A

major load is then applied for a specified period of time, causing an additional penetration depth beyond the

zero datum point previously established by the minor load. After the specified dwell time for the major load, it

is removed while still keeping the minor load applied. The resulting Rockwell number represents the difference

in depth from the zero datum position as a result of the application of the major load. The entire procedure

requires only 5 to 10 s.

Table 1 Selected Rockwell hardness test standards for metals and hardmetals

Standard No. Title

ASTM B 294 Standard Test Method for Hardness Testing of Cemented Carbides

ASTM E 18 Test Methods for Hardness and Rockwell Superficial Hardness of Metallic Materials

ASTM E 1842 Test Method for Macro-Rockwell Hardness Testing of Metallic Materials

BS 5600-4.5 Powder Metallurgical Materials and Products—Methods of Testing and Chemical Analysis of

Hardmetals—Rockwell Hardness Test (Scale A)

BS EN ISO

6508-1

Metallic Materials—Rockwell Hardness Test—Part 1: Test Method (Scales A, B, C, D, E, F,

G, H, K, N, T)

BS EN ISO

6508-2

Metallic Materials—Rockwell Hardness Test—Part 2: Verification and Calibration of Testing

Machines (Scales A, B, C, D, E, F, G, H, K, N, T)

BS EN ISO

6508-3

Metallic Materials—Rockwell Hardness Test—Part 3: Calibration of Reference Blocks

(Scales A, B, C, D, E, F, G, H, K, N, T)

ISO 3738-1 Hardmetals—Rockwell Hardness Test (Scale A)—Part 1: Test Method

ISO 3738-2 Hardmetals—Rockwell Hardness Test (Scale A)—Part 2: Preparation and Calibration of

Standard Test Blocks

JIS B 7726 Rockwell Hardness Test—Verification of Testing Machines

JIS B 7730 Rockwell Hardness Test—Calibration of Reference Blocks

JIS Z 2245 Method of Rockwell and Rockwell Superficial Hardness Test

Fig. 1 Principle of the Rockwell test. Although a diamond indenter is illustrated, the same principle

applies for steel ball indenters and other loads.

Use of a minor load greatly increases the accuracy of this type of test, because it eliminates the effect of

backlash in the measuring system and causes the indenter to break through slight surface roughness. The basic

principle involving minor and major loads is shown in Fig. 1. Although the principle is illustrated with a

diamond indenter, the same principle applies for hardened steel ball indenters and other loads.

Test Types and Indenters

There are two types of Rockwell tests: Rockwell and superficial Rockwell. In Rockwell testing, the minor load

is 10 kgf, and the major load is 60, 100, or 150 kgf. In superficial Rockwell testing, the minor load is 3 kgf, and

major loads are 15, 30, or 45 kgf. In both tests, the indenter may be either a diamond cone or a hardened ball

depending principally on the characteristics of the material being tested.

Hardened ball indenters with diameters of

, ⅛ , ¼ and, ½in. (1.588, 3.175, 6.35, and 12.7 mm) are used

for testing softer materials such as fully annealed steels, softer grades of cast irons, and a wide variety of

nonferrous metals. Hardened steel balls have traditionally been used for Rockwell testing. However, a

changeover to tungsten carbide is in process. All future testing will be done with carbide balls. This will

improve the durability of the balls significantly, but a slight change in hardness results may occur.