ASM Metals HandBook Vol. 17 - Nondestructive Evaluation and Quality Control
Подождите немного. Документ загружается.

3.0 1,000
0.001
4.0 10,000 0.0001
If the light transmitted through the film is half of the incident light (transmittance = 0.5), the density is only 0.3, and for a
density of 1.0, only one-tenth of the incident light intensity is transmitted. The fact that only of the incident light is
transmitted at a density of 2.0 is the reason that it is necessary to use high-intensity illuminators for viewing industrial
radiographs at densities exceeding 2.0.
Exposure is the intensity of radiation multiplied by the time during which it acts, that is, the amount of energy that
reaches a particular area of the film and that is responsible for producing a particular density on the developed film.
Exposure can be specified either in absolute units (such as ergs per square centimeter or roentgens) or in relative units
(where one particular exposure is used as a reference and all others are specified in terms of that reference). Unless
equipment and time are available for making the precise radiation measurements that are required for defining exposure in
absolute units, relative exposure is much more convenient than absolute and is equally as useful.
In discussing film properties, only absolute exposure or relative exposure as defined above is appropriate. Relative
exposure is used in the present discussion.
Characteristic Curves. The relation between the exposure applied to a given type of radiographic film and the
resulting density is expressed in a curve known as the characteristic curve of that particular type of film. Other names for
this curve are the H and D curve, D log E curve, or sensitometric curve. Such curves are determined by applying a series
of known exposures to the film and, after processing the film according to a standard procedure, reading the resulting
densities. The curve is generated by plotting density against the logarithm of relative exposure. Figure 36(a) shows the
characteristic curves of three commercial films exposed to x-radiation between lead screens.

Fig. 36 Characteristic curves for x-
ray film that determine type of film and film gradient, speed, and density.
(a) Typical curves for three industrial x-ray films exposed to x-radiation between lead screens. (b) Evaluat
ion of
gradients at two points on the curve for film A in (a). (c) Density differences ( D
) corresponding to a 20%
difference in relative exposure ( log E
= 0.08) determined for the two values of gradients evaluated in (b).
(d) Average gradients for film A determined over two density ranges
Relative exposure is used partly because there are no convenient units suitable to all kilovoltages and scattering
conditions and partly because it is easy to determine the logarithm of relative exposure. Using the logarithm of relative
exposure instead of only relative exposure has several other advantages; for example, the otherwise long scale is
compressed, and ratios of intensities or exposures (which are determined by simply subtracting logarithms) are usually
more significant in radiography than actual exposures or intensities.
Characteristic curves are very useful in determining the speed and gradient of the film as well as indicating the type of
film. For example, in Fig. 36(a), characteristic curves for films A and B are J-shaped, which is typical of industrial x-ray
film of types 1, 2, and 3. The curve for film C begins to flatten at a density between 3.0 and 3.5, giving it the S-shape
typical of type 4 x-ray films used with fluorescent screens.
Film speed is inversely related to the time required for a given intensity of radiation to produce a particular density on
the film; the shorter the exposure, the faster the film. In absolute units, film speed is inversely proportional to the total
energy (roentgens) of a particular radiation spectrum (wavelength distribution at a given kilovoltage) that produces a
given density on the film. For most practical applications, it is convenient and effective to deal with relative speeds. In
using relative speeds, film speeds are expressed in terms of the speed of one particular film whose relative speed is
arbitrarily assigned a value, for example, 100. Thus, if film A requires half the exposure of film B, the slower film (film
B) is chosen as the standard and assigned an arbitrary speed of 100. Film A, which is twice as fast, would have a relative
speed of 200.
To avoid making absolute measurements to determine film speed, it is convenient to refer to a group of film curves such
as those in Fig. 36(a). Curves positioned to the left of the chart require less exposure for a given density; those to the
right, more exposure. Thus, for a density of 2.0, film C in Fig. 36(a) is faster than film A, and both are faster than film B.
Their relative speed is calculated by determining the differences in log relative exposure and converting to the antilog.
Film B is the slowest film and requires a log relative exposure of 2.5 for a density of 2.0. Film B is chosen as the standard
and is assigned a speed of 100. Film A requires a log relative exposure of 1.9 for the same density. Subtracting 1.9 from
2.5 gives a difference of 0.6, for which the antilog is about 4, so the relative speed of film A is four times that of film B,
or has a relative speed of 400. Similarly, at a density of 2.0, film C requires a log relative exposure of 1.6. Subtracting 1.6
from 2.5 gives a log difference of 0.9, for which the antilog is about 8. Thus, film C is eight times faster than film B, or
has a relative speed of 800 at a density of 2.0.
Another advantage of using groups of characteristic curves is that the visual assessment of relative speeds can be easily
made. For example, although films A and B have similarly shaped curves running almost parallel, the curve for film C is
radically different. As calculated above, film C has a relative speed of 800 at a density of 2.0; however, at greater
densities, the relative speed of film C is lower than 800, and at lesser densities (down to a density of 1.0), the relative
speed of film C is greater than 800. Therefore, whenever relative speeds are used, the density at which they were
determined must be given.
Film gradient, also called film contrast, is a measure of the slope of the characteristic curve. If the difference is great,
the gradient (contrast) is said to be high. If the difference is slight, the gradient is said to be low. The contrast seen on a
radiograph is known as radiographic contrast and is composed of two factors:
•
Subject contrast, which is the result of variations in the amount of radiation absorbed by the testpiece
and which causes variations in radiation intensity impinging on the film
• Film gradient
(or film contrast), which is a measure of the response of the emulsion to the intensity of
impinging radiation and is a characteristic of a given film
Film gradient is determined from the characteristic curve by finding the slope of the curve at a given density. The slope of
the characteristic curve changes continuously over its entire length, as indicated in Fig. 36(a). The steeper the slope of the
curve over a range of relative exposures, the greater the difference in density and therefore the greater the resolution of
detail; thus, high gradient is important for good radiography.
In Fig. 36(b) tangents to a characteristic curve for a typical x-ray film have been drawn at two points, and the two
corresponding gradients (a/b and c/d) have been evaluated. Note that the gradient varies from 0.8 in the shallow portion of
the curve (called the toe) to 5 in the steeper portion of the curve.
Two regions of a testpiece that are slightly different in thicknesses will transmit slightly different intensities of radiation
to the film. On the characteristic curve, this would represent a small difference in the log relative exposure. For example,
assume that at a given kilovoltage the thinner section transmits 20% more radiation than the thicker section. The
difference in log relative exposure is 0.08 and is independent of tube current, exposure time, or source-to-film distance. In
the toe of the characteristic curve where, the gradient is only 0.8, the density difference is only 0.06, as indicated in Fig.
36(c). However, in the steeper portion of the curve where the gradient is 5, the density difference is 0.40. This effect of
film gradient is the main reason why it is best to use high exposures, obtaining the highest density that can be viewed on a
given illuminator for the greatest resolution of minor differences in transmitted radiation.
It is often more convenient to express gradient as an average over a given useful range of densities than for a single
density. This is a simple calculation in which the difference between the two densities is divided by the difference
between the log relative exposures for these densities; this ratio, known as the average gradient, is shown in Fig. 36(d).
Graininess. The silver halide grains that are contained in the emulsion of x-ray film are minute and can be seen only
with a high-power microscope, such as an electron microscope. Even though the emulsion on each side of the film is only
about 0.013 mm (0.0005 in.) thick, the grains are piled on top of each other in countless numbers. When the exposed-and-
processed radiograph is viewed, these small individual silver grains appear grouped together in relatively large masses.
This clumping, which is visible to the unaided eye or at low magnification, produces the visual impression called
graininess.

All films exhibit some degree of graininess. In general, slower films have less graininess than faster films. This general
relation is reflected in Table 6, which is an old classification scheme specified by the American Society for Testing and
Materials (ASTM) in the earlier 1984 edition of ASTM E 94. Although this classification scheme is somewhat arbitrary,
it is still sometimes specified in codes and specifications. Type 1 films have the least graininess, type 3 films exhibit the
most graininess, and type 2 films are intermediate.
Table 6 General characteristics of th
e four types of radiographic film specified in the earlier (1984) edition of
ASTM E 94
These groupings are given only for qualitative comparisons. For a more detailed discussion on film classification, see the section
"Film Types" in this article.
Film characteristic
Film type
Speed Gradient
Graininess
1 Low Very high
Very fine
2 Medium High
Fine
3 High Medium
Coarse
4
(a)
Very high
(b)
Very high
(b)
(c)
(a)
Normally used with fluorescent screens.
(b)
When used with fluorescent screens.
(c)
Graininess is mainly a characteristic of the fluorescent screens.
(d)
When used for direct exposure or with lead screens
The energy of the radiation also affects the graininess of films. As the penetrating capability of radiation increases
(photon energy increases and wavelength decreases), the graininess of all films increases, but the rate of increase may be
different for different films. As a result, it is possible that of two film types, one will show more graininess at long
wavelengths while the other shows more graininess at short wavelengths. The graininess of the images that are produced
at high photon energies makes the inherently fine-grain films such as types 1 and 2 particularly useful at photon energies
of 1 MeV or more.
Another source of graininess occurs in radiography using fluorescent intensifying screens. The graininess seen in
fluorescent-screen radiographs is primarily caused by the graininess that is inherent in the screen. This effect overshadows
the effect of film graininess, especially with films that are particularly sensitive to screen fluorescence. The graininess of
fluorescent-screen radiographs increases significantly with increased kilovoltage.
Lead screens have little effect on the graininess of the image; only slight increases in graininess at equal densities have
been noted when lead-screen radiographs are compared with direct radiographs made at the same photon energy.
Spectral Sensitivity. The shape of the characteristic curve of a given x-ray film is for all practical purposes unaffected
by the wavelength distribution in the x-ray or -ray beam used for the exposure. However, the sensitivity of the film in
terms of roentgens required to produce a given density is strongly affected by radiation energy (beam spectrum of a given
kilovoltage or given -ray source).
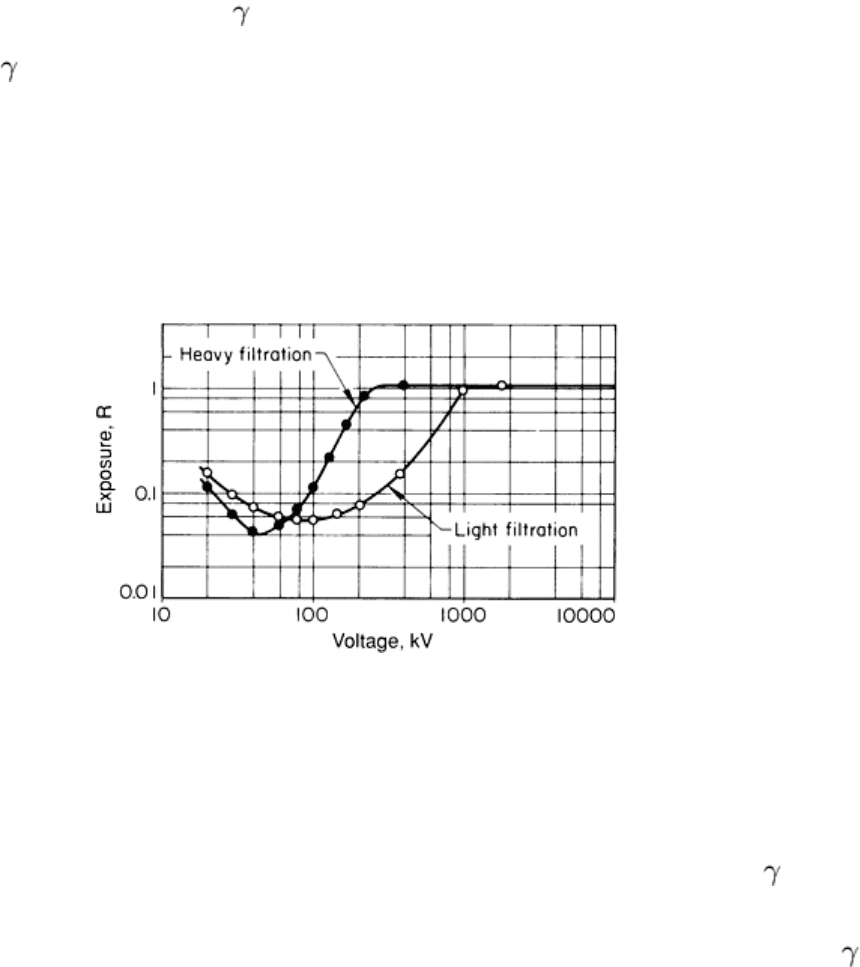
Figure 37 shows the exposure required for producing a density of 1.0 on radiographic film developed in an x-ray
developer for 5 min at 20 °C (68 °F). The exposures were made directly, without screens. The spectral-sensitivity curves
for all x-ray films have approximately the same general features as the curves shown in Fig. 37. The details, however,
differ from film to film; for example, the ratio of maximum-to-minimum sensitivity of the film to roentgens of exposure
varies. The details of the curves also differ with the degree that long wavelengths have been filtered from the beam (Fig.
37).
Fig. 37 Spectral-
sensitivity curves for a radiographic film showing exposure required to produce a density of
1.0
The spectral sensitivity of a given film, or the difference of spectral sensitivity between films, is usually considered in the
preparation of exposure charts and tables of relative speeds. For example, in tables of relative speeds, the speed of a
particular film usually varies with tube voltage. Also, in the preparation of exposure calculators for -rays, where
roentgens necessary to expose a given film to produce a given density are extensively used, spectral sensitivity is
important. As a result, manufacturers of radiographic film often furnish tables of spectral sensitivity for the films they
manufacture, indicating the roentgens required to produce several net densities at various x-ray tube voltages and -ray
photon energies.
Effect of Development on Film Characteristics. Although the shape of the characteristic curve is not affected by
variations in photon energy, it is affected by variations in the degree of development. The degree of development depends
on the type of developer used (including its degree of activity), temperature, and developing time. These factors are
discussed in the Appendix to this article. Within limits, an increased degree of development increases the speed and
gradient of a given film. If the limits are exceeded (that is, the film is overdeveloped), film speed based on density
(density above fog) no longer increases and may even decrease. Also, the fog (gray cloudiness) resulting from excessive
action of developer chemicals on unexposed grains will increase, and the gradient may decrease.
Figure 38 shows the characteristic curve of a radiographic film as affected by various times of manual development at 20
°C (68 °F) in an x-ray developer mixed from powder. As the developing time increases, the characteristic curve
progressively becomes steeper (gradient increases) and positioned more to the left on the chart (speed increases). It is
from such curves that values of relative speed and average gradient can be determined and developing recommendations
can be derived.
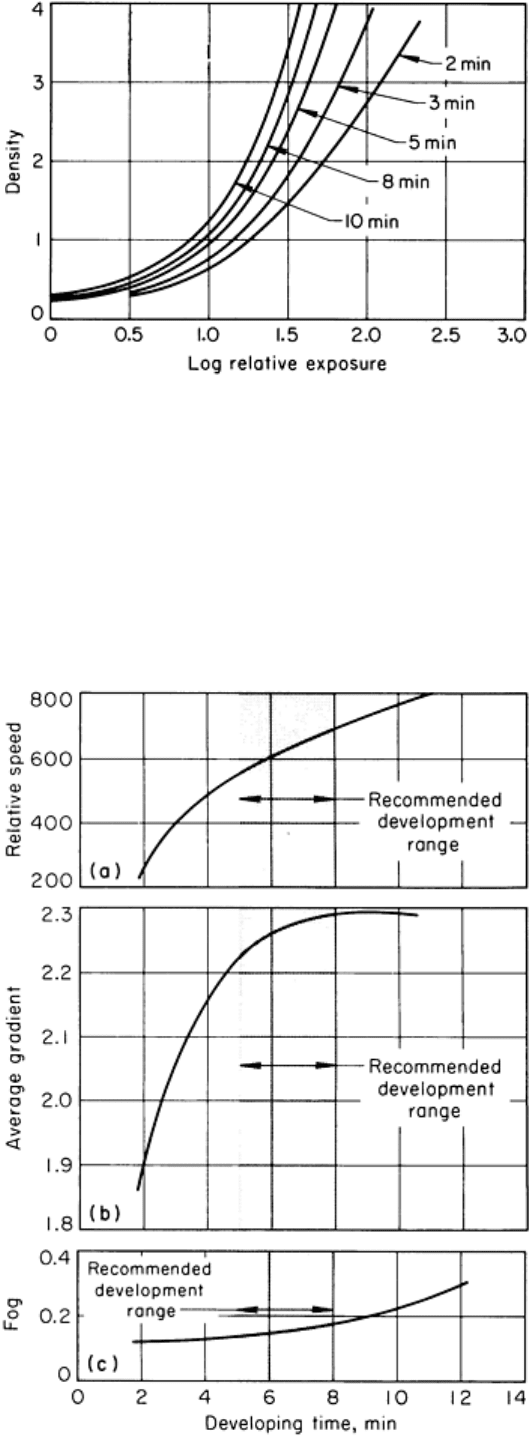
Fig. 38
Effect of various developing times on the characteristic curve of a radiographic film developed at 20 °C
(68 °F) in a manual process
Figure 39 shows the values of relative speed, average gradient, and fog plotted against developing time for the same film
and processing conditions detailed in Fig. 38. These curves indicate that at an 8-min developing time the average gradient
has reached its peak and further development would decrease film gradient. The speed, gradient, and fog curves of Fig. 39
are characteristic of this type of film, and similar curves are different for other types of films.
Fig. 39
Effect of developing time on (a) relative speed, (b) average gradient, and (c) fog for a radiographic
film. These graphs were derived from the same data as Fig. 38.
The degree of development also affects graininess. For example, if development time is increased to produce higher film
speed, the graininess is also increased. On the other hand, a developer or developing technique that gives an appreciable
reduction in graininess will also result in an appreciable loss of film speed. Adjustments in developing techniques made to
compensate for changes in temperature or in activity of a developer have little effect on graininess.
The variation of film gradient, speed, fog, and graininess with development time and temperature for a given radiographic
film and developer solution makes it imperative that standardized procedures for development of radiographic film be
meticulously followed. Unless this is done, it is impossible to obtain consistent resolution of variations in radiation
intensity. Inconsistency in the resolution of variations in radiation intensity can seriously impair the ability to detect flaws
in metals.
Film Types and Selection
The selection of radiographic film for a particular application is generally a compromise between the desired quality of
the radiograph and the cost of exposure time. This compromise occurs because slower films generally provide a higher
film gradient and a lower level of graininess and fog.
Film Types. The classification of radiographic film is complicated, as evidenced by changes in ASTM standard practice
E 94. The 1988 edition of ASTM E 94 references a new document (ASTM E 746-87), which describes a standard test
method for determining the relative image-quality response of industrial radiographic film. Careful study of this
document is required to arrive at a conclusive classification index suitable for the given radiographic film requirements of
a facility.
Earlier editions (1984 and prior) of ASTM E 94 contained a table listing the characteristics of industrial films grouped
into four types. The general characteristics of these four types are summarized in Table 6. This relatively simple
classification method is referenced by many codes and specifications, which may state only that a type 1 or 2 film can be
used for their specification requirements. However, because of this relatively arbitrary method of classification, many
film manufacturers may be reluctant to assign type numbers to a given film. Moreover, the characteristics of radiographic
films can vary within a type classification of Table 6 because of inherent variations among films produced by different
manufacturers under different brand names and because of variations in film processing that affect both film speed and
radiographic density. These variations make it essential that film processing be standardized and that characteristic curves
for each brand of film be obtained from the film manufacturer for use in developing exposure charts.
Because the variables that govern the classification of film are no longer detailed in ASTM E 94-88, it is largely the
responsibility of the film manufacturer to determine the particular type numbers associated with his brand names. Some
manufacturers indicate the type number together with the brand name on the film package. If there is doubt regarding the
type number of a given brand, it is advisable to consult the manufacturer. Most manufacturers offer a brand of film
characterized as very low speed, ultrahigh gradient, and extremely fine grain.
Film selection for radiography is a compromise between the economics of exposure (film speed and latitude) and the
quality desired in the radiograph. In general, fine-grain, high-gradient films produce the highest-quality radiographs.
However, because of the low speed typically associated with these films, high-intensity radiation or long exposure times
are needed. Other factors affecting radiographic quality and film selection are the type and thickness of the testpiece and
the photon energy of the incident radiation.
Although the classification of film is more complex than the types given in Table 6, a general guide is that better
radiographic quality will be promoted by the lowest type number in Table 6 that economic and technical considerations
will allow. In this regard, Table 7 suggests a general comparison of film characteristics for achieving a reasonable level of
radiographic quality for various metals and radiation-source energies. It should be noted, however, that the film types are
only a qualitative ranking of the general film characteristics given in Table 6. Many radiographic films, particularly those
designed for automatic processing, cannot be adequately classified according to the system in Table 6. This compounds
the problem of selecting film for a particular application.

Table 7 Guide to the selection of radiographic film for steel, aluminum, bronze, and magnesium in various
thicknesses
Thickness
Type of film
(a)
for use with these x-ray tube voltages, or radioactive isotopes:
mm (in.) 50-80
kV
80-120
kV
120-150
kV
150-250
kV
Ir-192
250-400
kV
1
MeV
Co-60
2
MeV
Ra
6-31
MeV
Steel
0-6
(0- )
3 3 2 1 . . . . . . . . . . . . . . . . . .
. . .
6-13
( - )
4 3 2 2 . . . 1 . . . . . . . . . . . .
. . .
13-25
( -1)
. . . 4 3 2 2 2 1 . . . 1 2
. . .
25-50 (1-2) . . . . . . . . . 3 2 2 1 2 1 2
1
50-100 (2-4) . . . . . . . . . 4 3 4 2 2 2 3
1
100-200
(4-8) . . . . . . . . . . . . . . . 4 3 3 2 3
2
>200 (>8) . . . . . . . . . . . . . . . . . . . . . . . . 3 . . .
2
Aluminum
0-6
(0- )
1 1 . . . . . . . . . . . . . . . . . . . . . . . .
. . .
6-13
( - )
2 1 1 1 . . . . . . . . . . . . . . . . . .
. . .
13-25
( -1)
2 1 1 1 . . . 1 . . . . . . . . . . . .
. . .
25-50 (1-2) 3 2 2 1 1 1 . . . . . . . . . . . .
. . .
50-100 (2-4) 4 3 2 2 1 2 . . . . . . . . . . . .
. . .
100-200
(4-8) . . . 4 3 3 2 3 . . . . . . . . . . . .
. . .
>200 (>8) . . . . . . . . . . . . 4 . . . . . . . . . . . . . . .
. . .
Bronze
0-6
(0- )
4 3 2 1 1 1 1 . . . . . . . . .
. . .
6-13
( - )
. . . 3 2 2 2 1 1 . . . 1 . . .
. . .
13-25
( -1)
. . . 4 4 3 2 2 1 2 1 2
. . .
25-50 (1-2) . . . . . . 4 4 3 3 1 2 1 2
1
50-100 (2-4) . . . . . . . . . . . . 3 4 2 3 2 3
1
100-200
(4-8) . . . . . . . . . . . . . . . . . . 3 3 2 . . .
2
>200 (>8) . . . . . . . . . . . . . . . . . . . . . . . . 3 . . .
2
Magnesium
0-6
(0- )
1 1 . . . . . . . . . . . . . . . . . . . . . . . .
. . .
6-13
( - )
1 1 1 . . . . . . . . . . . . . . . . . . . . .
. . .
13-25
( -1)
2 1 1 . . . 1 . . . . . . . . . . . . . . .
. . .
25-50 (1-2) 2 1 1 1 1 . . . . . . . . . . . . . . .
. . .
50-100 (2-4) 3 2 2 1 2 . . . . . . . . . . . . . . .
. . .
100-200
(4-8) . . . 3 2 2 3 . . . . . . . . . . . . . . .
. . .
>200 (>8) . . . . . . . . . 4 . . . . . . . . . . . . . . . . . .
. . .
(a)
These recommendations represent a usually acceptable level of radiographic quality and are based on the qualitative classification of films
defined in Table 6. Optimum radiographic quality will be promoted by use of the lowest-number film type that economic and technical
considerations will allow. The recommendations for type 4 film are based on the use of fluorescent screens.
Film latitude, which is the range of testpiece thickness that can be recorded with a single exposure, also influences film
selection (see the following section in this article for a discussion of latitude). High-gradient films generally have narrow
latitude, that is, only a narrow range of testpiece thickness can be imaged with optimum density for interpretation. If the
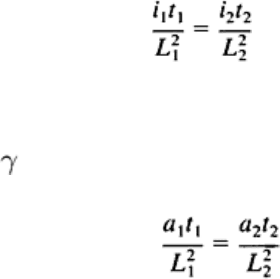
testpiece is of nonuniform thickness, more than one exposure may have to be made (using different x-ray spectra or
different exposure times) for complete inspection of the piece. The number of exposures, as well as the exposure times,
can often be reduced by using a faster film of lower gradient but wider latitude, although there is usually an
accompanying reduction in ability to image small flaws.
Exposure Factors
The exposure time in film radiography depends mainly on film speed, the intensity of radiation at the film surface, the
characteristics of any screens used, and the desired level of photographic density. In practice, the energy of the radiation
is first chosen to be sufficiently penetrating for the type of material and thickness to be inspected. The film type and the
desired photographic density are then selected according to the sensitivity requirements (Eq 2) for recording the expected
variations in the intensity of the transmitted radiation. Once these factors are fixed, then the source strength, the source-to-
film distance, and the characteristics of any screens used determine the exposure time.
With a given type of film and screen, the exposure time to produce the desired photographic density obeys the reciprocity
law for equivalent exposures (Eq 5). The reciprocity law can be modified to include the inverse-square law (Eq 13),
which models the relation between radiation intensity at the film and the source-to-film distance. Therefore, because the
intensity is inversely proportional to the square of distance from the source according to Eq 13, the reciprocity law for
equivalent exposures with an x-ray tube (Eq 5) can be rewritten as:
(Eq 16)
where i is the tube current, t is the exposure time, L is the source-to-film distance, and the subscripts refer to two different
combinations that produce images with the desired photographic density. The parallel expression that applies to exposures
made with a -ray source is:
(Eq 17)
where a is the source strength in gigabecquerel (curies).
For practical applications using the same quality of x-rays (same kilovoltage) or the same radioactive source, Eq 16 or 17
is applied in the following manner. If a satisfactory radiograph of a given testpiece can be obtained at a 1 m (3.3 ft)
source-to-film distance, 20-mA tube current, and 10-s exposure time, an equivalent radiograph can be obtained in 6.4 s
with 20-mA tube current or in 8 s with 16-mA tube current when the distance is reduced to 0.8 m (2.6 ft). However, if the
source-to-film distance is increased to 2 m (6.6 ft), it will take 40 s at 20 mA or 32 s at 25 mA or 16 s at 50 mA to
produce equivalent film density.
Similarly, if a satisfactory radiograph can be obtained with a 440 GBq (12 Ci) cobalt-60 source at 1 m (3.3 ft) source-to-
film distance in 20 min, a radiograph of equivalent density will require a 45-min exposure time with the same 440 GBq
(12 Ci) source if the distance is increased to 1.5 m (4.9 ft).
Exposure Charts for X-Ray Radiography. A starting point must be determined for the calculations described in the
discussions above. The starting point is ordinarily derived from exposure charts of the type shown in Fig. 40. Equipment
manufacturers usually publish exposure charts for each type of x-ray generator that they manufacture. These published
charts, however, are only approximations; each particular unit and each installation is unique. Radiographic density is
affected by such factors as radiation spectrum, film processing, setup technique, amount and type of filtration, screens,
and scattered radiation.
