ASM Metals HandBook Vol. 14 - Forming and Forging
Подождите немного. Документ загружается.

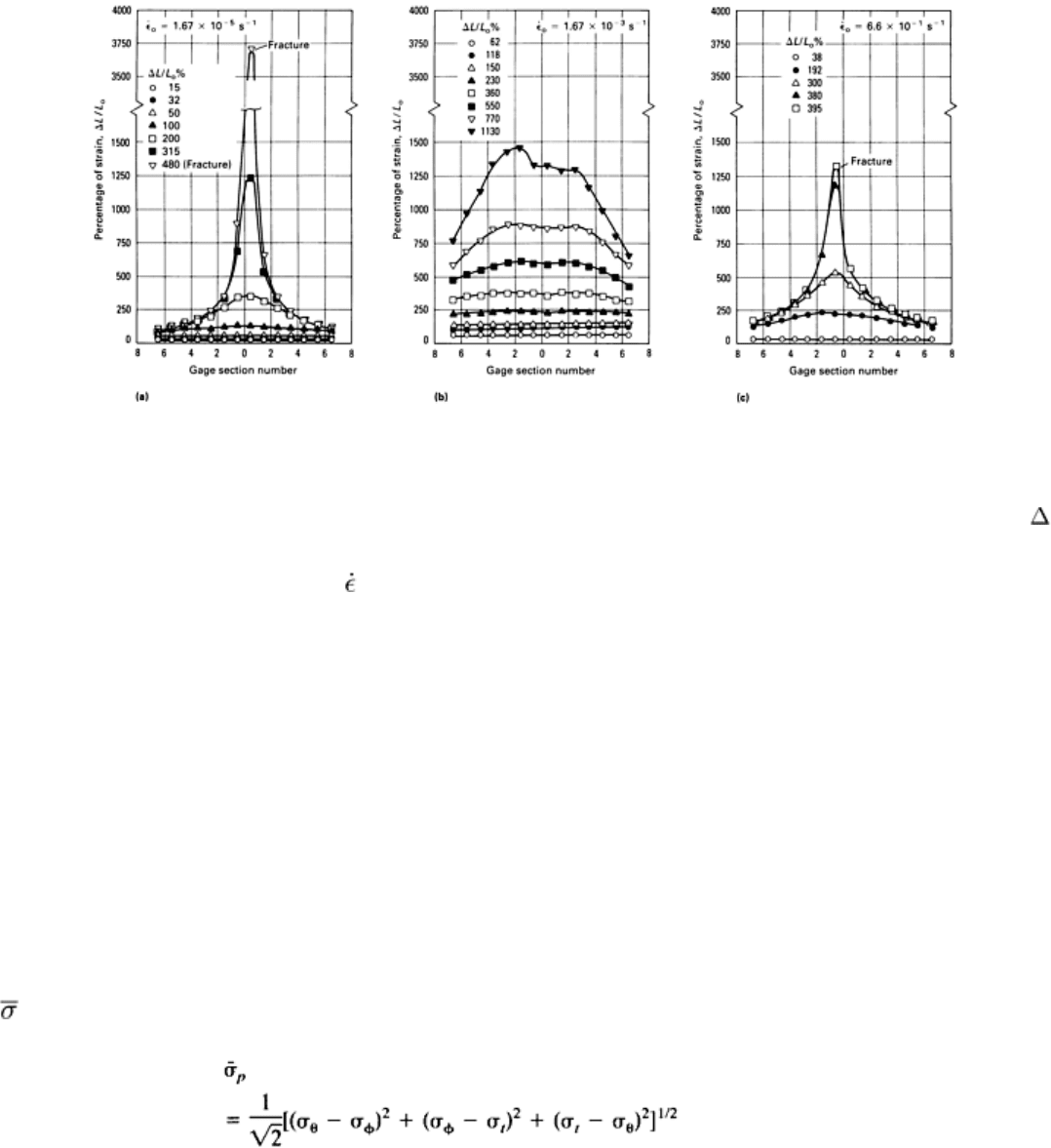
Fig. 21 Local elongation gradients in tensile specimens of Zn-22Al alloy at T = 473 K with initial gage length L
o
of 12.7 mm (0.500 in.) that were tested within the superplastic strain rate range (b) and outside the
superplastic strain rate range (a) and (c). The total percentage of strain at each termination point is given by
L/L
o
, where ΔL
is the overall increase in gage length. The percentage of strain in each of the 14 individual
segments of the gage length is given by Δl/l
o
%, where Δl
is the increase in length of each small segment of the
specimen. The initial strain rate was
o
.
Spherical Domes. Although the thinning in superplastic tensile test specimens is the result of geometric
inhomogeneities, the corresponding thinning in biaxially formed parts is usually the result of local stress state differences,
which subsequently lead to the development of geometric inhomogeneities. In all of these cases, however, the difference
in the local stresses leads to strain rate gradients, and the strain rate gradients develop directly into thickness gradients. A
major difference between the tensile specimen and the part configuration is that, in the former, the stress gradients can be
varied (that is, reduced) by dimensional control during machining. In the part forming, however, the configuration
determines the stress state, and the stress state is not adjustable without changing the geometry.
The concept of thinning during SPF processing is perhaps best understood in terms of the bulging of a sheet (Ref 25, 26,
30, 40, 41, 42, 43, 44, 45, and 46). In this geometry, there is a stress state gradient from the pole of the dome to the edge,
as shown in Fig. 22. If the dome is assumed to develop into a part of spherical symmetry, the stress state can be readily
described. At the pole, the orthogonal stresses are equal, and the stress state is that of equibiaxial tensile. At the edge of
the dome, there is constraint around the periphery, leading to a plane-strain stress state. Because the flow behavior of
superplastic metals has been found to obey the von Mises criterion (Ref 47), it is helpful to examine the effective stress,
, which will determine the corresponding strain rate:
(Eq 10)
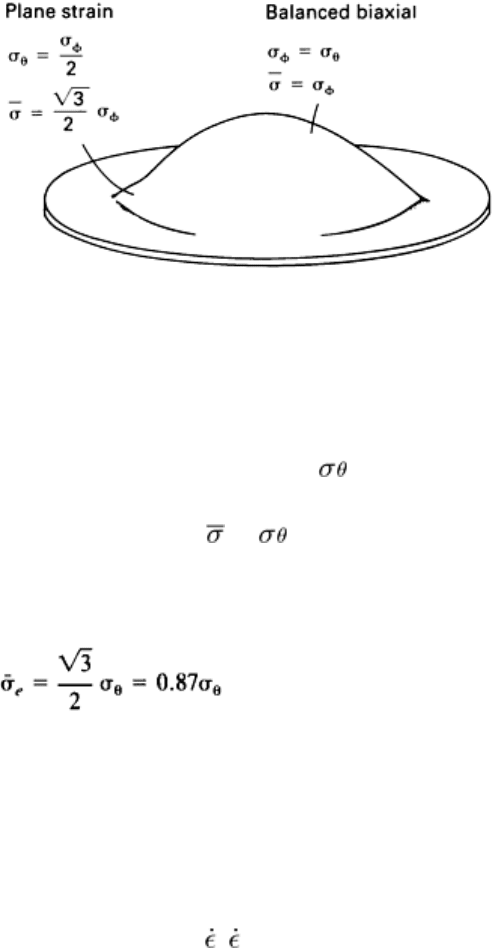
Fig. 22 Illustration of a spherical dome indicating the range of stress states
existing between the pole and the
edge
If it is assumed that the through-thickness stress is small with respect to the in-plane stresses, the effective stresses at the
pole and the edge can be expressed in terms of the meridional stress, , as follows:
p
=
and
(Eq 11)
where the subscripts p and e indicate the pole and the edge, respectively, of the dome. Therefore, the pole is experiencing
a 15% higher flow stress than the edge, resulting in a higher strain rate, the initial magnitude of which depends on the m
value.
The stress state difference between the pole and the edge of the dome is roughly the equivalent of the tensile specimen,
which has a local geometric inhomogeneity, f, of 0.13. The initial strain rate difference between these two areas is
dependent on the m value, the larger the m value, the smaller the strain rate difference and the less the tendency to
develop a thickness gradient. For example, the ratio of
e
/
p
is 0.87 for m = 1, and the value is 0.5 for m = 0.2--both for
the same initial effective stress difference.
Therefore, the stress gradient in a forming dome causes a more rapid thinning rate at the pole, and it may be expected that
the thinning difference will accelerate with time, leading to a thickness gradient in the formed dome. There are abundant
experimental results to show that this is the case and that the thinning gradient is a function of the m value. Profiles of
thickness for bulge-formed sheets are shown in Fig. 23 for m values of 0.57 and 0.23 (Ref 40). The thickness gradient is
in agreement with expectations, and the effect of the high m value in impeding localized thinning at the pole can be seen.
Other results for a titanium alloy and a stainless steel for which m values are 0.75 and 0.4, respectively, are shown in Fig.
24, in which the thickness strain is plotted as a function of the position along the dome cross section (Ref 21). The
position along the dome is measured as the fractional height, h/h
o
, where h
o
is the full height of the dome and h is the
height on the dome at which the thickness measurement is made.
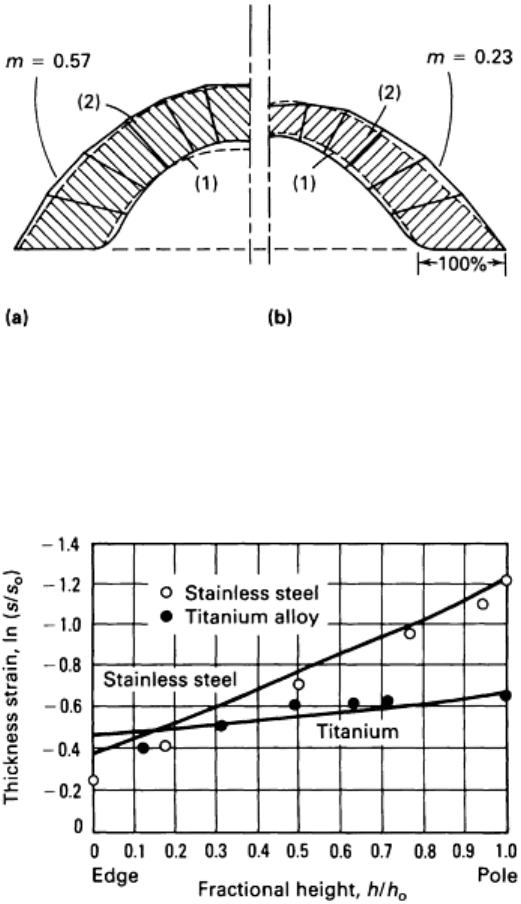
Fig. 23
Experimentally observed thickness profiles for a hemispherical dome formed from materials with two
different m v
alues (solid lines). The smaller, broken outlines confined mainly within the experimental data
silhouette represent bulge profiles (1) and sheet thickness distributions (2) that were calculated using m
= 0.50
(a) and m = 0.20 (b).
Fig. 24 Thickness strain as a function of the fractional height for dome-
shaped parts formed from a stainless
steel with an m value of 0.4 and a titanium alloy with an m value of 0.75. The values s and s
o
in ln(s/s
o
)
represent dome thickness and initial sheet thickness, respectively.
A number of analytical developments have been reported that predict the thinning for the superplastic forming of this type
of geometry (Ref 26, 30, 42, 44, 45, and 46). These models result in relations for thicknesses that are not closed-form, but
require numerical integration of strain increments. The models predict the thinning characteristics reasonably well, as can
be seen by the comparison of experimental and analytical data shown in Fig. 24 and 25.
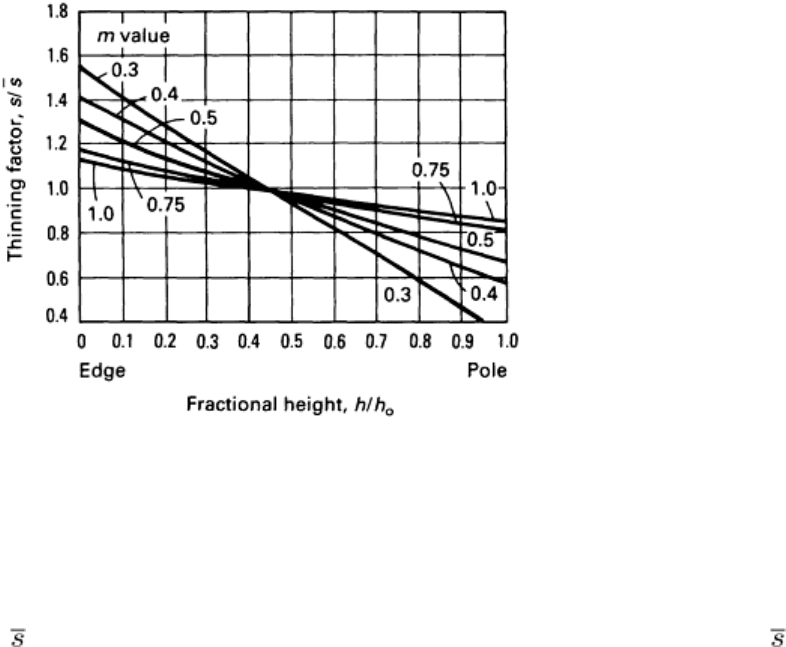
Fig. 25
Theoretical relations for a hemisphere showing the thinning factor as a function of the fractional height
for a range of m values from 0.3 to 1.0
The theoretical predictions can be used to show the influence of the strain rate sensitivity of flow stress on the thinning
gradient. For example, the thinning for a hemisphere formed from materials of differing m values is illustrated in Fig. 25.
In Fig. 25, the thinning factor s/ is plotted as a function of the fractional height, where s is the local thickness and is
the average dome thickness. The maximum thinning occurs at the pole because of the stress state, as mentioned
previously, and the strain rate sensitivity is a crucial parameter in determining not only the initial strain rate difference but
also the subsequent rate of thinning, as shown in Fig. 26, in which the thinning factor at the pole can be seen to be
increasingly influenced by m as the dome height is increased.
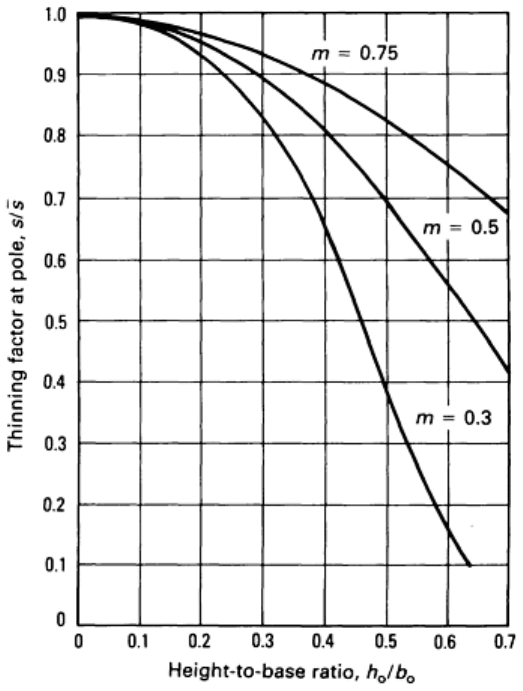
Fig. 26 Theoretical curves showing the thinning factor at the pole as a function of the bulge height-to-
base
ratio for m = 0.3, 0.5, and 0.75
The initial stress state differences and the corresponding strain rate differences along the meridian of a forming dome lead
to a predictable thinning gradient in this type of geometry. The magnitude of the thinning gradient, however, is
determined by the strain rate sensitivity, m, and the height to which the part is formed.
Rectangular Shapes. The factors that contribute to the thinning characteristics in rectangular parts, as well as other
shapes, are the same as those for the spherical dome-shaped parts discussed in the previous section in this article. It is the
specific geometry that determines the initial stress state gradients, and different geometries will be expected to develop
different stress states in the forming part.
The rectangular shape is one that is common to many parts or sections of parts; therefore, it has been studied by
experimental and analytical methods similar to those used for the spherical dome (Ref 22, 27, 47). For the long
rectangular shape, there is a plane-stress state throughout the width of the sheet; for the case in which the die entry radius
does not cause a significant stress concentration, the sheet will not experience an initial stress state gradient. This case is
very similar to that of the tensile test, in which only thickness variations or material inhomogeneities will cause local
stress differences leading to localized thinning. Because these are small in comparison to the magnitude of the stress
variation in the forming dome, it may be expected that the thinning gradients would be less pronounced. Experimental
results for the free-forming cylindrical section show this to be the case, as illustrated in Fig. 27, and virtually no thinning
gradient is seen for hemicylindrical shapes.
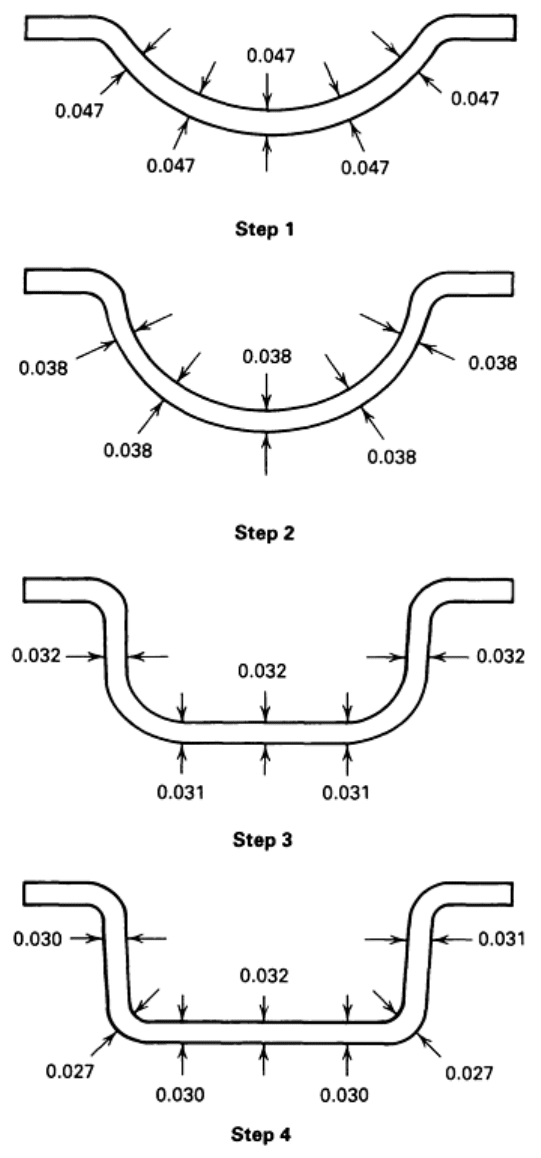
Fig. 27 Thinning development in a 1.37 mm (0.054 in.) thick superplastic formed Ti-6Al-
4V part having a
rectangular cross section and semi-
infinite length. Formed at 870 °C (1600 °F) using a boron nitride lubricant,
the sheet required 20 min to fabricate at an average strain rate of 5.8 × 10
-4
. Dimensions given in inches
Interactions with the tooling do, however, cause local stress variations that can lead to thinning gradients, as shown in Fig.
27. This effect can be considered as two different types resulting from different areas of the die--the die surface at the
bottom and sidewall, and the die entry radius.

Die Bottom and Sidewall. Ignoring the die entry effects, the die surface can be considered to restrict deformation in
the forming sheet where contact has been made and where friction is non-zero. If the friction is large, the forming
characteristic is as illustrated in Fig. 28. When the sheet makes contact with the die wall surface, the deformation in that
contact area is restricted, and thinning is localized in the noncontact areas, leading to a greater degree of thinning in the
last area to contact the die than in the first areas to make contact (Fig. 28). This results in a thickness gradient, as shown in
Fig. 29, for a titanium alloy part formed in a die with no lubricating compounds present.
Fig. 28 Illustration of thinning characteristics in the blow form
ing of an unlubricated part of rectangular cross
section and semi-infinite length
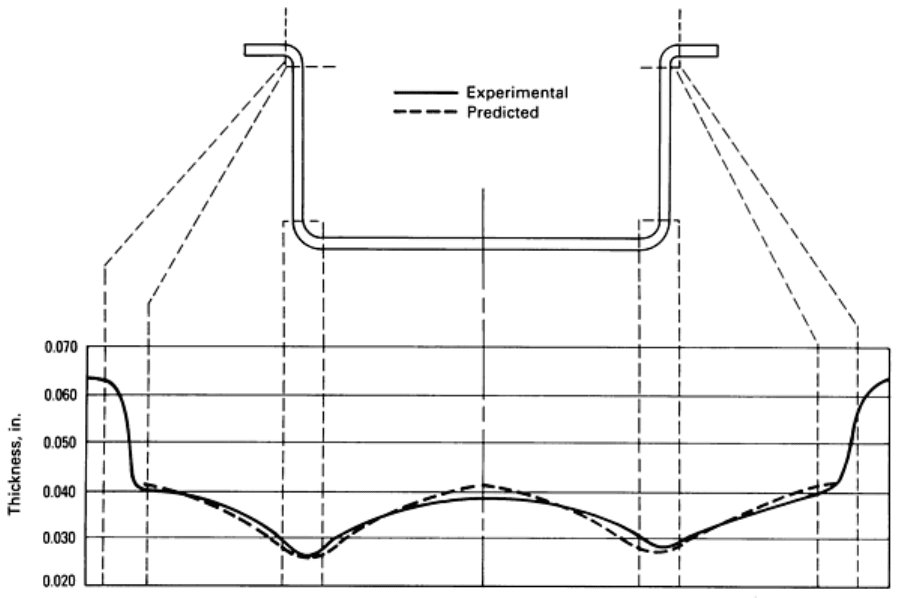
Fig. 29 Observed and predicted thinning profiles in an unlubricated blow-formed Ti-6Al-
4V alloy part of
rectangular cross section. Forming of the sheet, which had an initial thickness of 1.68 mm (0.066 in.), required
20 min at 925 °C (1700 °F).
This type of thinning is readily predicted analytically if it is assumed that the sheet sticks to the die surface after contact is
made by using an incremental method (Ref 27). Results of this type of model show that there are a variety of thinning
variations corresponding to various width and depth ratios of the rectangular shape, as shown in Fig. 30. It is apparent
from Fig. 30 that the narrow and deep parts develop the greatest amount of thinning. In this specific case, the thickness
profiles can be predicted quite well without referring to the strain rate sensitivity, m. This is the result of the dominant
effect of the die friction coupled with the uniform initial stress state.
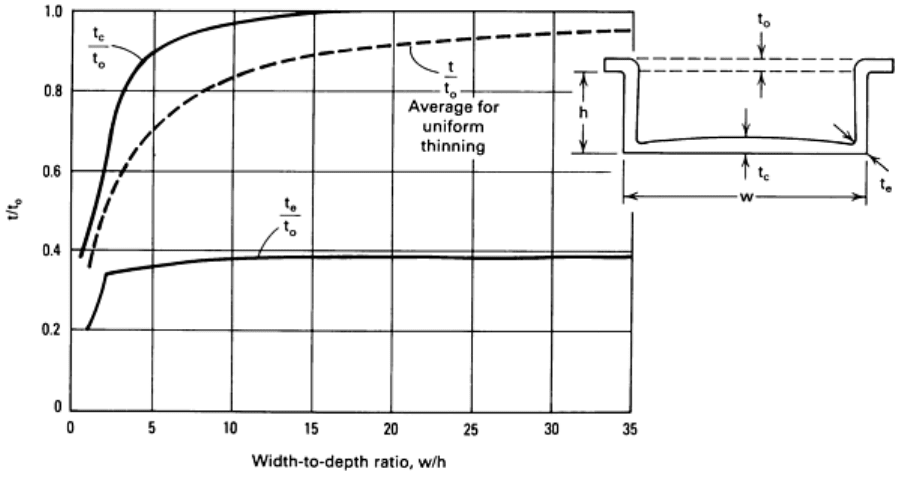
Fig. 30 Predicted minimum thicknesses as function of the width-to-depth (w/h) ratio for unlubricated blow-
forming part of rectangular cross section.
If the interfacial friction is reduced, the thinning gradient will be reduced in the sidewall and bottom areas because
continued deformation after die contact is possible. An example of the thinning in a formed rectangular titanium part is
shown in Fig. 31, for which forming was conducted with a boron nitride solid lubricant (Ref 22, 27).
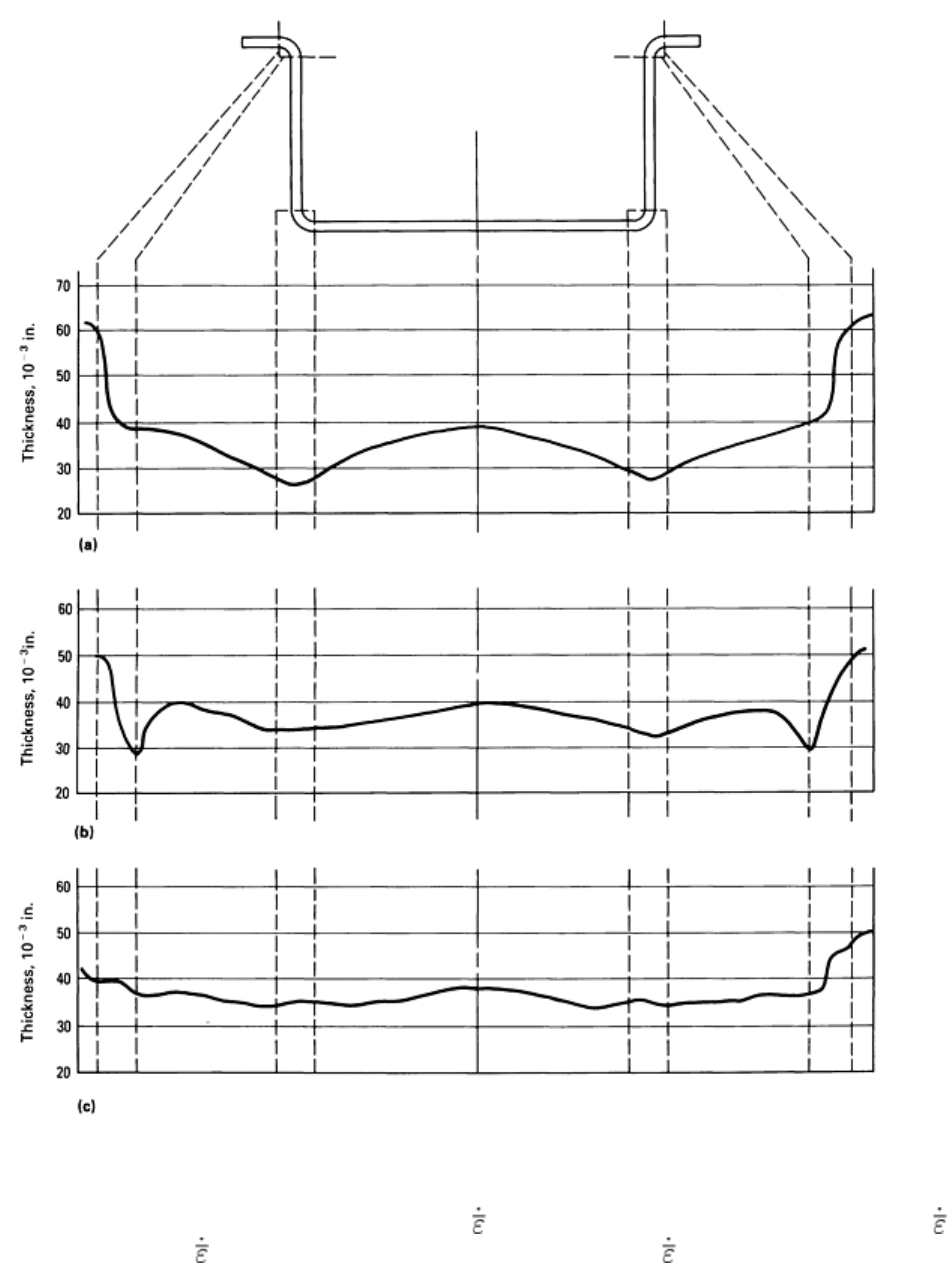
Fig. 31 Observed thickness profiles for 1.68 mm (0.066 in.) thick Ti-6Al-4V blow-formed p
arts of rectangular
cross section formed under different average strain rates,
t
, and with different lubrication conditions. (a)
t
= -
7 × 10
-4
s
-1
no lubricant. (b)
t
= -5.6 × 10
-4
s
-1
; boron nitride lubricant. (c)
t
= -5.4 × 10
-5
s
-1
; boron nitride
lubricant
A die entry radius causes a local stress concentration in the forming sheet, which then creates a stress state gradient in
the forming sheet, and this can lead to localized thinning, especially if the ratio of die radius to sheet thickness is small
and if the surface is lubricated. The source of the stress concentration is the back pressure exerted by the die radius on the
forming sheet and the gas pressure on the opposite side of the sheet from the die. The pressure exerted by the die radius
has been shown to be (Ref 27):
