Askeland D.R., Fulay P.P. Essentials of Materials Science & Engineering

Подождите немного. Документ загружается.

Although the handle could be a lightweight, tough compo site material

(such as a polymer reinforced with Kevlar (a special polymer) ﬁbers), a wood

handle about 70 cm long would be much less expensive and would still provide

su‰cient toughness. As shown in a later chapter, wood can be categorized as a

natural ﬁber-reinforced composite.

To produce the head, we prefer a material that has a low transition tem-

perature, can absorb relatively high energy during impact, and yet also has

enough hardness to avoid deformation. The toughness requirement would rule

out most ceramics. A face-centered cubic metal, such as FCC stainless steel or

copper, might provide superior toughness even at low temperatures; however,

these metals are relatively soft and expensive. An appropriate choice might be

a normal BCC steel. Ordinary steels are inexpensive, have good hardness and

strength, and some have su‰cient toughness at low temperatures.

In Appendix A, we ﬁnd that the density of iron is 7.87 g/cm

. We assume

that the density of steel is about the same. The volume of steel required is

V ¼

3:6  10

7:87 g=cm

¼ 0:46  10

: To assure that we will hit our target, the

head might have a cylindrical shape, with a diameter of 6.25 cm. The length of

the head would then be 15 cm.

SUMMARY

V The mechanical behavior of materials is described by their mechanical properties,

which are measured with idealized, simple tests. These tests are designed to repre-

sent di¤erent types of loading conditions. The properties of a material reported in

various handbooks are the results of these tests. Consequently, we should always

remember that handbook values are average results obtained from idealized tests

and, therefore, must be used with care.

V The tensile test describes the resistance of a material to a slowly applied stress. Im-

portant properties include yield strength (the stress at which the material begins

to permanently deform), tensile strength (the stress corresponding to the maximum

applied load), modulus of elasticity (the slope of the elastic portion of the stress-

strain curve), and % elongation and % reduction in area (both, measures of the

ductility of the material).

V The bend test is used to determine the tensile properties of brittle materials. A

modulus of elasticity and a ﬂexural strength (similar to a tensile strength) can be

obtained.

V The hardness test measures the resistance of a material to penetration and provides

a measure of the wear and abrasion resistance of the material. A number of

hardness tests, including the Rockwell and Brinell tests, are commonly used. Often

the hardness can be correlated to other mechanical properties, particularly tensile

strength.

V The impact test describes the response of a material to a rapidly applied load. The

Charpy and Izod tests are typical. The energy required to fracture the specimen is

measured and can be used as the basis for comparison of various materials tested

under the same conditions. In addition, a transition temperature above which the

material fails in a ductile, rather than a brittle, manner can be determined.

C HA P T E R 6 Mechanical Properties: Fundamentals and Testing180

GLOSSARY

Anelastic (viscoelastic) material A material in which the total strain developed has elastic and

viscous components. Part of the total strain recovers similar to elastic strain. Some part, though,

recovers over a period of time. Examples of viscoelastic materials: polymer melts, many polymers

including Silly Putty

. Typically, the term anelastic is used for metallic materials.

Bend test Application of a force to the center of a bar that is supported on each end to de-

termine the resistance of the material to a static or slowly applied load. Typically used for brittle

materials.

Compliance Inverse of Young’s modulus or modulus of elasticity.

Dilatant (shear thickening) Materials in which the apparent viscosity increases with the in-

creasing rate of shear.

Ductile to brittle transition temperature (DBTT) The temperature below which a material be-

haves in a brittle manner in an impact test. The ductile to brittle switchover also depends on the

strain rate.

Ductility The ability of a material to be permanently deformed without breaking when a force is

applied.

Elastic deformation Deformation of the material that is recovered instantaneously when the

applied load is removed.

Elastic limit The magnitude of stress at which the relationship between stress and strain begins

to depart from linearity.

Elastic strain Fully and instantaneously recoverable strain in a material.

Elastomers Natural or synthetic polymeric materials that are comprised of molecules with

spring-like coils that lead to large elastic deformations (e.g., natural rubber, silicones).

Engineering strain The amount that a material deforms per unit length in a tensile test.

Engineering stress The applied load, or force, divided by the original cross-sectional area of the

material.

Extensometer An instrument to measure change in length of a tensile specimen, thus allowing

calculation of strain.

Flexural modulus The modulus of elasticity calculated from the results of a bend test, giving the

slope of the stress-deﬂection curve.

Flexural strength The stress required to fracture a specimen in a bend test. Also called the

modulus of rupture.

Glass temperature (T

) A temperature below which an otherwise ductile material behaves as if

it is brittle. Usually, this temperature is not ﬁxed and is a¤ected by processing of the material.

Hardness test Measures the resistance of a material to penetration by a sharp object. Common

hardness tests include the Brinell test, Rockwell test, Knoop test, and Vickers test.

Hooke’s law The relationship between stress and strain in the elastic portion of the stress-strain

curve.

Impact energy The energy required to fracture a standard specimen when the load is applied

suddenly.

Impact loading Application of stress at a very high strain rate (@>100 s

1

Impact test Measures the ability of a material to absorb the sudden application of a load

without breaking. The Charpy and Izod tests are the commonly used impact tests.

Glossary 181

Impact toughness Energy absorbed by a material, usually notched, during fracture, under the

conditions of an impact test.

Kinematic viscosity (m) Ratio of viscosity and density, often expressed in centiStokes.

Load The force applied to a material during testing.

Materials processing Manufacturing or fabrication methods used for shaping of materials (e.g.,

extrusion, forging).

Macrohardness Overall bulk hardness of materials measured using loads >2N.

Microhardness Hardness of materials typically measured using loads less than 2 N using such

test as Knoop (HK).

Modulus of elasticity (E ) Young’s modulus, or the slope of the linear part of the stress-strain

curve in the elastic region. It is a measure of the sti¤ness of a material, depends upon strength of

interatomic bonds and composition, and is not strongly dependent upon microstructure.

Modulus of resilience (E

) The maximum elastic energy absorbed by a material when a load is

applied.

Modulus of rupture The stress required to fracture a specimen in a bend test. Also called the

ﬂexural strength.

Nano-hardness Hardness of materials measured at 1–10 nm length scale using extremely small

(@100 mN) forces.

Necking Local deformation causing reduction in the cross-sectional area of a tensile specimen.

Many ductile materials show this behavior. The engineering stress begins to decrease at the onset

of necking.

Newtonian Materials in which the shear stress and shear strain rate are linearly related (e.g.,

light oil or water).

Non-Newtonian Materials in which shear stress and shear strain rate are not linearly related,

these materials are shear thinning or shear thickening (e.g., polymer melts, slurries, paints, etc.).

Offset strain value A value of strain (e.g., 0.002) used to obtain the o¤set yield stress value.

Offset yield strength A stress value obtained graphically that describes the stress that gives no

more than a speciﬁed amount of plastic deformation. Most useful for designing components.

Also, simply stated as the yield strength.

Percent elongation The total percentage increase in the length of a specimen during a tensile test.

Percent reduction in area The total percentage decrease in the cross-sectional area of a speci-

men during the tensile test.

Plastic deformation or strain Permanent deformation of a material when a load is applied, then

removed.

Poisson’s ratio The ratio between the lateral and longitudinal strains in the elastic region.

Proportional limit A level of stress above which the relationship between stress and strain is not

linear.

Pseudoplastics (shear thinning) Materials in which the apparent viscosity decreases with in-

creasing rate of shear.

Shear modulus (G) The slope of the linear part of the shear stress-shear strain curve.

Shear-strain rate Time derivative of shear strain. See Strain rate.

Stiffness A qualitative measure of the elastic deformation produced in a material. A sti¤ mate-

rial has a high modulus of elasticity. Sti¤ness also depends upon geometry.

C HA P T E R 6 Mechanical Properties: Fundamentals and Testing182

Strain Elongation change in dimension per unit length.

Strain gage A device used for measuring change in length and hence strain.

Strain rate The rate at which strain develops in or is applied to a material indicated as

e or

g for

tensile and shear-strain rates, respectively. Strain rate can have an e¤ect on whether a material

would behave in a ductile or brittle fashion.

Stress Force or load per unit area of cross-section over which the force or load is acting.

Stress relaxation Decrease in the stress for a material held under constant strain, as a function

of time, observed in viscoelastic materials. Stress relaxation is di¤erent from time dependent re-

covery of strain.

Tensile strength The stress that corresponds to the maximum load in a tensile test.

Tensile test Measures the response of a material to a slowly applied uniaxial force. The yield

strength, tensile strength, modulus of elasticity, and ductility are obtained.

Tensile toughness The area under the true stress-true strain tensile test curve. It is a measure of

the energy required to cause fracture under tensile test conditions.

True strain The strain calculated using actual and not original dimensions, given by e

¼ lnðl=l

Þ.

True stress The load divided by the actual cross-sectional area of the specimen at that load.

Viscoelastic (or anelastic) material See Anelastic material.

Viscosity (h) Measure of resistance to ﬂow, deﬁned as the ratio of shear stress to shear strain

rate (units Poise or Pa-s).

Viscous material A viscous material is one in which the strain develops over a period of time

and the material does not go to its original shape after the stress is removed.

Work of fracture Area under the stress-strain curve, considered as a measure of tensile toughness.

Yield point phenomenon An abrupt transition, seen in some materials, from elastic deformation

to plastic ﬂow.

Yield strength A stress value obtained graphically that describes no more than a speciﬁed

amount of deformation (usually 0.002). Also known as o¤set yield strength.

Young’s modulus The slope of the elastic part of the stress-strain curve in the elastic region,

same as modulus of elasticity. In some thermoplastic polymers, the Young’s modulus depends on

the level of stress.

PROBLEMS

Section 6-1 Technological Significance

Section 6-2 Terminology for Mechanical

Properties

Section 6-3 The Tensile Test: Use of the Stress-

Strain Diagram

6-1 Draw qualitative engineering stress-engineering

strain curves for a ductile polymer, a ductile metal,

a ceramic, a glass, and natural rubber. Label care-

fully. Rationalize your sketch for each material.

6-2 Why do some polymers get stronger as we stretch

them beyond a region where necking occurs?

6-3 A 3780 N force is applied to a 0.375-cm-diameter

nickel wire having a yield strength of 310 MPa and

a tensile strength of 379 MPa. Determine

(a) whether the wire will plastically deform; and

(b) whether the wire will experience necking.

Problems 183

6-4 A force of 100,000 N is applied to a 10 mm 

20 mm iron bar having a yield strength of 400

MPa and a tensile strength of 480 MPa. Determine

(a) whether the bar will plastically deform; and

(b) whether the bar will experience necking.

6-5 Calculate the maximum force that a 0.5-cm-

diameter rod of Al

, having a yield strength of

241 MPa, can withstand with no plastic de-

formation. Express your answer in Newtons.

6-6 A force of 20,000 N will cause a 1 cm  1 cm bar

of magnesium to stretch from 10 cm to 10.045 cm.

Calculate the modulus of elasticity.

6-7 A polymer bar’s dimensions are 2.5 cm  5cm

37.5 cm. The polymer has a modulus of elasticity

of 4137 MPa. What force is required to stretch

the bar elastically to 38.13 cm?

6-8 An aluminum plate 0.5 cm thick is to withstand a

force of 50,000 N with no permanent deforma-

tion. If the aluminum has a yield strength of 125

MPa, what is the minimum width of the plate?

6-9 A 7.5-cm-diameter rod of copper is to be reduced

to a 5-cm-diameter rod by being pushed through

an opening. To account for the elastic strain,

what should be the diameter of the opening? The

modulus of elasticity for the copper is 117.2  10

MPa and the yield strength is 276 MPa. A 0.15-

cm-thick, 8-cm-wide sheet of magnesium that is

originally 5 m long is to be stretched to a ﬁnal

length of 6.2 m. What should be the length of the

sheet before the applied stress is released? The

modulus of elasticity of magnesium is 45 GPa and

the yield strength is 200 MPa.

6-10 A steel cable 3.13 cm in diameter and 1500 cm

long is to lift a 18,140 kg load. What is the length

of the cable during lifting? The modulus of elas-

ticity of the steel is 207  10

MPa.

Section 6-4 Properties Obtained from the

Tensile Test

and

Section 6-5 True Stress and True Strain

6-11 Deﬁne ‘‘true stress’’ and ‘‘true strain.’’ Compare

with engineering stress and engineering strain.

6-12 Write down the formulas for calculating the

stress and strain for a sample subjected to a ten-

sile test. Assume the sample shows necking.

6-13 The following data were collected from a stand-

ard 1.263-cm-diameter test specimen of a copper

alloy (initial length ðl

Þ¼5 cm):

Load Dl

(N) (cm)

0 0.00000

13,340 0.00418

26,690 0.00833

33,360 0.01043

40,030 0.0225

46,700 0.1

53,380 0.65

55,160 1.25 (maximum load)

50,710 2.55 (fracture)

After fracture, the total length was 7.535 cm and

the diameter was 0.935 cm. Plot the data and

calculate the 0.2% o¤set yield strength along with

(a) the tensile strength;

(b) the modulus of elasticity;

(d) the % reduction in area;

(e) the engineering stress at fracture;

(f) the true stress at fracture; and

(g) the modulus of resilience.

6-14 The following data were collected from a 1-cm-

diameter test specimen of polyvinyl chloride

¼ 5 cm):

Load Dl

(N) (cm)

0 0.00000

1334 0.01865

2669 0.0374

4003 0.05935

5338 0.08

6672 0.115

7384 0.175 (maximum load)

7117 0.235

6316 0.3 (fracture)

After fracture, the total length was 5.225 cm and

the diameter was 0.983 cm. Plot the data and

calculate

(a) the 0.2% o¤set yield strength;

(b) the tensile strength;

(d) the % elongation;

(e) the % reduction in area;

(f) the engineering stress at fracture;

(g) the true stress at fracture; and

(h) the modulus of resilience.

6-15 The following data were collected from a 12-mm-

diameter test specimen of magnesium (l

30.00 mm):

C HA P T E R 6 Mechanical Properties: Fundamentals and Testing184

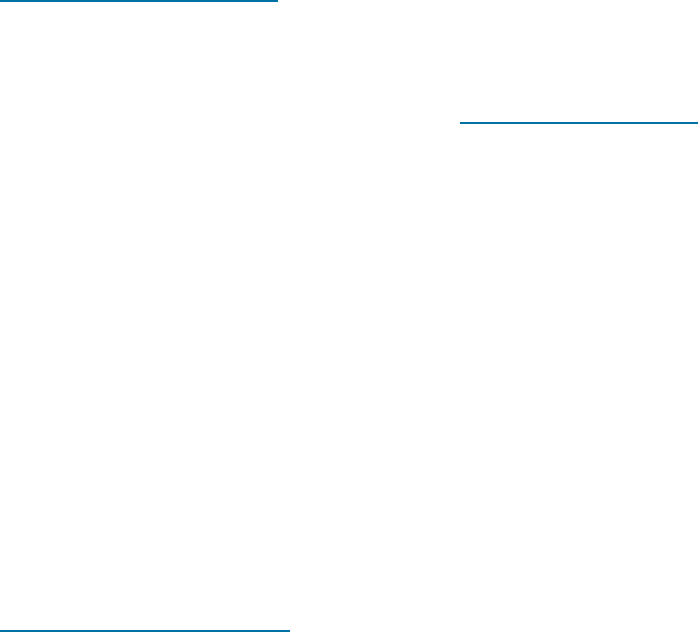
Load Dl

(N ) (mm)

0 0.0000

5,000 0.0296

10,000 0.0592

15,000 0.0888

20,000 0.15

25,000 0.51

26,500 0.90

27,000 1.50 (maximum load)

26,500 2.10

25,000 2.79 (fracture)

After fracture, the total length was 32.61 mm and

the diameter was 11.74 mm. Plot the data and

calculate

(a) the 0.2% o¤set yield strength;

(b) the tensile strength;

(d) the % elongation;

(e) the % reduction in area;

(f) the engineering stress at fracture;

(g) the true stress at fracture; and

(h) the modulus of resilience.

6-16 The following data were collected from a 20-mm-

diameter test specimen of a ductile cast iron

¼ 40.00 mm):

Load Dl

(N ) (mm)

0 0.0000

25,000 0.0185

50,000 0.0370

75,000 0.0555

90,000 0.20

105,000 0.60

120,000 1.56

131,000 4.00 (maximum load)

125,000 7.52 (fracture)

After fracture, the total length was 47.42 mm and

the diameter was 18.35 mm. Plot the data and

calculate

(a) the 0.2% o¤set yield strength;

(b) the tensile strength;

(d) the % elongation;

(e) the % reduction in area;

(f) the engineering stress at fracture;

(g) the true stress at fracture; and

(h) the modulus of resilience.

Section 6-6 The Bend Test for Brittle Materials

6-17 A bar of Al

that is 0.625 cm thick, 1.25 cm

wide, and 22.5 cm long is tested in a three-point

bending apparatus, with the supports located 15 cm

apart. The deﬂection of the center of the bar is

measured as a function of the applied load. The

data are shown below. Determine the ﬂexural

strength and the ﬂexural modulus.

Force Deflection

(N) (cm)

64.5 0.00625

128.5 0.0125

193.0 0.01875

257.5 0.025

382.5 0.03725 (fracture)

6-18 A 1-cm-diameter, 30-cm-long titanium bar has a

yield strength of 345 MPa, a modulus of elasticity

of 110.3  10

MPa, and Poisson’s ratio of 0.30.

Determine the length and diameter of the bar

when a 2224 N load is applied.

6-19 When a tensile load is applied to a 1.5-cm di-

ameter copper bar, the diameter is reduced to

1.498-cm diameter. Determine the applied load,

using the data in Table 6-3.

6-20 A three-point bend test is performed on a block of

ZrO

that is 20 cm long, 1.25 cm wide, and

0.625 cm thick and is resting on two supports 10 cm

apart. When a force of 1780 N is applied, the

specimen deﬂects 0.093 cm and breaks. Calculate

(a) the ﬂexural strength; and

(b) the ﬂexural modulus, assuming that no plas-

tic deformation occurs.

6-21 A three-point bend test is performed on a block

of silicon carbide that is 10 cm long, 1.5 cm wide,

and 0.6 cm thick and is resting on two supports

7.5 cm apart. The sample breaks when a de-

ﬂection of 0.09 mm is recorded. The ﬂexural

modulus for silicon carbide is 480 GPa. Assume

that no plastic deformation occurs. Calculate

(a) the force that caused the fracture; and

(b) the ﬂexural strength.

6-22 A thermosetting polymer containing glass beads

is required to deﬂect 0.5 mm when a force of

500 N is applied. The polymer part is 2 cm wide,

0.5 cm thick, and 10 cm long. If the ﬂexural

modulus is 6.9 GPa, determine the minimum dis-

tance between the supports. Will the polymer

fracture if its ﬂexural strength is 85 MPa? Assume

that no plastic deformation occurs.

6-23 The ﬂexural modulus of alumina is 310.3  10

MPa

and its ﬂexural strength is 317 MPa. A bar of

alumina 0.75 cm thick, 2.5 cm wide, and 25 cm

long is placed on supports 17.5 cm apart. Deter-

mine the amount of deﬂection at the moment the

Problems 185

bar breaks, assuming that no plastic deformation

occurs.

6-24 Ceramics are much stronger in compression than

in tension. Explain why.

Section 6-7 Hardness of Materials

6-25 A Brinell hardness measurement, using a 10-mm-

diameter indenter and a 500-kg load, produces an

indentation of 4.5 mm on an aluminum plate.

Determine the Brinell hardness number (HB) of

the metal.

6-26 When a 3000-kg load is applied to a 10-mm-

diameter ball in a Brinell test of a steel, an in-

dentation of 3.1 mm is produced. Estimate the

tensile strength of the steel.

Section 6-8 Strain Rate Effects and Impact

Behavior

and

Section 6-9 Properties from the Impact Test

6-27 The following data were obtained from a series

of Charpy impact tests performed on four steels,

each having a di¤erent manganese content. Plot

the data and determine

(a) the transition temperature (deﬁned by the

mean of the absorbed energies in the ductile

and brittle regions); and

(b) the transition temperature (deﬁned as the

temperature that provides 50 J of absorbed

energy).

Test Impact Energy (J)

Temperature 0.30% 0.39% 1.01% 1.55%

C MnMnMnMn

100 2 5 5 15

75 2 5 7 25

50 2 12 20 45

25 10 25 40 70

0 305575110

25 60 100 110 135

50 105 125 130 140

75 130 135 135 140

100 130 135 135 140

6-28 Plot the transition temperature versus manganese

content and using the previous data shown dis-

cuss the e¤ect of manganese on the toughness of

steel. What would be the minimum manganese

allowed in the steel if a part is to be used at 0



6-29 The following data were obtained from a series

of Charpy impact tests performed on four ductile

cast irons, each having a di¤erent silicon content.

Plot the data and determine

(a) the transition temperature (deﬁned by the

mean of the absorbed energies in the ductile

and brittle regions); and

(b) the transition temperature (deﬁned as the

temperature that provides 10 J of absorbed

energy).

Plot the transition temperature versus silicon

content and discuss the e¤ect of silicon on the

toughness of the cast iron. What would be the

maximum silicon allowed in the cast iron if a part

is to be used at 25



Test Impact Energy (J)

Temperature 2.55% 2.85% 3.25% 3.63%

C SiSiSiSi

50 2.5 2.5 2 2

5 3 2.5 2 2

0 6 5 3 2.5

25 13 10 7 4

50 17 14 12 8

75 19 16 16 13

100 19 16 16 16

125 19 16 16 16

6-30 FCC metals are often recommended for use at

low temperatures, particularly when any sudden

loading of the part is expected. Explain.

6-31 A steel part can be made by powder metallurgy

(compacting iron powder particles and sintering

to produce a solid) or by machining from a solid

steel block. Which part is expected to have the

higher toughness? Explain.

6-32 What is the di¤erence between a tensile test and

an impact test? Using this, explain why the

toughness values measured using impact tests

may not always correlate with tensile toughness

measured using tensile tests.

6-33 A number of aluminum-silicon alloys have a

structure that includes sharp-edged plates of brit-

tle silicon in the softer, more ductile aluminum

matrix. Would you expect these alloys to be

notch-sensitive in an impact test? Would you ex-

pect these alloys to have good toughness? Explain

your answers.

6-34 What caused NASA’s Challenger 1986 accident?

6-35 How is tensile toughness deﬁned in relation to the

true stress-strain diagram? How is tensile tough-

ness related to impact toughness?

6-36 What factors contributed to the NASA Columbia

2003 accident?

C HA P T E R 6 Mechanical Properties: Fundamentals and Testing186

Fracture Mechanics, Fatigue,

and Creep Behavior

Have You Ever Wondered?

9 Why is it that glass fibers of different lengths have different strengths?

9 Why do some metals and plastics become brittle at low temperatures?

9 Can a material or component ultimately frac ture even if the overall stres s does not exceed the yield

strength?

9 Why do aircrafts have a finite service life?

One goal of this chapter is to introduce the basic

concepts associated with the fracture tough-

ness of materials. In this regard, we will examine

what factors affect the strength of glasses and

ceramics, and how the Weibull distribution

quantitatively describes the variability in their

strength. Another goal is to learn about time-

dependent phenomena such as fatigue, creep,

and stress corrosion. Materials ultimately fail

because of excessive tensile load and/or corro-

sion. This chapter will review some of the basic

testing procedures that engineers use to evalu-

ate many of these properties and the failure of

materials.

187

7-1 Fracture Mechanics

Fracture mechanics is the discipline concerned with the behavior of materials containing

cracks or other small ﬂaws. The term ‘‘ﬂaw’’ refers to such features as small pores

(holes), inclusions, or micro-cracks. The term ‘‘ﬂaw’’ does not refer to atomic level de-

fects such as vacancies, or dislocation s. What we wish to know is the maximum stress

that a material can withstand if it contains ﬂaws of a certain size and geometry. Frac-

ture toughness measures the ability of a material containing a ﬂaw to withstand an ap-

plied load. Note that this does not require a high strain rate (impact).

A typical fracture toughness test may be performed by applying a tensile stress to a

specimen prepared with a ﬂaw of known size and geometry (Figure 7-1). The stress ap-

plied to the material is intensiﬁed at the ﬂaw, which acts as a stress raiser. For a simple

case, the stress intensity factor, K,is

K ¼ f s

ﬃﬃﬃﬃﬃﬃ

ð7-1Þ

where f is a geometry factor for the specimen and ﬂaw, s is the applied stress, and a

is the ﬂaw size (as deﬁned in Figure 7-1). Note that the analytical expression for K

changes with the geometry of the ﬂaw and specimen. If the specimen is assumed to

have an ‘‘inﬁnite’’ width, then f G 1:0. For a small single-edge notch [Figure 7-1(a)],

f ¼ 1:12.

By performing a test on a specimen with a known ﬂaw size, we can determine the

value of K at which a ﬂaw would grow and cause failure. This critical stress intensity

factor is deﬁned as the fracture toughness, K

¼ K required for a crack to propagate ð7-2Þ

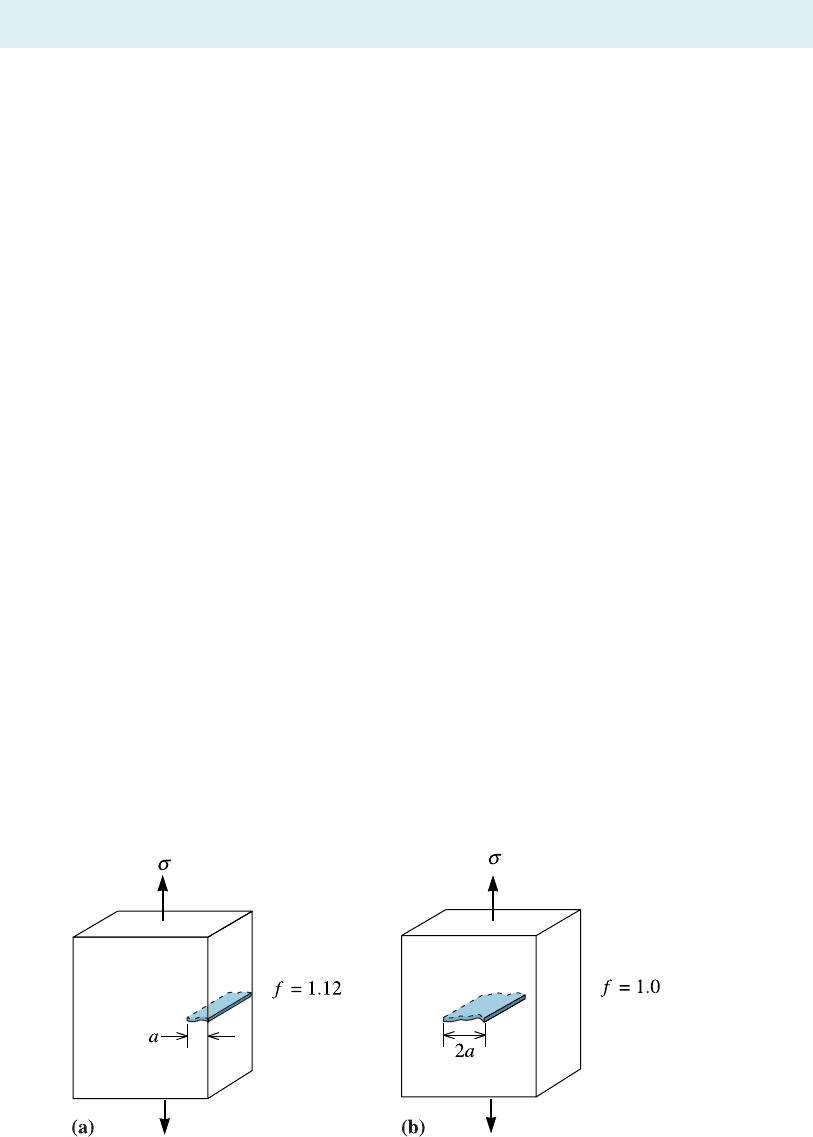
Fracture toughness depends on the thickness of the sample: as thickness increases,

fracture toughness K

decreases to a constant value (Figure 7-2). This constant is called

the plane strain fracture toughness, K

.ItisK

that is normally reported as the prop-

erty of a material. The value of K

does not depend upon the thickness of the sample.

Table 7-1 compares the value of K

to the yield strength of several materials. Units for

fracture toughness are 1:0989 MPa

ﬃﬃﬃﬃﬃﬃ

Figure 7-1 Schematic drawing of fracture toughness specimens with (a) edge and (b) internal

flaws.

C HA P T E R 7 Fracture Mechanics, Fatigue, and Creep Behavior188

The ability of a material to resist the growth of a crack depends on a large number

of factors:

1. Larger ﬂaws reduce the permitted stress. Special manufacturing techniques, such

as ﬁltering impurities from liquid metals and hot pressing or hot isostatic pressing of

powder particles to produce ceramic or superalloy components reduce ﬂaw size and

improve fracture toughness (Chapters 9 and 15).

Figure 7-2

The fracture toughness K

of a

2070 MPa yield strength steel

decreases with increasing thickness,

eventually leveling off at the plane

strain fracture toughness K

TABLE 7-1 9 The plane strain fracture toughness K

of selected materials

Material

Fracture Toughness K

(MPa

ﬃﬃﬃﬃ

)

Yield Strength or

Ultimate Strength (for Brittle Solids)

(MPa)

Al-Cu alloy 24.2 455.1

36.3 324.1

Ti-6% Al-4% V 54.9 896.4

98.9 861.9

Ni-Cr steel 50.3 1641.0

87.9 1420.4

1.8 206.9

4.9 551.6

Transformation toughened ZrO

11.0 413.7

-SiC composite 56.0 827.4

Polymethyl methacrylate polymer 1.0 27.6

Polycarbonate polymer 3.3 57.9

7-1 Fracture Mechanics 189

Askeland D.R., Fulay P.P. Essentials of Materials Science &amp; Engineering

Подождите немного. Документ загружается.

Askeland D.R., Fulay P.P. Essentials of Materials Science & Engineering