Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

This page intentionally left blank

CHAPTER 10

Laplace Transform Methods for

Partial Differential Equations

10.1 Introduction

In many partial differential equation problems that we encounter, such as the diffusion equation

and the wave equation, the time variable is generally understood to have the domain

0 <t<∞. In the case of partial differential equations, the particular operation called the

“Laplace transform” is often used to integrate out the time dependence of the equation, with

the result being a partial differential equation with one fewer independent variable that is

generally easier to solve.

In the case of ordinary differential equations, the operation reduces the differential equation to

an algebraic equation, and, because algebraic equations are generally easier to manipulate and

solve, we see an immediate advantage in the use of the Laplace operation.

10.2 Laplace Transform Operator

We begin by deﬁning the Laplace operator as an integration operation with respect to the time

variable t. With certain restrictions on the function f(t), we deﬁne the Laplace operation or

transform of f(t) to be the integral

F(s) =

∞



f(t) e

−st

We note that the integration operation is performed on the integrand f(t)e

−st

, and the integra-

tion is along the positive real t-axis. The result is a function of the Laplace variable s as indi-

cated by the corresponding capital letter function F(s). The variable s is, in general, a complex

variable. The expression e

−st

is often called the “kernel” of the Laplace transformation.

The preceding integral is an “improper integral,” and in order for this integral to converge, the

restrictions imposed on f(t) are that it be a “piecewise continuous” function of t and of

“exponential order” over the interval I ={t |0 <t<∞}.

640 Chapter 10

By “piecewise continuous” we mean f(t) does not have to be continuous; the interval

I ={t |0 <t<∞} can be divided into a ﬁnite number of subintervals such that the function

f(t) is continuous in the interior of each subinterval and appoaches ﬁnite limits at each end

point of the subinterval. By “exponential order” we mean that there is a positive constant σ

such that the following product remains bounded by some constant M; that is,

−σt

|f(t)| <M

as t goes to inﬁnity. The greatest lower bound on the value of σ is called the “abscissa of

convergence” of f(t).

Some functions and their evaluated Laplace transforms, that may be of immediate use to us in

solving some partial differential equations, are given here:

f 1(t) = e

sin(bt), F 1(s) =

(s −a)

f 2(t) = e

cos(bt), F 2(s) =

s −a

(s −a)

f 3(t) = e

,F3(s) =

(n +1)

(s −a)

n+1

In the preceding integrations, we have assumed that a and b are real and the real part of s is

larger than a, which is larger than σ—that is, Re{s} >a>σ. All of these integrations can be

conﬁrmed by direct integration of the Laplace transform integral.

Because we will be confronting derivatives in our solutions to partial differential equations, we

now consider Laplace transforms of derivatives of functions with respect to the transformed

variable t. By integration by parts, it can be shown that the transform of the ﬁrst derivative

reads

∞





f(t)



−st

dt = sF(s) −f(0)

and the transform of the second derivative reads

∞





f(t)



−st

dt = s

F(s) −sf ( 0) −



f(0)



Laplace Transform Methods for Partial Diff erential Equations 641

where f(0) and

f(0) denote the zero and ﬁrst derivative, respectively, of the function f(t) at

time t = 0. These results are conditional on Re{s} being greater than the abscissa of

convergence of f(t) and its ﬁrst two derivatives.

10.3 Inverse Transform and Convolution Integral

If the function f(t) satisﬁes the conditions of exponential order and piecewise continuity, then

it can be shown that there exists a uniqueness between the function and its inverse. From

complex analysis, it can be shown that we can retrieve the function f(t) from its transform F(s)

by performing the following inverse operation:

f(t) =

a+i∞



a−i∞

F(s) e

2πi

This inverse operation is an integration over the variable s in the complex s-plane along the

line Re{s}=a, where a is any point greater than σ, the “abscissa of convergence” of f(t).We

do not intend to evaluate inverses from integrations in the complex plane here, since this would

take us too far from our immediate intentions.

Generally, inverse transforms are evaluated by doing partial fraction expansions on F(s) and

then relating the expansion terms to previously evaluated transforms. An alternative procedure

is to use a convolution method similar to that developed in Chapter 9.

For Laplace transforms, the convolution integral reads as follows. Let F(s) be the Laplace

transform of f(t) and assume that it can be partitioned into a product of two functions F 1(s)

and F 2(s); that is,

F(s) = F 1(s)F 2(s)

where F 1(s) is the Laplace transform of f 1(t) and F 2(s) is the Laplace transform of f 2(t):

F 1(s) =

∞



f 1(t) e

−st

and

F 2(s) =

∞



f 2(t) e

−st

Of course, f 1(t) and f 2(t) must both be piecewise continuous and of exponential order. It can

be shown (see related references) that f(t), the inversion of F(s), can be expressed as the

convolution integral

f(t) =



f 1(τ)f 2(t −τ) dτ

642 Chapter 10

We take advantage of the convolution integral in evaluating some inverses in some of the

following problems.

10.4 Laplace Transform Procedures on the Diffusion

Equation

We ﬁrst consider the nonhomogeneous partial differential equation for diffusion in one spatial

dimension in rectangular coordinates as given here:

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



+h(x, t)

with the initial condition

u(x, 0) = f(x)

where h(x, t) accounts for any internal source terms in the system.

In evaluating the Laplace transform of terms in the given partial differential equation, we have

to contend with taking improper integrals, with respect to t, of functions that are dependent on

both x and t. We denote the Laplace transform of u(x, t) with respect to the time variable t by

the capital letter representation shown here:

U(x, s) =

∞



u(x, t) e

−st

Proceeding formally with the evaluation of transforms of the derivative terms in the given

partial differential equation, we get

∞





∂

∂t

u(x, t)



−st

dt = sU(x, s) −u(x, 0)

where U(x, s) denotes the Laplace transform of u(x, t) with respect to t, and u(x, 0) denotes the

initial value of u(x, t).

Proceeding formally in evaluating the transforms of the partial derivative terms with respect to

the spatial variable x,weget

∞





∂

∂x

u(x, t)



−st

dt =

∂

∂x

U(x, s)

This operation suggests that we could interchange the differentiation operation, with respect to

x, with the integration operation, with respect to t. The conditions for the validity of doing this

Laplace Transform Methods for Partial Diff erential Equations 643

are based on the uniform convergence of the improper integrals of the derivative terms.

Assuming the validity of these operations, the Laplace transform, with respect to t,ofthe

given partial differential equation yields

∂

∂x

U(x, s) −

sU(x, s)

=−

f(x)

−

H(x, s)

Here, H(x, s) is the Laplace transform of the source term; that is,

H(x, s) =

∞



h(x, t) e

−st

The preceding differential equation is an ordinary second-order nonhomogeneous differential

equation in the single spatial variable x. We investigated the solutions for this equation in

Chapter 1. The solutions are, of course, dependent on the spatial boundary conditions on the

problem.

The preceding operations demonstrate the advantage of using the Laplace transform operation

on the original partial differential equation. The time dependence of the partial differential

equation has been integrated out, and the result is a lower-order differential equation in the

single variable x.

We now consider the application of the Laplace transform to evaluate some solutions to the

heat equation over semi-inﬁnite domains with respect to the spatial variable x. We focus on

those types of problems that have nonhomogeneous boundary conditions. These are problems

that cannot ordinarily be solved using the Fourier transform methods as covered in Chapter 9.

Further, we do not consider using Laplace transform methods for diffusion problems over ﬁnite

domains here, since eigenfunction expansion methods, as used in Chapters 3, 6, and 8, are

more effective.

In general, we consider time-dependent boundary conditions that are nonhomogeneous at

x = 0 and that are bounded at x =∞; that is,

u(0,t)+κ

(0,t)= q(t)

and

u(∞,t)<∞

The transform of these boundary conditions gives us

U(0,s)+κ



∂

∂x

U(0,s)



= Q(s)

and

U(∞,s)<∞

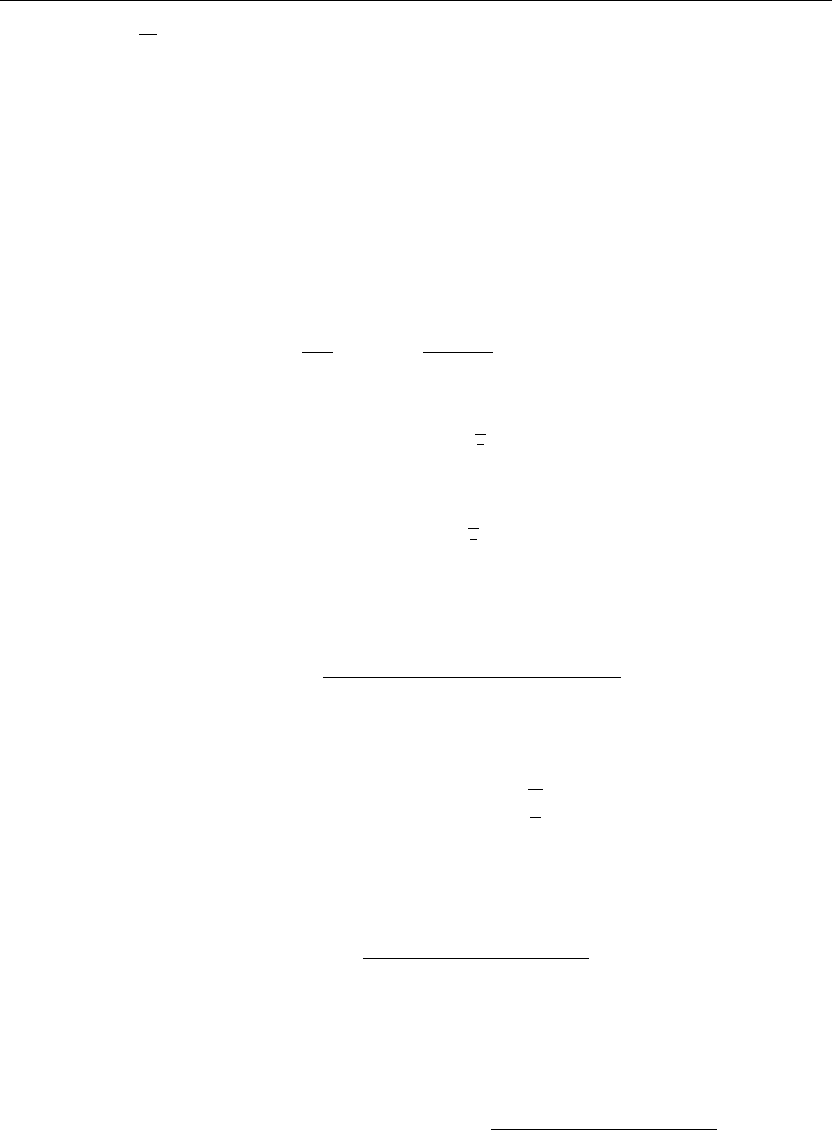
644 Chapter 10

where the term

∂

∂x

U(0,s)is understood to be the x-dependent derivative of U(x, s) evaluated at

x = 0 and Q(s) is the Laplace transform of q(t) as shown here:

Q(s) =

∞



q(t) e

−st

The earlier differential equation is a nonhomogeneous ordinary differential equation with

respect to the spatial variable x. We solved similar problems in Chapter 1. To develop a general

solution, we must ﬁrst consider ﬁnding a set of basis vectors for the corresponding

homogeneous differential equation:

∂

∂x

U(x, s) −

sU(x, s)

= 0

Two basis vectors are

(x, s) = e

−

√

and

(x, s) = e

√

From the two basis vectors, as shown in Section 1.7, we are able to generate the second-order

Green’s function G(x, v, s):

G(x, v, s) =

(v, s)φ

(x, s) −φ

(x, s)φ

(v, s)

(

(v, s), φ

(v, s)

)

where the denominator term is the familiar Wronskian, which, for the just given basis vectors,

is evaluated to be

W(φ

(v, s), φ

(v, s)) = 2



Thus, from the method of variation of parameters, the particular solution to the

nonhomogeneous ordinary differential equation in x is

Up(x, s) =−





G(x, v, s)(f(v) +H(v, s))



The general solution to the x-dependent differential equation is the sum of the complementary

solution and the preceding particular solution. Combining the two solutions, we get the general

solution for the transform U(x, s):

U(x, s) = C1(s)φ

(x, s) +C2(s)φ

(x, s) −





G(x, v, s)(f(v) +H(v, s))



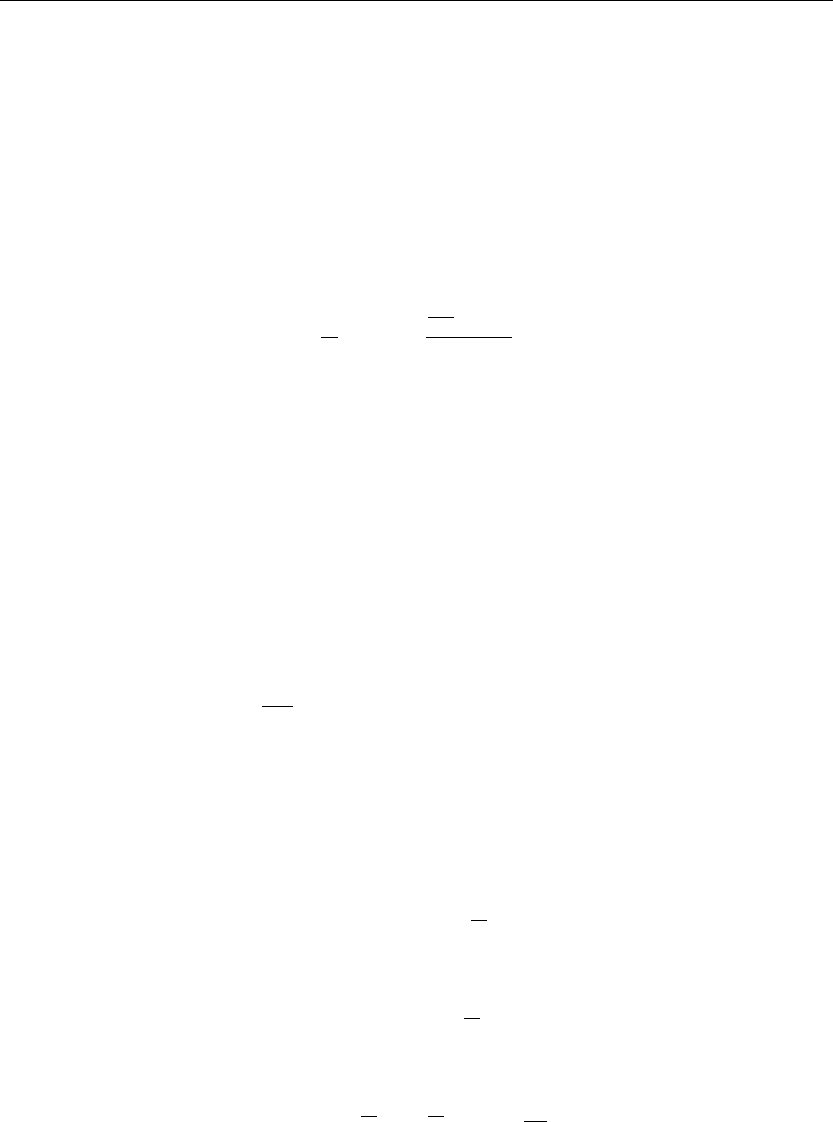
Laplace Transform Methods for Partial Diff erential Equations 645

The arbitrary coefﬁcients C1(s) and C2(s) are to be determined from the boundary conditions

for the problem. The ﬁnal solution to our problem is the inverse Laplace transform of U(x, s).

We demonstrate these concepts discussed by solving an illustrative problem.

DEMONSTRATION: We seek the temperature distribution u(x, t) in a thin rod over the

semi-inﬁnite interval I ={x |0 <x<∞} whose lateral surface is insulated. The left end of the

rod is held at the temperature 0, and the rod has the initial temperature distribution f(x) given

following. There is no internal heat source in the system, and the diffusivity is k = 1/5.

SOLUTION: The diffusion partial differential equation is

∂

∂t

u(x, t) =

∂

∂x

u(x, t)

Because the left end of the rod is held at the ﬁxed temperature 0, we have a type 1 condition at

x = 0. Further, we require the solution to be ﬁnite at inﬁnity; thus, the boundary conditions are

u(0,t)= 0 and u(∞,t)<∞

The rod has an initial temperature distribution u(x, 0) = f(x) given as

f(x) = sin(x)

We begin by taking the Laplace transform, with respect to the variable t, of the partial

differential equation. This yields the ordinary differential equation in the spatial variable x:

∂

∂x

U(x, s) −5sU(x, s) =−5 sin(x)

We solve this nonhomogeneous ordinary differential equation, in the variable x, subject to the

transformed boundary conditions

U(0,s)= 0 and U(∞,s)<∞

From Section 1.4, a set of basis vectors is

(x, s) = e

−

√

5sx

and

(x, s) = e

√

5sx

The Wronskian of this basis is evaluated to be



−

√

5sv

, e

√

5sv



= 2

√

5 s

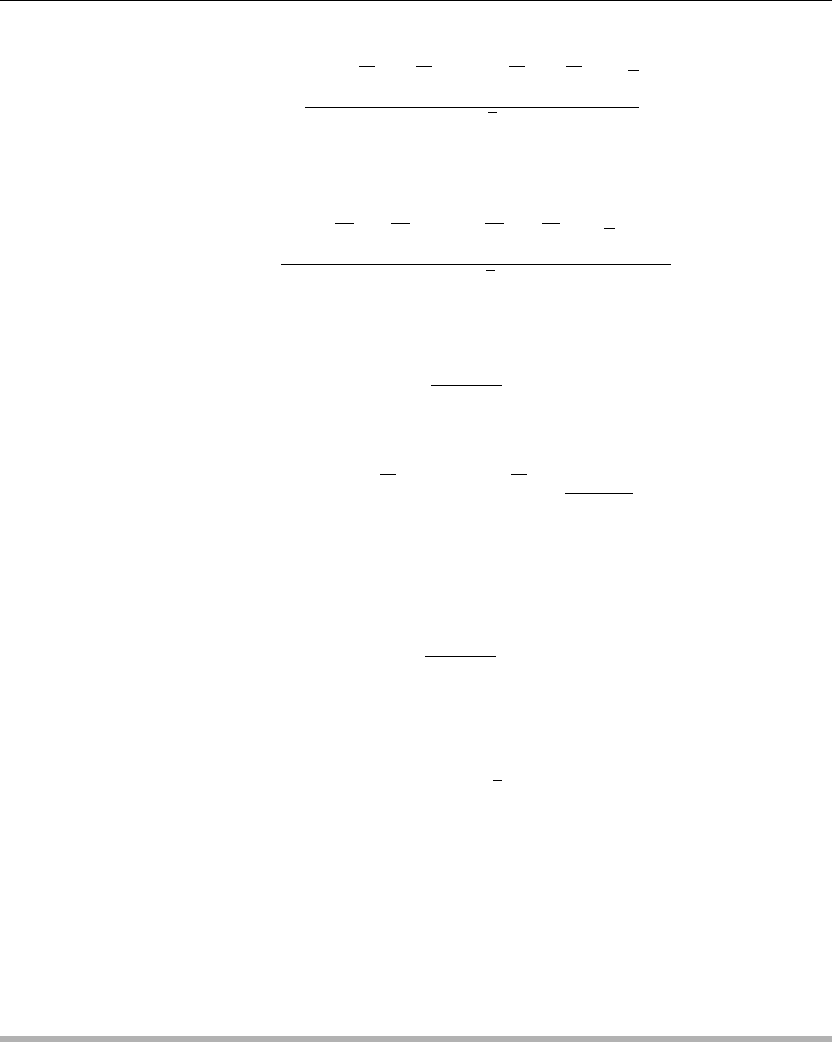
646 Chapter 10

and the corresponding Green’s function is

G(x, v, s) =



−

√

5sv

√

5sx

− e

−

√

5sx

√

5sv



√

By the method of variation of parameters, from Section 1.7, the particular solution to the

preceding differential equation can be expressed in terms of the Green’s function as the integral

Up(x, s) =−

⎛

⎝





−

√

5sv

√

5sx

− e

−

√

5sx

√

5sv



√

5 sin(v)

√

⎞

⎠

which is evaluated to be

Up(x, s) =

5 sin(x)

5 s +1

Thus, the general solution to the transformed equation is

U(x, s) = C1(s) e

−

√

5sx

+C2(s) e

√

5sx

5 sin(x)

5s +1

where C1(s) and C2(s) are arbitrary constants. Substituting the boundary condition at x = 0

and requiring the solution to be ﬁnite as x approaches inﬁnity, for Re{s} > 0, we determine that

C1(s) = 0 and C2(s) = 0, and we arrive at the ﬁnal transformed solution:

U(x, s) =

5 sin(x)

5s +1

The ﬁnal solution for the spatial- and time-dependent temperature of the system is evaluated

from the inverse Laplace transform of the preceding, and this yields

u(x, t) = sin(x) e

−

(10.1)

The details for the development of the solution and the graphics are given later in one of the

Maple worksheet examples. Note that this problem could not be solved by using the Fourier

integral with respect to the variable x as we did in Chapter 9. The reason for this is that the

initial function f(x) is not absolutely integrable over the given interval I.

10.5 Example Laplace Transform Problems for the

Diffusion Equation

We now look at some speciﬁc applications of the Laplace transform to evaluate solutions to the

heat equation over semi-inﬁnite intervals with respect to the spatial variable x. We focus on

those types of problems that have nonhomogeneous boundary conditions—problems that

cannot ordinarily be solved using Fourier transform methods as covered in Chapter 9.

Laplace Transform Methods for Partial Diff erential Equations 647

EXAMPLE 10.5.1: We seek the temperature distribution u(x, t) in a thin rod over the

semi-inﬁnite interval I ={x |0 <x<∞} whose lateral surface is insulated. The left end of the

rod is held at a ﬁxed temperature given following, and the rod has an initial temperature

distribution equal to 0. There is no internal heat source in the system and the thermal

diffusivity is k = 1/10. We solve by taking Laplace transforms with respect to t.

SOLUTION: The diffusion partial differential equation is

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



The boundary conditions are

u(0,t)= 10 and u(∞,t)<∞

The initial condition is

u(x, 0) = 0

The Laplace transformed equation reads

∂

∂x

U(x, s) −

sU(x, s)

=−

f(x)

Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary

conditions are

U(0,s)= Q(s) and U(∞,s)<∞

Assignment of system parameters

> restart:with(plots):with(inttrans):k:=1/10:q(t):=10:f(x):=0:

Transformed equation in x reads

> diff(U(x,s),x,x)−(1/k)*s*U(x,s)=−1/k*f(x);

∂

∂x

U(x, s) −10 sU(x, s) = 0 (10.2)

Transformed boundary conditions

> Q(s):=Int(q(t)*exp(−s*t),t=0..inﬁnity);

Q(s) :=

∞



10 e

−st

dt (10.3)