Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


608 Chapter 9
and
d
2
dx
2
X(x) −λX(x) = 0
A set of basis vectors for the y equation for λ>0 is, from Chapter 1,
y1(y) = e
i
√
λy
and
y2(y) = e
−i
√
λy
If we set λ = ω
2
, then we satisfy the condition that the y-dependent portion of the solution be
bounded as y goes to plus or minus infinity. Thus, the y-dependent orthonormalized singular
eigenfunctions, as shown in Section 9.2, can be written as
√
2e
iωy
2
√
π
for −∞ <ω<∞.
From the Fourier integral theorem, the singular eigenfunctions are “complete” with respect to
piecewise smooth and absolutely integrable functions over the infinite domain. Thus, we can
write our solution as the superposition of the singular eigenfunctions just given, or,
equivalently, as the Fourier integral
u(x, y) =
∞
−∞
U(ω, x) e
iωy
2π
dω
From Section 9.2, U(ω, x) is the Fourier transform of u(x, y) with respect to the variable y.
If we substitute the assumed solution into the preceding partial differential equation, and we
assume validity of the formal interchange between the differentiation and the integration
operators, then we get the following differential equation in x:
∂
2
∂x
2
U(ω, x) −ω
2
U(ω, x) = 0
From Chapter 1, a set of basis vectors for the preceding corresponding homogeneous
differential equation is
x1(x) = e
ωx
and
x2(x) = e
−ωx

Infinite and Semi-infinite Spatial Domains 609
The solution to the differential equation in x is
U(ω, x) = A(ω) e
ωx
+B(ω) e
−ωx
Thus, taking the inverse transform, the solution to our homogeneous partial differential
equation can be written as the Fourier integral
u(x, y) =
∞
−∞
A(ω) e
ωx
+B(ω) e
−ωx
e
iωy
2π
dω
The Fourier coefficients A(ω) and B(ω) are determined from the boundary conditions imposed
on the problem.
If the domain is semi-infinite in extent with respect to either the x or y variable, then depending
on the homogeneous boundary conditions imposed at the origin, we write our solution as either
a Fourier sine or Fourier cosine integral, and we proceed as we did in Sections 9.6 and 9.8; the
method of images is also available for use for semi-infinite intervals.
In Section 9.5, we discussed the convolution method in solving diffusion equation problems,
and we provided several examples using this method. This method can also be used to solve
Laplace equation problems. We now demonstrate the convolution method of solution for an
illustrative problem.
DEMONSTRATION: We seek the electrostatic potential distribution u(x, y) in a charge-free
region over the two-dimensional domain (the right half-plane) D ={(x, y) |0 <x<∞,
−∞ <y<∞}. The edge x = 0 has a potential distribution f(y) given as follows.
SOLUTION: The Laplace partial differential equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The domain is infinite in extent with respect to the y variable and semi-infinite in extent with
respect to the x variable. We require the solution to be absolutely integrable over this infinite
half-plane. In addition, there is a given potential distribution along the line x = 0. Thus, the
boundary conditions on the problem are
u(0,y)= f(y) and
∞
−∞
∞
0
|u(x, y)|dx dy<∞
Because we have a nonhomogeneous boundary condition with respect to x at the line x = 0,
and the boundary with respect to y is infinite in extent, then we write the solution u(x, y) as a

610 Chapter 9
Fourier integral with respect to the y variable—that is,
u(x, y) =
∞
−∞
U(ω, x) e
iωy
2π
dω
Substitution of this solution into the Laplace partial differential equation yields the ordinary
differential equation in x:
∂
2
∂x
2
U(ω, x) −ω
2
U(ω, x) = 0
From knowledge of the two basis vectors (see Section 1.4), the general solution of this
homogeneous differential equation for the Fourier transform of the solution is
U(ω, x) = A(ω) e
ωx
+B(ω) e
−ωx
Because the solution must remain bounded as x goes to infinity, and since ω takes on both
positive and negative values, we set
U(ω, x) = C(ω) e
−
|
ω
|
x
where C(ω) is an unknown arbitrary function of ω.
With knowledge of the given Fourier transform, the Fourier integral of the solution reads
u(x, y) =
∞
−∞
C(ω) e
−
|
ω
|
x
e
iωy
2π
dω
Substitution of the boundary condition u(0,y)= f(y) at x = 0 yields
f(y) =
∞
−∞
C(ω) e
iωy
2π
dω
Thus, C(ω) is the Fourier transform of f(y)—that is,
C(ω) =
∞
−∞
f(y) e
−iωy
dy
We can combine the two given integrals, as we did in Section 9.5 for the diffusion equation,
and our solution becomes
u(x, y) =
∞
−∞
⎛
⎝
∞
−∞
f(ζ) e
−iωζ
2π
dζ
⎞
⎠
e
−
|
ω
|
x
e
iωy
dω

Infinite and Semi-infinite Spatial Domains 611
If we assume validity of the formal interchange of the order of integration, we get
u(x, y) =
∞
−∞
f(ζ)
⎛
⎝
∞
−∞
e
−
|
ω
|
x
e
iω(y−ζ)
2π
dω
⎞
⎠
dζ
The interior integral is the Fourier integral, with respect to the variable v = y −ζ,ofthe
function
g(x, y −ζ) =
x
π
x
2
+(y −ζ)
2
Thus, our solution can be written as the convolution integral
u(x, y) =
∞
−∞
f(ζ)g(x, y −ζ) dζ
From knowledge of the boundary function u(0,y)= f(y), we can evaluate the final solution.
We now provide an illustrative example where the given potential distribution along the x = 0
line is u(x, 0) = f(y), where
f(y) = H(y +1) −H(y −1)
From the definition of the Heaviside functions, this corresponds to a potential on the y-axis,
which has a value of 1 for |y| < 1 and 0 for |y| > 1. For this special case of potential
distribution along the y-axis, our integral solution above becomes
u(x, y) =
∞
−∞
(
H(ζ +1) −H(ζ −1)
)
x
x
2
+(y −ζ)
2
π
dζ
This integral is reduced to the equivalent integral
u(x, y) =
1
−1
x
x
2
+(y −ζ)
2
π
dζ
Evaluation of this integral yields the electrostatic potential distribution
u(x, y) =
−arctan
y−1
x
+arctan
y+1
x
π
The details for the development of this solution along with the graphics are given later in one
of the Maple worksheet examples.

612 Chapter 9
9.12 Example Laplace Equation over Infinite and
Semi-infinite Domains
We now consider some Laplace equation problems over both infinite and semi-infinite domains.
EXAMPLE 9.12.1: (Temperature distribution along an infinite strip) We seek the steady-state
temperature distribution u(x, y) in a thin plate over the domain D ={(x, y) |−∞<x<∞,
0 <y<1} whose lateral surfaces are insulated. The edge y = 0 is at a fixed temperature of 0,
and the edge y = 1 has the temperature distribution f(x) given as follows.
SOLUTION: The homogeneous Laplace equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The boundary conditions are
∞
0
∞
−∞
|u(x, y)|dx dy<∞
and
u(x, 0) = 0 and u(x, 1) =
1
1 +x
2
Since the domain is infinite in extent with respect to the x variable, we write the Fourier
integral solution with respect to the x variable as
u(x, y) =
∞
−∞
U(ω, y) e
iωx
2π
dω
where the Fourier transform U(ω, y) satisfies the y-dependent differential equation
∂
2
∂y
2
U(ω, y) −ω
2
U(ω, y) = 0
Assignment of system parameters
> restart:with(inttrans):with(plots):b:=1:f(x):=1/(1+xˆ2):
Solution to the y-dependent equation
> U(omega,y):=A(omega)*cosh(omega*y)+B(omega)*sinh(omega*y);
U(ω, y) := A(ω) cosh(ωy) +B(ω) sinh(ωy) (9.71)
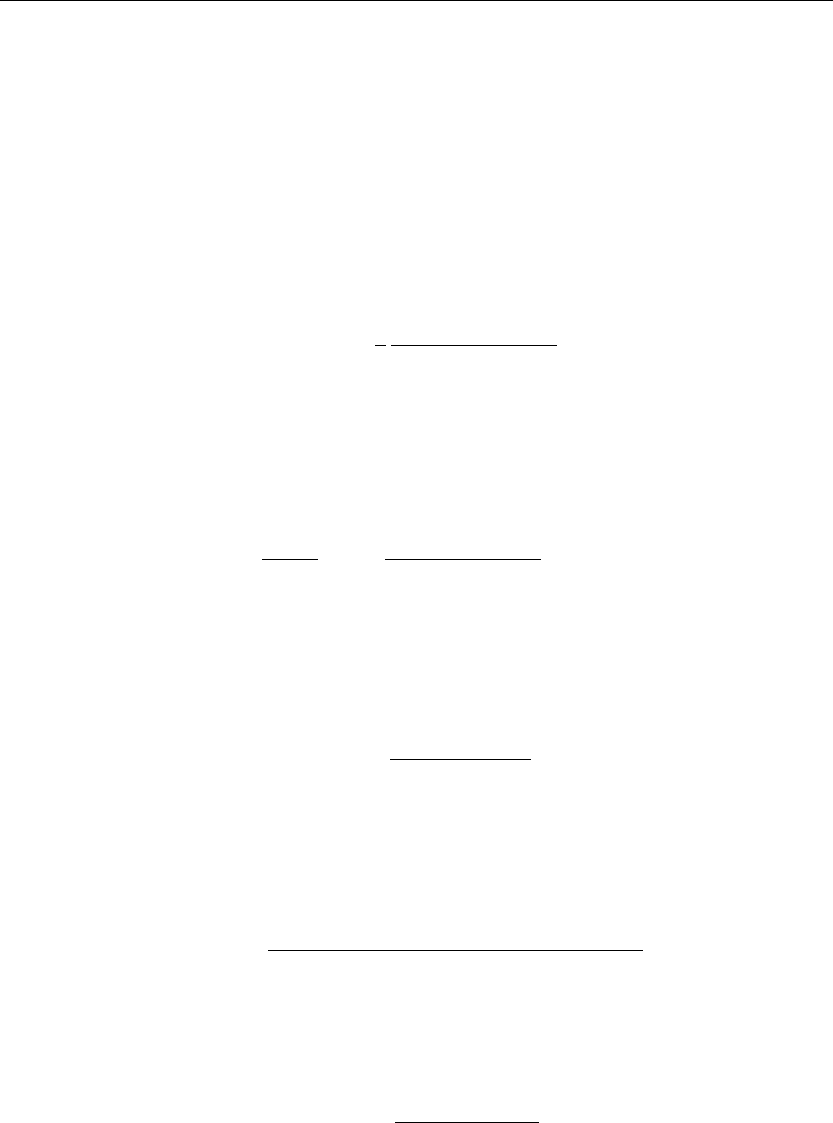
Infinite and Semi-infinite Spatial Domains 613
Substitution of the boundary condition at y = 0 gives A(ω) = 0 and
> U(omega,y):=B(omega)*sinh(omega*y);
U(ω, y) := B(ω) sinh(ωy) (9.72)
Fourier integral solution
> u(x,y):=Int(B(omega)*sinh(omega*y)*(1/(2*Pi))*exp(I*omega*x),omega=
−infinity..infinity);
u(x, y) :=
∞
−∞
1
2
B(ω) sinh(ωy) e
Iωx
π
dω (9.73)
Substituting the boundary condition u(x, 1) = f(x) at y = 1 yields
> f(x)=subs(y=b,u(x,y));
1
1 +x
2
=
∞
−∞
B(ω) sinh(ω) e
Iωx
π
dω (9.74)
The coefficient B(ω) is found from the Fourier transform
> B(omega):=Int(f(x)*(1/sinh(omega*b))*exp(−I*omega*x),x=−infinity..infinity);
B(ω) :=
∞
−∞
e
−Iωx
1 +x
2
sinh(ω)
dx (9.75)
Evaluation of this integral yields
> B(omega):=factor(fourier(f(x)/sinh(omega*b),x,omega));
B(ω) :=
π
e
ω
Heaviside(−ω) + e
−ω
Heaviside(ω)
sinh(ω)
(9.76)
Solution for U(ω, y)
> U(omega,y):=Pi*exp(−abs(omega))*sinh(omega*y)/sinh(omega);
U(ω, y) :=
π e
−|ω|
sinh(ωy)
sinh(ω)
(9.77)
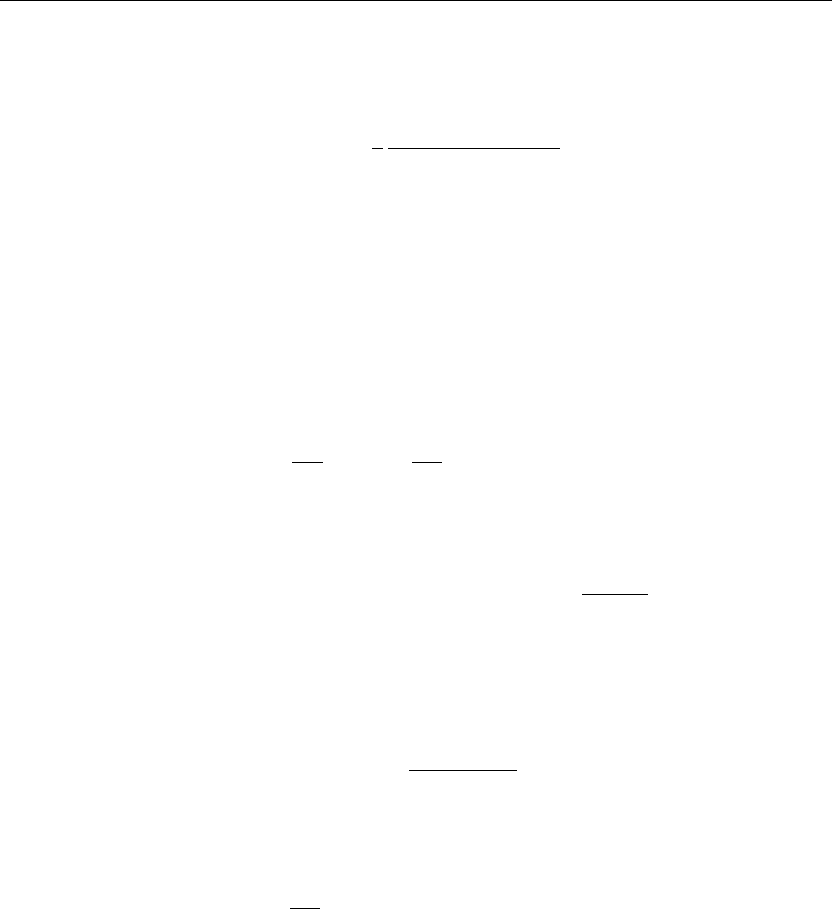
614 Chapter 9
Fourier integral solution
> u(x,y):=int(U(omega,y)*(1/(2*Pi))*exp(I*omega*x),omega=−infinity..infinity);
u(x, y) :=
∞
−∞
1
2
e
−|ω|
sinh(ωy) e
Iωx
sinh(ω)
dω (9.78)
We leave our answer in integral form.
EXAMPLE 9.12.2: (Steady-state temperature in upper half of plane) We seek the steady-state
temperature distribution u(x, y) in a thin plate over the domain D ={(x, y) |−∞<x<∞,
0 <y<∞} whose lateral surfaces are insulated. The edge y = 0 has a temperature distribution
f(x) given as follows.
SOLUTION: The homogeneous Laplace equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The boundary conditions are
∞
0
∞
−∞
|u(x, y)|dx dy<∞ and u(x, 0) =
16
16 +x
2
Because the domain is infinite in extent with respect to the x variable, we write the Fourier
integral solution with respect to the x variable as
u(x, y) =
∞
−∞
U(ω, y) e
iωx
2π
dω
where the Fourier transform U(ω, y) satisfies the y-dependent differential equation
∂
2
∂y
2
U(ω, y) −ω
2
U(ω, y) = 0
Assignment of system parameters
> restart:with(inttrans):with(plots):f(x):=16/(16+xˆ2):
Solution to the y-dependent equation
> U(omega,y):=A(omega)*exp(omega*y)+B(omega)*exp(−omega*y);assume(y>0):
U(ω, y) := A(ω) e
ωy
+B(ω) e
−ωy
(9.79)

Infinite and Semi-infinite Spatial Domains 615
Because the solution must remain bounded as y goes to plus or minus infinity, and because ω
takes on positive and negative values, we set
> U(omega,y):=C(omega)*exp(−abs(omega)*y);
U(ω, y∼) := C(ω) e
−|ω|y∼
(9.80)
Fourier integral solution
> u(x,y):=Int(U(omega,y)/(2*Pi)*exp(I*omega*x),omega=−infinity..infinity);
u(x, y ∼) :=
∞
−∞
1
2
C(ω) e
−|ω|y ∼
e
Iωx
π
dω (9.81)
Substituting the boundary condition u(x, 0) = f(x) at y = 0 yields
> f(x)=eval(subs(y=0,u(x,y)));
16
16 +x
2
=
∞
−∞
1
2
C(ω) e
Iωx
π
dω (9.82)
Thus, the coefficient C(ω) is found from the Fourier transform
> C(omega):=Int(f(x)*exp(−I*omega*x),x=−infinity..infinity);
C(ω) :=
∞
−∞
16 e
−Iωx
16 +x
2
dx (9.83)
Evaluation of this integral using the Maple fourier command yields
> C(omega):=fourier(f(x),x,omega);
C(ω) := 4π
e
4ω
Heaviside(−ω) + e
−4ω
Heaviside(ω)
(9.84)
Solution for U(ω, y)
> U(omega,y):=C(omega)*exp(−abs(omega)*y);
U(ω, y∼) := 4π
e
4ω
Heaviside(−ω) + e
−4ω
Heaviside(ω)
e
−|ω|y ∼
(9.85)
Fourier integral solution
> u(x,y):=Int(U(omega,y)*(1/(2*Pi))*exp(I*omega*x),omega=−infinity..infinity);
u(x, y ∼) :=
∞
−∞
2
e
4ω
Heaviside(−ω) + e
−4ω
Heaviside(ω)
e
−|ω|y ∼
e
Iωx
dω (9.86)
616 Chapter 9
Partitioning the integral over positive and negative values of ω yields
> u(x,y):=int(U(omega,y)*(1/(2*Pi))*exp(I*omega*x),omega=−infinity..0)+int(U(omega,y)*
(1/(2*Pi))*exp(I*omega*x),omega=0..infinity):
> u(x,y):=simplify(evalc(value(%)));
u(x, y ∼) :=
4(4 +y ∼)
16 +8y ∼+y∼
2
+x
2
(9.87)
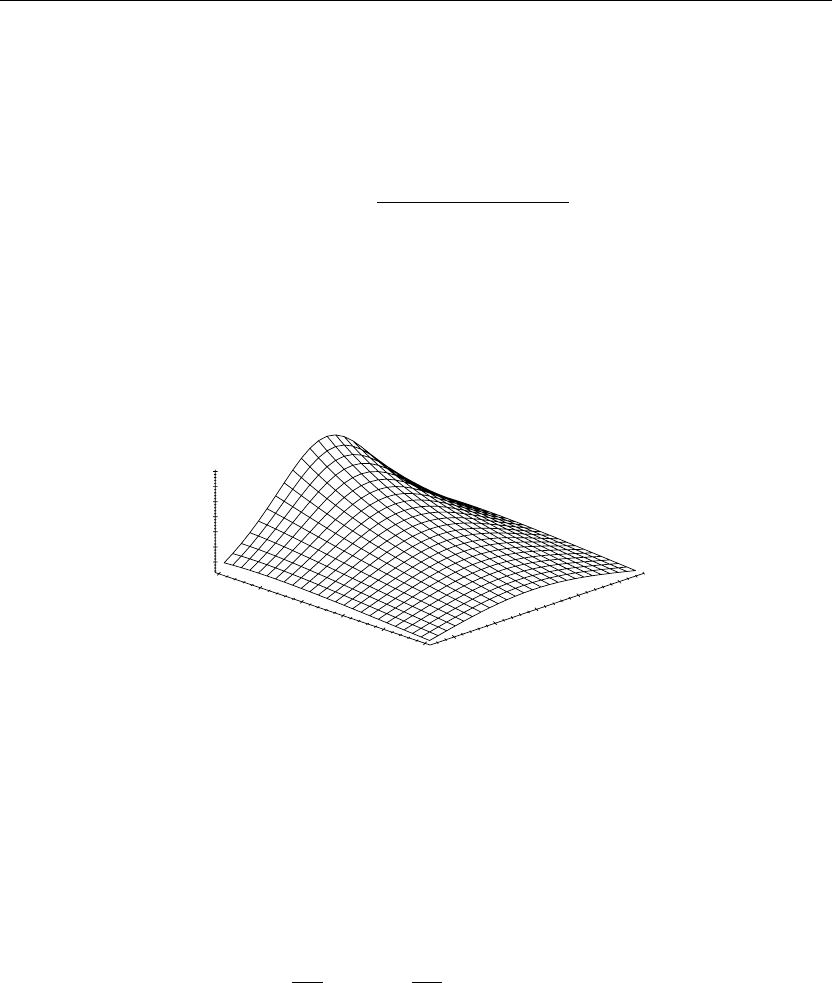
> plot3d(u(x,y),x=−5..5,y=0..5,axes=framed,thickness=1);
The three-dimensional surface shown in Figure 9.9 illustrates the steady-state temperature
distribution u(x, y) in the plate. The temperature isotherms are obtained by clicking on the
graph and choosing the “Render the plot using the polygon patch and contour style” option and
then clicking the “redraw” button in the graphics bar.
0.8
0.7
0.6
0.5
0.4
0.9
1
0
2
2
22
24
0
3
4
5
4
x
1
y~
Figure 9.9
EXAMPLE 9.12.3: (Electrostatic potential solved by convolution) We seek the electrostatic
potential distribution u(x, y) in a charge-free region over the domain D ={(x, y) |
0 <x<∞, −∞ <y<∞}. The edge x = 0 has a potential distribution f(y) given as follows.
Since the domain is infinite in extent with respect to y, we use a Fourier integral solution in y
along with a convolution.
SOLUTION: The homogeneous Laplace equation is
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
The boundary conditions are
∞
−∞
∞
0
|u(x, y)|dx dy<∞ and u(0,y)= H(y +1) −H(y −1)

Infinite and Semi-infinite Spatial Domains 617
From the definition of the Heaviside function, this potential distribution corresponds to a
potential of magnitude 1 at x = 0 along the y-axis for |y| < 1 and 0 for 1 < |y|.
Because the domain is infinite in extent with respect to the y variable, we write the Fourier
integral solution with respect to the y variable as
u(x, y) =
∞
−∞
U(ω, x) e
iωy
2π
dω
where the Fourier transform U(ω, x) satisfies the x-dependent differential equation
∂
2
∂x
2
U(ω, x) −ω
2
U(ω, x) = 0
Assignment of system parameters
> restart:with(inttrans):with(plots):
Solution to the x-dependent equation
> U(omega,x):=A(omega)*exp(omega*x)+B(omega)*exp(−omega*x);
U(ω, x) := A(ω) e
ωx
+B(ω) e
−ωx
(9.88)
Because the solution must remain bounded as x goes to infinity, and because ω takes on
positive and negative values, we set
> U(omega,x):=C(omega)*exp(−abs(omega)*x);
U(ω, x) := C(ω) e
−|ω|x
(9.89)
Fourier integral solution
> u(x,y):=Int(U(omega,x)*(1/(2*Pi))*exp(I*omega*y),omega=−infinity..infinity);
u(x, y) :=
∞
−∞
1
2
C(ω) e
−|ω|x
e
Iωy
π
dω (9.90)
Substituting the boundary condition u(0,y)= f(y) at x = 0 yields
> f(y)=eval(subs(x=0,u(x,y)));
f(y) =
∞
−∞
1
2
C(ω) e
Iωy
π
dω (9.91)
