Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


628 Chapter 9
Heat source:
h(x, t) = e
−
x
2
4
sin(t)
9.23. Consider a thin rod whose lateral surface is insulated over the infinite interval
I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).
There is a heat source term h(x, t) (dimension of degrees per second) in the system, and
the diffusivity is k = 1/4. Evaluate the temperature distribution u(x, t) in the form of a
Fourier integral. If possible, evaluate the inverse by using either the inverse command
or a convolution integral.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial condition:
f(x) = 0
Heat source:
h(x, t) = x e
−
x
2
4
cos(t)
Fourier Integral Solutions for the Wave Equation
We now consider transverse wave propagation in taut strings and longitudinal wave
propagation in rigid bars over the one-dimensional infinite interval I ={x |−∞<x<∞} or
semi-infinite interval I ={x |0 <x<∞}. We allow for an external force to act on the system,
and there is no damping. The nonhomogeneous partial differential equation in rectangular
coordinates is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
+h(x, t)
with the two initial conditions
u(x, 0) = f(x) and u
t
(x, 0) = g(x)
In Exercises 9.24 through 9.42, we seek solutions to the preceding equation in the form of a
Fourier integral with respect to x for various initial and boundary conditions. For the following
exercises, whenever possible, generate the animated solution for u(x, t) and plot the animated
sequence for 0 <t<5.

Infinite and Semi-infinite Spatial Domains 629
9.24. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier integral. Evaluate the integral either by
the inverse command or by direct integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = e
−
|x|
2
and g(x) = 0
9.25. Consider longitudinal motion in a rigid bar over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier integral. Evaluate the integral either by
the inverse command or by direct integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) = x e
−
|x|
2
9.26. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier integral. Evaluate the integral either by
the inverse command or by direct integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) =
1
1 +x
2
and g(x) = 0

630 Chapter 9
9.27. Consider longitudinal motion in a rigid bar over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier integral. Evaluate the integral either by
the inverse command or by direct integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) = e
−
x
2
4
9.28. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier integral. Evaluate the integral either by
the inverse command or by direct integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = x e
−
x
2
4
and g(x) = 0
9.29. Consider longitudinal motion in a rigid bar over the semi-infinite interval I ={x |0 <
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier sine integral. Evaluate the integral
either by the inverse command or by direct integration.
Boundary condition:
u(0,t)= 0 and
∞
0
|u(x, t)|dx<∞
Initial conditions:
f(x) = x e
−
x
2
and g(x) = 0

Infinite and Semi-infinite Spatial Domains 631
9.30. Consider Exercise 9.29. Develop the odd extension of f(x) and solve the problem by
the method of images.
9.31. Consider transverse motion in a taut string over the semi-infinite interval I ={x |0 <
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier sine integral. Evaluate the integral
either by the inverse command or by direct integration.
Boundary conditions:
u(0,t)= 0 and
∞
0
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) =
x
1 +x
2
9.32. Consider Exercise 9.31. Develop the odd extension of g(x) and solve the problem by
the method of images.
9.33. Consider longitudinal motion in a rigid bar over the semi-infinite interval I ={x |0 <
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier sine integral. Evaluate the integral
either by the inverse command or by direct integration.
Boundary conditions:
u(0,t)= 0 and
∞
0
|u(x, t)|dx<∞
Initial conditions:
f(x) = x e
−
x
2
4
and g(x) = 0
9.34. Consider Exercise 9.33. Develop the odd extension of f(x) and solve the problem by
the method of images.
9.35. Consider transverse motion in a taut string over the semi-infinite interval I ={x |0 <
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force acting and c = 1/2. Evaluate the wave
distribution u(x, t) in the form of a Fourier cosine integral. Evaluate the integral either
by the inverse command or by direct integration.

632 Chapter 9
Boundary conditions:
u
x
(0,t)= 0 and
∞
0
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) =
x
1 +x
2
9.36. Consider Exercise 9.35. Develop the even extension of g(x) and solve the problem by
the method of images.
9.37. Consider longitudinal motion in a rigid bar over the semi-infinite interval I ={x |0 <
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is no external force in the system and c = 1/2. Evaluate the
wave distribution u(x, t) in the form of a Fourier cosine integral. Evaluate the integral
either by the inverse command or by direct integration.
Boundary conditions:
u
x
(0,t)= 0 and
∞
0
|u(x, t)|dx<∞
Initial conditions:
f(x) = e
−
x
2
4
and g(x) = 0
9.38. Consider Exercise 9.37. Develop the even extension of f(x) and solve the problem by
the method of images.
9.39. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is an external force term h(x, t) (dimension of force per unit
mass) acting and c = 1/2. Evaluate the wave distribution u(x, t) in the form of a Fourier
integral. If possible, evaluate the integral either by the inverse command or by direct
integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) = 0

Infinite and Semi-infinite Spatial Domains 633
External driving force:
h(x, t) = e
−|x|
sin(t)
9.40. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is an external force term h(x, t) (dimension of force per unit
mass) acting and c = 1/2. Evaluate the wave distribution u(x, t) in the form of a Fourier
integral. If possible, evaluate the integral either by the inverse command or by direct
integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) = 0
External driving force:
h(x, t) =
x cos(t)
1 +x
2
9.41. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is an external force term h(x, t) (dimension of force per unit
mass) acting and c = 1/2. Evaluate the wave distribution u(x, t) in the form of a Fourier
integral. If possible, evaluate the integral either by the inverse command or by direct
integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) = 0
External driving force:
h(x, t) = e
−
x
2
4
sin(t)

634 Chapter 9
9.42. Consider transverse motion in a taut string over the infinite interval I ={x |−∞<
x<∞}. The initial displacement distribution f(x) and initial speed distribution g(x)
are given following. There is an external force term h(x, t) (dimension of force per unit
mass) acting and c = 1/2. Evaluate the wave distribution u(x, t) in the form of a Fourier
integral. If possible, evaluate the integral either by the inverse command or by direct
integration.
Boundary condition:
∞
−∞
|u(x, t)|dx<∞
Initial conditions:
f(x) = 0 and g(x) = 0
External driving force:
h(x, t) = x e
−
x
2
4
cos(t)
Fourier Integral Solutions of the Laplace Equation
We now consider problems involving the Laplace equation over infinite and semi-infinite
intervals. Recall that the Laplace equation was the time-invariant or steady-state solution to
either the wave or the diffusion equation. The Laplace equation reads
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
We now consider the solution of this equation, over intervals that may be infinite or
semi-infinite, using the method of Fourier transforms. The choice as to which of the two
variables we apply to the Fourier transform, with respect to either x or y, depends on the
boundary conditions impossed on the problem. Note that the temperature isotherms or
the electrostatic equipotential lines can be obtained by clicking on the graph and choosing the
“Render the plot using the polygon patch and contour style” option and then clicking the
“redraw” button in the graphics bar.
9.43. Consider the steady-state temperature distribution in a thin plate whose lateral surfaces
are insulated over the domain D ={(x, y) |−∞<x<∞, 0 <y<1}. The boundary
conditions are
u(x, 0) =
1
1 +x
2
and u(x, 1) = 0 and
∞
−∞
1
0
|u(x, y)|dy dx<∞
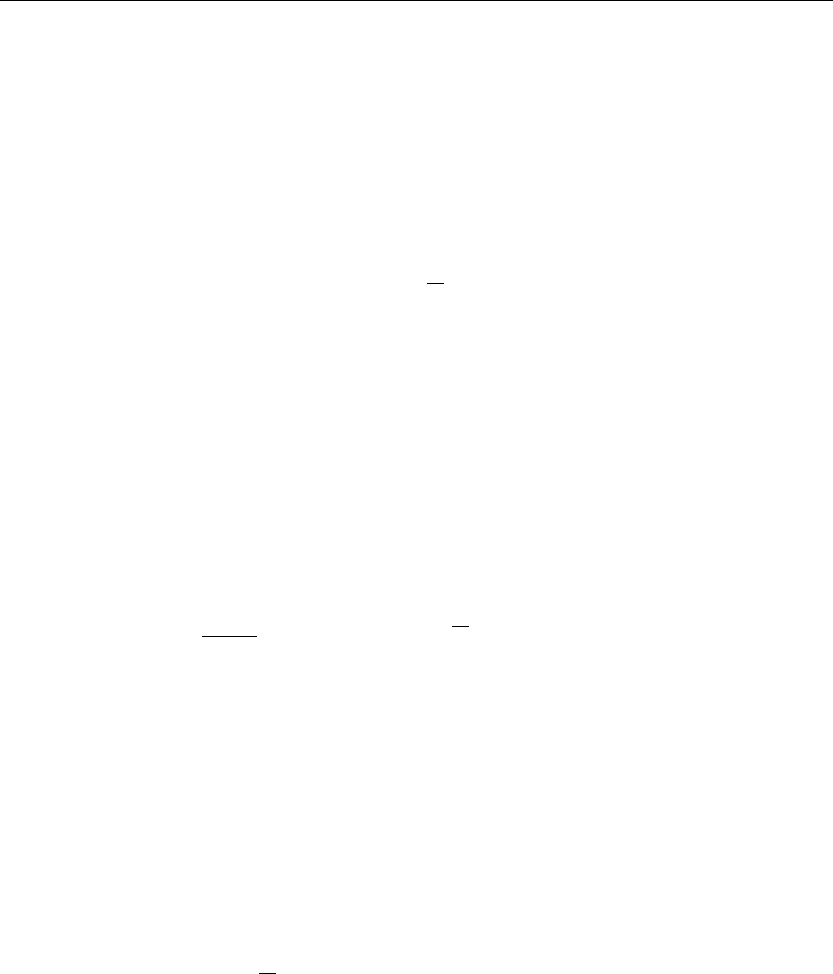
Infinite and Semi-infinite Spatial Domains 635
Obtain the solution as a Fourier integral with respect to x. If possible, evaluate the
Fourier integral (by the inverse or convolution method) and generate the
three-dimensional surface showing the isotherms over a portion of the problem
domain.
9.44. Consider the steady-state temperature distribution in a thin plate whose lateral surfaces
are insulated over the domain D ={(x, y) |−∞<x<∞, 0 <y<1}. The boundary
conditions are
u(x, 0) = 0 and u(x, 1) = e
−
x
2
4
and
∞
−∞
1
0
|u(x, y)|dy dx<∞
Obtain the solution as a Fourier integral with respect to x. If possible, evaluate
the Fourier integral (by the inverse or convolution method) and generate the
three-dimensional surface showing the isotherms over a portion of the problem
domain.
9.45. Consider the steady-state temperature distribution in a thin plate whose lateral surfaces
are insulated over the domain D ={(x, y) |−∞<x<∞, 0 <y<1}. The boundary
conditions are
u(x, 0) =
1
1 +x
2
and u(x, 1) = e
−
x
2
4
and
∞
−∞
1
0
|u(x, y)|dy dx<∞
Obtain the solution as a Fourier integral with respect to x. Show that the solution is a
superposition of the two solutions obtained in the two previous problems. If possible,
evaluate the Fourier integral (by the inverse or convolution method) and generate
the three-dimensional surface showing the isotherms over a portion of the problem
domain.
9.46. Consider the electrostatic potential distribution in a charge-free region over the domain
D ={(x, y) |−∞<x<∞, 0 <y<1}. The boundary conditions are
u(x, 0) = x e
−
x
2
4
and u(x, 1) = 0 and
∞
−∞
1
∞
|u(x, y)|dy dx<∞
Obtain the solution as a Fourier integral with respect to x. If possible, evaluate
the Fourier integral (by the inverse or convolution method) and generate the
three-dimensional surface showing the equipotential lines over a portion of the problem
domain.

636 Chapter 9
9.47. Consider the steady-state temperature distribution in a thin plate whose lateral surfaces
are insulated over the domain D ={(x, y) |0 <x<∞, −∞ <y<∞}. The boundary
conditions are
u(0,y)= e
−
y
2
4
and
∞
−∞
∞
0
|u(x, y)|dx dy<∞
Obtain the solution as a Fourier integral with respect to y. If possible, evaluate the
Fourier integral (by the inverse command or convolution method), and generate the
three-dimensional surface showing the isotherms over a portion of the problem domain.
9.48. Consider the electrostatic potential distribution in a charge-free region over the domain
D ={(x, y) |0 <x<1, −∞ <y<∞}. The boundary conditions are
u(0,y)= 0 and u(1,y)=
1
1 +y
2
and
∞
−∞
1
0
|u(x, y)|dx dy<∞
Obtain the solution as a Fourier integral with respect to y. If possible, evaluate
the Fourier integral (by the inverse or convolution method), and generate the
three-dimensional surface showing the equipotential lines over a portion of the problem
domain.
9.49. Consider the steady-state temperature distribution in a thin plate whose lateral surfaces
are insulated over the domain D ={(x, y) |0 <x<∞, 0 <y<∞}. The boundary
conditions are
u(0,y)= 0 and u(x, 0) = x e
−x
2
and
∞
0
∞
0
|u(x, y)|dx dy<∞
Obtain the solution as a Fourier sine integral with respect to x. If possible, evaluate the
Fourier integral (by the inverse command or convolution method), and generate the
three-dimensional surface showing the isotherms over a portion of the problem domain.
9.50. Consider Exercise 9.49. Generate the odd extension of u(x, 0) about the y-axis, and
solve by the method of images to obtain the solution as a Fourier integral with respect
to x. If possible, evaluate the Fourier integral (by the inverse command or convolution
method), and generate the three-dimensional surface showing the isotherms over a
portion of the problem domain.

Infinite and Semi-infinite Spatial Domains 637
9.51. Consider the electrostatic potential distribution in a charge-free region over the domain
D ={(x, y) |0 <x<∞, 0 <y<∞}. The boundary conditions are
u(0,y)=
y
1 +y
2
and u(x, 0) = 0 and
∞
0
∞
0
|u(x, y)|dx dy<∞
Obtain the solution as a Fourier sine integral with respect to y. If possible, evaluate
the Fourier integral (by the inverse or convolution method), and generate the
three-dimensional surface showing the equipotential lines over a portion of the problem
domain.
9.52. Consider Exercise 9.51. Generate the odd extension of u(0,y) about the x-axis, and
solve by the method of images to obtain the solution as a Fourier integral with respect
to y. If possible, evaluate the Fourier integral (by the inverse command or convolution
method) and generate the three-dimensional surface showing the equipotential lines
over a portion of the problem domain.
9.53. Consider the electrostatic potential distribution in a charge-free region over the domain
D ={(x, y) |0 <x<∞, 0 <y<∞}. The boundary conditions are
u(0,y)=
y
1 +y
2
and u(x, 0) = x e
−x
2
and
∞
0
∞
0
|u(x, y)|dx dy<∞
Note that we have nonhomogeneous boundary conditions with respect to both spatial
variables. Use the superposition method as outlined in the exercises of Chapter 5, and
show the solution to be a superposition of the two solutions obtained in Exercises 9.49
and 9.51. If possible, evaluate the Fourier integral (by the inverse or convolution
method), and generate the three-dimensional surface showing the equipotential lines
over a portion of the problem domain.
