Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


598 Chapter 9
Fourier transform of solution
> U(omega,t):=U(omega,0)*cos(omega*c*t)+V(omega,0)*sin(omega*c*t)/(omega*c);
U(ω, t) := −
1
2
Iω e
−
1
4
ω
2
√
π cos
1
2
ωt
(9.47)
Fourier integral solution
> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−infinity..infinity);
u(x, t) :=
∞
−∞
⎛
⎜
⎝
−
1
4
Iω e
−
1
4
ω
2
cos
1
2
ωt
e
Iωx
√
π
⎞
⎟
⎠
dω (9.48)
> u(x,t):=Heaviside(x)*simplify(invfourier(U(omega,t),omega,x));
u(x, t) := −
1
2
Heaviside(x)(t sinh(tx) −2x cosh(tx)) e
−x
2
−
1
4
t
2
(9.49)
ANIMATION
> animate(u(x,t),x=0..5,t=0..10,thickness=3);
The preceding animation command shows the spatial-time-dependent solution of the wave
amplitude u(x, t). The animation sequence here and in Figure 9.6 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..5,thickness=10);
1
0
0.1
20.1
20.2
0.2
0.3
0.4
23
x
45
Figure 9.6

Infinite and Semi-infinite Spatial Domains 599
EXAMPLE 9.10.3: (Solution by method of images) We seek the wave amplitude u(x, t) for
transverse waves on a long string over the semi-infinite interval I ={x |0 <x<∞}. The end
x = 0 is unsecured. The initial displacement distribution u(x, 0) = f(x) is given as follows, and
the initial speed distibution u
t
(x, 0) = 0. There are no external forces acting on the system, and
the wave speed is c = 1/2. We solve this problem using the method of images by forming the
even extension of f(x) and using the regular Fourier integral.
SOLUTION: The wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
The boundary conditions are that the solution be absolutely integrable over the interval and we
have a type 2 condition at x = 0:
∞
0
|u(x, t)|dx<∞ and u
x
(0,t)= 0
The initial conditions are
u(x, 0) = e
−x
2
and u
t
(x, 0) = 0
By the method of images, we use the Heaviside function H(x) to form the even extension
fe(x) of f(x) with the operation
fe(x) = f(x)H(x) +f(−x)H(−x)
The Fourier integral form of the solution is
u(x, t) =
∞
−∞
U(ω, t) e
iωx
2π
dω
Here, U(ω, t) satisfies the differential equation
∂
2
∂t
2
U(ω, t) +c
2
ω
2
U(ω, t) = 0
Assignment of system parameters
>restart:with(inttrans):with(plots):c:=1/2:f(x):=exp(−xˆ2):f(−x):=subs(x=−x,f(x)):g(x):=0:
g(−x):=subs(x=−x,g(x)):

600 Chapter 9
Formation of the even extension of f(x) and g(x)
> fe(x):=f(x)*Heaviside(x)+f(−x)*Heaviside(−x);
fe(x) := e
−x
2
Heaviside(x) + e
−x
2
Heaviside(−x) (9.50)
> ge(x):=g(x)*Heaviside(x)+g(−x)*Heaviside(−x);
ge(x) := 0 (9.51)
Fourier transform of initial conditions
> U(omega,0):=Int(fe(x)*exp(−I*omega*x),x=−infinity..infinity);U(omega,0):=value(%):
U(ω, 0) :=
∞
−∞
e
−x
2
Heaviside(x) + e
−x
2
Heaviside(−x)
e
−Iωx
dx (9.52)
> U(omega,0):=simplify(fourier(f(x),x,omega));
U(ω, 0) :=
√
π e
−
1
4
ω
2
(9.53)
> V(omega,0):=Int(ge(x)*exp(−I*omega*x),x=−infinity..infinity);V(omega,0):=value(%):
V(ω, 0) :=
∞
−∞
0dx (9.54)
> V(omega,0):=simplify(value(%));
V(ω, 0) := 0 (9.55)
Fourier transform of solution
> U(omega,t):=U(omega,0)*cos(omega*c*t)+V(omega,0)*sin(omega*c*t)/(omega*c);
U(ω, t) :=
√
π e
−
1
4
ω
2
cos
1
2
ωt
(9.56)
Fourier integral solution
> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−infinity..infinity);
u(x, t) :=
∞
−∞
1
2
e
−
1
4
ω
2
cos
1
2
ωt
e
Iωx
√
π
dω (9.57)
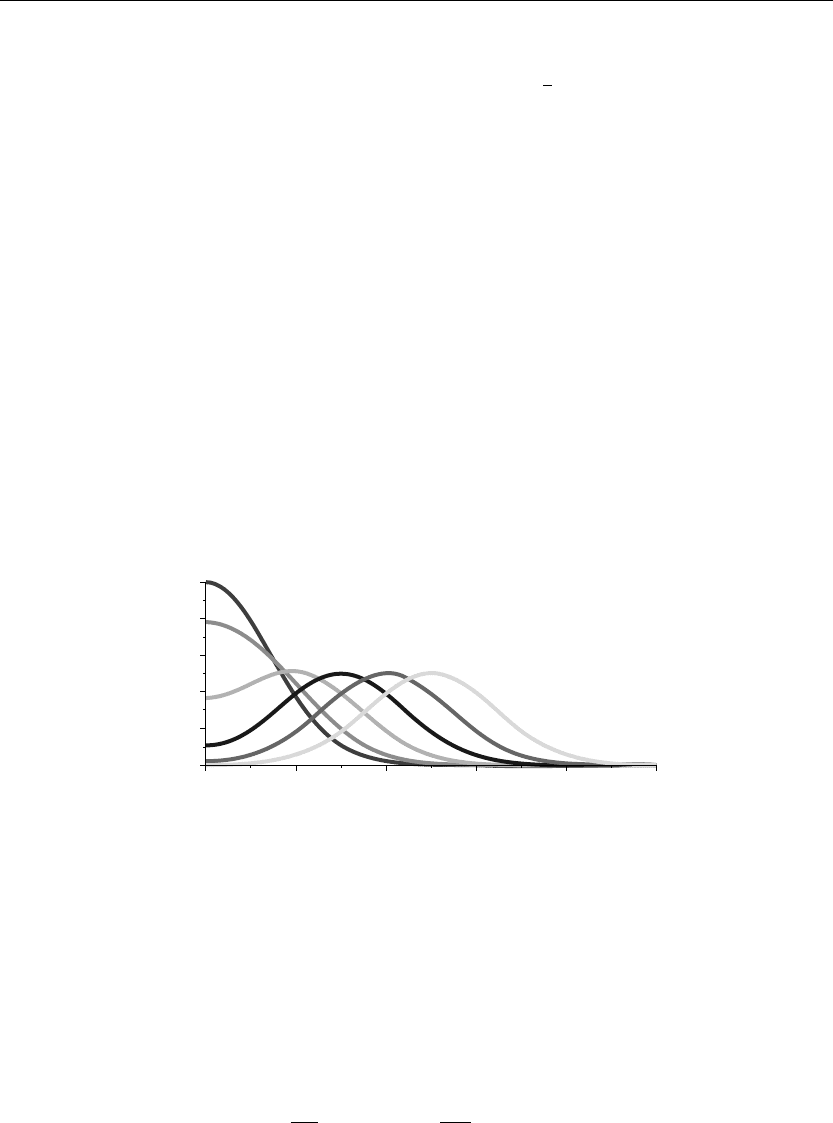
Infinite and Semi-infinite Spatial Domains 601
> u(x,t):=Heaviside(x)*(invfourier(U(omega,t),omega,x));
u(x, t) := Heaviside(x) cosh(tx) e
−
1
4
t
2
−x
2
(9.58)
ANIMATION
> animate(u(x,t),x=0..10,t=0..10,thickness=3);
The preceding animation command shows the spatial-time-dependent solution of the wave
amplitude u(x, t). The animation sequence here and in Figure 9.7 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..5,thickness=10);
x
0
0
0.2
0.4
0.6
0.8
1
12345
Figure 9.7
EXAMPLE 9.10.4: (Waves on an infinite string with initial speed) We seek the wave
amplitude u(x, t) for transverse wave motion on a long string over the infinite interval
I ={x |−∞<x<∞}. The string has an initial displacement u(x, 0) = 0 and an initial speed
distribution u
t
(x, 0) = g(x) given as follows. There are no external forces acting on the system,
and the wave speed is c = 1/2.
SOLUTION: The wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)

602 Chapter 9
The boundary conditions are that the solution be absolutely integrable over the interval; that is,
∞
−∞
|u(x, t)|dx<∞
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = e
−x
2
The Fourier integral form of the solution is
u(x, t) =
∞
−∞
U(ω, t) e
iωx
2π
dω
Here, U(ω, t) satisfies the differential equation
∂
2
∂t
2
U(ω, t) +c
2
ω
2
U(ω, t) = 0
Assignment of system parameters
> restart:with(inttrans):with(plots):c:=1/2:f(x):=0:g(x):=exp(−xˆ2):
Fourier transform of initial conditions
> U(omega,0):=Int(f(x)*exp(−I*omega*x),x=−infinity..infinity);U(omega,0):=value(%):
U(ω, 0) :=
∞
−∞
0dx (9.59)
> U(omega,0):=simplify(value(%));
U(ω, 0) := 0 (9.60)
> V(omega,0):=Int(g(x)*exp(−I*omega*x),x=−infinity..infinity);V(omega,0):=value(%):
V(ω, 0) :=
∞
−∞
e
−x
2
e
−Iωx
dx (9.61)

Infinite and Semi-infinite Spatial Domains 603
> V(omega,0):=simplify(fourier(g(x),x,omega));
V(ω, 0) := e
−
1
4
ω
2
√
π (9.62)
Fourier transform of solution
> U(omega,t):=U(omega,0)*cos(omega*c*t)+V(omega,0)*sin(omega*c*t)/(omega*c);
U(ω, t) :=
2e
−
1
4
ω
2
√
π sin
1
2
ωt
ω
(9.63)
Fourier integral solution
> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−infinity..infinity);
u(x, t) :=
∞
−∞
e
−
1
4
ω
2
sin
1
2
ωt
e
Iωx
√
πω
dω (9.64)
> u(x,t):=invfourier(U(omega,t),omega,x);
u(x, t) :=
1
2
√
π
−erf
x −
1
2
t
+erf
x +
1
2
t
(9.65)
ANIMATION
> animate(u(x,t),x=−5..5,t=0..5,thickness=3);
The preceding animation command shows the spatial-time-dependent solution of the wave
amplitude u(x, t). The animation sequence here and in Figure 9.8 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=-5..5,thickness=10);
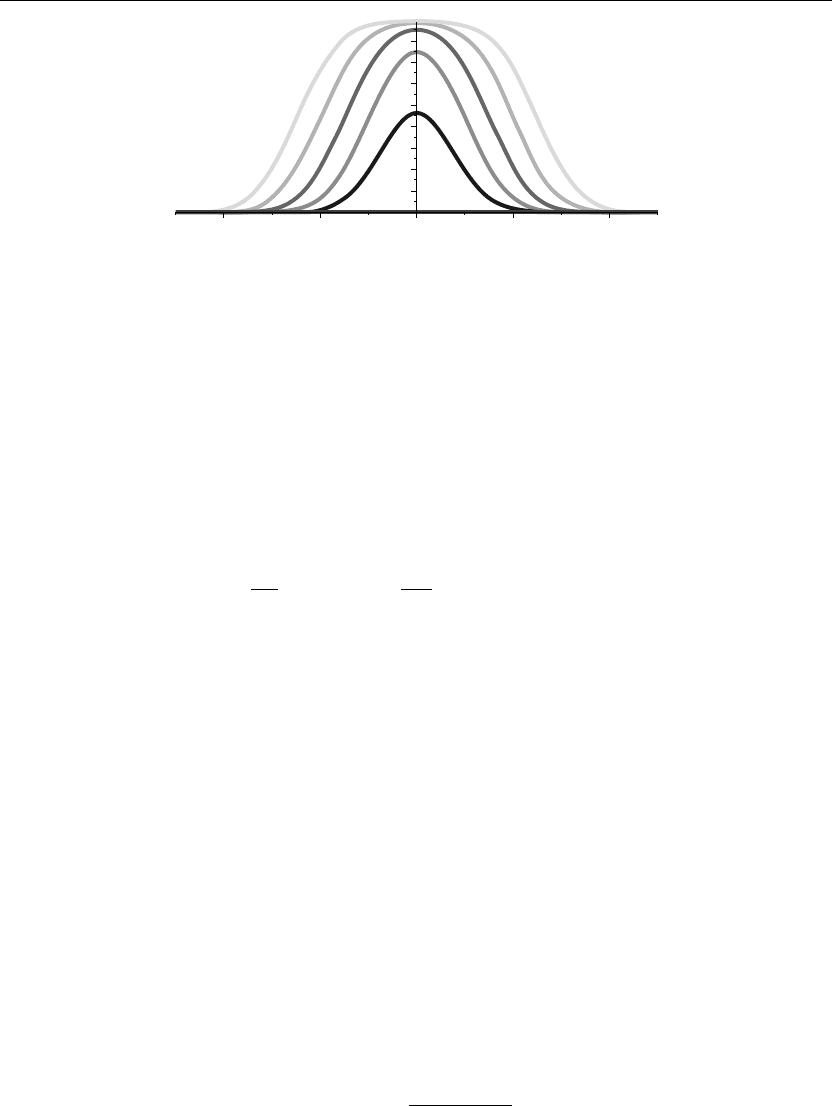
604 Chapter 9
0
0.2
24 22
0.4
0.6
1.2
1.4
1.6
1
0.8
2
x
4
Figure 9.8
EXAMPLE 9.10.5: (Waves on an infinite string with an external applied force) We seek the
wave amplitude u(x, t) for transverse wave motion on a long string over the infinite interval
I ={x |−∞<x<∞}. The string has an initial displacement u(x, 0) = 0 and an initial speed
distribution u
t
(x, 0) = 0. There is an external applied force h(x, t) acting on the system, and the
wave speed is c = 1/2.
SOLUTION: The nonhomogeneous wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
+h(x, t)
The boundary conditions are that the solution be absolutely integrable over the interval; that is,
∞
−∞
|u(x, t)|dx<∞
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = 0
The external applied force is
h(x, t) = e
−t
e
−x
2
The Fourier integral form of the solution is
u(x, t) =
∞
−∞
U(ω, t) e
iωx
2π
dω

Infinite and Semi-infinite Spatial Domains 605
Here, U(ω, t) satisfies the nonhomogeneous differential equation
∂
2
∂t
2
U(ω, t) +c
2
ω
2
U(ω, t) = H(ω, t)
Assignment of system parameters
> restart:with(inttrans):with(plots):c:=1/2:f(x):=0:g(x):=0:h(x,t):=exp(−t)*exp(−xˆ2):
Fourier transform of driving function
> H(omega,t):=Int(h(x,t)*exp(−I*omega*x),x=−infinity..infinity);H(omega,t):=
simplify(fourier(h(x,t),x,omega)):
H(ω, t) :=
∞
−∞
e
−t
e
−x
2
e
−Iωx
dx (9.66)
> H(omega,t):=simplify(value(%));H(omega,tau):=subs(t=tau,H(omega,t)):
H(ω, t) :=
√
π e
−t−
1
4
ω
2
(9.67)
Fourier transform of solution
> U(omega,t):=Int(H(omega,tau)*sin(omega*c*(t−tau))/(omega*c),tau=0..t);
U(ω, t) :=
t
0
2
√
π e
−τ−
1
4
ω
2
sin
1
2
ω(t −τ)
ω
dτ (9.68)
> U(omega,t):=simplify(value(%));
U(ω, t) := −
4
√
π e
−t−
1
4
ω
2
e
t
ω cos
1
2
ωt
−2e
t
sin
1
2
ωt
−ω
ω
4 +ω
2
(9.69)
Fourier integral solution
> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−infinity..infinity);
u(x, t) :=
∞
−∞
⎛
⎜
⎝
−
2e
−t−
1
4
ω
2
e
t
ω cos
1
2
ωt
−2e
t
sin
1
2
ωt
−ω
e
Iωx
√
πω
4 +ω
2
⎞
⎟
⎠
dω (9.70)
We leave this solution in integral form.

606 Chapter 9
9.11 Laplace Equation over Infinite and Semi-infinite
Domains
We now consider the Laplace equation, which is the steady-state version of both the diffusion
and the wave partial differential equations. Recall from Chapter 5 that these equations were a
result of considering all solutions to be time invariant, thus forcing all time derivative terms
equal to 0. We will use the Fourier integral method (singular eigenfunction expansion) to
formulate the solutions to these partial differential equations over infinite or semi-infinite
intervals.
We consider the homogeneous Laplace partial differential equation in two dimensions in the
rectangular coordinate system where one of the coordinates is of infinite or semi-infinite extent.
∂
2
∂x
2
u(x, y) +
∂
2
∂y
2
u(x, y) = 0
Using the method of separation of variables as in Chapter 5, we arrive at two ordinary
differential equations: one in x and one in y. To obtain solutions that are finite as the variable x
or y approaches infinity, we purposely select the format of the differential equations so as to
satisfy this condition. Thus, depending on which variable, x or y, is infinite or semi-infinite in
extent, we write the separated equations accordingly.
For example, if the domain is infinite or semi-infinite in extent with respect to the x variable,
then we write the two separated equations as
d
2
dx
2
X(x)+λX(x) = 0
and
d
2
dy
2
Y(y) −λY(y) = 0
A set of basis vectors for the x equation for λ>0 is, from Chapter 1,
x1(x) = e
i
√
λx
and
x2(x) = e
−i
√
λx
If we set λ = ω
2
, then we satisfy the condition that our x-dependent portion of the solution be
bounded as x goes to plus or minus infinity. Therefore, the x-dependent orthonormalized
singular eigenfunctions, as shown in Section 9.2, can be written as
√
2e
iωx
2
√
π
for −∞ <ω<∞.

Infinite and Semi-infinite Spatial Domains 607
From the Fourier integral theorem, the singular eigenfunctions are “complete” with respect to
piecewise smooth and absolutely integrable functions over the infinite domain. Thus, we can
write our solution as the superposition of the singular eigenfunctions just given, or,
equivalently, as the Fourier integral
u(x, y) =
∞
−∞
U(ω, y) e
iωx
2π
dω
From Section 9.2, U(ω, y) is the Fourier transform of u(x, y) with respect to the variable x.
If we substitute the assumed solution into the partial differential equation, and we assume the
validity of the formal interchange between the differentiation and the integration operators,
then we get the following differential equation in y:
∂
2
∂y
2
U(ω, y) −ω
2
U(ω, y) = 0
From Chapter 1, a set of basis vectors for the preceding corresponding homogeneous
differential equation is
y1(y) = e
ωy
and
y2(y) = e
−ωy
The solution to the preceding y-dependent differential equation is
U(ω, y) = A(ω) e
ωy
+B(ω) e
−ωy
Thus, from the given transform, the solution to our homogeneous partial differential equation
can be written as the Fourier integral
u(x, y) =
∞
−∞
A(ω) e
ωy
+B(ω) e
−ωy
e
iωx
2π
dω
The Fourier coefficients A(ω) and B(ω) are determined from the boundary conditions imposed
on the problem.
In a similar manner, if the domain is infinite or semi-infinite in extent with respect to the y
variable, then we write the two separated equations as
d
2
dy
2
Y(y) +λY(y) = 0
