Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

578 Chapter 9

0.2

0.4

0.6

0.8

222424

Figure 9.2

We note here that the initial condition function f(x) is not absolutely integrable over the inﬁnite

domain, and we would not have been able to solve the preceding by the transform method. The

convolution method is more forgiving on the conditions for f(x) in that it just requires that f(x)

be ﬁnite over the domain. For some problems, the convolution method is the preferred method.

EXAMPLE 9.7.4: (Fourier sine integral solution) We seek the temperature distribution u(x, t)

in a thin, long rod over the semi-inﬁnite interval I ={x |0 <x<∞} whose lateral surface is

insulated. The end x = 0 is held ﬁxed at temperature 0. The initial temperature distribution

u(x, 0) = f(x) is given as follows. There is no source term in the system, and the thermal

diffusivity is k = 1/4.

SOLUTION: The diffusion partial differential equation is

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



The boundary conditions are that the solution should be absolutely integrable over the interval

and we have a type 1 condition at x = 0:

∞



|u(x, t)|dx<∞ and u(0,t)= 0

The initial condition is

u(x, 0) = 10 x e

−x

Due to the type 1 condition at the origin, we choose the Fourier sine integral form of solution:

u(x, t) =

∞



2U(ω, t) sin(ωx)

dω

Inﬁnite and Semi-inﬁnite Spatial Domains 579

Here, U(ω, t) satisﬁes the differential equation

∂

∂t

U(ω, t) +kω

U(ω, t) = 0

Assignment of system parameters

> restart:with(plots):k:=1/4:f(x):=10*x*exp(−xˆ2):

Fourier sine transform of initial condition term

> U(omega,0):=Int(f(x)*sin(omega*x),x=0..inﬁnity);

U(ω, 0) :=

∞



10 x e

−x

sin(ωx) dx (9.13)

> U(omega,0):=simplify(value(%));

U(ω, 0) :=

√

πω e

−

(9.14)

Fourier sine transform of solution

> U(omega,t):=U(omega,0)*exp(−k*omegaˆ2*t);

U(ω, t) :=

√

πωe

−

(9.15)

Fourier sine integral solution

> u(x,t):=Int(U(omega,t)*(2/Pi)*sin(omega*x),omega=0..inﬁnity);assume(t>0):

u(x, t) :=

∞



5ω e

−

sin(ωx)

√

dω (9.16)

> u(x,t):=simplify(value(%));

u(x, t∼) :=

10 x e

−

1+t∼

(1 +t∼)

3/2

(9.17)

ANIMATION

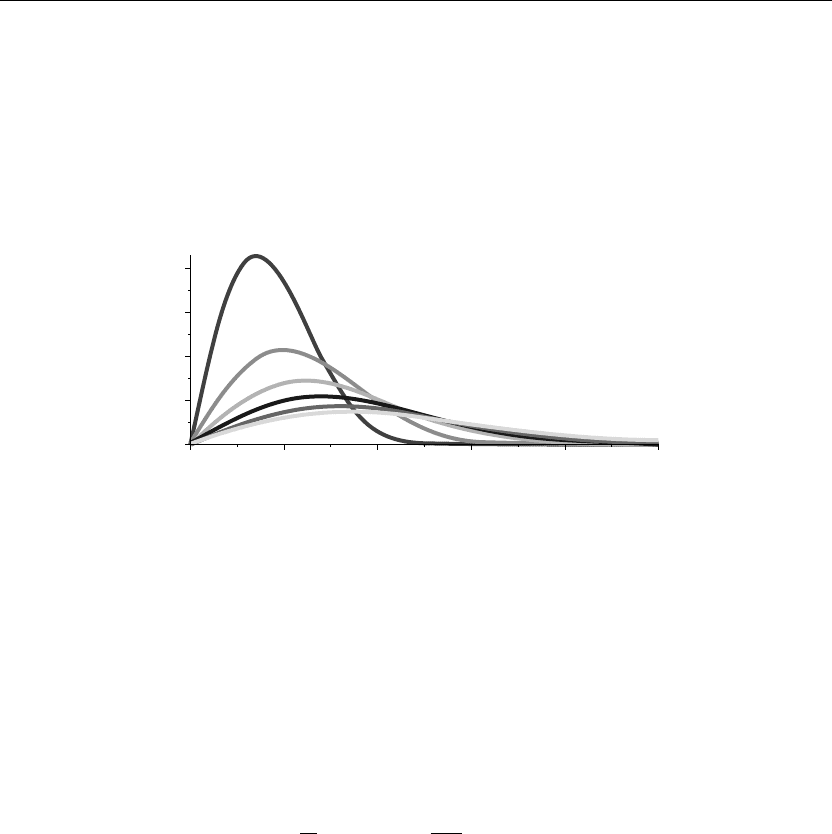
> animate(u(x,t),x=0..5,t=0..5,thickness=3);

The preceding animation command shows the spatial-time-dependent solution of the

temperature u(x, t) in the medium. The animation sequence here and in Figure 9.3 shows

snapshots of the animation at times t = 0, 1, 2, 3, 4, 5.

580 Chapter 9

ANIMATION SEQUENCE

> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):

> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):

> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):

> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)}x=0..5,thickness=10);

34510

Figure 9.3

EXAMPLE 9.7.5: (Solution by the method of images) Here we consider the same problem as

in Example 9.7.4, except now we use the method of images, which allows for use of the regular

Fourier integral. Because the boundary conditions are homogeneous and of type 1 at x = 0, we

reﬂect the initial condition function u(x, 0) = f(x) about the origin, thus forming its odd

extension onto the negative portion of the x-axis. Since we are only interested in the solution

for x>0, we will ignore that portion for x<0.

SOLUTION: The diffusion partial differential equation is

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



The boundary conditions are that the solution be absolutely integrable over the interval, and we

have a type 1 condition at x = 0:

∞



|u(x, t)|dx<∞ and u(0,t)= 0

The initial condition is

u(x, 0) = 10 x e

−x

Inﬁnite and Semi-inﬁnite Spatial Domains 581

By the method of images, we use the Heaviside function H(x) to form the odd extension fo(x)

of f(x) with the operation

fo(x) = f(x)H(x) −f(−x)H(−x)

The Fourier integral form of the solution is

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

Here, U(ω, t) satisﬁes the differential equation

∂

∂t

U(ω, t) +kω

U(ω, t) = 0

Assignment of system parameters

> restart:with(plots):k:=1/4:f(x):=10*x*exp(−xˆ2):f(−x):=subs(x=−x,f(x)):

Formation of the odd extension of f(x)

> fo(x):=f(x)*Heaviside(x)−f(−x)*Heaviside(−x);

fo(x) := 10x e

−x

Heaviside(x) +10x e

−x

Heaviside(−x) (9.18)

Fourier transform of odd extension of initial condition term

> U(omega,0):=Int(−f(−x)*exp(−I*omega*x),x=−inﬁnity..0)+Int(f(x)*exp(−I*omega*x),

x=0..inﬁnity);

U(ω, 0) :=



−∞

10x e

−x

−Iωx

dx +

∞



10x e

−x

−Iωx

dx (9.19)

> U(omega,0):=simplify(value(%));

U(ω, 0) := −5Iω

√

π e

−

(9.20)

Fourier transform of solution

> U(omega,t):=U(omega,0)*exp(−k*omegaˆ2*t);

U(ω, t) := −5Iω

√

π e

−

(9.21)

582 Chapter 9

Fourier integral solution

> u(x,t):=Int(U(omega,t)*(1/(2*Pi))*exp(I*omega*x),omega=−inﬁnity..inﬁnity);assume(t>0):

u(x, t) :=

∞



−∞

⎛

⎝

−

Iω e

−

Iωx

√

⎞

⎠

dω (9.22)

> u(x,t):=simplify(value(%));

u(x, t∼) :=

10 e

−

1+t∼

(1 +t∼)

3/2

(9.23)

Note that we arrive at the exact same solution as we did when using the Fourier sine transform

method.

EXAMPLE 9.7.6: (Fourier cosine integral solution) We seek the temperature distribution u(x, t)

in a long, thin rod over the semi-inﬁnite interval I ={x |0 <x<∞}whose lateral surface is

insulated and whose left end is insulated at x = 0. The initial temperature distribution in the rod

u(x, 0) = f(x) is given as follows. There is no source term in the system and the thermal

diffusivity is k = 1/4.

SOLUTION: The diffusion partial differential equation is

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



The boundary conditions are that the solution be absolutely integrable over the interval, and we

have a type 2 condition at x = 0:

∞



|u(x, t)|dx<∞ and u

(0,t)= 0

The initial condition is

u(x, 0) = 10 e

−x

Due to the type 2 condition at the origin, we choose the Fourier cosine integral form of solution:

u(x, t) =

∞



2U(ω, t) cos(ωx)

dω

Here, U(ω, t) satisﬁes the differential equation

∂

∂t

U(ω, t) +kω

U(ω, t) = 0

Inﬁnite and Semi-inﬁnite Spatial Domains 583

Assignment of system parameters

> restart:with(plots):k:=1/4:f(x):=10*exp(−xˆ2):

Fourier cosine transform of initial condition term

> U(omega,0):=Int(f(x)*cos(omega*x),x=0..inﬁnity);

U(ω, 0) :=

∞



10 e

−x

cos(ωx) dx (9.24)

> U(omega,0):=simplify(value%));

U(ω, 0) := 5

√

π e

−

(9.25)

Fourier cosine transform of solution

> U(omega,t):=U(omega,0)*exp(−k*omegaˆ2*t);

U(ω, t) := 5

√

π e

−

(9.26)

Fourier cosine integral solution

> u(x,t):=Int(U(omega,t)*(2/Pi)*cos(omega*x),omega=0..inﬁnity);assume(t>0):

u(x, t) :=

∞



10 e

−

cos(ωx)

√

dω (9.27)

> u(x,t):=simplify(value(%));

u(x, t∼) :=

10 e

−

1+t∼

√

1 +t∼

(9.28)

ANIMATION

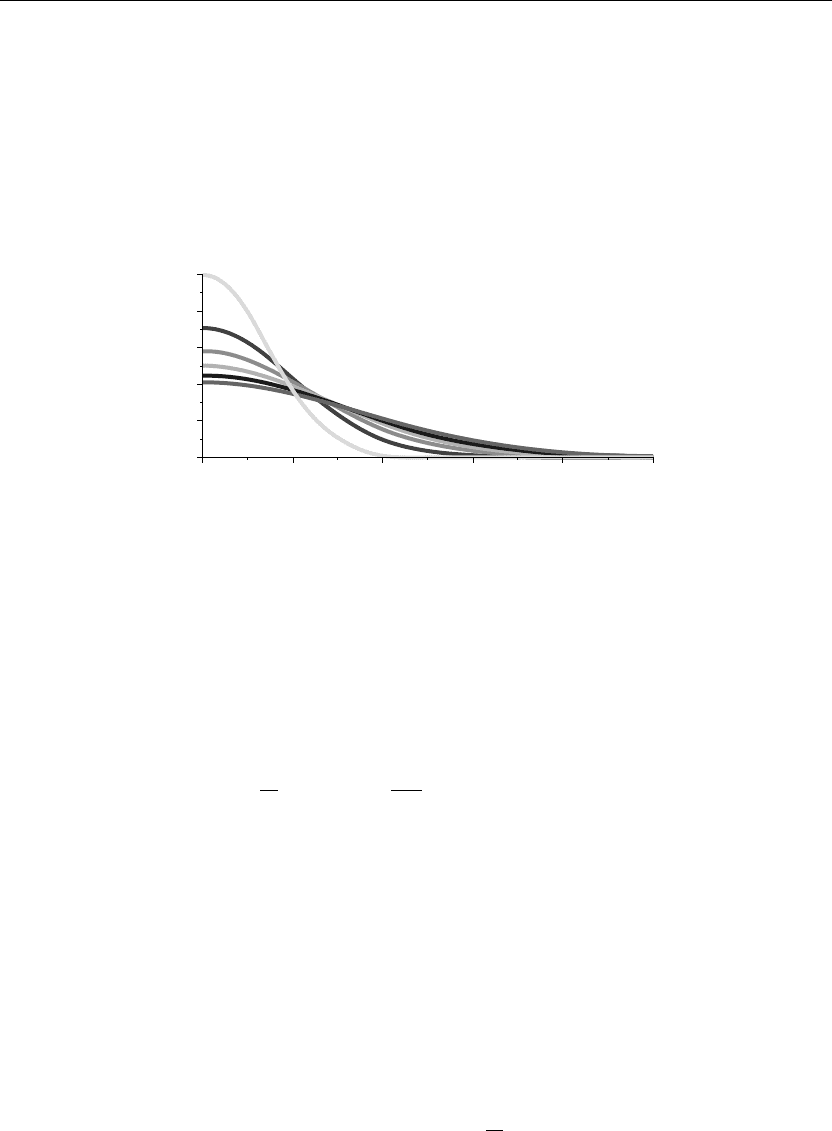
> animate(u(x,t),x=0..5,t=0..5,thickness=3);

The preceding animation command shows the spatial-time-dependent solution of the

temperature u(x, t) in the medium. The animation sequence here and in Figure 9.4 shows

snapshots of the animation at times t = 0, 1, 2, 3, 4, 5.

584 Chapter 9

ANIMATION SEQUENCE

> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):

> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):

> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):

> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)}x=0..5,thickness=10);

345

Figure 9.4

EXAMPLE 9.7.7: (Solution in integral form) We seek the temperature distribution u(x, t)

in a long, thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The rod has an internal heat source h(x, t) given as follows. The initial

temperature distribution along the rod is 0, and the thermal diffusivity of the rod is k = 1.

SOLUTION: The nonhomogeneous diffusion partial differential equation is

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



+h(x, t)

The boundary condition is that the solution be absolutely integrable over the interval; that is,

∞



−∞

|u(x, t)|dx<∞

The initial condition is

u(x, 0) = 0

The internal source term is

h(x, t) = sin(t) e

−

Inﬁnite and Semi-inﬁnite Spatial Domains 585

The Fourier integral form of the solution is

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

Here, U(ω, t) satisﬁes the nonhomogeneous differential equation

∂

∂t

U(ω, t) +kω

U(ω, t) = H(ω, t)

Assignment of system parameters

> restart:with(plots):k:=1:h(x,t):=sin(t)*exp(−xˆ2/4):

Fourier transform of source term

> H(omega,t):=Int(h(x,t)*exp(−I*omega*x),x=−inﬁnity..inﬁnity);U(omega,0):=value(%):

H(ω, t) :=

∞



−∞

sin(t) e

−

−Iωx

dx (9.29)

> H(omega,t):=simplify(value(%));H(omega,tau):=subs(t=tau,H(omega,t)):

H(ω, t) := 2e

−ω

sin(t)

√

π (9.30)

Fourier transform of solution

> U(omega,t):=Int(H(omega,tau)*exp(−k*omegaˆ2*(t−tau)),tau=0..t);

U(ω, t) :=



−ω

sin(τ)

√

π e

−ω

(t−τ)

dτ (9.31)

> U(omega,t):=simplify(factor(value(%)));

U(ω, t) :=

√



1 − e

cos(t) + e

sin(t)



−ω

(1+t)

(9.32)

Fourier integral solution

> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−inﬁnity..inﬁnity);

u(x, t) :=

∞



−∞



1 − e

cos(t) + e

sin(t)



−ω

(1+t)

Iωx

√





dω (9.33)

We leave this answer in integral form.

586 Chapter 9

9.8 Nonhomogeneous Wave Equation over Inﬁnite Domains

As we did earlier for the diffusion equation, here we use the Fourier integral method (singular

eigenfunction expansion) to formulate the solutions to the wave partial differential equations

over inﬁnite or semi-inﬁnite intervals.

We ﬁrst consider the nonhomogeneous wave partial differential equation over the inﬁnite

interval I ={x |−∞<x<∞} with no damping in the system

∂

∂t

u(x, t) = c



∂

∂x

u(x, t)



+h(x, t)

with the two initial conditions

u(x, 0) = f(x) and u

(x, 0) = g(x)

where f(x) denotes the initial displacement of the wave, g(x) denotes the initial speed of the

wave, and h(x, t) accounts for any external forces acting on the system. The boundary

conditions are such that we require u(x, t) to be piecewise smooth and absolutely integrable

over the interval I.

As we did in Chapter 8, we ﬁrst consider the homogeneous version of the preceding equation.

Using the method of separation of variables, as in Chapter 3, we arrive at two ordinary

differential equations: one in t and one in x. The x-dependent differential equation is, again,

of the Euler type and it reads

X(x)+λX(x) = 0

A set of basis vectors of the preceding differential equation, for λ>0, is, from Chapter 1,

x1(x) = e

√

λx

and

x2(x) = e

−i

√

λx

If we set λ = ω

and we require that our x-dependent portion of the solution be bounded as x

goes to plus or minus inﬁnity, then our x-dependent, orthonormalized singular eigenfunctions,

as shown in Section 9.2, can be written

√

iωx

√

for −∞ <ω<∞.

From the Fourier integral theorem, these singular eigenfunctions are “complete” with respect

to piecewise smooth and absolutely integrable functions over the inﬁnite domain. Thus, we can

Inﬁnite and Semi-inﬁnite Spatial Domains 587

write our solution as the superposition of the given singular eigenfunctions, or, equivalently, as

the Fourier integral

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

From Section 9.2, U(ω, t) is the time-dependent Fourier transform of u(x, t). If we substitute

the two initial conditions into this solution, we get

f(x) =

∞



−∞

U(ω, 0) e

iωx

2π

dω

and

g(x) =

∞



−∞

V(ω, 0) e

iωx

2π

dω

Here, U(ω, 0) is the Fourier transform of the initial displacement function f(x) and V(ω, 0) is

the Fourier transform of the initial speed function g(x). We must assume that f(x) and g(x) are

both piecewise smooth and absolutely integrable over the inﬁnite interval.

We now deal with the nonhomogeneous driving term in the same manner as we did in

Chapter 8. If the source term h(x, t) is piecewise smooth and absolutely integrable with respect

to x over the inﬁnite domain, then we can express its Fourier integral as

h(x, t) =

∞



−∞

H(ω, t) e

iωx

2π

dω

where H(ω, t) is the Fourier transform of h(x, t).

We now require that all of the preceding functions behave in the same manner as for the

diffusion equation in Section 9.4; that is, if we substitute the assumed solution into the given

partial differential equation, and we assume validity of the formal interchange between the

differentiation and the integration operators, then we get the following equation:

∞



−∞



∂

∂t

U(ω, t) +c

U(ω, t)



iωx

dω =

∞



−∞

H(ω, t) e

iωx

dω

In order for this equation to hold, due to the linear independence of the singular eigenfunctions,

we set the integrands equal to each other and arrive at the following second-order