Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

588 Chapter 9

nonhomogeneous differential equation in the time variable t:

∂

∂t

U(ω, t) +c

U(ω, t) = H(ω, t)

with the two initial conditions

U(ω, 0) =

∞



−∞

f(x) e

−iωx

and

V(ω, 0) =

∞



−∞

g(x) e

−iωx

This is a second-order initial value problem and, from Chapter 1, Section 1.8, the solution to

the preceding differential equation is

U(ω, t) = U(ω, 0) cos(ωct) +

V(ω, 0) sin(ωct)

ωc



H(ω, τ) sin(ωc(t −τ))

ωc

dτ

Thus, from the preceding transform, the solution to our nonhomogeneous partial differential

equation can be written as the Fourier integral

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

where U(ω, t) is the solution to the preceding time equation.

9.9 Wave Equation over Semi-inﬁnite Domains

We now consider the same problem as in the preceding section, but for a semi-inﬁnite interval

I ={x |0 <x<∞}. We continue to assume that all functions are piecewise smooth and

absolutely integrable with respect to x over the semi-inﬁnite interval. Depending on the

boundary condition at x = 0, we will utilize those singular eigenfunctions that are consistent

with the boundary condition.

If at x = 0 we have the type 1 condition

u(0,t)= 0

Inﬁnite and Semi-inﬁnite Spatial Domains 589

then the appropriate singular orthonormalized eigenfunctions, from Section 9.3, are given as

√

2 sin(ωx)

√

for 0 <ω<∞. Thus, we can write our solution in terms of the singular eigenfunctions as

u(x, t) =

∞



2U(ω, t) sin(ωx)

dω

From Section 9.3, U(ω, t) is the time-dependent Fourier sine transform of u(x, t).Ifwe

substitute the initial conditions into this solution, we get

f(x) =

∞



2U(ω, 0) sin(ωx)

dω

and

g(x) =

∞



2V(ω, 0) sin(ωx)

dω

Here, U(ω, 0) is the Fourier sine transform of the initial condition function f(x), and V(ω, 0) is

the Fourier sine transform of the initial speed function g(x); that is,

U(ω, 0) =

∞



f(x) sin(ωx) dx

and

V(ω, 0) =

∞



g(x) sin(ωx) dx

In a similar manner, the source term h(x, t) can be expressed as the Fourier sine integral

h(x, t) =

∞



2H(ω, t) sin(ωx)

dω

where H(ω, t) is now the Fourier sine transform of h(x, t); that is,

H(ω, t) =

∞



h(x, t) sin(ωx) dx

590 Chapter 9

Proceeding formally as we did earlier, the solution for U(ω, t) is

U(ω, t) = U(ω, 0) cos(ωct) +

V(ω, 0) sin(ωct)

ωc



H(ω, τ) sin(ωc(t −τ))

ωc

dτ

Thus, the ﬁnal solution to our nonhomogeneous wave partial differential equation over the

semi-inﬁnite interval, with type 1 conditions at the origin, can be written as the Fourier sine

integral

u(x, t) =



∞

2U(ω, t) sin(ωx) dω

where U(ω, t) was given above.

On the other hand, if, at x = 0, we have the type 2 condition

(0,t)= 0

then the appropriate singular orthonormalized eigenfunctions, from Section 9.3, are given as

√

2 cos(ωx)

√

for 0 <ω<∞.

Thus, we can write our solution in terms of the singular eigenfunctions as

u(x, t) =

∞



2U(ω, t) cos(ωx)

dω

From Section 9.3, U(ω, t) is the time-dependent Fourier cosine transform of u(x, t).Ifwe

substitute the two initial conditions on this solution, we get

f(x) =

∞



2U(ω, 0) cos(ωx)

dω

and

g(x) =

∞



2V(ω, 0) cos(ωx)

dω

Inﬁnite and Semi-inﬁnite Spatial Domains 591

Here, U(ω, 0) is the Fourier cosine transform of the initial condition function f(x), and V(ω, 0)

is the Fourier cosine transform of the initial speed function g(x); that is,

U(ω, 0) =

∞



f(x) cos(ωx) dx

and

V(ω, 0) =

∞



g(x) cos(ωx) dx

In a similar manner, the source term h(x, t) can be expressed as the Fourier cosine integral

h(x, t) =

∞



2H(ω, t) cos(ωx)

dω

where H(ω, t) is now the Fourier cosine transform of h(x, t); that is,

H(ω, t) =

∞



h(x, t) cos(ωx) dx

Proceeding formally as we did earlier, the solution for U(ω, t) is again

U(ω, t) = U(ω, 0) cos(ωct) +

V(ω, 0) sin(ωct)

ωc



H(ω, τ) sin(ωc(t −τ))

ωc

dτ

Thus, the ﬁnal solution to our nonhomogeneous wave partial differential equation over the

semi-inﬁnite interval, with type 2 boundary conditions at the origin, can be written as the

Fourier cosine integral

u(x, t) =

∞



2U(ω, t) cos(ωx)

dω

where U(ω, t) was given above.

Similar to the case for diffusion problems, the method of images can also be used for the wave

equation problems over semi-inﬁnite domains. We now demonstrate this concept by solving an

illustrative problem.

DEMONSTRATION: We seek the wave amplitude u(x, t) for transverse waves on a long

string over the semi-inﬁnite interval I ={x |0 <x<∞}, which is unsecured at x = 0.

592 Chapter 9

The initial displacement of the string u(x, 0) = f(x) is given as follows, and the initial speed

distribution u

(x, 0) = g(x) has the value 0. There are no external forces acting on the string,

and the wave speed is c = 1/2.

SOLUTION: For transverse waves on a string, the homogeneous wave partial differential

equation is

∂

∂t

u(x, t) =

∂

∂x

u(x, t)

Because the string is unsecured at the end point x = 0 and we require the solution to be

absolutely integrable over the semi-inﬁnite inteval I, the system boundary conditions are

(0,t)= 0 and

∞



|u(x, t)|dx<∞

The initial displacement function of the string is given as u(x, 0) = f(x) where

f(x) = e

−x

and the initial speed distribution is given as u

(x, 0) = g(x) where

g(x) = 0

We can solve this problem by using either the method of the Fourier cosine transform, as

discussed earlier, or we can use the equivalent method of images. We choose the method of

images here.

Using the Heaviside function, we establish the even extension fe(x) of the initial displacement

distribution f(x) by reﬂecting it about the y-axis as follows:

fe(x) = e

−x

H(x) +e

−x

H(−x)

and the even extension of the initial speed distribution is

ge(x) = 0

With the even extensions of the initial displacement and speed distributions deﬁned over the

inﬁnite interval I ={x |−∞<x<∞}, we can now use the method of the Fourier integral and

write the solution as

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

Inﬁnite and Semi-inﬁnite Spatial Domains 593

Substitution of this solution into the partial differential equation, as we did in Section 9.8,

yields the time-dependent ordinary differential equation

∂

∂t

U(ω, t) +

U(ω, t)

= 0

We must now solve this differential equation subject to the given initial conditions. Evaluation

of the transform of the initial displacement function fe(x) (note the function in this case is

already even) yields

U(ω, 0) =

∞



−∞

−x

−iωx

which is evaluated to be

U(ω, 0) =

√

πe

−

Similarly, evaluation of the transform of the initial speed distribution ge(x) yields

V(ω, 0) = 0

Thus, from Section 9.8, the solution to the time-dependent differential equation for the Fourier

transform U(ω, t), subject to the two initial conditions, is

U(ω, t) =

√

πe

−

cos



ωt



Finally, from this known transform, the Fourier integral form of the solution is given as

u(x, t) =

∞



−∞

−

cos



ωt



√

dω

Evaluation of this integral yields the solution for the string displacement

u(x, t) =



−2xt



−

(2x−t)

for x>0.

The details for the solution of this problem along with the graphics are given later in one of the

Maple worksheet examples.

594 Chapter 9

9.10 Example Wave Equation Problems over Inﬁnite and

Semi-inﬁnite Domains

We now consider solutions to some wave equation problems over inﬁnite and semi-inﬁnite

domains. We use the procedures from the preceding section to develop our solutions.

EXAMPLE 9.10.1: (Waves on an inﬁnite string) We seek the wave amplitude u(x, t) for

transverse wave motion on a long string over the inﬁnite interval I ={x |−∞<x<∞},

which has an initial displacement u(x, 0) = f(x) given as follows. The initial speed distribution

(x, 0) = g(x) is 0, there are no external forces acting on the system, and the wave speed is

c = 1/2.

SOLUTION: The wave partial differential equation is

∂

∂t

u(x, t) = c



∂

∂x

u(x, t)



The boundary condition is that the solution be absolutely integrable over the interval; that is,

∞



−∞

|u(x, t)|dx<∞

The initial conditions are

u(x, 0) = e

−x

and u

(x, 0) = 0

The Fourier integral form of the solution is

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

Here, U(ω, t) satisﬁes the differential equation

∂

∂t

U(ω, t) +c

U(ω, t) = 0

Assignment of system parameters

> restart:with(inttrans):with(plots):c:=1/2:f(x):=exp(−xˆ2):g(x):=0:

Fourier transform of initial conditions

> U(omega,0):=Int(f(x)*exp(−I*omega*x),x=−inﬁnity..inﬁnity);U(omega,0):=value(%):

U(ω, 0) :=

∞



−∞

−x

−Iωx

dx (9.34)

Inﬁnite and Semi-inﬁnite Spatial Domains 595

> U(omega,0):=simplify(value(%));

U(ω, 0) := e

−

√

π (9.35)

> V(omega,0):=Int(g(x)*exp(−I*omega*x),x=−inﬁnity..inﬁnity);V(omega,0):=value(%):

V(ω, 0) :=

∞



−∞

0dx (9.36)

> V(omega,0):=simplify(value(%));

V(ω, 0) := 0 (9.37)

Fourier transform of solution

> U(omega,t):=U(omega,0)*cos(omega*c*t)+V(omega,0)*sin(omega*c*t)/(omega*c);

U(ω, t) := e

−

√

π cos



ωt



(9.38)

Fourier integral solution

> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−inﬁnity..inﬁnity);

u(x, t) :=

∞



−∞

−

cos



ωt



Iωx

√

dω (9.39)

> u(x,t):=invfourier(U(omega,t),omega,x);

u(x, t) := cosh(tx)e

−

−x

(9.40)

ANIMATION

> animate(u(x,t),x=−5..5,t=0..5,thickness=3);

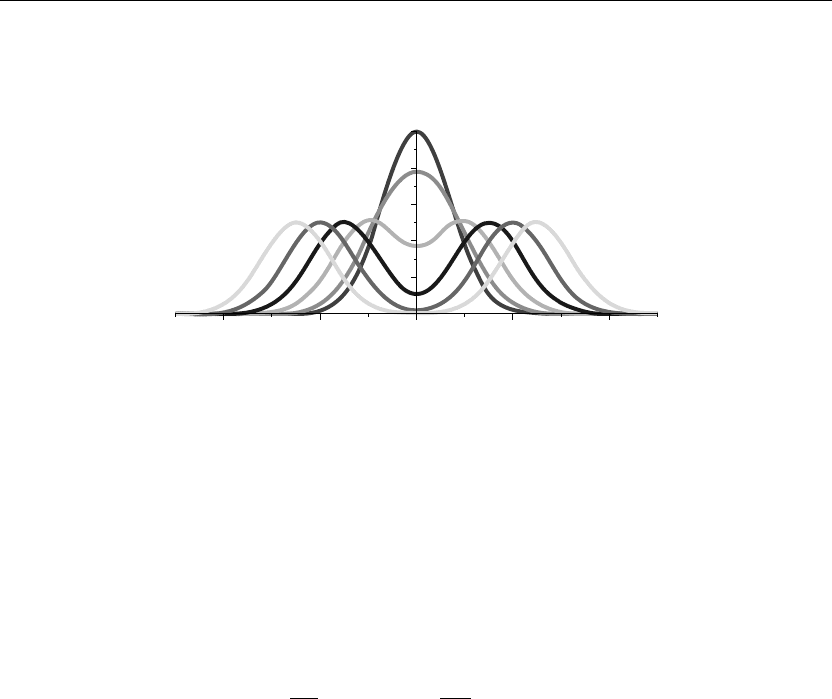
The preceding animation command shows the spatial-time-dependent solution of the wave

amplitude u(x, t). The animation sequence here and in Figure 9.5 shows snapshots of the

animation at times t = 0, 1, 2, 3, 4, 5.

ANIMATION SEQUENCE

> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):

> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):

596 Chapter 9

> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):

> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=−5..5,thickness=10);

0.2

0.4

0.6

0.8

242224

Figure 9.5

EXAMPLE 9.10.2: (Solution by method of images) We seek the wave amplitude u(x, t) for

transverse waves over a long string over the semi-inﬁnite interval I ={x |0 <x<∞}. The end

x = 0 is held ﬁxed. The initial displacement distribution u(x, 0) = f(x) is given as follows, and

the initial speed distribution u

(x, 0) = g(x) is 0. There are no external forces acting on the

system, and the wave speed is c = 1/2. We solve this problem using the method of images by

forming the odd extension of f(x) and using the regular Fourier integral.

SOLUTION: The wave partial differential equation is

∂

∂t

u(x, t) = c



∂

∂x

u(x, t)



The boundary conditions are that the solution be absolutely integrable over the interval and we

have a type 1 condition at x = 0:

∞



|u(x, t)|dx<∞ and u(0,t)= 0

The initial conditions are

u(x, 0) = xe

−x

and u

(x, 0) = 0

By the method of images, we use the Heaviside function H(x) to form the odd extension fo(x)

of f(x) with the operation

fo(x) = f(x)H(x) −f(−x)H(−x)

Inﬁnite and Semi-inﬁnite Spatial Domains 597

The Fourier integral form of the solution is

u(x, t) =

∞



−∞

U(ω, t) e

iωx

2π

dω

Here, U(ω, t) satisﬁes the differential equation

∂

∂t

U(ω, t) +c

U(ω, t) = 0

Assignment of system parameters

> restart:with(inttrans):with(plots):c:=1/2:f(x):=x*exp(−xˆ2):f(−x):=subs(x=−x,f(x)):g(x):=0:

g(−x):=subs(x=−x,g(x)):

Formation of the odd extension of f(x) and g(x)

> fo(x):=f(x)*Heaviside(x)−f(−x)*Heaviside(−x);

fo(x) := x e

−x

Heaviside(x) +x e

−x

Heaviside(−x) (9.41)

> go(x):=g(x)*Heaviside(x)−g(−x)*Heaviside(−x);

go(x) := 0 (9.42)

Fourier transform of initial conditions

> U(omega,0):=Int(fo(x)*exp(−I*omega*x),x=−inﬁnity..inﬁnity);

U(ω, 0) :=

∞



−∞



x e

−x

Heaviside(x) +x e

−x

Heaviside(−x)



−Iωx

dx (9.43)

> U(omega,0):=expand(fourier(f(x),x,omega));

U(ω, 0) := −

Iω e

−

√

π (9.44)

> V(omega,0):=Int(go(x)*exp(−I*omega*x),x=−inﬁnity..inﬁnity);V(omega,0):=value(%):

V(ω, 0) :=

∞



−∞

0dx (9.45)

> V(omega,0):=simplify(value(%));

V(ω, 0) := 0 (9.46)