Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


568 Chapter 9
9.5 Convolution Integral Solution for the
Diffusion Equation
We can rewrite the form of the earlier general solution in a manner that introduces the concept
of the convolution integral in addition to the initial and source value Green’s functions. We
break up the given solution into two parts. The first is due to the initial condition distribution
term f(x), and the second is due to the source term h(x, t). For the nonhomogeneous partial
differential equation, the general solution was shown earlier to be
u(x, t) =
∞
−∞
U(ω, 0) e
−kω
2
t
+
t
0
H(ω, τ) e
−kω
2
(t−τ)
dτ
e
iωx
2π
dω
This solution can be partitioned into two parts; that is, we can write
u(x, t) = u1(x, t) +u2(x, t)
where the first or initial condition part is
u1(x, t) =
∞
−∞
U(ω, 0) e
−kω
2
t
e
iωx
2π
dω
and the second or source term part is
u2(x, t) =
∞
−∞
t
0
H(ω, τ) e
−kω
2
(t−τ)
dτ
e
iωx
2π
dω
We focus on the initial condition term first. If we make the substitution
U(ω, 0) =
∞
−∞
f(s) e
−iωs
ds
into the first part of the solution, we get
u1(x, t) =
∞
−∞
⎛
⎝
∞
−∞
f(s) e
−iωs
2π
ds
⎞
⎠
e
−kω
2
t
e
iωx
dω
Interchanging the order of integration yields
u1(x, t) =
∞
−∞
f(s)
⎛
⎝
∞
−∞
e
−kω
2
t
e
iω(x−s)
2π
dω
⎞
⎠
ds

Infinite and Semi-infinite Spatial Domains 569
We recognize the inner integral as the shifted Fourier integral of the term
e
−kω
2
t
Evaluation of this Fourier integral yields what we call the “initial value Green’s function”
given here:
G1(x,t,s)=
e
−
(x−s)
2
4kt
2
√
πkt
Thus, we can write our initial value part of the solution as
u1(x, t) =
∞
−∞
f(s) e
−
(x−s)
2
4kt
2
√
πkt
ds
or, in terms of the initial value Green’s function, as
u1(x, t) =
∞
−∞
f(s) G1(x,t,s)ds
We now focus on the second part of the solution due to the source term. Making the substitution
H(ω, τ) =
∞
−∞
h(s, τ) e
−iωs
ds
into the second part yields
u2(x, t) =
∞
−∞
⎛
⎝
t
0
⎛
⎝
∞
−∞
h(s, τ) e
−iωs
2π
ds
⎞
⎠
e
−kω
2
(t−τ)
dτ
⎞
⎠
e
iωx
dω
Interchanging the order of integration yields
u2(x, t) =
t
0
∞
−∞
h(s, τ)
⎛
⎝
∞
−∞
e
−kω
2
(t−τ)
e
iω(x−s)
π
dω
⎞
⎠
ds dτ
Again, we recognize the inner integral as the shifted Fourier integral of the term
e
−kω
2
(t−τ)
Evaluating this integral yields what we call the “source value Green’s function” given here:
G2(x,t,s,τ)=
e
−
(x−s)
2
4k(t−τ)
2
√
πk(t −τ)

570 Chapter 9
Thus, we can write the second part of the solution as
u2(x, t) =
t
0
∞
−∞
e
−
(x−s)
2
4k(t−τ)
h(s, τ)
2
√
πk(t −τ)
ds dτ
or, in terms of the source value Green’s function, as
u2(x, t) =
t
0
∞
−∞
h(s,τ)G2(x,t,s,τ)ds dτ (9.2)
Combining the two parts gives us the final solution to the diffusion equation in the convolution
form:
u(x, t) =
∞
−∞
f(s) e
−
(x−s)
2
4kt
2
√
πkt
ds +
t
0
∞
−∞
e
−
(x−s)
2
4k(t−τ)
h(s, τ)
2
√
πk(t −τ)
ds dτ
We will use this convolution form of the solution in some of the example problems using
Maple later.
9.6 Nonhomogeneous Diffusion Equation over Semi-infinite
Domains
We now consider the same problem as earlier, but over the semi-infinite interval I ={x |0 <
x<∞}. We continue to assume that all functions are piecewise smooth and absolutely
integrable with respect to x over the semi-infinite interval. Depending on the boundary
condition at x = 0, we utilize those singular eigenfunctions that are consistent with the
boundary condition. We consider only homogeneous boundary conditions.
If, at x = 0, we have a type 1 boundary condition
u(0,t)= 0
then the appropriate (since they satisfy the type 1 boundary condition at the origin) singular
orthonormalized eigenfunctions are, from Section 9.3,
√
2 sin(ωx)
√
π
for 0 <ω<∞. Thus, we can write our solution in terms of these singular eigenfunctions as
u(x, t) =
∞
0
2U(ω, t) sin(ωx)
π
dω

Infinite and Semi-infinite Spatial Domains 571
From Section 9.3, we see that U(ω, t) is the time-dependent Fourier sine transform of u(x, t).
If we substitute the initial condition u(x, 0) = f(x) on this solution, we get
f(x) =
∞
0
2U(ω, 0) sin(ωx)
π
dω
Here, U(ω, 0) is the Fourier sine transform of the initial condition function f(x); that is,
U(ω, 0) =
∞
0
f(x) sin(ωx) dx (9.3)
In a similar manner, the source term h(x, t) can be expressed as the Fourier sine integral
h(x, t) =
∞
0
2H(ω, t) sin(ω x)
π
dω
where H(ω, t) is now the Fourier sine transform of h(x, t); that is,
H(ω, t) =
∞
0
h(x, t) sin(ωx) dx
Proceeding formally, as we did earlier, U(ω, t) satisfies the first-order differential equation
∂
∂t
U(ω, t) +kω
2
U(ω, t) = H(ω, t)
and the solution to this first-order initial value problem, from Section 1.3, is
U(ω, t) = U(ω, 0) e
−kω
2
t
+
t
0
H(ω, τ) e
−kω
2
(t−τ)
dτ
Thus, for the case of a semi-infinite interval with a type 1 condition at x = 0, the final solution
to our nonhomogeneous diffusion partial differential equation can be written as the Fourier sine
integral
u(x, t) =
∞
0
2
U(ω, 0) e
−kω
2
t
+
t
0
H(ω, τ) e
−kω
2
(t−τ)
dτ
sin(ωx)
π
dω
On the other hand, if, at x = 0, we have the type 2 condition
u
x
(0,t)= 0

572 Chapter 9
then the appropriate (since they satisfy the type 2 boundary condition at the origin) singular
orthonormalized eigenfunctions are, from Section 9.3,
√
2 cos(ωx)
√
π
for 0 <ω<∞. Thus, we can write our solution in terms of the singular eigenfunctions as
u(x, t) =
∞
0
2U(ω, t) cos(ωx)
π
dω
From Section 9.3, we see that U(ω, t) is the time-dependent Fourier cosine transform of u(x, t).
If we substitute the initial conditions into the solution, we get
f(x) =
∞
0
2U(ω, 0) cos(ωx)
π
dω
Here, U(ω, 0) is the Fourier cosine transform of the initial condition function f(x); that is,
U(ω, 0) =
∞
0
f(x) cos(ωx) dx
In a similar manner, the source term h(x, t) can be expressed as the Fourier cosine integral
h(x, t) =
∞
0
2H(ω, t) cos(ωx)
π
dω
where, H(ω, t) is now the Fourier cosine transform of h(x, t); that is,
H(ω, t) =
∞
0
h(x, t) cos(ωx) dx
Again, proceeding formally, as we did earlier, U(ω, t) satisfies the first-order differential
equation
∂
∂t
U(ω, t) +kω
2
U(ω, t) = H(ω, t)
and the solution to this first-order initial value problem, from Section 1.3, is
U(ω, t) = U(ω, 0) e
−kω
2
t
+
t
0
H(ω, τ) e
−kω
2
(t−τ)
dτ

Infinite and Semi-infinite Spatial Domains 573
Thus, for the case of a semi-infinite interval with a type 2 condition at x = 0, the final solution
to our nonhomogeneous diffusion partial differential equation can be written as the Fourier
cosine integral
u(x, t) =
∞
0
2
U(ω, 0) e
−kω
2
t
+
t
0
H(ω, τ) e
−kω
2
(t−τ)
dτ
cos(ωx)
π
dω
The Method of Images
In some cases involving semi-infinite domain problems with homogeneous boundary
conditions at the origin, it may be advantageous for us to employ what is called the “method of
images.” Depending on the boundary condition at the origin, we “reflect” the initial condition
function f(x) about the u-axis. For a problem with a type 1 condition at the origin, we simply
form the “odd” extension of f(x) and develop the rest of the solution using the regular Fourier
integral. Similarly, for a problem with a type 2 condition at the origin, we simply form the
“even” extension of f(x) and develop the rest of the solution using the regular Fourier integral.
We illustrate these techniques in some of the following examples.
9.7 Example Diffusion Problems over Infinite and
Semi-infinite Domains
We now use the procedures discussed to investigate solutions to heat and diffusion problems
over infinite and semi-infinite domains.
EXAMPLE 9.7.1: (Diffusion of a salt concentration) We consider a long, thin cylinder over the
infinite interval I ={x |−∞<x<∞} containing a fluid that initially has a salt concentration
density u(x, 0) = f(x) given as follows. We seek the density u(x, t) of the salt as it diffuses into
the fluid. The diffusivity of the medium is k = 1/4. There is no source term in the system.
Solve the problem by the Fourier transform method.
SOLUTION: The diffusion partial differential equation is
∂
∂t
u(x, t) = k
∂
2
∂x
2
u(x, t)
The boundary condition is that the solution be absolutely integrable over the interval; that is,
∞
−∞
|u(x, t)|dx<∞
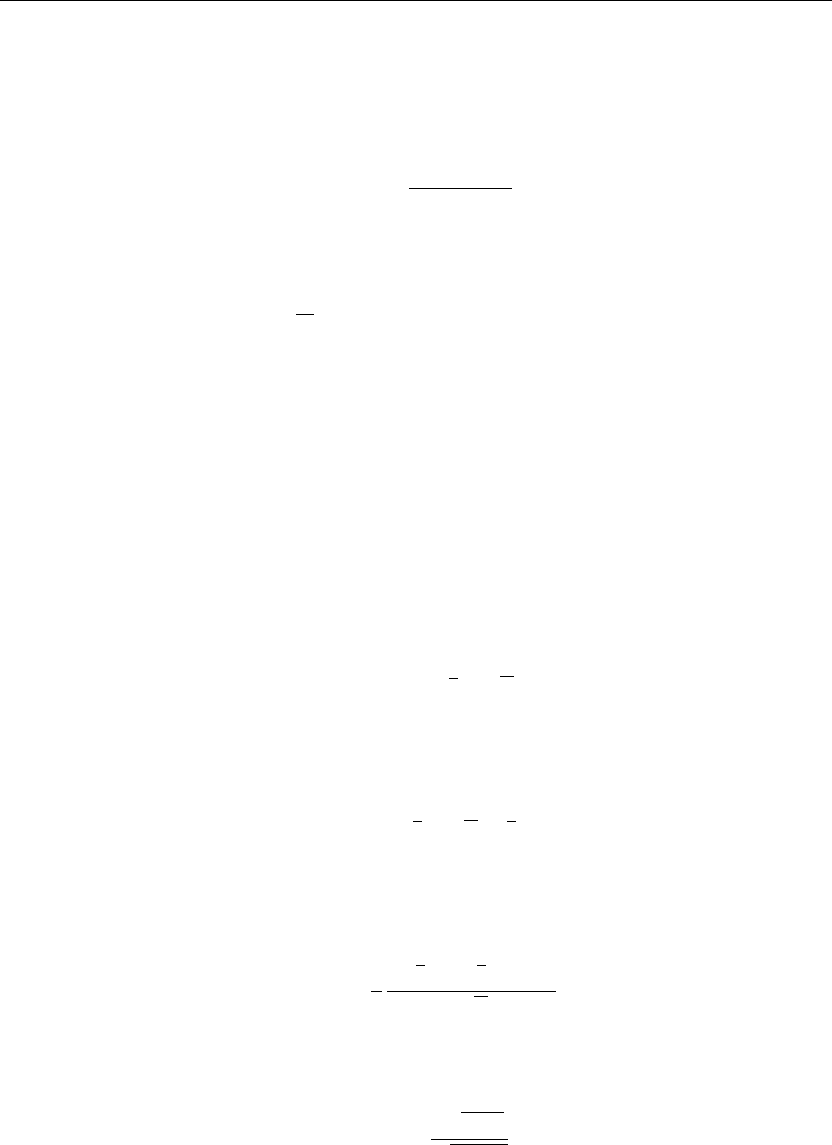
574 Chapter 9
The initial condition is
u(x, 0) = e
−x
2
The Fourier integral form of the solution is
u(x, t) =
∞
−∞
U(ω, t) e
iωx
2π
dω
Here, U(ω, t) satisfies the differential equation
∂
∂t
U(ω, t) +kω
2
U(ω, t) = 0
Assignment of system parameters
> restart:with(plots):k:=1/4:f(x):=exp(−xˆ2):
Fourier transform of initial condition term
> U(omega,0):=Int(f(x)*exp(−I*omega*x),x=−infinity..infinity);U(omega,0):=value(%):
U(ω, 0) :=
∞
−∞
e
−x
2
e
−Iωx
dx (9.4)
> U(omega,0):=simplify(value(%));
U(ω, 0) := e
−
1
4
ω
2
√
π (9.5)
Fourier transform of solution
> U(omega,t):=U(omega,0)*exp(−k*omegaˆ2*t);
U(ω, t) := e
−
1
4
ω
2
√
π e
−
1
4
ω
2
t
(9.6)
Fourier integral solution
> u(x,t):=Int(U(omega,t)/(2*Pi)*exp(I*omega*x),omega=−infinity..infinity);assume(t>0):
u(x, t) :=
∞
−∞
1
2
e
−
1
4
ω
2
e
−
1
4
ω
2
t
e
Iωx
√
π
dω (9.7)
> u(x,t):=simplify(value(%));
u(x, t∼) :=
e
−
x
2
1+t∼
√
1 +t∼
(9.8)
Infinite and Semi-infinite Spatial Domains 575
ANIMATION
> animate(u(x,t),x=−5..5,t=0..5,thickness=3);
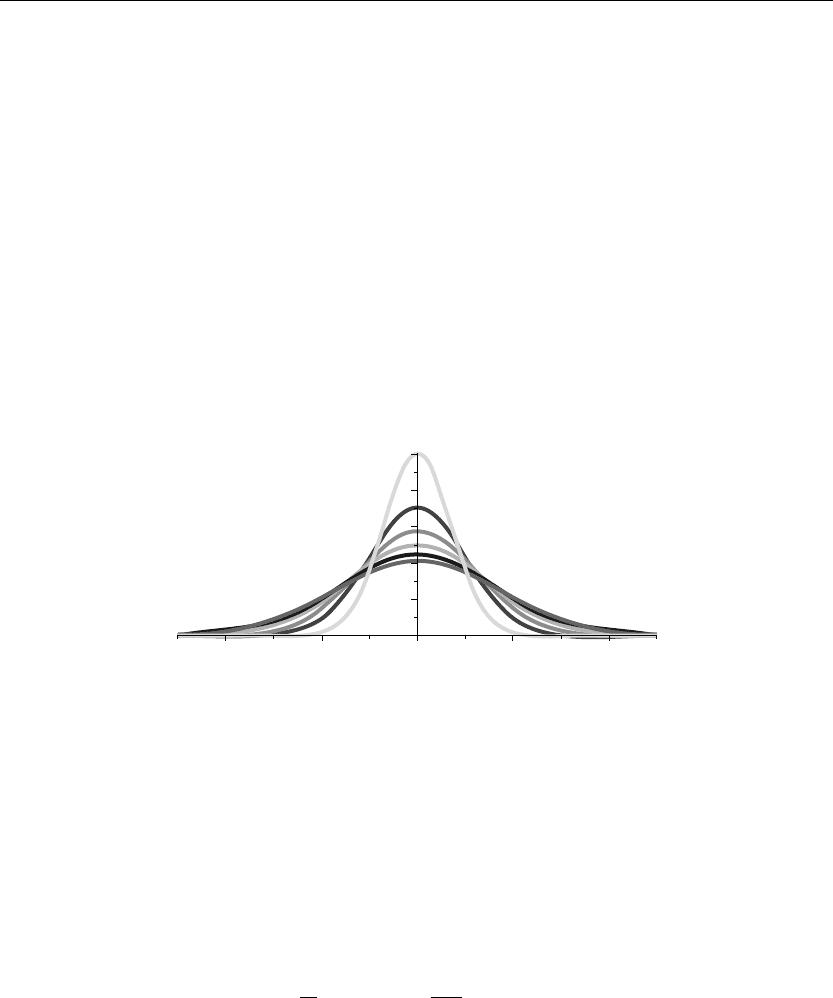
The preceding animation command shows the spatial-time-dependent solution of the density
u(x, t) in the medium. The animation sequence here and in Figure 9.1 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=−5..5,thickness=10);
24 220
x
0.2
0.4
0.6
0.8
1
24
Figure 9.1
EXAMPLE 9.7.2: (Solution by convolution) We consider a long, thin cylinder over the infinite
interval I ={x |−∞<x<∞} containing a fluid that initially has a salt concentration density
u(x, 0) = f(x) given as follows. We seek the density u(x, t) of the salt as it diffuses into the
fluid. The diffusivity of the medium is k = 1/4. There is no source term in the system. This is
the same problem as the preceding, but we now develop the solution using the method of
convolution.
SOLUTION: The diffusion partial differential equation is
∂
∂t
u(x, t) = k
∂
2
∂x
2
u(x, t)
The boundary condition is that the solution be absolutely integrable over the interval; that is,
∞
−∞
|u(x, t)|dx<∞

576 Chapter 9
The initial condition is
u(x, 0) = e
−x
2
The convolution form of the solution, from Section 9.5 for no internal source, is
u(x, t) =
∞
−∞
f(s) e
−
(x−s)
2
4kt
2
√
πkt
ds
Assignment of system parameters
> restart:with(plots):k:=1/4:f(x):=exp(−xˆ2):f(s):=subs(x=s,f(x)):
Convolution of the initial condition contribution
> u(x,t):=Int(f(s)*exp(−(x−s)ˆ2/(4*k*t))/(2*sqrt(Pi*k*t)),s=−infinity..infinity);assume(t>0):
u(x, t) :=
∞
−∞
e
−s
2
e
−
(x−s)
2
t
√
πt
ds (9.9)
Convolution solution
> u(x,t):=simplify(value(%));
u(x, t ∼) :=
e
−
x
2
t∼+1
√
t∼+1
(9.10)
Comparing our solution with Example 9.7.1, we arrive at the same answer by either the
transform method or the convolution method.
EXAMPLE 9.7.3: (The error function solution) We seek the temperature distribution u(x, t) in
a thin, long rod over the infinite interval I ={x |−∞<x<∞} whose lateral surface is
insulated. The initial temperature distribution u(x, 0) = f(x) is given as follows. There is no
source term in the system, and the thermal diffusivity is k = 1/2.
SOLUTION: The diffusion partial differential equation is
∂
∂t
u(x, t) = k
∂
2
∂x∂x
u
[]
(x, t)
The boundary condition is that the solution be absolutely integrable over the interval; that is,
∞
−∞
|u(x, t)|dx<∞

Infinite and Semi-infinite Spatial Domains 577
The initial condition is
u(x, 0) = H(x)
where H(x) is the Heaviside function.
The convolution form of the solution, from Section 9.5 for no internal source, is
u(x, t) =
∞
−∞
f(s) e
−
(x−s)
2
4kt
2
√
πkt
ds
Assignment of system parameters
> restart:with(plots):k:=1/2:f(x):=Heaviside(x):f(s):=subs(x=s,f(x)):assume(t>0):
Convolution of the initial condition contribution
> u(x,t):=Int(f(s)*exp(−(x−s)ˆ2/(4*k*t))/(2*sqrt(Pi*k*t)),s=−infinity..infinity);
u(x, t∼) :=
∞
−∞
1
2
Heaviside(s) e
−
1
2
(x−s)
2
t∼
√
2
√
πt∼
ds (9.11)
Convolution solution
> u(x,t):=simplify(value(%));
u(x, t∼) :=
1
2
erf
1
2
x
√
2
√
t∼
+
1
2
(9.12)
where the erf (x) term denotes the error function.
ANIMATION
> animate(u(x,t),x=−5..5,t=1/100..5,thickness=3);
The preceding animation command shows the spatial-time-dependent solution of the
temperature u(x, t) in the medium. The animation sequence here and in Figure 9.2 shows
snapshots of the animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=1/1000,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)}x=−5..5,thickness=10);
