Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


538 Chapter 8
> D(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},D(n)));
D(n) :=
40
√
2(−1)
n
π
3
8n
3
−12n
2
+6n −1
(8.155)
for n = 1, 2, 3,....
Final solution (linear plus variable portion)
> u(x,t):=Sum(eval(v[n](x,t)),n=1..infinity)+s(x,t);
u(x, t) :=
∞
n=1
⎛
⎝
8
√
2 cos
1
10
(2n −1)πt
π
3
8n
3
−12n
2
+6n −1
+
40
√
2(−1)
n
sin
1
10
(2n −1)πt
π
3
8n
3
−12n
2
+6n −1
+
400(−1)
1+n
2 sin(t) −10 sin
1
5
πnt
cos
1
10
πt
√
2
16n
4
π
2
−32n
3
π
2
+24π
2
n
2
−8π
2
n +π
2
−400n
2
+400n −100
(2n −1)π
3
×
√
2 sin
1
2
(2n −1)πx
+sin(t)x (8.156)
First few terms of sum
> u(x,t):=sum(eval(v[n](x,t)),n=1..3)+s(x,t):
ANIMATION
> animate(u(x,t),x=0..a,t=0..5,thickness=3);
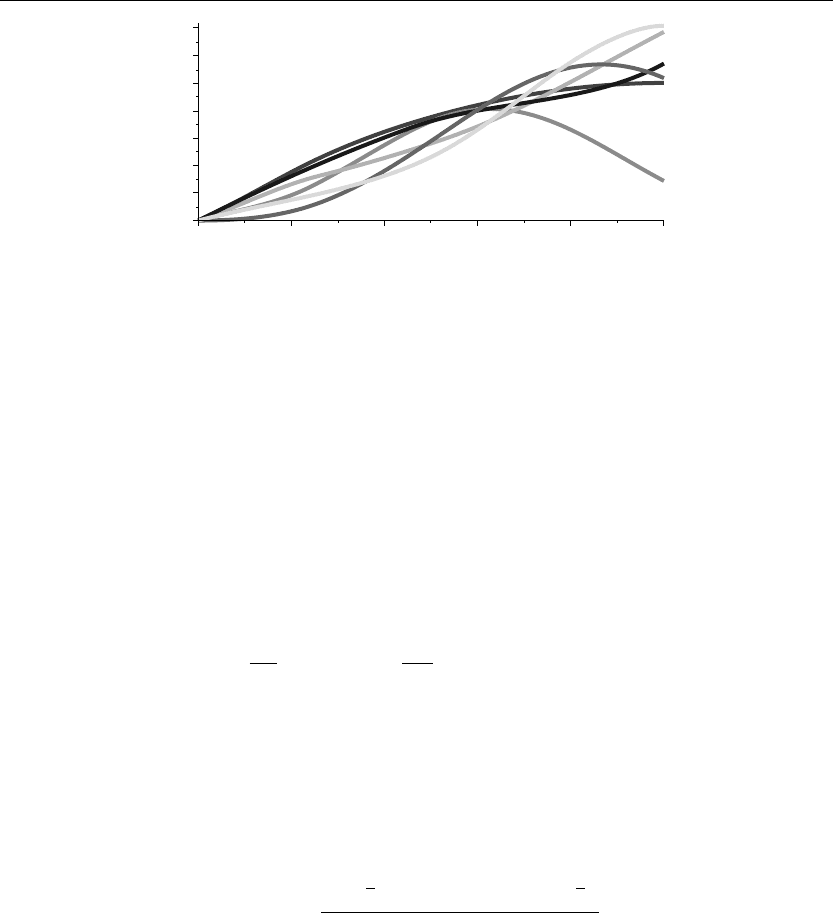
The preceding animation command displays the spatial-time-dependent solution of u(x, t) for
the given boundary conditions and initial conditions. The animation sequence here and in
Figure 8.8 shows snapshots of the animation at times t = 0, 1, 2, 3, 4, 5. Note how the solution
satisfies the given boundary and initial conditions.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..a,thickness=10);
Nonhomogeneous Partial Differential Equations 539
0.2
0
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.4 0.6 0.8 1
x
Figure 8.8
EXAMPLE 8.7.4: (Resonance on a plucked magnetic wire) We again consider transverse
wave motion along the same taut magnetic wire as discussed in Example 8.7.2. Both ends of
the wire are held fixed. An external applied magnetic force acts on the wire. The wire has an
initial displacement distribution f(x), corresponding to that of a wire plucked at the center, and
an initial speed distribution g(x). The external force term h(x, t) acting upon the wire has a
center-symmetric x dependence and a sinusoidal time dependence (angular frequency equals
ω), which matches a natural vibration frequency within the system, thus producing resonance.
There is no damping in the system and the wave speed is c = 1.
SOLUTION: The nonhomogeneous wave equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
+h(x, t)
The boundary conditions are homogeneous type 1 at the left and homogeneous type 1 at the
right:
u(0,t)= 0 and u(1,t)= 0
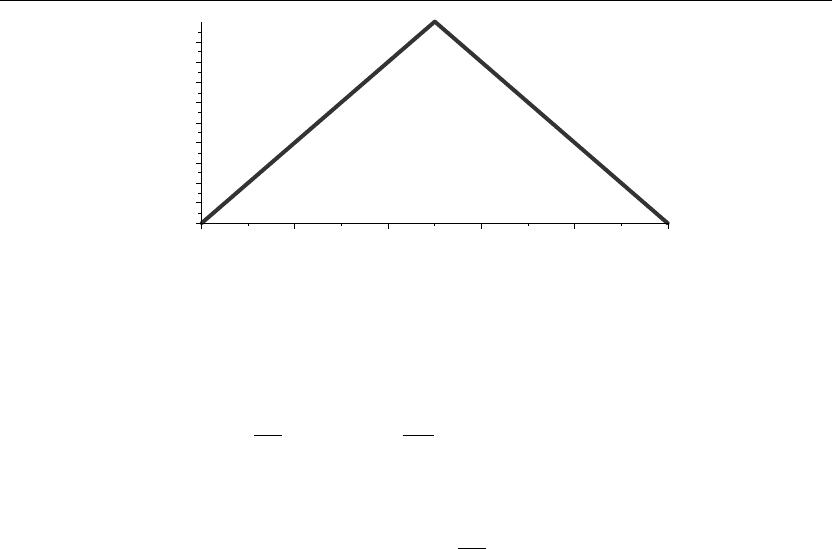
The initial displacement distribution is that of a center-plucked wire
u(x, 0) =
xH
1
2
−x
+(1 −x)H
x −
1
2
5
where H(x) denotes the Heaviside function. Recall the Heaviside function H(x) has the value 1
for 0 <xand the value 0 for x<0. A plot of this initial displacement is shown in Figure 8.9.
The initial speed distribution is
u
t
(x, 0) = 0
and the external applied force is
h(x, t) = 10 x(1 −x) cos(ω t)
540 Chapter 8
0.20
0
0.02
0.04
0.06
0.09
0.4 0.6 0.8 1
x
Figure 8.9
The solution is u(x, t) = v(x, t) +s(x, t), where s(x, t) is the linear portion of the solution and
v(x, t) is the variable portion of the solution that satisfies the partial differential equation
∂
2
∂t
2
v(x, t) = c
2
∂
2
∂x
2
v(x, t)
+q(x, t)
where
q(x, t) = h(x, t) −
∂
2
∂t
2
s(x, t)
Assignment of system parameters
> restart:with(plots):a:=1:c:=1:h(x,t):=10*x*(1−x)*cos(omega*t):
> A(t):=0:B(t):=0:kappa[1]:=1:kappa[2]:=0:kappa[3]:=1:kappa[4]:=0:
> b(t):=(kappa[3]*a*A(t)+A(t)*kappa[4]−B(t)*kappa[2])/(kappa[1]*kappa[3]*a+kappa[1]*
kappa[4]−kappa[2]*kappa[3]);
b(t) := 0 (8.157)
> m(t):=(kappa[1]*B(t)−A(t)*kappa[3])/(kappa[1]*kappa[3]*a+kappa[1]*kappa[4]
−kappa[2]*kappa[3]);
m(t) := 0 (8.158)
Linear portion of solution
> s(x,t):=m(t)*x+b(t);s(x,0):=eval(subs(t=0,s(x,t))):s[t](x,0):=eval(subs(t=0,diff(s(x,t),t))):
s(x, t) := 0 (8.159)
By the method of separation of variables, the variable solution is
v(x, t) =
∞
n=0
X
n
(x)T
n
(t)

Nonhomogeneous Partial Differential Equations 541
where T
n
(t) is the solution to the time-dependent differential equation
d
2
dt
2
T
n
(t) +c
2
λ
n
T
n
(t) = Q
n
(t)
and X
n
(x) is the solution to the spatial-dependent eigenvalue equation
d
2
dx
2
X
n
(x) +λ
n
X
n
(x) = 0
with boundary conditions
X(0) = 0 and X(1) = 0
The corresponding homogeneous eigenfunction problem consists of the Euler equation, along
with the homogeneous boundary conditions that are type 1 at the left and type 1 at the right.
The allowed eigenvalues and corresponding orthonormal eigenfunctions, obtained from
Example 2.5.1, are
> lambda[n]:=(n*Pi/a)ˆ2;
λ
n
:= n
2
π
2
(8.160)
> X[n](x):=sqrt(2/a)*sin(n*Pi/a*x);X[m](x):=subs(n=m,X[n](x)):
X
n
(x) :=
√
2 sin(nπx) (8.161)
for n = 1, 2, 3,....
Statement of orthonormality with the respective weight function w(x) = 1
> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=0..a)=delta(n,m);
1
0
2 sin(nπx) sin(mπx)dx = δ(n, m) (8.162)
Time-dependent equation
> diff(T[n](t),t,t)+cˆ2*lambda[n]*T[n](t)=Q[n](t);
d
2
dt
2
T
n
(t) +n
2
π
2
T
n
(t) = Q
n
(t) (8.163)
> q(x,t):=h(x,t)−diff(s(x,t),t,t);
q(x, t) := 10x(1 −x) cos(ωt) (8.164)
> Q[n](t):=Int(q(x,t)*X[n](x),x=0..a);Q[n](t):=expand(value(%)):
Q
n
(t) :=
1
0
10x(1 −x) cos(ωt)
√
2 sin(nπx) dx (8.165)

542 Chapter 8
> Q[n](t):=simplify(factor(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},Q[n](t))));Q[n](tau):=
subs(t=tau,%):
Q
n
(t) := −
20 cos(ωt)
√
2
−1 +(−1)
n
n
3
π
3
(8.166)
Basis vectors
> T1(t):=cos(c*n*Pi*t/a);
T 1(t) := cos(nπt) (8.167)
> T2(t):=sin(c*n*Pi*t/a);
T 2(t) := sin(nπt) (8.168)
Second-order Green’s function
> G2(t,tau):=sin(c*n*Pi/a*(t−tau))/(c*n*Pi/a);
G2(t, τ) :=
sin(nπ(t −τ))
nπ
(8.169)
Time-dependent solution
> T[n](t):=C(n)*T1(t)+D(n)*T2(t)+Int(G2(t,tau)*Q[n](tau),tau=0..t);
T
n
(t) := C(n) cos(nπt) +D(n) sin(nπt) +
t
0
−
20 sin(nπ(t −τ)) cos(ωτ)
√
2
−1 +(−1)
n
n
4
π
4
dτ
(8.170)
> T[n](t):=value(%);v[n](x,t):=(T[n](t)*X[n](x)):
T
n
(t) := C(n) cos(nπt) +D(n) sin(nπt) −
20
√
2
−1 +(−1)
n
(
−cos(nπt) +cos(ωt)
)
n
3
π
3
n
2
π
2
−ω
2
(8.171)
Variable portion of solution
> v(x,t):=Sum(v[n](x,t),n=1..infinity);
v(x, t) :=
∞
n=1
C(n) cos(nπt) +D(n) sin(nπt) (8.172)
−
20
√
2
−1 +(−1)
n
(
−cos(nπt) +cos(ωt)
)
n
3
π
3
n
2
π
2
−ω
2
√
2 sin(nπx)

Nonhomogeneous Partial Differential Equations 543
The Fourier coefficients C(n) and D(n) are to be determined from the initial conditions on
v(x, t). We now substitute the initial conditions v(x, 0) = f(x) −s(x, 0) and
v
t
(x, 0) = g(x) −s
t
(x, 0) into the integrals for C(n) and D(n) for the special case where
> f(x):=1/5*(x*Heaviside(1/2−x)+(1−x)*Heaviside(x−1/2));
f(x) :=
1
5
x Heaviside
1
2
−x
+
1
5
(1 −x) Heaviside
x −
1
2
(8.173)
> g(x):=0;
g(x) := 0 (8.174)
The integrals for C(n) and D(n) are
> C(n):=Int((f(x)−s(x,0))*X[n](x),x=0..a);C(n):=expand(value(%)):
C(n) :=
1
0
1
5
x Heaviside
1
2
−x
+
1
5
(1 −x) Heaviside
x −
1
2
√
2 sin(nπx) dx
(8.175)
> C(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},C(n)));
C(n) :=
2
5
√
2 sin
1
2
nπ
n
2
π
2
(8.176)
> D(n):=Int((g(x)−s[t](x,0))/(c*n*Pi/a)*X[n](x),x=0..a);D(n):=expand(value(%)):
D(n) :=
1
0
0dx (8.177)
> D(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},D(n)));
D(n) := 0 (8.178)
for n = 1, 2, 3,....
Final solution (linear plus variable portion)
> u(x,t):=Sum(eval(v[n](x,t)),n=1..infinity)+s(x,t);
u(x, t) :=
∞
n=1
⎛
⎝
2
5
√
2 sin
1
2
nπ
cos(nπt)
n
2
π
2
−
20
√
2
−1 +(−1)
n
(
−cos(nπt) +cos(ωt)
)
n
3
π
3
n
2
π
2
−ω
2
√
2 sin(nπx) (8.179)
544 Chapter 8
The Special Case for Resonance in the System
To demonstrate resonance, we consider the special case where the source angular frequency
(ω) is identical to one of the natural vibration frequencies of the system—that is, the case
where ω = 3 π. We set
> omega:=3*Pi;
ω := 3π (8.180)
From the earlier solution, note that several terms in the denominator equal 0 for n = 3 when
ω = 3 π; this is a condition that gives rise to resonance in the system at that particular
frequency. In the evaluation of the preceding sum in the solution for u(x, t), we encounter a
numerical problem because of the vanishing of these denominator terms. To evaluate the
special term when n = 3, we must use l’Hopital’s rule, which takes a limit on the term. We
make a separate evaluation of the limit for the n = 3 term, T
3
(t):
> T[3](t):=limit(eval(T[n](t)),n=3);v[3](x,t):=T[3](t)*subs(n=3,X[n](x)):
T
3
(t) :=
1
405
400
√
2t sin(πt) cos(πt)
2
−100
√
2t sin(πt) −72
√
2 cos(πt)
3
π
2
+54
√
2 cos(πt)π
2
π
4
(8.181)
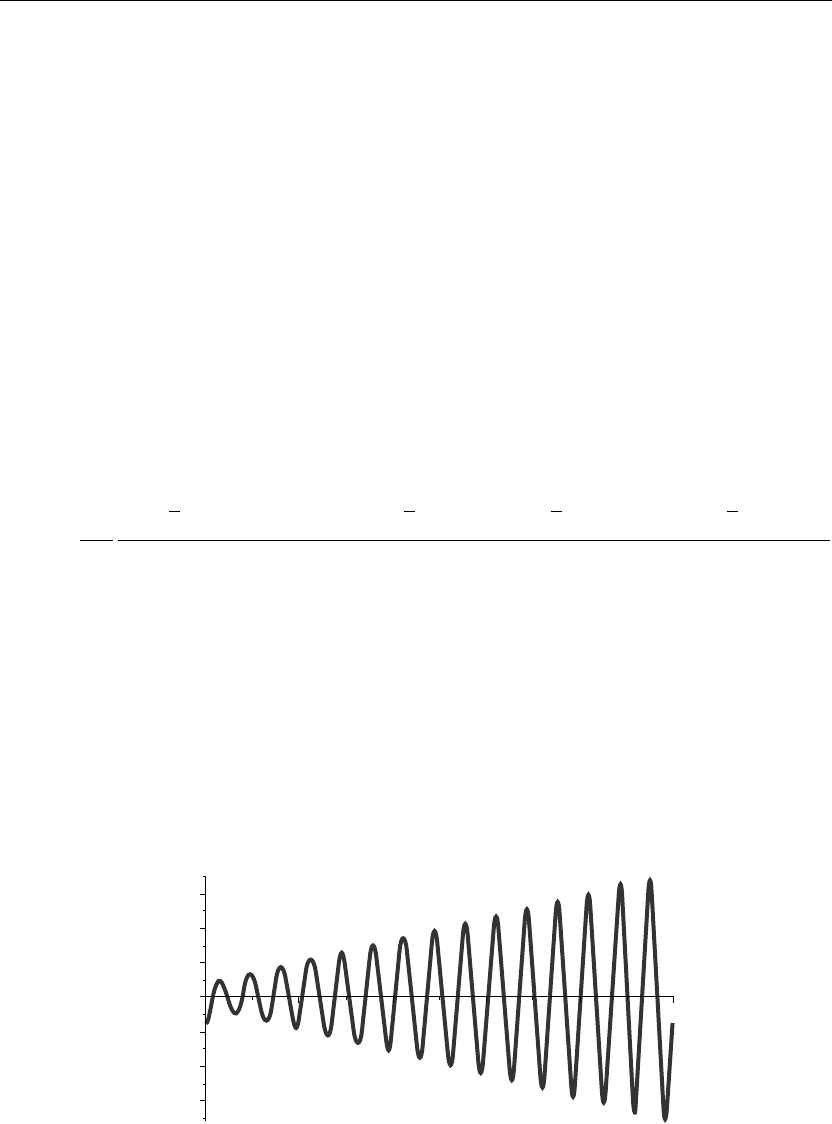
Note that the T
3
(t) term has components that increase linearly with time. This is due to the
fact that we are driving the wire with a force whose frequency dependence is identical to the
natural vibration frequency of the n = 3 mode. We plot the T
3
(t) term in Figure 8.10, and we
see the linear increase in time of the amplitude of this particular component of the Fourier
series expansion. This increase in amplitude is the manifestation of what is called
“resonance.”
> plot(T[3](t),t=0..10,thickness=3);
2
20.03
20.02
20.01
0
0.01
0.02
0.03
46810
t
Figure 8.10

Nonhomogeneous Partial Differential Equations 545
Final solution (particular plus linear portion) demonstrating resonance
> u(x,t):=eval(v(x,t))+s(x,t);
u(x, t) :=
∞
n=1
⎛
⎝
2
5
√
2 sin
1
2
nπ
cos(nπt)
n
2
π
2
−
20
√
2(−1 +(−1)
n
)
(
−cos(nπt) +cos(3πt)
)
n
3
π
3
n
2
π
2
−9π
2
√
2 sin(nπx) (8.182)
First few terms of sum
> u(x,t):=s(x,t)+sum(eval(v[n](x,t)),n=1..2)+v[3](x,t):
ANIMATION
> animate(u(x,t),x=0..a,t=0..50,frames=50,thickness=3);
The preceding animation command displays the spatial-time-dependent solution of u(x, t) for
the given boundary conditions and initial conditions. The animation sequence here and in
Figure 8.11 shows snapshots of the animation at times t = 0, 10/4, 20/4, 30/4, 40/4, 50/4. As
time increases, the n = 3 term dominates the solution to the problem, and this is why we see
three antinodes in the display of the wave amplitude.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,10/4):=subs(t=10/4,u(x,t)):
> u(x,20/4):=subs(t=20/4,u(x,t)):u(x,30/4):=subs(t=30/4,u(x,t)):
> u(x,40/4):=subs(t=40/4,u(x,t)):u(x,50/4):=subs(t=50/4,u(x,t)):
> plot({u(x,0),u(x,10/4),u(x,20/4),u(x,30/4),u(x,40/4),u(x,50/4)},x=0..a,thickness=10);
0.2
0.08
0.06
0.04
0.02
20.02
20.04
20.06
20.08
0
0.4 0.6
0.8
1
x
Figure 8.11

546 Chapter 8
Chapter Summary
The nonhomogeneous diffusion or heat equation
∂
∂t
u(x, t) = k
∂
2
∂x
2
u(x, t)
+h(x, t)
The nonhomogeneous boundary conditions
κ
1
u(0,t)+κ
2
u
x
(0,t)= A(t)
and
κ
3
u(a, t) +κ
4
u
x
(a, t) = B(t)
Linear (equilibrium) portion of solution
s(x, t) = m(t)x +b(t)
First-order Green’s function
G1(t, τ) = e
−λ
n
k(t−τ)
Transient solution
v(x, t) =
∞
n=0
⎛
⎝
C(n)e
−kλ
n
t
+
t
0
G1(t, τ)Q
n
(τ) dτ
⎞
⎠
X
n
(x)
Final solution for the diffusion equation (variable plus linear portion)
u(x, t) =
∞
n=0
⎛
⎝
C(n) e
−kλ
n
t
+
t
0
G1(t, τ)Q
n
(τ) dτ
⎞
⎠
X
n
(x) +m(t)x +b(t)
The nonhomogeneous wave equation
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t) +h(x, t)
Nonhomogeneous boundary conditions
κ
1
u(0,t)+κ
2
u
x
(0,t)= A(t)
and
κ
3
u(a, t) +κ
4
u
x
(a, t) = B(t)

Nonhomogeneous Partial Differential Equations 547
General solution
u(x, t) = v(x, t) +s(x, t)
Linear portion of the solution
s(x, t) = m(t)x +b(t)
Second-order Green’s function
G2(t, τ) =
sin
c
√
λ
n
(t −τ)
c
√
λ
n
Particular solution
v(x, t) =
∞
n=0
⎛
⎝
C(n) cos
c
λ
n
t
+D(n)sin
c
λ
n
t
+
t
0
G2(t, τ)Q
n
(τ) dτ
⎞
⎠
X
n
(x)
Final solution for the nonhomogeneous wave equation (particular plus linear portion)
u(x, t) =
∞
n=0
⎛
⎝
C(n) cos
c
λ
n
t
+D(n) sin
c
λ
n
t
+
t
0
G2(t, τ)Q
n
(τ) dτ
⎞
⎠
X
n
(x) +m(t)x +b(t)
In this chapter, we examined the nonhomogeneous equivalents to the diffusion and wave
equations discussed in Chapters 3 and 4. The partial differential equations were
nonhomogeneous either because of the presence of a driving term or because of the presence
of a nonhomogeneous boundary condition. The solutions were resolved by breaking up the
problem into two portions: a linear (equilibrium) portion and a variable (particular) portion.
Using the method of eigenfunction expansions, we were able to obtain final solutions to the
nonhomogeneous problem.
Exercises
We consider problems for nonhomogeneous diffusion and wave equations in the rectangular
coordinate system in a single dimension. The problems are nonhomogeneous either
because there is an external source acting on the system or the boundary conditions are
nonhomogeneous, or both of these reasons. Use the method of separation of variables and
eigenfunction expansions to evaluate the solutions.
