Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

508 Chapter 8

> lambda[n]:=(n*Pi/a)ˆ2;

:= n

(8.70)

> X[n](x):=sqrt(2/a)*sin(n*Pi/a*x);X[m](x):=subs(n=m,X[n](x)):

(x) :=

√

2 sin(nπx) (8.71)

for n = 1, 2, 3,....

Statement of orthonormality with the respective weight function w(x) = 1

> w(x):=1:Int(X[n](x)*X[m](x)*w(x),x=0..a)=delta(n,m);



2 sin(nπx) sin(mπx) dx = δ(n, m) (8.72)

Time-dependent equation

> diff(T[n](t),t)+k*lambda[n]*T[n](t)=Q[n](t);

(t) +

(t) = Q

(t) (8.73)

> q(x,t):=h(x,t)−diff(s(x,t),t);

q(x, t) := xt (8.74)

> Q[n](t):=Int(q(x,t)*X[n](x),x=0..a);Q[n](t):=expand(value(%)):

(t) :=



√

2 sin(nπx) dx (8.75)

> Q[n](t):=simplify(factor(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},Q[n](t))));

Q[n](tau):=subs(t=tau,%):

(t) := −

√

2(−1)

nπ

(8.76)

Basis vector

> T1(t):=exp(−k*lambda[n]*t);

T 1(t) := e

−

(8.77)

First-order Green’s function

> G1(t,tau):=simplify(T1(t)/(subs(t=tau,T1(t))));

G1(t, τ) := e

−

(t−τ)

(8.78)

Nonhomogeneous Partial Differential Equations 509

Time-dependent solution

> T[n](t):=eval(C(n)*T1(t)+Int(G1(t,tau)*Q[n](tau),tau=0..t));

(t) := C(n) e

−



⎛

⎝

−

(

t−τ

)

√

2(−1)

nπ

⎞

⎠

dτ (8.79)

> T[n](t):=value(%);v[n](x,t):=simplify(eval(T[n](t)*X[n](x))):

(t) := C(n) e

−

40(−1)

1+n

√



40 e

−

−40 +n



(8.80)

Variable portion of solution

> v(x,t):=Sum(v[n](x,t),n=1..inﬁnity);

v(x, t) :=

∞



n=1



C(n)e

−

+1600(−1)

1+n

−

√

+1600

√

2(−1)

+40(−1)

1+n

√

2 n



√

2 sin(nπx)



(8.81)

The Fourier coefﬁcients C(n) are determined from the integral in Section 8.3 for the special

case where

> f(x):=0;

f(x) := 0 (8.82)

> C(n):=Int((f(x)−s(x,0))*X[n](x),x=0..a);C(n):=expand(value(%)):

C(n) :=



0dx (8.83)

> C(n):=simplify(subs({sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},C(n)));

C(n) := 0 (8.84)

for n = 1, 2, 3,...,

> T[n](t):=(C(n)*T1(t)+int(G1(t,tau)*Q[n](tau),tau=0..t)):v[n](x,t):=(T[n](t)*X[n](x)):

Final solution (linear plus variable portion)

> u(x,t):=eval(Sum(v[n](x,t),n=1..inﬁnity)+s(x,t));

u(x, t) :=

∞



n=1

80(−1)

1+n



40 e

−

−40 +n



sin(nπx)

(8.85)

510 Chapter 8

First few terms of sum

> u(x,t):=s(x,t)+sum(v[n](x,t),n=1..3):

ANIMATION

> animate(u(x,t),x=0..a,t=0..5,thickness=3);

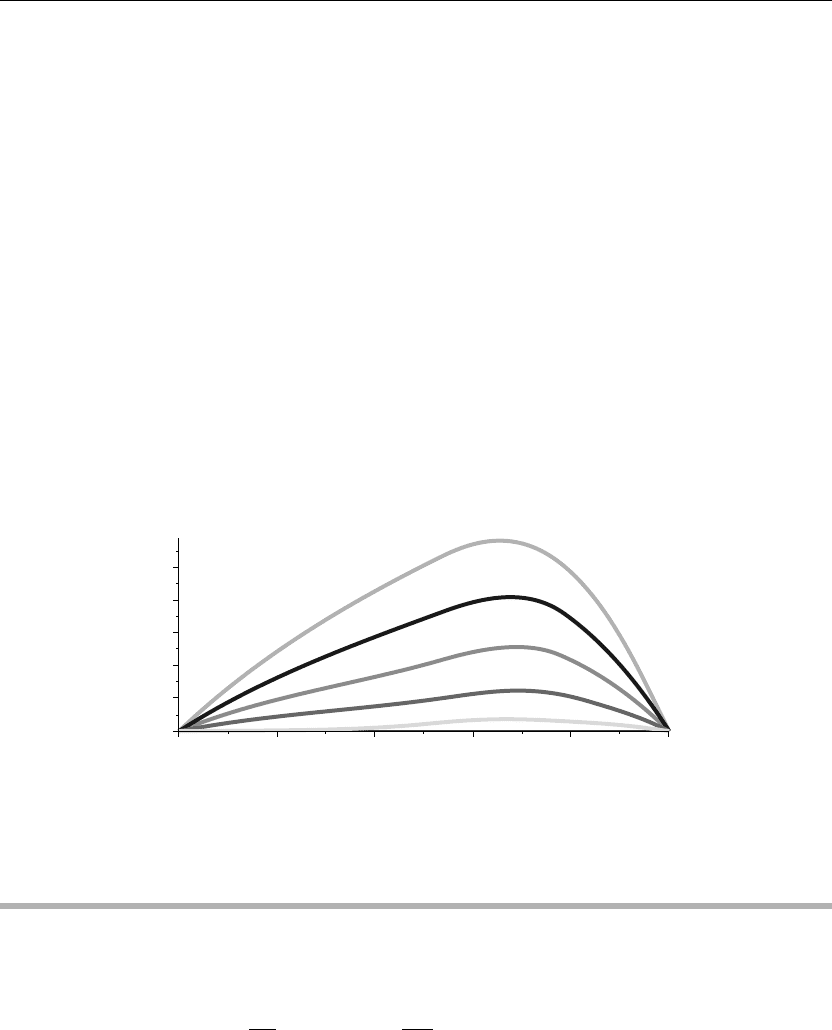
The preceding animation command displays the spatial-time-dependent solution of u(x, t) for

the given boundary conditions and initial conditions. The animation sequence here and in

Figure 8.5 shows snapshots of the animation at times t = 0, 1, 2, 3, 4, 5. Note how the solution

satisﬁes the given boundary and initial conditions.

ANIMATION SEQUENCE

> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):

> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):

> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):

> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..a,thickness=10);

0 0.2 0.4 0.6 0.8 1

Figure 8.5

8.5 Nonhomogeneous Wave Equation

The generalized nonhomogeneous wave partial differential equation in one dimension over the

ﬁnite interval I ={x |0 <x<a}, with no damping in the system, has the form

∂

∂t

u(x, t) = c



∂

∂x

u(x, t)



+h(x, t)

Here, u(x, t) denotes the wave amplitude with dimensions of distance, c is the wave speed with

dimensions of distance per time, and h(x, t), with dimensions of force per mass, now accounts

Nonhomogeneous Partial Differential Equations 511

for any external forces acting on the system. We consider this partial differential equation

along with the time-dependent nonhomogeneous boundary conditions

u(0,t)+κ

(0,t)= A(t)

and

u(a, t) +κ

(a, t) = B(t)

where A(t) and B(t) are the time-dependent nonhomogeneous source terms at the boundaries

of the domain. We seek a solution to this problem subject to satisfying the following two initial

conditions:

u(x, 0) = f(x)

and

(x, 0) = g(x)

Here, u(x, t) = f(x) denotes the initial amplitude distribution of the wave, and u

(x, 0) = g(x)

denotes the initial speed distribution of the wave.

Similar to what we did earlier for the diffusion equation, the solution procedure is driven by

our need to ﬁnd a complete set of orthonormal eigenfunctions corresponding to the equivalent

set of homogeneous boundary conditions over the given domain. To move in this direction, we

use the superposition principle, and we assume our solution to have the form

u(x, t) = v(x, t) +s(x, t)

For the types of boundary conditions we will be considering, s(x, t) will continue to have the

form of a “linear” solution and v(x, t) will have the form of a “variable” solution. Substituting

the preceding assumed solution into the partial differential equation yields

∂

∂t

v(x, t) +

∂

∂t

s(x, t) = c



∂

∂x

v(x, t) +

∂

∂x

s(x, t)



+h(x, t)

Doing the same with the boundary conditions, we get

A(t) = κ

v(0,t)+κ

(0,t)+κ

s(0,t)+κ

(0,t)

and

B(t) = κ

v(a, t) +κ

(a, t) +κ

s(a, t) +κ

(a, t)

Similarly, for the two initial conditions, we have

f(x) = v(x, 0) +s(x, 0)

512 Chapter 8

and

g(x) = v

(x, 0) +s

(x, 0)

As we did with the diffusion equation, our goal now is to substitute the conditions on the

solutions v(x, t) and s(x, t) so

1. s(x, t) (steady-state portion) will be a linear function of x; thus, the second-order partial

derivative of s(x, t) with respect to x is zero

2. v(x, t) (the variable portion) will satisfy the corresponding nonhomogeneous equation with

homogeneous boundary conditions

Doing so yields two initial condition-boundary value problems that have to be solved. For

v(x, t), the variable portion of the solution, we have the nonhomogeneous partial differential

equation

∂

∂t

v(x, t) = c



∂

∂x

v(x, t)



−



∂

∂t

s(x, t)



+h(x, t)

with the corresponding homogeneous boundary conditions

v(0,t)+κ

(0,t)= 0

and

v(a, t) +κ

(a, t) = 0

and initial conditions

v(x, 0) = f(x) −s(x, 0)

and

(x, 0) = g(x) −s

(x, 0)

For s(x, t), the spatially linear portion of the solution, we have

∂

∂x

s(x, t) = 0

with nonhomogeneous boundary conditions

A(t) = κ

s(0,t)+κ

(0,t)

and

B(t) = κ

s(a, t) +κ

(a, t)

Nonhomogeneous Partial Differential Equations 513

We solved the exact same problem for the linear portion of the preceding solution s(x, t) for the

diffusion equation, and we got

s(x, t) =

(

B(t) −A(t)κ

)

a +κ

−κ

aA(t) +A(t)κ

−B(t)κ

a +κ

−κ

for

a +κ

−κ

= 0

We now focus on ﬁnding the solution to the remaining partial differential equation for v(x, t).

Writing

q(x, t) = h(x, t) −



∂

∂t

s(x, t)



the preceding partial differential equation for v(x, t) takes on the nonhomogeneous form

∂

∂t

v(x, t) = c



∂

∂x

v(x, t)



+q(x, t)

with the corresponding homogeneous boundary conditions

v(0,t)+κ

(0,t)= 0

and

v(a, t) +κ

(a, t) = 0

and initial conditions

v(x, 0) = f(x) −s(x, 0)

and

(x, 0) = g(x) −s

(x, 0)

Similar to what we did for the diffusion equation, we solve the preceding nonhomogeneous

partial differential equation for v(x, t) by the method of “eigenfunction expansion” where the

eigenfunctions are those associated with the corresponding homogeneous equation.

To solve the v(x, t) equation, we temporarily set q(x, t) = 0 and the partial differential equation

becomes

∂

∂t

v(x, t) = c



∂

∂x

v(x, t)



with homogeneous boundary conditions

v(0,t)+κ

(0,t)= 0

514 Chapter 8

and

v(a, t) +κ

(a, t) = 0

By the method of separation of variables, as done in Chapter 4, we set

v(x, t) = X(x)T(t)

The corresponding eigenvalue problem in x has the familiar form

X(x)+λX(x)= 0

with regular homogeneous boundary conditions

X(0) +κ

(0) = 0

and

X(a)+κ

(a) = 0

This is a regular Sturm-Liouville eigenvalue problem with an Euler-type operator. The eigen-

values and corresponding eigenfunctions are denoted, respectively, as

(x)

for n = 0, 1, 2, 3,....

The corresponding statement of orthonormality, with respect to the weight function w(x) = 1

over the interval I, reads—here, δ(n, m) is the familiar Kronecker delta function—



(x)X

(x)dx = δ(n, m)

The preceding boundary value problem is a regular Sturm-Liouville eigenvalue problem over

the ﬁnite interval I ={x |0 <x<a}, and the eigenfunctions form a “complete” set with

respect to any piecewise smooth function over this interval. If we assume the solution v(x, t)

and the nonhomogeneous function q(x, t) to both be piecewise smooth functions with respect

to x over this interval, then the eigenfunction expansions for v(x, t) and q(x, t), in terms of the

orthonormal eigenfunctions X

(x), read, respectively, as

v(x, t) =

∞



n=0

(t)X

(x)

and

q(x, t) =

∞



n=0

(t)X

(x)

Nonhomogeneous Partial Differential Equations 515

where the terms T

(t) and Q

(t) are the time-dependent Fourier coefﬁcients of v(x, t) and

q(x, t), respectively.

Because q(x, t) is already determined from knowledge of the functions h(x, t) and s(x, t),we

can evaluate the Fourier coefﬁcients Q

(t) by taking the inner product of the preceding with

respect to the orthonormal eigenfunctions and the weight function w(x) = 1. Using a procedure

similar to that in Section 8.2 yields

(t) =



q(x, t)X

(x) dx

We now focus on determining the time-dependent portion of the problem. The original

nonhomogeneous partial differential equation for the variable portion of the solution v(x, t)

reads

∂

∂t

v(x, t) = c



∂

∂x

v(x, t)



+q(x, t)

Substituting the eigenfunction expansions for v(x, t) and q(x, t) into this nonhomogeneous

partial differential equation, and assuming the validity of the formal procedures of

interchanging the summation and integration operations, yields the following series equation:

∞



n=0



(t)



(x) =

∞



n=0



(t)



(x)



(t)X

(x)



Recall that the spatial eigenfunctions X

(x) satisfy the eigenvalue equation

(x) +λ

(x) = 0

Making this substitution yields the series equation

∞



n=0



(t) +c

(t)



(x) =

∞



n=0

(t)X

(x)

Since the eigenfunctions are linearly independent, the only way this series equation can hold is

if the coefﬁcients of the eigenfunctions on the left are equal to the coefﬁcients of the same

eigenfunctions on the right. From this, we arrive at the time-dependent differential equation

for T

(t):

(t) +c

(t) = Q

(t)

From Section 1.4, a set of system basis vectors for the preceding equation (for λ

positive) is

T 1(t) = cos







and T 2(t) = sin







516 Chapter 8

From Section 1.8 on second-order initial-value problems, the corresponding second-order

Green’s function (with no damping in the system) is evaluated to be

G2(t, τ) =

sin



√

(t −τ)



√

The complete solution to this ordinary nonhomogeneous second-order differential equation in t

reads

(t) = C(n) cos







+D(n) sin









G2(t, τ)Q

(τ) dτ

Here, C(n) and D(n) are arbitrary unknown coefﬁcients. Similar to our analysis in Chapter 4,

examination of the time-dependent behavior of the preceding system, for zero damping,

reveals the nth-mode undamped angular frequency of the system to be given as

= c



Thus, our solution to the partial differential equation for v(x, t) is of the form of a particular

solution, and we write it as

v(x, t) =

∞



n=0

⎛

⎝

C(n) cos

(

)

+D(n) sin

(

)



sin

(

t −τ

))

(τ)

dτ

⎞

⎠

(x)

We demonstrate these concepts by solving an illustrative problem.

DEMONSTRATION: We seek the wave amplitude u(x, t) for transverse wave motion on a

taut rope over the interval I ={x |0 <x<1}. The left end of the rope is attached to a vertical

oscillatory motor, which provides a sinusoidal motion to the left end of the rope, and the right

end of the rope is held ﬁxed. There is no damping in the system, and there is no external

applied force acting [h(x, t) = 0]. The rope has an initial displacement distribution f(x) and

speed distribution g(x) given as follows. The wave speed is c = 1/2.

SOLUTION: The system partial differential equation is

∂

∂t

u(x, t) =

∂

∂x

u(x, t)

The initial displacement distribution is

u(x, 0) = f(x)

and the initial speed distribution is

(x, 0) = g(x)

Nonhomogeneous Partial Differential Equations 517

Since the left end of the rope is moved sinusoidally and the right end is held secure, the

boundary conditions are

u(0,t)= sin(t) and u(1,t)= 0

Comparing the boundary conditions with the generalized boundary conditions shown here,

u(0,t)+κ

(0,t)= A(t)

and

u(a, t) +κ

(a, t) = B(t)

we must set

A(t) = sin(t) and B(t) = 0

and

= 1,κ

= 0,κ

= 1,κ

= 0

With the given values for κ

, A(t), and B(t), the components for the linear portion of the

solution are evaluated to be

b(t) = sin(t)

and

m(t) =−sin(t)

Thus, the linear portion of the solution reads

s(x, t) =−x sin(t) +sin(t)

For the variable (particular) portion of the problem, the partial differential equation for v(x, t)

reads

∂

∂t

v(x, t) =

∂

∂x

v(x, t)

+q(x, t)

where q(x, t) is

q(x, t) = h(x, t) −



∂

∂t

s(x, t)



Because h(x, t) = 0, this evaluates to

q(x, t) =−x sin(t) +sin(t)