Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

478 Chapter 8

Here, A(t) and B(t) are the time-dependent, nonhomogeneous source terms at the boundaries

of the domain. We seek a solution to the preceding problem subject to the initial condition

u(x, 0) = f(x)

Our solution procedure is driven by our desire to ﬁnd a complete set of orthonormalized

eigenfunctions over the given domain, subject to an equivalent set of homogeneous boundary

conditions. To move in this direction, we take advantage of the linearity of the operator, and we

use the superposition principle where we assume our solution to be partitioned into two terms

u(x, t) = v(x, t) +s(x, t)

Depending on the character of the source term h(x, t) and the boundary conditions, the term

v(x, t) may exhibit the characteristics of a “variable” or “transient” solution and s(x, t) will

exhibit the characteristics of a “steady-state” or “equilibrium” solution.

We now substitute this assumed solution into the partial differential equation and get

∂

∂t

v(x, t) +

∂

∂t

s(x, t) = k



∂

∂x

v(x, t) +

∂

∂x

s(x, t)



+h(x, t)

Doing the same with the boundary conditions, we get

A(t) = κ

v(0,t)+κ

(0,t)+κ

s(0,t)+κ

(0,t)

and

B(t) = κ

v(a, t) +κ

(a, t) +κ

s(a, t) +κ

(a, t)

Similarly, substituting into the initial condition, we get

f(x) = v(x, 0) +s(x, 0)

Depending on the character of the boundary conditions, our goal now is to substitute

conditions on the partitioned solutions v(x, t) and s(x, t) so

1. s(x, t) (the steady-state portion) will be a linear function of x; thus, all second-order

partials with respect to x will be zero

2. v(x, t) (the variable portion) will satisfy the corresponding nonhomogeneous equation with

homogeneous boundary conditions

Doing this yields two initial condition-boundary value problems that can be easily resolved.

Nonhomogeneous Partial Differential Equations 479

For v(x, t), the variable portion of the solution, we obtain the nonhomogeneous partial

differential equation

∂

∂t

v(x, t) = k



∂

∂x

v(x, t)



−



∂

∂t

s(x, t)



+h(x, t)

with (the now) homogeneous boundary conditions

v(0,t)+κ

(0,t)= 0

and

v(a, t) +κ

(a, t) = 0

and initial conditions

v(x, 0) = f(x) −s(x, 0)

Similarly, for s(x, t), the spatially linear portion of the solution, we obtain the ordinary

homogeneous differential equation

∂

∂x

s(x, t) = 0

with nonhomogeneous boundary conditions

A(t) = κ

s(0,t)+κ

(0,t)

and

B(t) = κ

s(a, t) +κ

(a, t)

We now focus on ﬁnding solutions for the variable and linear portions of the problem.

Solution for the Linear Portion

We ﬁrst solve for s(x, t). From the earlier ordinary differential equation for s(x, t), the two basis

vectors with respect to the variable x are

s1(x) = 1 and s2(x) = x

Thus, the general solution to s(x, t) is the linear (with respect to x) equation

s(x, t) = m(t)x +b(t)

Note that the coefﬁcients m(t) and b(t) in the preceding linear equation are exclusively time

dependent. Substituting the preceding nonhomogeneous boundary conditions yields

b(t) +κ

m(t) = A(t)

480 Chapter 8

and

(m(t)a +b(t)) +κ

m(t) = B(t)

Solving the preceding for m(t) and b(t),weget

b(t) =

aA(t) +A(t)κ

−B(t)κ

a +κ

−κ

and

m(t) =

B(t) −A(t)κ

a +κ

−κ

Thus, the ﬁnal form for the linear (steady-state) portion of the solution s(x, t) reads

s(x, t) =

(

B(t) −A(t)κ

)

a +κ

−κ

aA(t) +A(t)κ

−B(t)κ

a +κ

−κ

for

a +κ

−κ

= 0

This is the linear or steady-state portion of the solution to the problem.

Solution for the Variable Portion

We now focus on ﬁnding the solution to the remaining partial differential equation for v(x, t).

If we write

q(x, t) = h(x, t) −



∂

∂t

s(x, t)



then the earlier partial differential equation in v(x, t) takes on the nonhomogeneous form

∂

∂t

v(x, t) = k



∂

∂x

v(x, t)



+q(x, t)

with the homogeneous boundary conditions

v(0,t)+κ

(0,t)= 0

and

v(a, t) +κ

(a, t) = 0

and initial condition

v(x, 0) = f(x) −s(x, 0)

Nonhomogeneous Partial Differential Equations 481

Note that the boundary conditions on v(x, t) are now homogeneous. The partial differential

equation continues to be nonhomogeneous because of the presence of the source term q(x, t).

We solve the preceding nonhomogeneous partial differential equation for v(x, t) by the method

of “eigenfunction expansion” where the eigenfunctions are those associated with the

corresponding homogeneous equation. The procedure goes as follows.

To solve for v(x, t), we temporarily set q(x, t) = 0. This yields the corresponding homogeneous

partial differential equation

∂

∂t

v(x, t) = k



∂

∂x

v(x, t)



with homogeneous boundary conditions

v(0,t)+κ

(0,t)= 0

and

v(a, t) +κ

(

a, t

)

= 0

By the method of separation of variables, as done in Chapter 3, we set v(x, t) to be a product

of two functions: one that is an exclusive function of x and one that is an exclusive

function of t:

v(x, t) = X(x)T(t) (8.1)

The resulting eigenvalue problem in the variable x has the form

X(x)+λX(x)= 0

with regular homogeneous boundary conditions

X(0) +κ

(0) = 0

and

X(a)+κ

(a) = 0

This is a familiar regular Sturm-Liouville eigenvalue problem where the differential equation is

of the Euler type, and the boundary conditions are homogeneous. We solve this equation for

the eigenvalues and corresponding eigenfunctions, and we denote the indexed eigenvalues and

corresponding eigenfunctions, respectively, as

(x)

for n = 0, 1, 2, 3,....

482 Chapter 8

These eigenfunctions can be orthonormalized over the interval I with respect to the weight

function w(x) = 1. The resulting statement of orthonormality reads



(x)X

(x)dx = δ(n, m)

for n, m = 0, 1, 2, 3,.... Recall, δ(n, m) is the familiar Kronecker delta function.

Since the preceding boundary value problem is a regular Sturm-Liouville problem over the

ﬁnite interval I ={x |0 <x<a}, then the eigenfunctions form a “complete” set with respect to

any piecewise smooth function over this interval. Using similar arguments from Section 2.4, if

we assume the solution v(x, t) to be a piecewise smooth function with respect to the variable x

over this interval, then the eigenfunction expansion solution of v(x, t), in terms of the

“complete” set of orthonormalized eigenfunctions X

(x), reads

v(x, t) =

∞



n=0

(t)X

(x)

Here, the terms T

(t) are the time-dependent Fourier coefﬁcients in the expansion of v(x, t).

To determine the Fourier coefﬁcients, we face having to substitute the series solution for v(x, t)

into the partial differential equation. Thus, we will be differentiating the inﬁnite series, and this

can be a tricky process. Note, however, that the preceding series is an expansion in terms of

eigenfunctions X

(x), which satisfy the same boundary conditions as v(x, t). This condition is

in our favor for making the term-by-term differentiation of the series legitimate. Without proof,

it can be simply stated that if v(x, t) and its derivatives with respect to both x and t are

continuous, and if v(x, t) satisﬁes the same spatial boundary conditions as X

(x), then term by

term differentiation of the inﬁnite series is justiﬁed.

We now deal with the nonhomogeneous term q(x, t). In a similar manner, if we assume q(x, t)

to be a piecewise smooth function with respect to the variable x over this interval, then the

eigenfunction expansion of q(x, t), in terms of the “complete” set of orthonormalized

eigenfunctions X

(x), reads

q(x, t) =

∞



n=0

(t)X

(x)

Here, the terms Q

(t) are the time-dependent Fourier coefﬁcients of q(x, t). Since q(x, t) is

already determined from knowledge of the two functions h(x, t) and s(x, t) as shown earlier,

then we can evaluate the Fourier coefﬁcents Q

(t) by taking the inner product of the preceding

with respect to the orthonormal eigenfunctions and the weight function w(x) = 1. Doing so

yields



q(x, t)X

(x)dx =

∞



n=0

(t)

⎛

⎝



(x)X

(x)dx

⎞

⎠

Nonhomogeneous Partial Differential Equations 483

Taking advantage of the orthonormality of the eigenfunctions, this reduces to



q(x, t)X

(x)dx =

∞



n=0

(t)δ(m, n)

Due to the mathematical nature of the Kronecker delta function, only one term survives the

sum, and we evaluate the coefﬁcients Q

(t) to be

(t) =



q(x, t)X

(x)dx

We now focus on determining the time-dependent portion of the problem. The original

nonhomogeneous partial differential equation for the variable portion of the solution v(x, t)

reads

∂

∂t

v(x, t) = k



∂

∂x

v(x, t)



+q(x, t)

Substituting the eigenfunction expansions for v(x, t)

v(x, t) =

∞



n=0

(t)X

(x)

and for q(x, t)

q(x, t) =

∞



n=0

(t)X

(x)

into the preceding nonhomogeneous partial differential equation, and assuming the validity of

the formal procedures of interchanging the summation and integration operations, we get

the following series equation:

∞



n=0



(t)



(x) =

∞



n=0



(t)



(x)



(t)X

(x)



Recall that the spatial eigenfunctions X

(x) satisfy the eigenvalue equation

(x) +λ

(x) = 0

Making this substitution in the preceding equation yields the series equation

∞



n=0



(t) +kλ

(t)



(x) =

∞



n=0

(t)X

(x)

484 Chapter 8

Since the eigenfunctions are linearly independent (orthogonal sets are linearly independent),

the only way this series equation can hold is if the coefﬁcients of the eigenfunctions on the left

are equal to the coefﬁcients of the same eigenfunctions on the right. From this, we arrive at the

time-dependent differential equation for T

(t):

(t) +kλ

(t) = Q

(t)

This is a ﬁrst-order nonhomogeneous differential equation. From Section 1.2, the system basis

vector for this equation is

T 1(t) = e

−kλ

and the corresponding ﬁrst-order Green’s function is

G1(t, τ) = e

−kλ

(t−τ)

Thus, from Section 1.3 on ﬁrst-order initial value problems, the solution to the nonhomo-

geneous ordinary differential equation in t reads

(t) = C(n)e

−kλ



G1(t, τ)Q

(τ)dτ

where the C(n) are arbitrary constants.

The ﬁnal solution for v(x, t) can be written as the superposition of the products of the solutions

to X

(x) and T

(t); that is,

(x, t) = X

(x)T

(t)

for n = 0, 1, 2, 3,....Thus, our solution to the partial differential equation for the variable

(transient) portion v(x, t) reads

v(x, t) =

∞



n=0

⎛

⎝

C(n)e

−kλ



G1(t, τ)Q

(τ)dτ

⎞

⎠

(x)

We demonstrate these concepts with the solution of an illustrative problem.

DEMONSTRATION: We seek the temperature distribution u(x, t) in a thin rod whose lateral

surface is insulated over the interval I ={x |0 <x<1}. The left end of the rod is up against a

temperature bath with an oscillatory temperature variation, and the right end is held at the ﬁxed

temperature of zero. There is no internal heat source (h(x, t) = 0), the initial temperature

distribution u(x, 0) = f(x) is given as follows, and the diffusivity is k = 1/4.

Nonhomogeneous Partial Differential Equations 485

SOLUTION: The system partial differential equation is

∂

∂t

u(x, t) =

∂

∂x

u(x, t)

The initial condition temperature distribution is

u(x, 0) = f(x)

where

f(x) = x(1 −x)

Since the left end of the rod is in contact with an oscillatory heat bath and the right end is held

at the ﬁxed temperature zero, the boundary conditions on the problem are

u(0,t)= sin(t) and u(1,t)= 0

In seeking the linear portion of the solution, we ﬁrst compare the boundary conditions with the

generalized nonhomogeneous boundary conditions that read

u(0,t)+κ

(0,t)= A(t)

and

u(a, t) +κ

(a, t) = B(t)

Comparing the boundary conditions with these generalized conditions, we identify the

following:

A(t) = sin(t), B(t) = 0

= 1,κ

= 0,κ

= 1,κ

= 0

With the given values for κ

, A(t), and B(t), we use the previous generalized equations for b(t)

and m(t) to solve for the components of the linear portion, and we get

b(t) = sin(t)

m(t) =−sin(t)

Thus, the linear portion of the solution reads

s(x, t) =−sin(t)x +sin(t)

For the variable portion of the problem, the partial differential equation for v(x, t) reads

∂

∂t

v(x, t) =

∂

∂x

v(x, t)

+q(x, t)

486 Chapter 8

where, from the preceding,

q(x, t) =−



∂

∂t

s(x, t)



Because h(x, t) = 0, this evaluates to

q(x, t) = x cos(t) −cos(t)

The corresponding homogeneous boundary conditions on v(x, t) are

v(0,t)= 0 and v(1,t)= 0

and the initial conditions are

v(x, 0) = f(x) −s(x, 0)

which evaluates to

v(x, 0) = x(1 −x)

To solve the v(x, t) equation, we temporarily set q(x, t) = 0, and we assume a solution of the

form

v(x, t) = X(x)T(t)

From the method of separation of variables, the corresponding spatial-dependent equation is

the Euler differential equation

X(x)+λX(x) = 0

with the corresponding homogeneous boundary conditions (type 1 at x = 0 and type 1 at x = 1)

X(0) = 0 and X(1) = 0

This eigenvalue problem was examined previously in Example 2.5.1, and the allowed

eigenvalues and corresponding orthonormal eigenfunctions are

= n

and

(x) =

√

2 sin(nπ x)

for n = 1, 2, 3,....

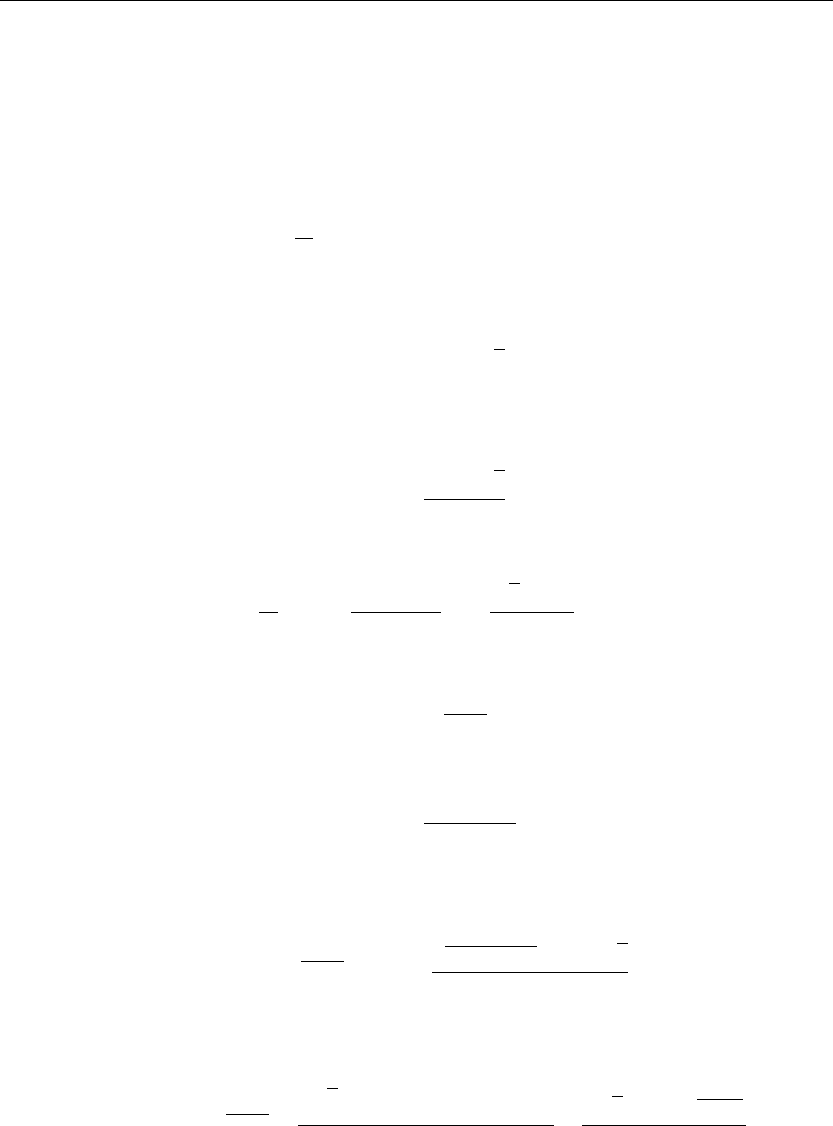
Nonhomogeneous Partial Differential Equations 487

The corresponding statement of orthonormality, with the weight function w(x) = 1, reads



2 sin(nπx) sin(mπx)dx = δ(n, m)

We now focus on the nonhomogeneous time-dependent differential equation, which reads

(t) +kλ

(t) = Q

(t)

where Q

(t) is the inner product of q(x, t) with the spatial eigenfunctions; that is,

(t) =



(cos(t)x −cos(t))

√

2 sin(nπx)dx

Evaluation of this inner product yields

(t) =−

cos(t)

√

nπ

Thus, the time-dependent differential equation reads

(t) +

(t)

=−

√

2 cos(t)

nπ

A basis vector for this differential equation, from Section 1.3, reads

T 1(t) = e

−

Evaluation of the corresponding ﬁrst-order Green’s function yields

G1(t, τ) = e

(−t+τ)

Thus, the time-dependent solution for the variable portion v(x, t) is

(t) = C(n)e

−



⎛

⎜

⎝

−

(−t+τ)

cos(τ)

√

nπ

⎞

⎟

⎠

dτ

for n = 1, 2, 3,.... Evaluating the preceding integral yields

(t) = C(n)e

−

√



cos(t) +4 sin(t)





+16



nπ

√

−

nπ



+16

