Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


458 Chapter 7
From Section 7.8, the double Fourier coefficients A(m, n) and B(m, n) are determined from the
integrals
> A(2,n):=Int(Int(f(r,theta)*R[2,n](r)*Theta[2](theta)*w(r),r=0..a),theta=0..b);
A(2,n):=
π
0
1
0
2r
3
cos
(
2θ
)
2
BesselJ
2,λ
2,n
r
BesselJ
1,λ
2,n
√
π
dr dθ (7.122)
> A(2,n):=subs(BesselJ(0,lambda[2,n]*a)=2*BesselJ(1,lambda[2,n]*a)/(lambda[2,n]*a),
value(%));
A(2,n):= −
√
π
λ
2,n
(7.123)
> B(2,n):=Int(Int((f(r,theta)*gamma/2+g(r,theta))/(omega[2,n])*R[2,n](r)*Theta[2](theta)*
w(r),r=0..a),theta=0..b);
B(2,n):=
π
0
1
0
0dr dθ (7.124)
> B(2,n):=value(%);
B(2,n):= 0 (7.125)
> T[2,n](t):=eval(subs(m=2,T[m,n](t)));
T
2,n
(t) := −
√
π cos
1
2
λ
2
2,n
t
λ
2,n
(7.126)
Generalized series terms
> u[2,n](r,theta,t):=eval(T[2,n](t)*R[2,n](r)*Theta[2](theta));
u
2,n
(r,θ,t):= −
2 cos
1
2
λ
2
2,n
t
BesselJ
2,λ
2,n
r
cos
(
2θ
)
λ
2,n
BesselJ
1,λ
2,n
(7.127)
Series solution
> u(r,theta,t):=Sum(u[2,n](r,theta,t),n=1..infinity);
u(r,θ,t):=
∞
n=1
⎛
⎜
⎝
−
2 cos
1
2
λ
2
2,n
t
BesselJ
2,λ
2,n
r
cos
(
2θ
)
λ
2,n
BesselJ
1,λ
2,n
⎞
⎟
⎠
(7.128)
Evaluation of the eigenvalues λ
2,n
from the roots of the eigenvalue equation yields
The Wave Equation in Two Spatial Dimensions 459
> subs({r=a,m=2},BesselJ(mu[m],lambda[m,n]*r))=0;
BesselJ
2,λ
2,n
= 0 (7.129)
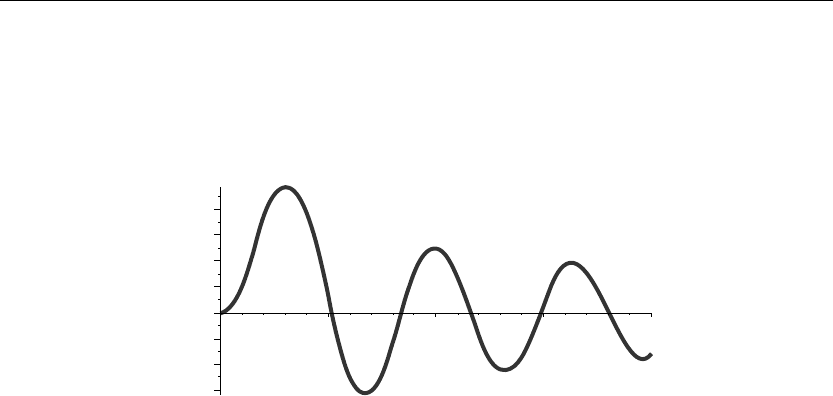
> plot(BesselJ(2,v),v=0..20,thickness=10);
0.4
0.3
0.2
20.1
20.2
20.3
0
0.1
510
v
15 20
Figure 7.11
If we set v = λa, then the eigenvalues λ
2,n
are the roots of the equation J(2,v) shown in
Figure 7.11. A few of these eigenvalues are evaluated here using the Maple fsolve command
> lambda[2,1]:=(1/a)*fsolve(BesselJ(2,v)=0,v=1..6);
λ
2,1
:= 5.135622302 (7.130)
> lambda[2,2]:=(1/a)*fsolve(BesselJ(2,v)=0,v=6..10);
λ
2,2
:= 8.417244140 (7.131)
> lambda[2,3]:=(1/a)*fsolve(BesselJ(2,v)=0,v=10..14);
λ
2,3
:= 11.61984117 (7.132)
First few terms in sum
> u(r,theta,t):=sum(u[2,n](r,theta,t),n=1..1):
ANIMATION
> u(x,y,t):=subs({r=sqrt(xˆ2+yˆ2),theta=arccos(x/sqrt(xˆ2+yˆ2))},u(r,theta,t))*
Heaviside(1-sqrt(xˆ2+yˆ2)):
> animate3d(u(x,y,t),x=-a..a,y=0..a,t=0..5,axes=framed,thickness=1);
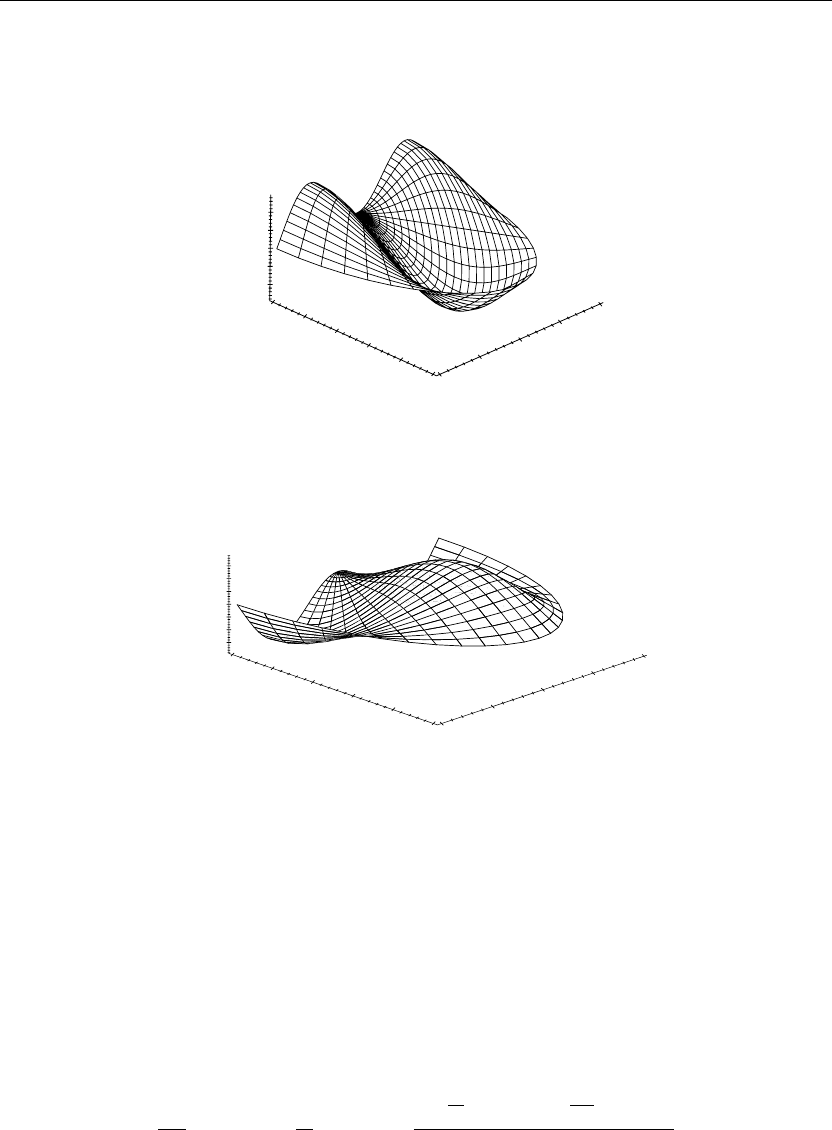
The preceding animation command illustrates the spatial-time-dependent solution for u(r,θ,t).
The animation sequence in Figures 7.12 and 7.13 shows snapshots of the animation at the times
t = 0 and t = 4.
460 Chapter 7
ANIMATION SEQUENCE
> u(r,theta,0):=subs(t=0,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,0)],r=0..a,theta=0..b,
axes=framed,thickness=1);
0.4
0.2
20.2
20.4
0
0.2
0.4
0.6
0.8
11
0.5
0
20.5
21
0
z
y
x
Figure 7.12
> u(r,theta,4):=subs(t=4,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,4)],r=0..a,theta=0..b,
axes=framed,thickness=1);
20.3
20.2
20.1
0
0.1
0.2
0.3
0
0.4
0.5
20.5
21
0
0.6
0.8
1
1
x
0.2
y
z
Figure 7.13
EXAMPLE 7.9.3: We seek the wave amplitude u(r,θ,t) for transverse waves on a thin
circularly symmetric membrane in a viscous medium over the two-dimensional domain
D ={(r, θ) |0 <r<1, 0 <θ<2π}. The damping coefficient γ is very small and the wave
speed is c = 1. The membrane is clamped at its circular edge. The initial displacement function
f(r) and the initial speed function g(r) are given as follows. Because the membrane is
circularly symmetric and the initial distributions are θ-independent, then the solution is also
θ-independent.
SOLUTION: The two-dimensional homogeneous wave equation in cylindrical coordinates for
a θ-independent system reads
∂
2
∂t
2
u(r, t) +γ
∂
∂t
u(r, t)
=
c
2
∂
∂r
u(r, t) +r
∂
2
∂r
2
u(r, t)
r

The Wave Equation in Two Spatial Dimensions 461
The boundary conditions are type 1 at r = 1, and we require a finite solution at the origin:
u(1,t)= 0 and |u(0,t)| < ∞
The initial conditions are
u(r, 0) = 1 −r
2
and u
t
(r, 0) = 0
The ordinary differential equations from the method of separation of variables are
d
2
dt
2
T
(
t
)
+γ
d
dt
T(t)
+c
2
λ
2
T(t) = 0
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
+λ
2
r
2
R(r) = 0
The boundary conditions on the r equation are
|R(0)| < ∞ and R(1) = 0
Assignment of system parameters
> restart:with(plots):a:=1:c:=1:unprotect(gamma):gamma:=1/2:
The r-dependent equation is a Bessel differential equation of the first kind of order m = 0. The
allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Example 2.6.2. The eigenvalues λ
0,n
are the roots of the eigenvalue equation
> subs(r=a,BesselJ(0,lambda[0,n]*r))=0;
BesselJ
0,λ
0,n
= 0
(7.133)
for n = 1, 2, 3,....
Orthonormal eigenfunctions
> R[0,n](r):=BesselJ(0,lambda[0,n]*r)/sqrt(Int(BesselJ(0,lambda[0,n]*r)ˆ2*r,r=0..a));
R[0,p](r):=subs(n=p,R[0,n](r)):
R
0,n
(r) :=
BesselJ
0,λ
0,n
r
1
0
BesselJ
0,λ
0,n
r
2
r dr
(7.134)
Statement of orthonormality with weight function w(r) = r
> w(r):=r:Int(R[0,n](r)*R[0,p](r)*w(r),r=0..a)=delta(n,p);
1
0
BesselJ
0,λ
0,n
r
BesselJ
0,λ
0,p
r
r
1
0
BesselJ
0,λ
0,n
r
2
r dr
1
0
BesselJ
0,λ
0,p
r
2
r dr
dr = δ(n, p) (7.135)

462 Chapter 7
Time-dependent solution
> T[0,n](t):=exp(−gamma/2*t)*(A(0,n)*cos(omega[0,n]*t)+B(0,n)*sin(omega[0,n]*t));
T
0,n
(t) := e
−
1
4
t
A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
(7.136)
Generalized series terms
> u[0,n](r,t):=T[0,n](t)*R[0,n](r);
u
0,n
(r, t) :=
e
−
1
4
t
A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
BesselJ
0,λ
0,n
r
1
0
BesselJ
0,λ
0,n
r
2
r dr
(7.137)
Eigenfunction expansion
> u(r,t):=Sum(u[0,n](r,t),n=1..infinity);
u(r, t) :=
∞
n=1
e
−
1
4
t
A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
BesselJ
0,λ
0,n
r
1
0
BesselJ
0,λ
0,n
r
2
r dr
(7.138)
> omega[0,n]:=sqrt(4*lambda[0,n]ˆ2*cˆ2−gammaˆ2)/2;
ω
0,n
:=
1
4
16λ
2
0,n
−1 (7.139)
We consider the special case where the initial condition functions u(r, θ, 0) = f(r, θ) and
u
t
(r, θ, 0) = g(r, θ) are given as
> f(r):=1−rˆ2;
f(r) := 1 −r
2
(7.140)
> g(r):=0;
g(r) := 0 (7.141)
Eigenvalues λ
0,n
are the roots of the eigenvalue equation
> subs(r=a,BesselJ(0,lambda[0,n]*r))=0;
BesselJ
0,λ
0,n
= 0 (7.142)
Evaluation of the eigenfunctions yields
> R[0,n](r):=eval(BesselJ(0,lambda[0,n]*r)/sqrt(int(BesselJ(0,lambda[0,n]*r)ˆ2*r,r=0..a)));
R
0,n
(r) :=
BesselJ
0,λ
0,n
r
√
2
√
πλ
0,n
BesselJ
(
0,λ
0,n
)
2
+
√
πλ
0,n
BesselJ
(
1,λ
0,n
)
2
√
πλ
0,n
(7.143)

The Wave Equation in Two Spatial Dimensions 463
Substitution of the eigenvalue equation in the preceding simplifies this
> R[0,n](r):=radsimp(subs(BesselJ(0,lambda[0,n]*a)=0,R[0,n](r)));
R
0,n
(r) :=
BesselJ
0,λ
0,n
r
√
2
BesselJ
1,λ
0,n
(7.144)
From Section 7.8, the double Fourier coefficients A(m, n) and B(m, n) are determined from the
integrals:
> A(0,n):=Int(f(r)*R[0,n](r)*w(r),r=0..a);
A(0,n):=
1
0
1 −r
2
BesselJ
0,λ
0,n
r
√
2r
BesselJ
1,λ
0,n
dr (7.145)
> A(0,n):=simplify(subs(BesselJ(0,lambda[0,n]*a)=0,value(%)));
A(0,n):=
4
√
2
λ
3
0,n
(7.146)
> B(0,n):=Int((f(r)*gamma/2+g(r))/omega[0,n]*R[0,n](r)*w(r),r=0..a);
B(0,n):=
1
0
4
1
4
−
1
4
r
2
BesselJ
0,λ
0,n
r
√
2 r
16λ
2
0,n
−1 BesselJ
1,λ
0,n
dr (7.147)
> B(0,n):=simplify(subs(BesselJ(0,lambda[0,n]*a)=0,value(%)));
B(0,n):=
4
√
2
λ
3
0,n
16λ
2
0,n
−1
(7.148)
> T[0,n](t):=(eval(T[0,n](t)));
T
0,n
(t) := e
−
1
4
t
⎛
⎜
⎝
4
√
2 cos
1
4
16λ
2
0,n
−1t
λ
3
0,n
+
4
√
2 sin
1
4
16λ
2
0,n
−1t
λ
3
0,n
16λ
2
0,n
−1
⎞
⎟
⎠
(7.149)

464 Chapter 7
Generalized series terms
> u[0,n](r,t):=eval(T[0,n](t)*R[0,n](r));
u
0,n
(r, t) :=
1
BesselJ(1,λ
0
,n)
⎛
⎜
⎝
e
−
1
4
t
⎛
⎜
⎝
4
√
2 cos
1
4
16λ
2
0,n
−1 t
λ
3
0,n
+
4
√
2 sin
1
4
16λ
2
0,n
−1 t
λ
3
0,n
16λ
2
0,n
−1
⎞
⎟
⎠
BesselJ(0,λ
0,n
r)
√
2
⎞
⎟
⎠
(7.150)
Series solution
> u(r,t):=Sum(u[0,n](r,t),n=1..infinity);
u(r, t) :=
∞
n=1
1
BesselJ(1,λ
0,n
)
⎛
⎜
⎝
e
−
1
4
t
⎛
⎜
⎝
4
√
2 cos
1
4
16λ
2
0,n
−1 t
λ
3
0,n
+
4
√
2 sin
1
4
16λ
2
0,n
−1 t
λ
3
0,n
16λ
2
0,n
−1
⎞
⎟
⎠
BesselJ(0,λ
0,n
r)
√
2
⎞
⎟
⎠
(7.151)
Evaluation of eigenvalues λ
0,n
from the roots of the eigenvalue equation yields
> subs(r=a,BesselJ(0,lambda[0,n]*r)=0);
BesselJ(0,λ
0,n
) = 0 (7.152)
> plot(BesselJ(0,v),v=0..20,thickness=10);
If we set v = λa, then the eigenvalues λ
0,n
are the roots of the equation J(0,v) shown in
Figure 7.14. Evaluation of some of these eigenvalues using the Maple fsolve command yields
1
0.8
0.6
20.2
20.4
0
0.2
0.4
10 15 20
v
5
Figure 7.14

The Wave Equation in Two Spatial Dimensions 465
> lambda[0,1]:=(1/a)*fsolve(BesselJ(0,v)=0,v=1..4);
λ
0,1
:= 2.404825558 (7.153)
> lambda[0,2]:=(1/a)*fsolve(BesselJ(0,v),v=4..7);
λ
0,2
:= 5.520078110 (7.154)
> lambda[0,3]:=(1/a)*fsolve(BesselJ(0,v)=0,v=7..11);
λ
0,3
:= 8.653727913 (7.155)
First few terms in sum
> u(r,t):=sum(u[0,n](r,t),n=1..3):
ANIMATION
> u(x,y,t):=subs(r=sqrt(xˆ2+yˆ2),u(r,t))*Heaviside(1−sqrt(xˆ2+yˆ2)):
> animate3d(u(x,y,t),x=−a..a,y=−a..a,t=0..3,axes=framed,thickness=1);
The preceding animation command illustrates the spatial-time-dependent solution for u(r, t).
The animation sequence in Figures 7.15 and 7.16 shows snapshots of the animation at the times
t = 0 and t = 2.
ANIMATION SEQUENCE
> u(r,0):=subs(t=0,u(r,t)):cylinderplot([r,theta,u(r,0)],r=0..a,theta=0..2*Pi,axes=framed,
thickness=1);
0
0
0.2
0.4
0.5
1
1
0.5
0
0.6
0.8
1
20.5
21
20.5
21
z
y
x
Figure 7.15
> u(r,2):=subs(t=2,u(r,t)):cylinderplot([r,theta,u(r,2)],r=0..a,theta=0..2*Pi,axes=framed,
thickness=1);

466 Chapter 7
0
0.5
11
0.5
0
0
20.5
20.02
20.015
20.01
20.005
21
20.5
21
z
y
x
Figure 7.16
Chapter Summary
Nonhomogeneous wave equation in two dimensions in rectangular coordinates
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
−γ
∂
∂t
u(x, y, t)
+h(x, y, t)
Linear wave operator in two dimensions in rectangular coordinates
L(u) =
∂
2
∂t
2
u(x, y, t) +γ
∂
∂t
u(x, y, t)
−c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
The method of separation of variables solution
u(x, y, t) = X(x)Y(y)T(t)
Eigenfunction expansion solution for rectangular coordinates
u(r,y,t)=
∞
n=0
∞
m=0
X
m
(x)Y
n
(y)e
−
γt
2
(A(m, n) cos(ω
m, n
t) +B(m, n) sin(ω
m, n
t))
Fourier coefficients from initial conditions for rectangular coordinates
A(m, n) =
b
0
a
0
f(x, y)X
m
(x)Y
n
(y)dx dy
and
B(m, n) =
b
0
a
0
f(x,y)γ
2
+g(x, y)
X
m
(x)Y
n
(y)
ω
m, n
dx dy

The Wave Equation in Two Spatial Dimensions 467
Nonhomogeneous wave equation in two dimensions in cylindrical coordinates
∂
2
∂t
2
u(r,θ,t)= c
2
⎛
⎝
∂
∂r
u(r,θ,t)+r
∂
2
∂r
2
u(r,θ,t)
r
+
∂
2
∂θ
2
u(r,θ,t)
r
2
⎞
⎠
−γ
∂
∂t
u(r,θ,t)
+h(r,θ,t)
Linear wave operator in two dimensions in cylindrical coordinates
L(u) =
∂
2
∂t
2
u(r,θ,t)+γ
∂
∂t
u(r,θ,t)
−c
2
⎛
⎝
∂
∂r
u(r,θ,t)+r
∂
2
∂r
2
u(r,θ,t)
r
+
∂
2
∂θ
2
u(r,θ,t)
r
2
⎞
⎠
The method of separation of variables solution
u(r,θ,t)= R(r) (θ) T(t)
Eigenfunction expansion solution in cylindrical coordinates
u(r,θ,t)=
∞
n=0
∞
m=0
R
m, n
(r)
m
(θ)e
−
γt
2
(A(m, n) cos(ω
m, n
t) +B(m, n) sin(ω
m, n
t))
Initial condition Fourier coefficients for cylindrical coordinates
A(m, n) =
b
0
a
0
f(r, θ)R
m, n
(r)
m
(θ) r dr dθ
and
B(m, n) =
b
0
a
0
f(r,θ)γ
2
+g(r, θ)
R
m, n
(r)
m
(θ)r
ω
m, n
dr dθ
We have examined homogeneous partial differential equations describing wave phenomena in
two spatial dimensions for both the rectangular and the cylindrical coordinate systems.
Exercises
We now consider problems for the wave equation with homogeneous boundary conditions in
two dimensions in both the rectangular and cylindrical coordinate systems. We use the method
of separation of variables and eigenfunction expansions to evaluate the solutions.
Two Dimensions, Rectangular Coordinates
We consider the transverse wave distribution in thin membranes over the two-dimensional
domain D ={(x, y) |0 <x<a,0 <y<b} with a small amount of damping. The
