Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


448 Chapter 7
The ordinary differential equations from the method of separation of variables are
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λ
2
T(t) = 0
d
2
dθ
2
(θ)+μ
2
(θ) = 0
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
+
λ
2
r
2
−μ
2
R(r) = 0
The boundary conditions on the spatial variables are
(0) = 0 and
π
2
= 0
and
|R(0)| < ∞ and R(1) = 0
Assignment of system parameters
> restart:with(plots):a:=1:b:=Pi/2:c:=1/2:unprotect(gamma):gamma:=0:
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Examples 2.5.1 and 2.6.2.
> mu[m]:=m*Pi/b;
μ
m
:= 2m (7.72)
Eigenvalues λ
m, n
are the roots of the eigenvalue equation
> BesselJ(mu[m],lambda[m,n]*a)=0;
BesselJ(2m, λ
m, n
) = 0 (7.73)
for m = 1, 2, 3,..., and n = 1, 2, 3,....
Orthonormal eigenfunctions
> Theta[m](theta):=sqrt(2/b)*sin(m*Pi/b*theta);Theta[q](theta):=subs(m=q,Theta[m](theta)):
m
(θ) :=
2 sin(2mθ)
√
π
(7.74)
> R[m,n](r):=BesselJ(mu[m],lambda[m,n]*r)/sqrt(Int(BesselJ(mu[m],lambda[m,n]*r)ˆ2*r,
r=0..a));R[m,p](r):=subs(n=p,R[m,n](r)):
R
m, n
(r) :=
BesselJ
2m, λ
m, n
r
1
0
BesselJ
2m, λ
m, n
r
2
r dr
(7.75)

The Wave Equation in Two Spatial Dimensions 449
Statements of orthonormality with their respective weight functions
> w(r):=r:Int(R[m,n](r)*R[m,p](r)*w(r),r=0..a)=delta(n,p);
1
0
BesselJ(2m, λ
m, n
r)BesselJ(2m, λ
m, p
r)r
1
0
BesselJ
2m, λ
m, n
r
2
r dr
1
0
BesselJ
2m, λ
m, p
r
2
r dr
dr = δ(n, p) (7.76)
> w(theta):=1:Int(Theta[m](theta)*Theta[q](theta)*w(theta),theta=0..b)=delta(m,q);
1
2
π
0
4 sin(2mθ) sin(2qθ)
π
dθ = δ(m, q) (7.77)
Time-dependent solution
> T[m,n](t):=exp(−gamma/2*t)*(A(m,n)*cos(omega[m,n]*t)+B(m,n)*sin(omega[m,n]*t));
T
m, n
(t) := A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
(7.78)
Generalized series terms
> u[m,n](r,theta,t):=T[m,n](t)*R[m,n](r)*Theta[m](theta);
u
m, n
(r,θ,t):=
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
BesselJ
2m, λ
m, n
r
sin
(
2mθ
)
1
0
BesselJ
2m, λ
m, n
r
2
r dr
√
π
(7.79)
Eigenfunction expansion
> u(r,theta,t):=Sum(Sum(u[m,n](r,theta,t),m=1..infinity),n=1..infinity);
u(r,θ,t):=
∞
n=1
⎛
⎜
⎜
⎜
⎜
⎝
∞
m=1
2
A(m, n) cos
ω
m,n
t
+B(m, n) sin
ω
m, n
t
BesselJ
2 m, λ
m, n
r
sin(2mθ)
1
0
BesselJ
2m, λ
m, n
r
2
r dr
√
π
⎞
⎟
⎟
⎟
⎟
⎠
(7.80)
> omega[m,n]:=sqrt(4*lambda[m,n]ˆ2*cˆ2−gammaˆ2)/2;
ω
m, n
:=
1
2
λ
2
m, n
(7.81)
We consider the special case where the initial condition functions u(r, θ, 0) = f(r, θ) and
u
t
(r, θ, 0) = g(r, θ) are given as

450 Chapter 7
> f(r,theta):=(rˆ2−rˆ4)*sin(2*theta);
f(r, θ) :=
r
2
−r
4
sin(2θ) (7.82)
> g(r,theta):=0;
g(r, θ) := 0 (7.83)
Because f(r, θ) depends on the term sin(2mθ) for the case where m = 1, then from the given
orthonormality statement for θ, only the m = 1 term survives here and we set
> Theta[1](theta):=subs(m=1,eval(Theta[m](theta)));
1
(θ) :=
2 sin(2θ)
√
π
(7.84)
> omega[1,n]:=subs(m=1,omega[m,n]);
ω
1,n
:=
1
2
λ
2
1,n
(7.85)
Eigenvalues λ
1,n
are the roots of the eigenvalue equation
> subs({m=1,r=a},BesselJ(mu[m],lambda[1,n]*r))=0;
BesselJ
2,λ
1,n
= 0 (7.86)
For m = 1, we have the Bessel identity
> subs(m=1,BesselJ(0,lambda[m,n]*a)=2*BesselJ(1,lambda[m,n]*a)/(lambda[m,n]*a)
−BesselJ(2,lambda[m,n]*a));
BesselJ
0,λ
1,n
=
2BesselJ
1,λ
1,n
λ
1,n
−BesselJ
2,λ
1,n
(7.87)
Evaluation of the eigenfunctions and the Fourier coefficients with the preceding substitutions
yields
> R[1,n](r):=eval(subs(m=1,BesselJ(mu[m],lambda[m,n]*r)/sqrt(expand(int(subs(m=1,BesselJ
(mu[m],lambda[m,n]*r))ˆ2*r,r=0..a)))));
R
1,n
(r) :=
2BesselJ
2,λ
1,n
r
2BesselJ
0,λ
1,n
2
+2BesselJ
1,λ
1,n
2
−
8BesselJ
(
1,λ
1,n
)
2
λ
2
1,n
(7.88)
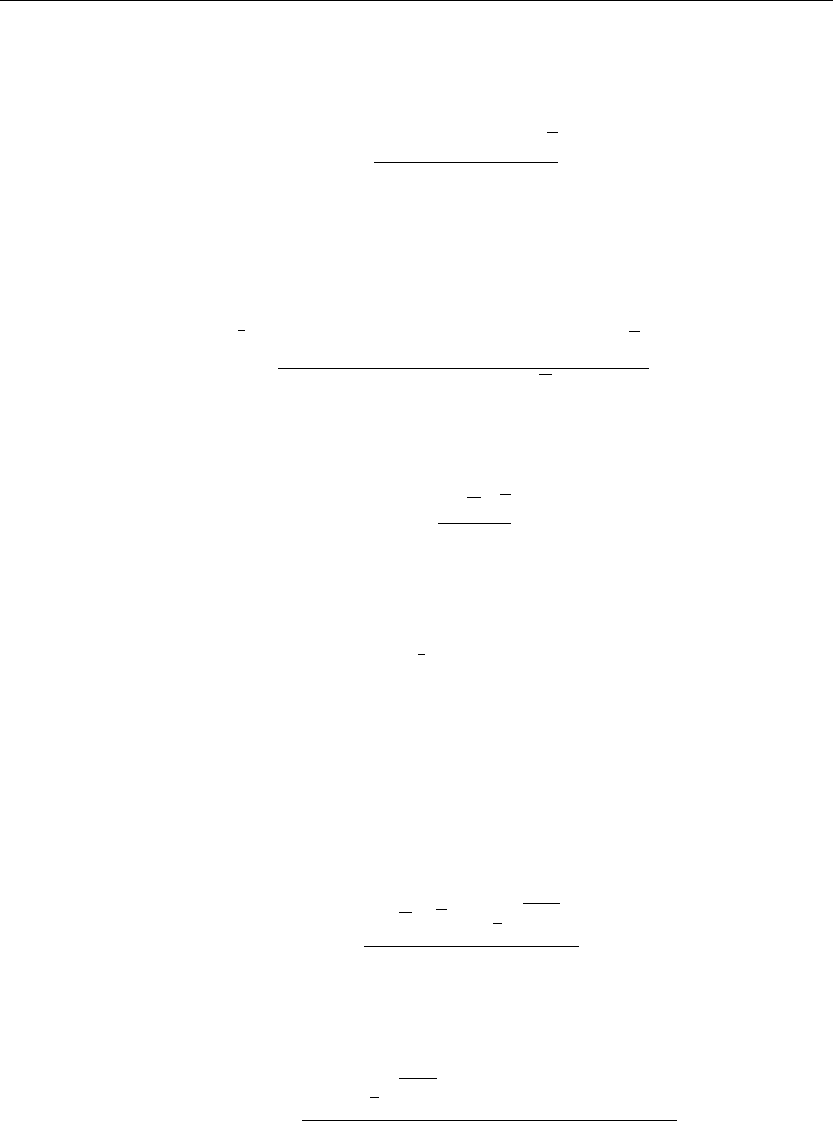
The Wave Equation in Two Spatial Dimensions 451
Substitution of the eigenvalue equation and the preceding Bessel identity simplifies this
> R[1,n](r):=radsimp(subs(BesselJ(0,lambda[1,n]*a)=2*BesselJ(1,lambda[1,n]*a)/
(lambda[1,n]*a),R[1,n](r)));
R
1,n
(r) :=
BesselJ
2,λ
1,n
r
√
2
BesselJ
1,λ
1,n
(7.89)
From Section 7.8, the double Fourier coefficients A(m, n) and B(m, n) are determined from the
integrals
> A(1,n):=Int(Int(f(r,theta)*R[1,n](r)*Theta[1](theta)*w(r),r=0..a),theta=0..b);
A(1,n):=
1
2
π
0
1
0
2
r
2
−r
4
sin
(
2θ
)
2
BesselJ
2,λ
1,n
r
√
2r
BesselJ
1,λ
1,n
√
π
dr dθ (7.90)
> A(1,n):=radsimp(subs(BesselJ(0,lambda[1,n]*a)=2*BesselJ(1,lambda[1,n]*a)/
(lambda[1,n]*a),value(%)));
A(1,n):= −
6
√
π
√
2
λ
3
1,n
(7.91)
> B(1,n):=Int(Int((f(r,theta)*gamma/2+g(r,theta))/omega[1,n]*R[1,n](r)*Theta[1](theta)*w(r),
r=0..a),theta=0..b);
B(1,n):=
1
2
π
0
1
0
0dr dθ (7.92)
> B(1,n):=radsimp(subs(BesselJ(0,lambda[1,n]*a)=2*BesselJ(1,lambda[1,n]*a)/
(lambda[1,n]*a),value(%)));
B(1,n):= 0 (7.93)
> T[1,n](t):=eval(subs(m=1,T[m,n](t)));
T
1,n
(t) := −
6
√
π
√
2 cos
1
2
λ
2
1,n
t
λ
3
1,n
(7.94)
Generalized series terms
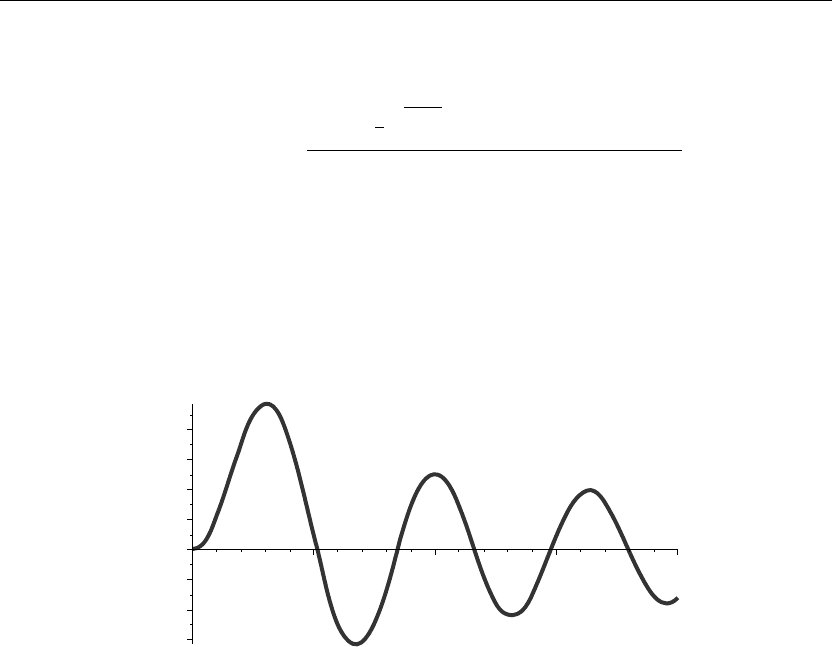
> u[1,n](r,theta,t):=eval(T[1,n](t)*R[1,n](r)*Theta[1](theta));
u
1,n
(r,θ,t):= −
24 cos
1
2
λ
2
1,n
t
BesselJ
2,λ
1,n
r
sin(2θ)
λ
3
1,n
BesselJ
1,λ
1,n
(7.95)
452 Chapter 7
Series solution
> u(r,theta,t):=Sum(u[1,n](r,theta,t),n=1..infinity);
u(r,θ,t):=
∞
n=1
⎛
⎜
⎝
−
24 cos
1
2
λ
2
1,n
t
BesselJ
2,λ
1,n
r
sin(2θ)
λ
3
1,n
BesselJ
1,λ
1,n
⎞
⎟
⎠
(7.96)
Evaluation of the eigenvalues from the roots of the eigenvalue equation yields
> subs(m=1,BesselJ(mu[m],lambda[m,n]*a)=0);
BesselJ
2,λ
1,n
= 0 (7.97)
> plot(BesselJ(2,v),v=0..20,thickness=10);
0.4
0.3
0.2
0.1
0
510
v
15 20
20.1
20.2
20.3
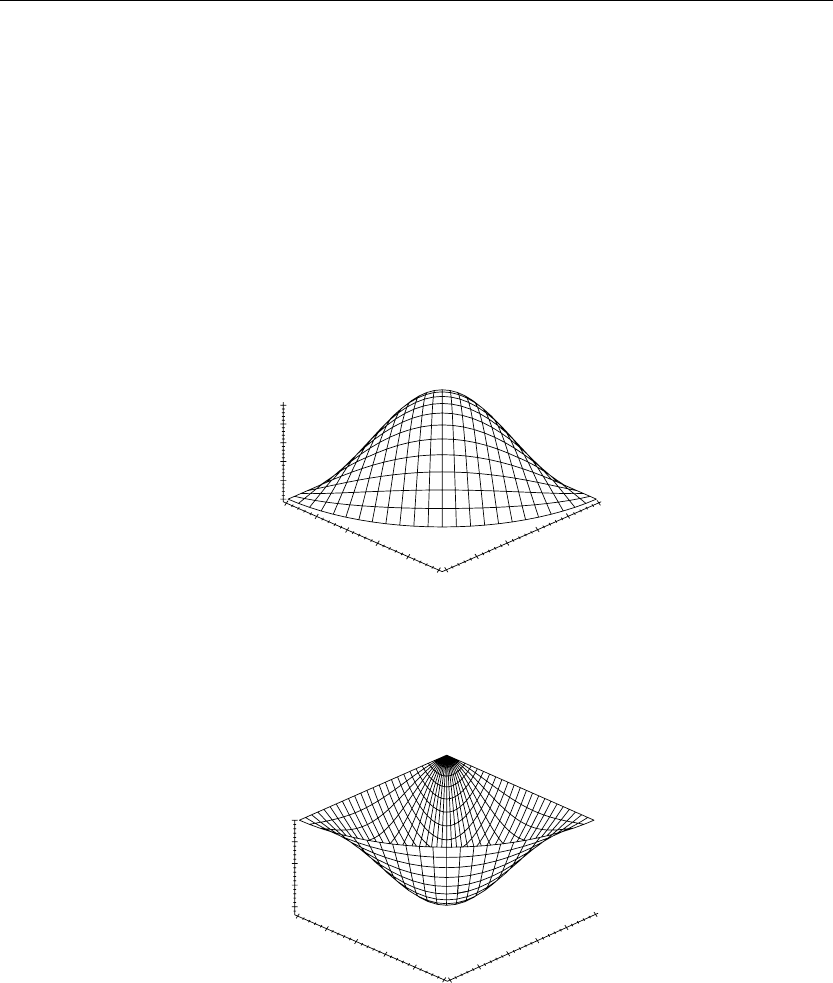
Figure 7.8
If we set v = λa, then the eigenvalues λ
1,n
are found from the intersection points of the curves
of J(2,v) with the v-axis shown in Figure 7.8. Some of these eigenvalues are calculated here
using the Maple fsolve command
> lambda[1,1]:=(1/a)*fsolve(BesselJ(2,v)=0,v=1..6);
λ
1,1
:= 5.135622302 (7.98)
> lambda[1,2]:=(1/a)*fsolve(BesselJ(2,v)=0,v=6..10);
λ
1,2
:= 8.417244140 (7.99)
> lambda[1,3]:=(1/a)*fsolve(BesselJ(2,v)=0,v=10..14);
λ
1,3
:= 13.32369194 (7.100)
First few terms in sum
> u(r,theta,t):=sum(u[1,n](r,theta,t),n=1..1):
The Wave Equation in Two Spatial Dimensions 453
ANIMATION
> u(x,y,t):=subs({r=sqrt(xˆ2+yˆ2),theta=arctan(y/x)},u(r,theta,t))*Heaviside(1−sqrt(xˆ2+yˆ2)):
> animate3d(u(x,y,t),x=0..a,y=0..a,t=0..5,axes=framed,thickness=1);
The preceding animation command illustrates the spatial-time-dependent solution for u(r,θ,t).
The animation sequence in Figures 7.9 and 7.10 shows snapshots of the animation at the times
t = 0 and t = 1.
ANIMATION SEQUENCE
> u(r,theta,0):=subs(t=0,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,0)],r=0..a,theta=0..b,
axes=framed,thickness=1);
0.15
0.1
0
0.05
0.25
0.2
0
0.2
0.4
y
z
0.6
0.8
11
0.8
0.6
0.4
x
0.2
0
Figure 7.9
> u(r,theta,1):=subs(t=1,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,1)],r=0..a,theta=0..b,
axes=framed,thickness=1);
20.15
20.1
0
20.05
20.2
0
0.2
0.4
y
z
0.6
0.8
11
0.8
0.6
0.4
x
0.2
0
Figure 7.10
EXAMPLE 7.9.2: We seek the transverse wave amplitude u(r,θ,t)for waves on a thin circular
membrane over the two-dimensional domain D ={(r, θ) |0 <r<1, 0 <θ<π}. There is no
damping in the system and the wave speed is c = 1/2. The sides θ = 0 and θ = π are free, and
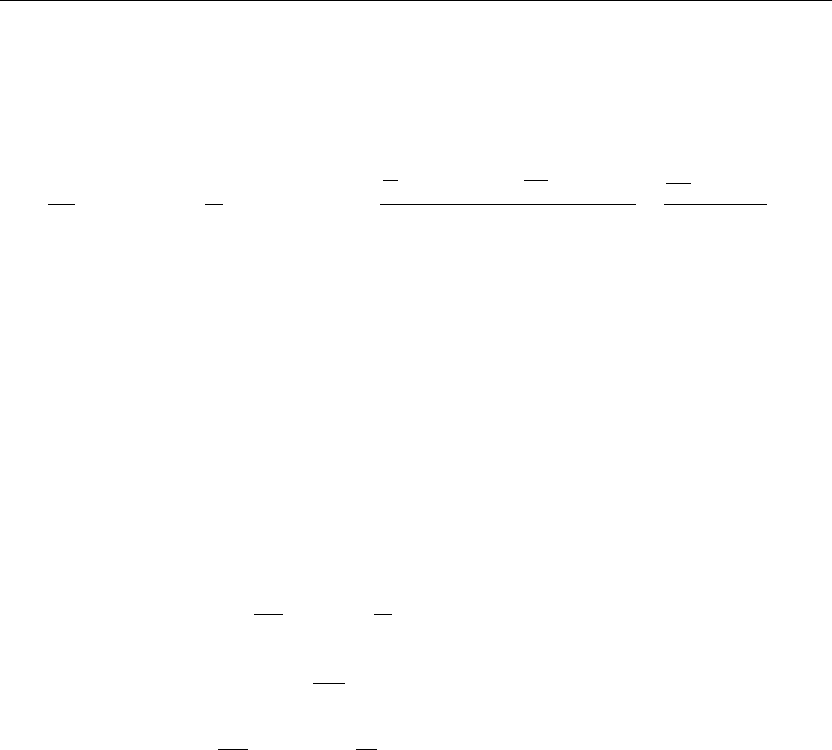
454 Chapter 7
the edge r = 1 is held fixed. The initial displacement function f(r, θ) and the initial speed
function g(r, θ) are given as follows.
SOLUTION: The two-dimensional homogeneous wave equation in cylindrical coordinates
reads
∂
2
∂t
2
u(r,θ,t)+γ
∂
∂t
u(r,θ,t)
= c
2
⎛
⎝
∂
∂r
u(r,θ,t)+r
∂
2
∂r
2
u(r,θ,t)
r
+
∂
2
∂θ
2
u(r,θ,t)
r
2
⎞
⎠
The boundary conditions are type 1 at r = 1, type 2 at θ = 0, type 2 at θ = π, and we require a
finite solution at the origin:
u(1,θ,t)= 0 and |u(0,θ,t)| < ∞
and
u
θ
(r, 0,t)= 0 and u
θ
(r,π,t)= 0
The initial conditions are
u(r, θ, 0) = r
2
cos(2θ) and u
t
(r, θ, 0) = 0
The ordinary differential equations from the method of separation of variables are
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λ
2
T(t) = 0
d
2
dθ
2
(θ)+μ
2
(θ) = 0
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
+
λ
2
r
2
−μ
2
R(r) = 0
The boundary conditions on the spatial variables are
θ
(0) = 0 and
θ
(π) = 0
and
|R(0)| < ∞ and R(1) = 0
Assignment of system parameters
> restart:with(plots):a:=1:b:=Pi:c:=1/2:unprotect(gamma):gamma:=0:
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Examples 2.5.3 and 2.6.2. For m = 1, 2, 3,..., n = 1, 2, 3,...,
> mu[m]:=m*Pi/b;
μ
m
:= m (7.101)

The Wave Equation in Two Spatial Dimensions 455
Eigenvalues λ
m, n
are the roots of the eigenvalue equation
> BesselJ(mu[m],lambda[m,n]*a)=0;
BesselJ
m, λ
m, n
= 0 (7.102)
Orthonormal eigenfunctions
> R[m,n](r):=BesselJ(mu[m],lambda[m,n]*r)/sqrt(Int(BesselJ(mu[m],lambda[m,n]*r)ˆ2*r,
r=0..a));R[m,p](r):=subs(n=p,R[m,n](r)):
R
m, n
(r) :=
BesselJ
m, λ
m, n
r
1
0
BesselJ
m, λ
m, n
r
2
r dr
(7.103)
> Theta[m](theta):=sqrt(2/b)*cos(m*Pi/b*theta);Theta[q](theta):=subs(m=q,Theta[m](theta)):
m
(θ) :=
√
2 cos(mθ)
√
π
(7.104)
For m = 0,n= 1, 2, 3,...,λ
0,n
are the roots of the equation
> BesselJ(0,lambda[0,n]*a)=0;
BesselJ
0,λ
0,n
= 0 (7.105)
Orthonormal eigenfunctions
> R[0,n](r):=BesselJ(0,lambda[0,n]*r)/sqrt(Int(BesselJ(0,lambda[0,n]*r)ˆ2*r,r=0..a));
R[0,p](r):=subs(n=p,R[0,n](r)):
R
0,n
(r) :=
BesselJ
0,λ
0,n
r
1
0
BesselJ
0,λ
0,n
r
2
r dr
(7.106)
> Theta[0](theta):=sqrt(1/b);
0
(θ) :=
1
√
π
(7.107)
Statements of orthonormality with their respective weight functions
> w(r):=r:Int(R[m,n](r)*R[m,p](r)*w(r),r=0..a)=delta(n,p);
1
0
BesselJ
m, λ
m, n
r
BesselJ
m, λ
m, p
r
r
1
0
BesselJ
m, λ
m, n
r
2
r dr
1
0
BesselJ
m, λ
m, p
r
2
r dr
dr = δ(n, p) (7.108)

456 Chapter 7
> w(theta):=1:Int(Theta[m](theta)*Theta[q](theta)*w(theta),theta=0..b)=delta(m,q);
π
0
2 cos(mθ) cos(qθ)
π
dθ = δ(m, q) (7.109)
Time-dependent solution
> T[m,n](t):=exp(−gamma/2*t)*(A(m,n)*cos(omega[m,n]*t)+B(m,n)*sin(omega[m,n]*t));
u[m,n](r,theta,t):=eval(T[m,n](t)*R[m,n](r)*Theta[m](theta)):
T
m, n
(t) := A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
(7.110)
> T[0,n](t):=exp(−gamma/2*t)*(A(0,n)*cos(omega[0,n]*t)+B(0,n)*sin(omega[0,n]*t));
u[0,n](r,theta,t):=T[0,n](t)*R[0,n](r)*Theta[0](theta):
T
0,n
(t) := A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
(7.111)
Eigenfunction expansion
> u(r,theta,t):=Sum(u[0,n](r,theta,t),n=1..infinity)+Sum(Sum(u[m,n](r,theta,t),m=1..infinity),
n=1..infinity);
u(r,θ,t):=
∞
n=1
A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
BesselJ
0,λ
0,n
r
1
0
BesselJ
0,λ
0,n
r
2
r dr
√
π
+
∞
n=1
⎛
⎜
⎜
⎜
⎜
⎝
∞
m=1
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
BesselJ
m, λ
m, n
r
√
2 cos(mθ)
1
0
BesselJ
m, λ
m, n
r
2
r dr
√
π
⎞
⎟
⎟
⎟
⎟
⎠
(7.112)
> omega[m,n]:=sqrt(4*lambda[m,n]ˆ2*cˆ2−gammaˆ2)/2;
ω
m, n
:=
1
2
λ
2
m, n
(7.113)
We consider the special case where the initial condition functions u(r, θ, 0) = f(r, θ) and
u
t
(r, θ, 0) = g(r, θ) are given as
> f(r,theta):=rˆ2*cos(2*theta);
f(r, θ) := r
2
cos(2θ) (7.114)

The Wave Equation in Two Spatial Dimensions 457
> g(r,theta):=0;
g(r, θ) := 0 (7.115)
Since f(r, θ) depends on the term cos(mθ) for the case where m = 2, then from the given
orthonormality statement for θ, only the m = 2 term survives here and we set
> Theta[2](theta):=subs(m=2,eval(Theta[m](theta)));
2
(θ) :=
√
2 cos(2θ)
√
π
(7.116)
> omega[2,n]:=subs(m=2,omega[m,n]);
ω
2,n
:=
1
2
λ
2
2,n
(7.117)
Eigenvalues λ
2,n
are the roots of the eigenvalue equation
> subs(m=2,BesselJ(mu[m],lambda[m,n]*a)=0);
BesselJ
2,λ
2,n
= 0 (7.118)
To simplify our answer, we take advantage of the Bessel identity
> BesselJ(0,lambda[2,n]*a)=2*BesselJ(1,lambda[2,n]*a)/(lambda[2,n]*a)−BesselJ
(2,lambda[2,n]*a);
BesselJ
0,λ
2,n
=
2BesselJ
1,λ
2,n
λ
2,n
−BesselJ
2,λ
2,n
(7.119)
Evaluation of the eigenfunctions and the Fourier coefficients with the preceding substitutions
yields
> R[2,n](r):=eval(subs(m=2,BesselJ(mu[m],lambda[m,n]*r)/sqrt(expand(int(subs(m=2,
BesselJ(mu[m],lambda[m,n]*r))ˆ2*r,r=0..a)))));
R
2,n
(r) :=
2BesselJ
2,λ
2,n
r
2BesselJ
0,λ
2,n
2
+2BesselJ
1,λ
2,n
2
−
8BesselJ
(
1,λ
2,n
)
2
λ
2
2,n
(7.120)
Substitution of the eigenvalue equation and the preceding Bessel identity simplifies this
> R[2,n](r):=radsimp(subs(BesselJ(0,lambda[2,n]*a)=2*BesselJ(1,lambda[2,n]*a)/
(lambda[2,n]*a),R[2,n](r)));
R
2,n
(r) :=
BesselJ
2,λ
2,n
r
√
2
BesselJ
1,λ
2,n
(7.121)
