Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

618 Chapter 9

Thus, the coefﬁcient C(ω) is found from the following Fourier transform:

> C(omega):=Int(f(y)*exp(−I*omega*y),y=−inﬁnity..inﬁnity);

C(ω) :=

∞



−∞

f(y) e

−Iωy

dy (9.92)

To solve by convolution, we can combine the two preceding integrals, as we did in Section 9.5

for the diffusion equation. Doing so, we get

> u(x,y):=Int(Int(f(zeta)/(2*Pi)*exp(−I*omega*zeta),zeta=−inﬁnity..inﬁnity)*

exp(−abs(omega)*x)*exp(I*omega*y),omega=−inﬁnity..inﬁnity);

u(x, y) :=

∞



−∞

⎛

⎝

∞



−∞

f(ζ) e

−Iωζ

dζ

⎞

⎠

−|ω|x

Iωy

dω (9.93)

Assuming the validity of the formal interchange of the order of integration yields

> u(x,y):=Int(f(zeta)*Int(exp(−abs(omega)*x)*(1/(2*Pi))*exp(I*omega*(y−zeta)),omega=

−inﬁnity..inﬁnity),zeta=−inﬁnity..inﬁnity);

u(x, y) :=

∞



−∞

f(ζ)

⎛

⎝

∞



−∞

−|ω|x

Iω(y−ζ)

dω

⎞

⎠

dζ (9.94)

If we set v = y −ζ, then we recognize the interior integral as the Fourier integral of

> assume(x>0):g(x,y−zeta):=subs(v=y−zeta,invfourier(exp(−abs(omega)*x),omega,v));

g(x∼,y−ζ) :=

x∼



x∼

+(y −ζ)



(9.95)

Thus, our solution can be written as the convolution

> u(x,y):=Int(f(zeta)*



g(x,y−zeta)



,zeta=−inﬁnity..inﬁnity);

u(x∼,y):=

∞



−∞

f(ζ)g

(

x, y −ζ

)

dζ (9.96)

We now consider the special case u(0,y)= f(y) where f(y) is given as

> f(y):=Heaviside(y+1)−Heaviside(y−1);f(zeta):=subs(y=zeta,f(y)):

f(y) := Heaviside(y +1) −Heaviside(y −1) (9.97)

Inﬁnite and Semi-inﬁnite Spatial Domains 619

Substitution of this into the previous integral yields the equivalent integral

> u(x,y):=Int(1*x/(Pi*(xˆ2+(y−zeta)ˆ2)),zeta=−1..1);

u(x∼,y):=



−1

x∼



x∼

+(y −ζ)



dζ (9.98)

This integrates to

> u(x,y):=value(%);

u(x∼,y):= −

arctan



y+1

x∼



−arctan



y−1

x∼



(9.99)

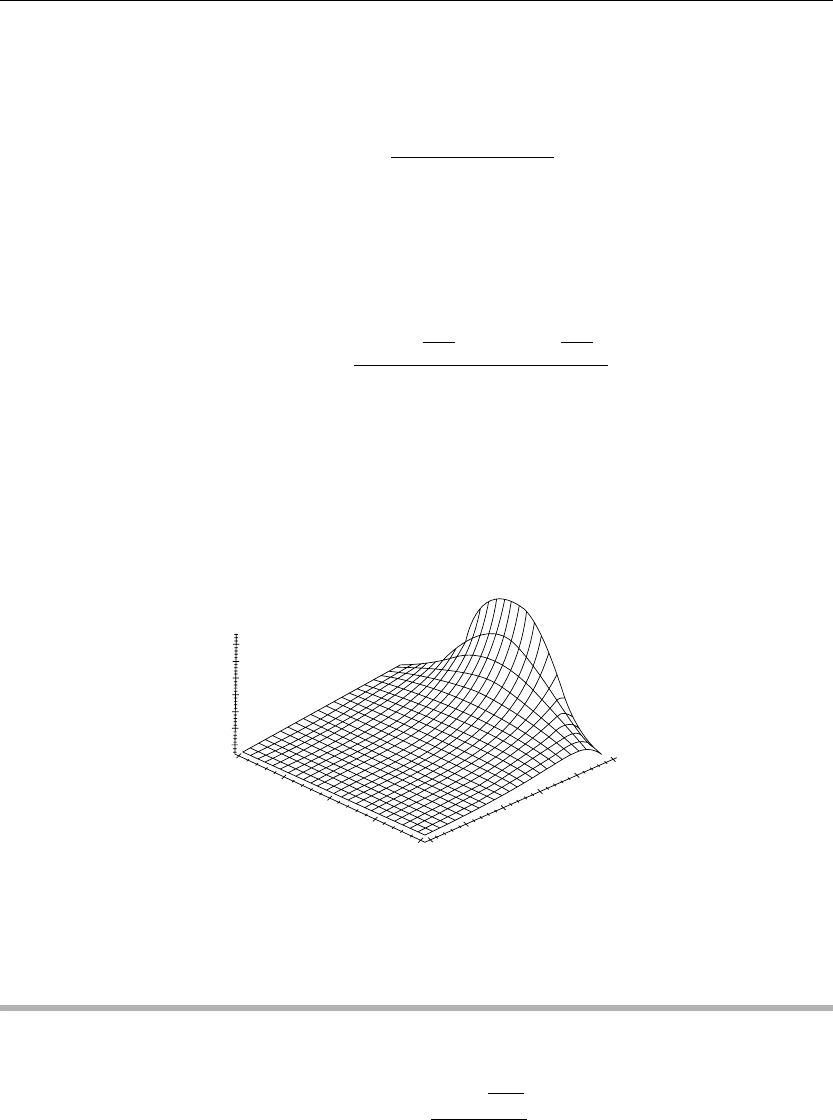
> plot3d(u(x,y),x=0..10,y=−2..2,axes=framed,thickness=1);

The three-dimensional surface shown in Figure 9.10 illustrates the electrostatic potential

distribution u(x, y) over the given region. The electrostatic equipotential lines are obtained by

clicking on the graph and choosing the “Render the plot using the polygon patch and contour

style” option and then clicking the “redraw” button in the graphics bar.

0.7

0.6

0.5

0.4

0.3

0.2

0.1

Figure 9.10

Chapter Summary

Fourier series representation of a function f(x) over a ﬁnite domain [−L,L]

f(x) =

∞



n=−∞

F(n) e

inπx

620 Chapter 9

Regular orthonormalized eigenfunctions for Euler operator over a ﬁnite domain

(x) =

√

inπx

√

for n =−3, −2, −1, 0, 1, 2, 3 ....

Statement of orthonormality for the regular eigenfunctions using the Kronecker delta function



−L

inπx

−

imπx

dx = δ(n, m)

Regular Fourier coefﬁcients

F(n) =



−L

f(x) e

−

inπ

Fourier integral representation of f(x) over an inﬁnite domain (−∞, ∞)

f(x) =

∞



−∞

F(ω) e

iωx

2π

dω

Singular orthonormalized eigenfunctions for the Euler operator over an inﬁnite domain

√

iωx

√

for −∞ <ω<∞.

Statement of orthonormality for singular eigenfunctions using the Dirac delta function

∞



−∞

iβx

−iωx

2π

dx = δ(β −ω)

Singular Fourier coefﬁcients (the Fourier integral)

F(ω) =

∞



−∞

f(x) e

−iωx

The preceding material demonstrated the parallel for the representation of functions over ﬁnite

and inﬁnite domains. For the case of ﬁnite domains, we used the Fourier series representation

Inﬁnite and Semi-inﬁnite Spatial Domains 621

in terms of the regular orthonormalized eigenfunctions where the regular Fourier coefﬁcients

are evaluated using the statement of orthonormality for regular eigenfunctions. For the case of

inﬁnite domains, we used the Fourier integral representation in terms of the singular

eigenfunctions where the singular Fourier coefﬁcients are evaluated using the equivalent

statement of orthonormality for singular eigenfunctions. Comparison of the Fourier

representation for ﬁnite domains and inﬁnite domains and the corresponding statements of

orthonormality for the regular and singular eigenfunctions shown earlier demonstrates

dramatic similarities.

Exercises

We ﬁrst consider nonhomogeneous diffusion and wave equations in a single dimension over

inﬁnite and semi-inﬁnite intervals in rectangular coordinates. For the situation of inﬁnite

intervals, we use the method of the Fourier integral, which is an extension of the eigenfunction

expansion for ﬁnite intervals. For semi-inﬁnite intervals, we use the method of Fourier sine or

cosine integrals or the method of images.

Fourier Integral Solutions of the Diffusion Equation

We consider the temperature distribution along a thin rod whose lateral surface is insulated

over either the inﬁnite interval I ={x |−∞<x<∞} or the semi-inﬁnite interval

I ={x |0 <x<∞}. We allow for an external heat source to act on the system. The

nonhomogeneous diffusion partial differential equation in rectangular coordinates in a single

dimension reads

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



+h(x, t) (9.100)

with the initial condition u(x, 0) = f(x). In Exercises 9.1 through 9.23, we seek solutions to the

preceding equation in the form of a Fourier integral with respect to x for various initial and

boundary conditions over inﬁnite or semi-inﬁnite intervals. In some instances, we use the

convolution integral or the method of images to develop the ﬁnal solution. For the following

exercises, whenever possible, generate the animated solution for u(x, t), and plot the animated

sequence for 0 <t<5.

9.1. Consider a thin cylinder over the inﬁnite interval I ={x |−∞<x<∞} containing a

ﬂuid that has an initial salt concentration density given as f(x). There is no source term

in the system, and the diffusivity is k = 1/4. Evaluate the concentration distribution

density u(x, t) in the form of a Fourier integral. Evaluate the inverse by using either the

inverse command or a convolution integral.

622 Chapter 9

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = e

−

|x|

9.2. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity is k = 1/4. Evaluate the

temperature distribution u(x, t) in the form of a Fourier integral. Evaluate the inverse by

using either the inverse command or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = x e

−

|x|

9.3. Consider a thin cylinder over the inﬁnite interval I ={x |−∞<x<∞} containing a

ﬂuid that has an initial salt concentration density given as f(x). There is no source term

in the system, and the diffusivity is k = 1/4. Evaluate the concentration distribution

density u(x, t) in the form of a Fourier integral. Evaluate the inverse by using either the

inverse command or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) =

1 +x

9.4. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity is k = 1/4. Evaluate the

temperature distribution density u(x, t) in the form of a Fourier integral. Evaluate the

inverse by using either the inverse command or a convolution integral.

Inﬁnite and Semi-inﬁnite Spatial Domains 623

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = e

−

9.5. Consider a thin cylinder over the inﬁnite interval I ={x |−∞<x<∞} containing a

ﬂuid that has an initial salt concentration density given as f(x). There is no source term

in the system, and the diffusivity is k = 1/4. Evaluate the concentration distribution

density u(x, t) in the form of a Fourier integral. Evaluate the inverse by using either the

inverse command or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = x e

−

9.6. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity is k = 1/4. Evaluate the

temperature distribution u(x, t) in the form of a Fourier integral. Evaluate the inverse by

using either the inverse command or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) =

(1 +x

)

9.7. Consider a thin cylinder over the semi-inﬁnite interval I ={x |0 <x<∞} containing a

ﬂuid that has an initial salt concentration density given as f(x). There is no source term

in the system, and the diffusivity is k = 1/4. Evaluate the concentration distribution

density u(x, t) in the form of a Fourier sine integral. Evaluate the inverse by using either

the inverse command or a convolution integral.

624 Chapter 9

Boundary conditions:

u(0,t)= 0 and

∞



|u(x, t)|dx<∞

Initial condition:

f(x) = x e

−

9.8. Consider Exercise 9.7. Develop the odd extension of f(x) and solve the problem by the

method of images.

9.9. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity is k = 1/4. Evaluate the

temperature distribution u(x, t) in the form of a Fourier sine integral. Evaluate the

inverse by using either the inverse command or a convolution integral.

Boundary conditions:

u(0,t)= 0 and

∞



|u(x, t)|dx<∞

Initial condition:

f(x) =

1 +x

9.10. Consider Exercise 9.9. Develop the odd extension of f(x) and solve the problem by the

method of images.

9.11. Consider a thin cylinder over the semi-inﬁnite interval I ={x |0 <x<∞} containing a

ﬂuid that has an initial salt concentration density given as f(x). There is no source term

in the system, and the diffusivity is k = 1/4. Evaluate the concentration distribution

density u(x, t) in the form of a Fourier sine integral. Evaluate the inverse by using either

the inverse command or a convolution integral.

Boundary conditions:

u(0,t)= 0 and

∞



|u(x, t)|dx<∞

Initial condition:

f(x) = x e

−

Inﬁnite and Semi-inﬁnite Spatial Domains 625

9.12. Consider Exercise 9.11. Develop the odd extension of f(x) and solve the problem by

the method of images.

9.13. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity is k = 1/4. Evaluate the

temperature distribution u(x, t) in the form of a Fourier cosine integral. Evaluate the

inverse by using either the inverse command or a convolution integral.

Boundary conditions:

(0,t)= 0 and

∞



|u(x, t)|dx<∞

Initial condition:

f(x) = e

−

9.14. Consider Exercise 9.13. Develop the even extension of f(x) and solve the problem by

the method of images.

9.15. Consider a thin cylinder over the semi-inﬁnite interval I ={x |0 <x<∞} containing a

ﬂuid that has an initial salt concentration density given as f(x). There is no source term

in the system, and the diffusivity is k = 1/4. Evaluate the concentration distribution

density u(x, t) in the form of a Fourier cosine integral. Evaluate the inverse by using

either the inverse command or a convolution integral.

Boundary conditions:

(0,t)= 0 and

∞



|u(x, t)|dx<∞

Initial condition:

f(x) =

1 +x

9.16. Consider Exercise 9.15. Develop the even extension of f(x) and solve the problem by

the method of images.

9.17. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity is k = 1/4. Evaluate the

temperature distribution u(x, t) in the form of a Fourier cosine integral. Evaluate the

inverse by using either the inverse command or a convolution integral.

626 Chapter 9

Boundary conditions:

(0,t)= 0 and

∞



|u(x, t)|dx<∞

Initial condition:

f(x) = e

−

9.18. Consider Exercise 9.17. Develop the even extension of f(x) and solve the problem by

the method of images.

9.19. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is a heat source term h(x, t) (dimension of degrees per second) in the system, and

the diffusivity is k = 1/4. Evaluate the temperature distribution u(x, t) in the form of a

Fourier integral. If possible, evaluate the inverse by using either the inverse command

or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = 0

Heat source:

h(x, t) = e

−

|x|

cos(t)

9.20. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is a heat source term h(x, t) (dimension of degrees per second) in the system, and

the diffusivity is k = 1/4. Evaluate the temperature distribution u(x, t) in the form of a

Fourier integral. If possible, evaluate the inverse by using either the inverse command

or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Inﬁnite and Semi-inﬁnite Spatial Domains 627

Initial condition:

f(x) = 0

Heat source:

h(x, t) = x e

−

|x|

sin(t)

9.21. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is a heat source term h(x, t) (dimension of degrees per second) in the system, and

the diffusivity is k = 1/4. Evaluate the temperature distribution u(x, t) in the form of a

Fourier integral. If possible, evaluate the inverse by using either the inverse command

or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = 0

Heat source:

h(x, t) =

cos(t)

1 +x

9.22. Consider a thin rod whose lateral surface is insulated over the inﬁnite interval

I ={x |−∞<x<∞}. The initial temperature distribution in the rod is given as f(x).

There is a heat source term h(x, t) (dimension of degrees per second) in the system, and

the diffusivity is k = 1/4. Evaluate the temperature distribution u(x, t) in the form of a

Fourier integral. If possible, evaluate the inverse by using either the inverse command

or a convolution integral.

Boundary condition:

∞



−∞

|u(x, t)|dx<∞

Initial condition:

f(x) = 0