Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


668 Chapter 10
The transform of these boundary conditions yields
κ
1
U(0,s)+κ
2
∂
∂x
U(0,s)
= Q(s)
and
U(∞,s)<∞
where the term
∂
∂x
U(0,s)is understood to be the x-dependent derivative of U(x, s) evaluated at
x = 0 and Q(s) is the Laplace transform of q(t) as shown here:
Q(s) =
∞
0
q(t) e
−st
dt
To develop the general solution to the given nonhomogeneous differential equation, we use the
method of variation of parameters as outlined in Chapter 1 whereby we must first consider
finding a set of basis vectors for the following corresponding homogeneous differential
equation:
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
= 0
A set of two basis vectors is
φ
1
(x, s) = e
−
sx
c
and
φ
2
(x, s) = e
sx
c
From the two basis vectors, we are able to generate the second-order Green’s function
G(x, v, s) =
φ
1
(v, s)φ
2
(x, s) −φ
1
(x, s)φ
2
(v, s)
W(φ
1
(v, s), φ
2
(v, s))
where the denominator term is the familiar Wronskian, which, for the basis vectors shown, is
evaluated to be
W(φ
1
(v, s), φ
2
(v, s)) =
2 s
c
Thus, from the method of varaiation of parameters, the particular solution to the
nonhomogeneous ordinary differential equation in x is
Up(x, s) =−
G(x, v, s)(sf(v) +g(v) +H(v, s))
c
2
dv

Laplace Transform Methods for Partial Diff erential Equations 669
The general solution to the x-dependent differential equation is the sum of the complementary
solution and the particular solution preceding. Combining the two solutions, we get the general
solution for the transform U(x, s):
U(x, s) = C1(s) e
−
sx
c
+C2(s) e
sx
c
−
G(x, v, s)(sf(v) +g(v) +H(v, s))
c
2
dv
The arbitrary coefficients C1(s) and C2(s) are determined from the boundary conditions for the
problem. The final solution to our problem is the inverse Laplace transform of U(x, s). We now
demonstrate these concepts by solving the illustrative problem of a string falling under its own
weight.
DEMONSTRATION: We seek the wave amplitude u(x, t) for transverse wave motion along a
taut string over the semi-infinite interval I ={x |0 <x<∞}. The left end of the string is held
secure. The string has zero initial displacement and initial speed. An external force due to
gravity (acceleration =−980 cm/sec
2
) is acting uniformly on the string, and the wave speed
constant is c = 2. There is no damping in the system.
SOLUTION: The nonhomogeneous wave partial differential equation for the string is
∂
2
∂t
2
u(x, t) = 4
∂
2
∂x
2
u(x, t)
−980
Because the string is secure at the left end and we require the solution to be finite as x
approaches infinity, the boundary conditions are
u(0,t)= 0 and u(∞,t)<∞
The string is initially at rest, and it has no initial displacement; thus, the initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = 0
The Laplace transform, with respect to t, of the partial differential equation yields the ordinary
nonhomogeneous differential equation for the transformed variable U(x, s), which reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
4
=
245
s
The corresponding transformed boundary conditions are
U(0,s)= 0 and U(∞,s)<∞
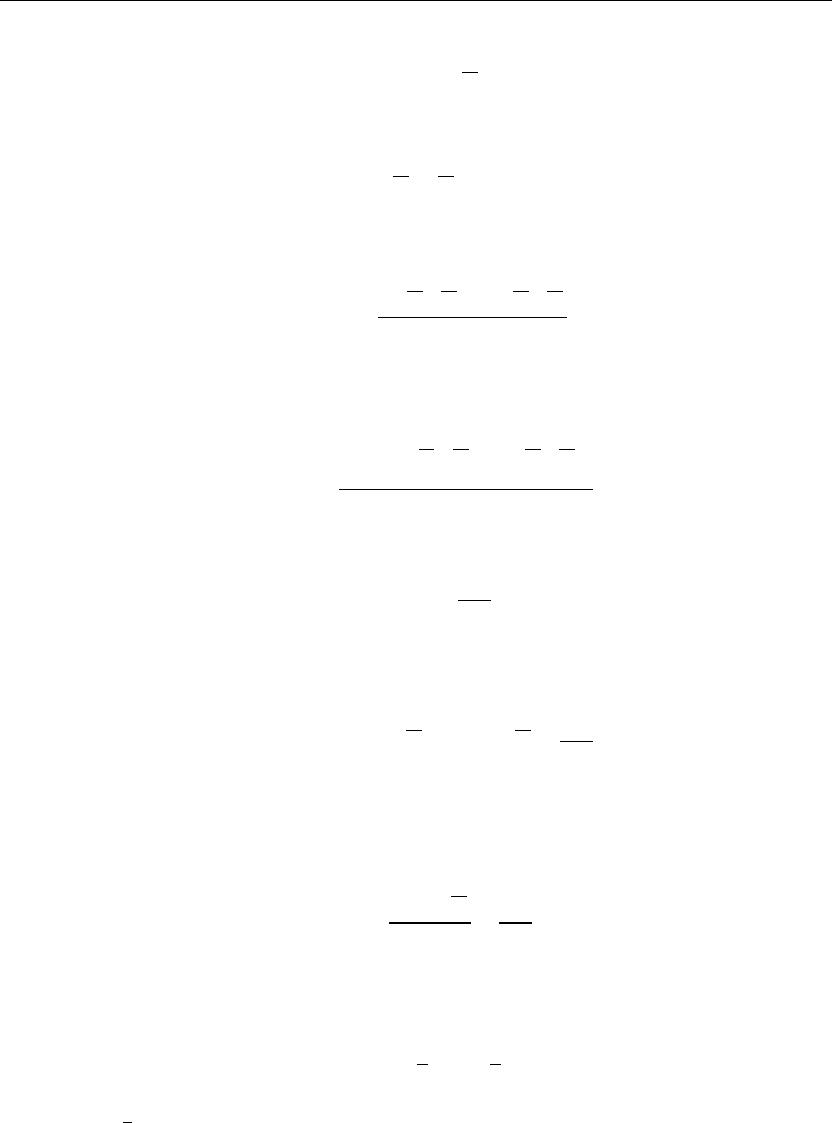
From Section 1.5, a set of basis vectors for the x-dependent differential equation is
φ
1
(x, s) = e
−
sx
2
670 Chapter 10
and
φ
2
(x, s) = e
sx
2
The Wronskian for this basis is
W
e
−
sv
2
, e
sv
2
= s
From Section 1.7, the corresponding second-order Green’s function is
G(x, v, s) =
e
−
sv
2
e
sx
2
− e
−
sx
2
e
sv
2
s
The particular solution to the nonhomogeneous differential equation, for the transformed
variable U(x, s), is given as the Green’s function integral
Up(x, s) =
245
e
−
sv
2
e
sx
2
− e
−
sx
2
e
sv
2
s
2
dv
which is evaluated to be
Up(x, s) =−
980
s
3
Thus, the general solution to the ordinary differential equation for the transformed solution
U(x, s) is
U(x, s) = C1(s) e
−
sx
2
+C2(s) e
sx
2
−
980
s
3
(10.85)
Here, C1(s) and C2(s) are arbitrary constants that are determined from the boundary
conditions. Substituting the boundary condition at x = 0 and as x approaches infinity, for
Re{s} > 0, we get the transformed solution
U(x, s) =
980 e
−
sx
2
s
3
−
980
s
3
Evaluation of the inverse Laplace transform yields the spatial- and time-dependent solution
u(x, t) for the falling string:
u(x, t) = 490 H
t −
x
2
t −
x
2
2
−490 t
2
where H
t −
x
2
denotes the translated Heaviside function. The details for the development of
this solution and the graphics are given later in one of the Maple worksheet examples.

Laplace Transform Methods for Partial Diff erential Equations 671
10.7 Example Laplace Transform Problems for the
Wave Equation
We now look at some specific applications of the Laplace transform in evaluating solutions to
the wave equation over semi-infinite domains with respect to the spatial variable x. We focus
on those types of problems that have nonhomogeneous boundary conditions—problems that
cannot ordinarily be solved using Fourier transform methods as covered in Chapter 9.
EXAMPLE 10.7.1: (The vibrating string) We seek the wave amplitude u(x, t) for transverse
wave motion along a taut string over the semi-infinite interval I ={x |0 <x<∞}. The left
end of the string is constrained to move in accordance with the sinusoidal function q(t) given
following. The string has an initial displacement distribution f(x) and an initial speed
distribution g(x). There is no external source function, and there is no damping in the system.
The wave speed is c = 2.
SOLUTION: The wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
The boundary conditions are
u(0,t)= sin(t) and u(∞,t)<∞
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = 0
The Laplace transformed equation reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
=−
sf ( x )
c
2
−
g(x)
c
2
Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary
conditions are
U(0,s)= Q(s) and U(∞,s)<∞
Assignment of system parameters
> restart:with(plots):with(inttrans):c:=2:q(t):=sin(t):f(x):=0:g(x):=0:
Transformed equation in x reads
> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2;
∂
2
∂x
2
U(x, s) −
1
4
s
2
U(x, s) = 0 (10.86)

672 Chapter 10
Transformed boundary conditions
> Q(s):=Int(q(t)*exp(−s*t),t=0..infinity);
Q(s) :=
∞
0
sin(t) e
−st
dt (10.87)
> Q(s):=laplace(q(t),t,s);
Q(s) :=
1
s
2
+1
(10.88)
General solution for U(x, s)
> assume(x>0):U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x);
U(x∼,s):= C1(s) e
−
1
2
sx∼
+C2(s) e
1
2
sx∼
(10.89)
Substituting the boundary conditions at x = 0 and as x approaches infinity, for Re{s} > 0,
we get
> C2(s):=0;
C2(s) := 0 (10.90)
> eq:=Q(s)=eval(subs(x=0,U(x,s)));
eq :=
1
s
2
+1
= C1(s) (10.91)
> C1(s):=solve(eq, C1(s));
C1(s) :=
1
s
2
+1
(10.92)
Transformed solution
> U(x,s):=eval(U(x,s));
U(x∼,s):=
e
−
1
2
sx∼
s
2
+1
(10.93)
Solution is the inverse Laplace of U(x, s)
> u(x,t):=invlaplace(U(x,s),s,t);
u(x∼,t):= Heaviside
t −
1
2
x∼
sin
t −
1
2
x∼
(10.94)
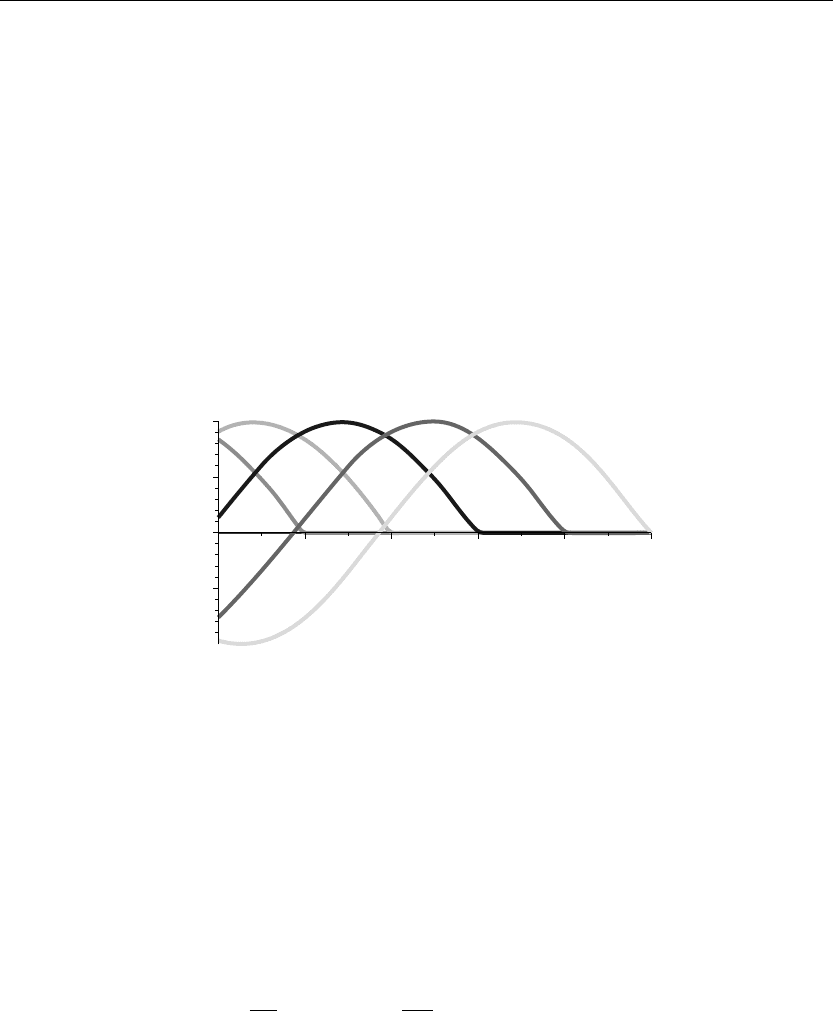
Laplace Transform Methods for Partial Diff erential Equations 673
ANIMATION
> animate(u(x,t),x=0..10,t=0..10,thickness=3);
The preceding animation command shows the spatial-time wave amplitude distribution u(x, t)
on the string. The animation sequence here and in Figure 10.7 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..10,thickness=10);
x~
1.0
0.5
0
246810
2
0.5
Figure 10.7
EXAMPLE 10.7.2: (String falling under its own weight) We seek the wave amplitude
u(x, t) for transverse wave motion along a taut string over the semi-infinite interval
I ={x |0 <x<∞}. The left end of the string is held fixed. The string has the initial
displacement distribution f(x) = 0 and the initial speed distribution g(x) = 0. An external
force due to gravity (acceleration =−980 cm/sec
2
) is acting uniformly on the string, and we
assume no damping in the system. The wave speed is c = 2.
SOLUTION: The nonhomogeneous wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
+h(x, t)
The boundary conditions are
u(0,t)= 0 and u(∞,t)<∞
674 Chapter 10
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = 0
The Laplace transformed equation reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
=−
sf ( x )
c
2
−
g(x)
c
2
−
H(x, s)
c
2
Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary
conditions are
U(0,s)= Q(s) and U(∞,s)<∞
Assignment of system parameters
> restart:with(plots):with(inttrans):c:=2:q(t):=0:f(x):=0:f(v):=subs(x=v,f(x)):g(x):=0:
g(v):=subs(x=v,g(x)):h(x,t):=−980:
Transformed equation in x reads
> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2−H(x,s)/cˆ2;
∂
2
∂x
2
U(x, s) −
1
4
s
2
U(x, s) =−
1
4
H(x, s) (10.95)
Transformed boundary conditions
> Q(s):=Int(q(t)*exp(−s*t),t=0..infinity);
Q(s) :=
∞
0
0dt (10.96)
> Q(s):=value(%);
Q(s) := 0 (10.97)
Transformed source term
> H(x,s):=Int(h(x,t)*exp(−s*t),t=0..infinity);
H(x, s) :=
∞
0
(−980 e
−st
) dt (10.98)
> H(x,s):=laplace(h(x,t),t,s);H(v,s):=subs(x=v,H(x,s)):
H(x, s) := −
980
s
(10.99)

Laplace Transform Methods for Partial Diff erential Equations 675
Basis vectors
> assume(x>0):phi[1](x,s):=exp(−s/c*x);phi[1](v,s):=subs(x=v,phi[1](x,s)):
phi[2](x,s):=exp(s/c*x);phi[2](v,s):=subs(x=v,phi[2](x,s)):
φ
1
(x∼,s):=e
−
1
2
sx∼
φ
2
(x∼,s):=e
1
2
sx∼
(10.100)
Evaluation of the Wronskian
> W(phi[1](v,s),phi[2](v,s)):=simplify(phi[1](v,s)*diff(phi[2](v,s),v)−phi[2](v,s)*
diff(phi[1](v,s),v));
W
e
−
1
2
sv
, e
1
2
sv
:= s (10.101)
Evaluation of the Green’s function
> G(x,v,s):=(phi[1](v,s)*phi[2](x,s)−phi[1](x,s)*phi[2](v,s))/W(phi[1](v,s),phi[2](v,s));
G(x∼,v,s):=
e
−
1
2
sv
e
1
2
sx∼
− e
−
1
2
sx∼
e
1
2
sv
s
(10.102)
Particular solution
> Up(x,s):=−Int(G(x,v,s)*(s*f(v)+g(v)+H(v,s))/cˆ2,v);
Up(x ∼,s):= −
⎛
⎜
⎜
⎝
⎛
⎜
⎜
⎝
−
245
e
−
1
2
sv
e
1
2
sx∼
− e
−
1
2
sx∼
e
1
2
sv
s
2
⎞
⎟
⎟
⎠
dv
⎞
⎟
⎟
⎠
(10.103)
> Up(x,s):=simplify(subs(v=x,value(%)));
Up(x ∼,s):= −
980
s
3
(10.104)
General solution
> U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x)+Up(x,s);
U(x∼,s):= C1(s) e
−
1
2
sx∼
+C2(s) e
1
2
sx∼
−
980
s
3
(10.105)

676 Chapter 10
Substituting the boundary conditions at x = 0 and as x approaches infinity, for Re{s} > 0,
we get
> C2(s):=0;
C2(s) := 0 (10.106)
> eq:=Q(s)=eval(subs(x=0,U(x,s)));
eq := 0 = C1(s) −
980
s
3
(10.107)
> C1(s):=solve(eq,C1(s));
C1(s) :=
980
s
3
(10.108)
Transformed solution for U(x, s)
> U(x,s):=eval(U(x,s));
U(x∼,s):=
980 e
−
1
2
sx∼
s
3
−
980
s
3
(10.109)
Solution is the inverse Laplace of U(x, s)
> u(x,t):=invlaplace(U(x,s),s,t);
u(x∼,t):= −490 t
2
+
245
2
Heaviside
t −
1
2
x∼
(2 t −x∼)
2
(10.110)
ANIMATION
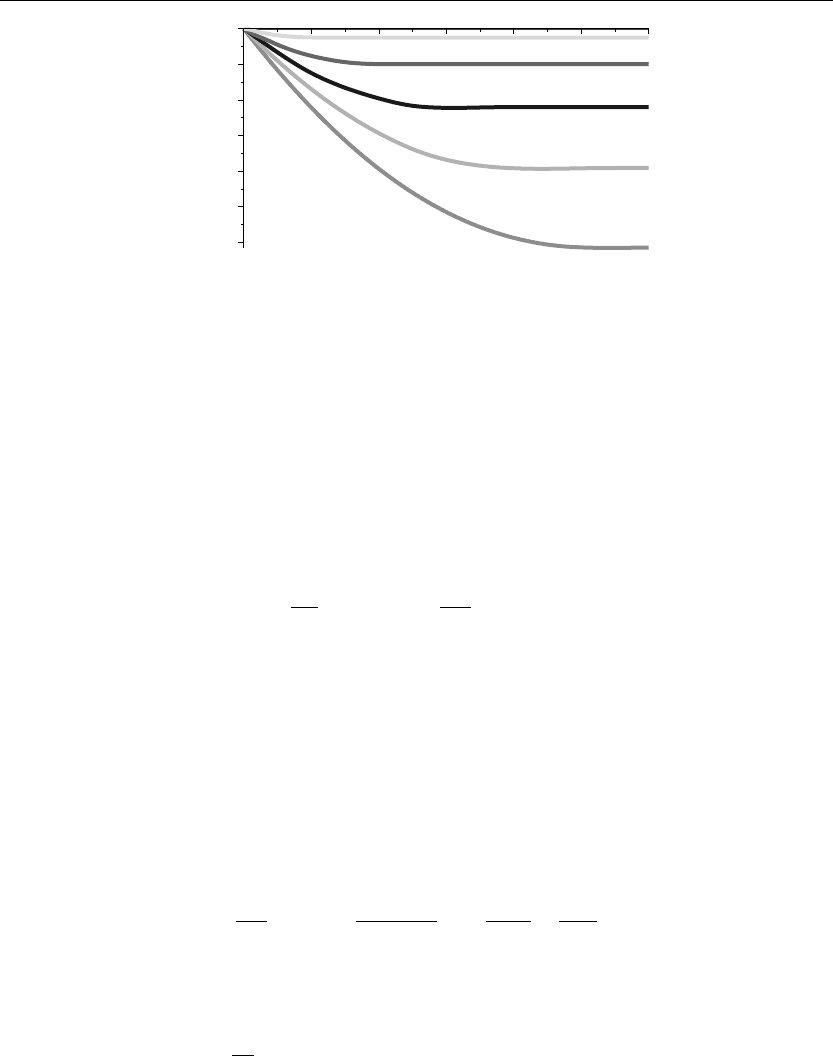
> animate(u(x,t),x=0..12,t=0..5,thickness=3);
The preceding animation command shows the spatial-time wave amplitude distribution u(x, t)
on the string. The animation sequence here and in Figure 10.8 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..12,thickness=10);
Laplace Transform Methods for Partial Diff erential Equations 677
0
24681012
2
2000
2
4000
2
6000
2
8000
2
10000
2
12000
x~
Figure 10.8
EXAMPLE 10.7.3: (Longitudinal vibrations in a bar) We seek the wave amplitude for
longitudinal wave motion in a bar over the semi-infinite interval I ={x |0 <x<∞}. The left
end of the bar is experiencing an applied stress force q(t) (the Young’s modulus E = 1). Each
cross section of the bar has the initial displacement distribution f(x) = 0 and the initial speed
distribution g(x) = 0. There are no external forces acting upon the bar, and there is no
damping. The wave speed is c = 2.
SOLUTION: The wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
The boundary conditions are
u
x
(0,t)=−cos(t) and u(∞,t)<∞
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = 0
The Laplace transformed equation reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
=−
sf ( x )
c
2
−
g(x)
c
2
Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary
conditions are
∂
∂x
U(0,s)=−Q(s) and U(∞,s)<∞
Assignment of system parameters
> restart:with(plots):with(inttrans):c:=2:q(t):=cos(t):f(x):=0:g(x):=0:
