Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


678 Chapter 10
Transformed equation in x reads
> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2;
∂
2
∂x
2
U(x, s) −
1
4
s
2
U(x, s) = 0 (10.111)
Transformed boundary conditions
> Q(s):=Int(q(t)*exp(−s*t),t=0..infinity);
Q(s) :=
∞
0
cos(t) e
−st
dt (10.112)
> Q(s):=laplace(q(t),t,s);
Q(s) :=
s
s
2
+1
(10.113)
General solution for U(x, s)
> assume(x>0):U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x);
U(x∼,s):= C1(s) e
−
1
2
sx∼
+C2(s) e
1
2
sx∼
(10.114)
Substituting the boundary conditions at x = 0 and as x approaches infinity, for Re{s} > 0, we get
> C2(s):=0;
C2(s) := 0 (10.115)
> eq:=Q(s)=−eval(subs(x=0,diff(U(x,s),x)));
eq :=
s
s
2
+1
=
1
2
C1(s)s (10.116)
> C1(s):=solve(eq,C1(s));
C1(s) :=
2
s
2
+1
(10.117)
Transformed solution
> U(x,s):=eval(U(x,s));
U(x∼,s):=
2e
−
1
2
sx∼
s
2
+1
(10.118)
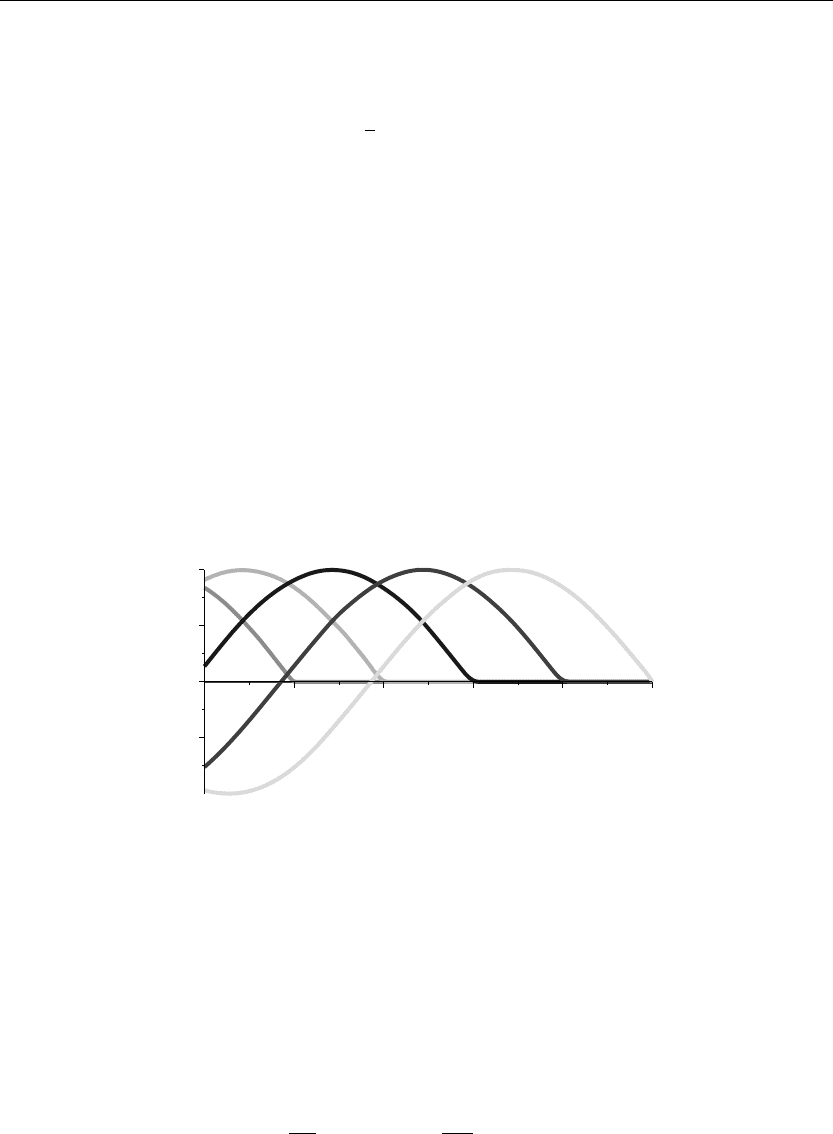
Laplace Transform Methods for Partial Diff erential Equations 679
Solution is the inverse Laplace of U(x, s)
> u(x,t):=simplify(invlaplace(U(x,s),s,t));
u(x∼,t):= −2 sin
t −
1
2
x∼
(−1 + Heaviside(x∼−2 t)) (10.119)
ANIMATION
> animate(u(x,t),x=0..10,t=0..10,thickness=3);
The preceding animation command shows the spatial-time wave amplitude distribution u(x, t)
in the bar. The animation sequence here and in Figure 10.9 shows snapshots of the animation at
times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)}x=0..10,thickness=10);
x~
2
1
0
246810
2
1
Figure 10.9
EXAMPLE 10.7.4: (Initially displaced string) We seek the wave amplitude u(x, t) for
transverse wave motion along a taut string over the semi-infinite interval I ={x |0 <x<∞}.
The left end of the string is held fixed. The string has the initial displacement distribution
u(x, 0) = f(x) given following, and the initial speed distribution g(x) = 0. There are no
external forces acting upon the string, and there is no damping in the system. The wave speed
is c = 1.
SOLUTION: The wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)

680 Chapter 10
The boundary conditions are
u(0,t)= 0 and u(∞,t)<∞
The initial conditions are
u(x, 0) = x e
−x
and u
t
(x, 0) = 0
The Laplace transformed equation reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
=−
sf ( x )
c
2
−
g(x)
c
2
Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary
conditions are
U(0,s)= Q(s) and U(∞,s)<∞
Assignment of system parameters
> restart:with(plots):with(inttrans):c:=1:q(t):=0:f(x):=x*exp(−x):f(v):=subs(x=v,f(x)):g(x):=0:
g(v):=subs(x=v,g(x)):
Transformed equation in x reads
> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2;
∂
2
∂x
2
U(x, s) −s
2
U(x, s) =−sx e
−x
(10.120)
Transformed boundary conditions
> Q(s):=Int(q(t)*exp(−s*t),t=0..infinity);
Q(s) :=
∞
0
0dt (10.121)
> Q(s):=value(%);
Q(s) := 0 (10.122)
Basis vectors
> assume(x>0):phi[1](x,s):=exp(−s/c*x);phi[1](v,s):=subs(x=v,phi[1](x,s)):phi[2](x,s)
:=exp(s/c*x);phi[2](v,s):=subs(x=v,phi[2](x,s)):
φ
1
(x∼,s):=e
−sx∼
φ
2
(x∼,s):=e
sx∼
(10.123)

Laplace Transform Methods for Partial Diff erential Equations 681
Evaluation of the Wronskian
> W(phi[1](v,s),phi[2](v,s)):=simplify(phi[1](v,s)*diff(phi[2](v,s),v)−phi[2](v,s)*
diff(phi[1](v,s),v));
W( e
−sv
, e
sv
) := 2s (10.124)
Evaluation of the Green’s function
> G(x,v,s):=(phi[1](v,s)*phi[2](x,s)−phi[1](x,s)*phi[2](v,s))/W(phi[1](v,s),phi[2](v,s));
G(x∼,v,s):=
1
2
e
−sv
e
sx∼
− e
−sx∼
e
sv
s
(10.125)
Particular solution
> Up(x,s):=−Int(G(x,v,s)*(s*f(v)+g(v))/cˆ2,v);
Up(x ∼,s):= −
1
2
( e
−sv
e
sx∼
− e
−sx∼
e
sv
)v e
−v
dv
(10.126)
> Up(x,s):=simplify(subs(v=x,value(%)));
Up(x ∼,s):=
e
−x∼
s(−x∼−2 +x∼ s
2
)
(1 +s)
2
(−1 +s)
2
(10.127)
General solution
> U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x)+Up(x,s);
U(x∼,s):= C1(s) e
−sx∼
+C2(s) e
sx∼
+
e
−x∼
s(−x∼−2 +x∼s
2
)
(1 +s)
2
(−1 +s)
2
(10.128)
Substituting the boundary conditions at x = 0 and as x approaches infinity, for Re{s} > 0, we get
> C2(s):=0;
C2(s) := 0 (10.129)
> eq:=Q(s)=eval(subs(x=0,U(x,s)));
eq := 0 = C1(s) −
2s
(1 +s)
2
(−1 +s)
2
(10.130)
> C1(s):=solve(eq,C1(s));
C1(s) :=
2s
1 −2s
2
+s
4
(10.131)
682 Chapter 10
Transformed solution for U(x, s)
> U(x,s):=eval(U(x,s));
U(x∼,s):=
2se
−sx∼
1 −2s
2
+s
4
+
e
−x∼
s(−x∼−2 +x∼s
2
)
(1 +s)
2
(−1 +s)
2
(10.132)
Solution is the inverse Laplace of U(x, s)
> u(x,t):=invlaplace(U(x,s),s,t);
u(x∼,t):= Heaviside (t −x∼)(t −x∼) sinh(t −x∼) + e
−x∼
(x∼ cosh(t) −t sinh(t))
(10.133)
ANIMATION
> animate(u(x,t),x=0..12,t=0..5,thickness=3);
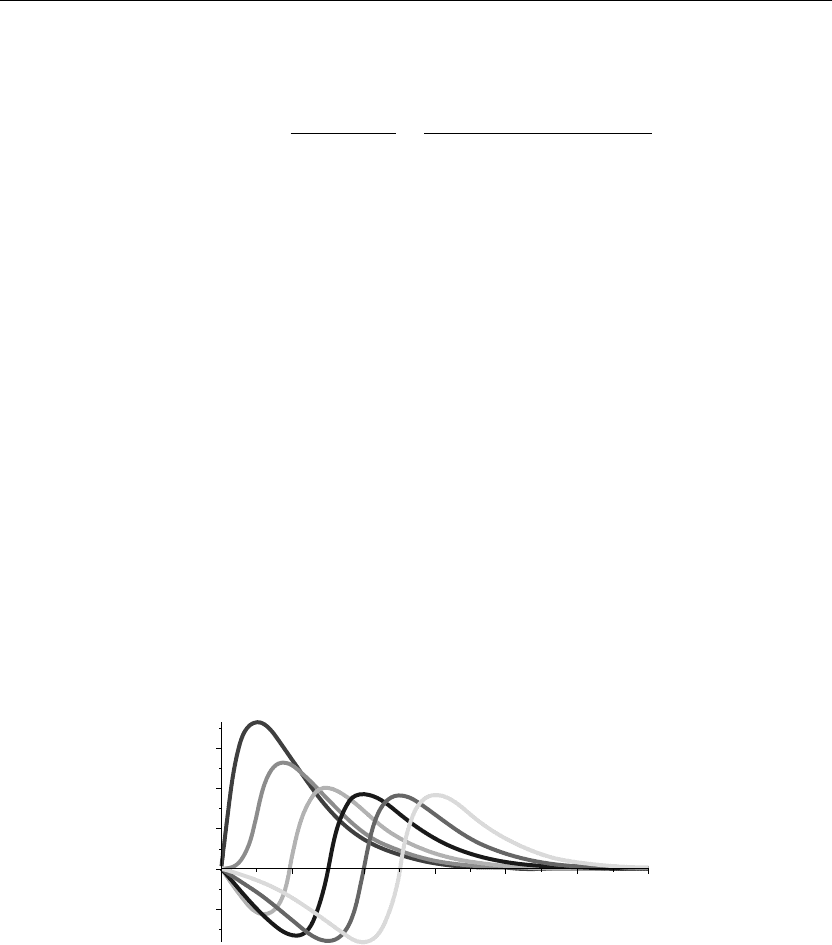
The preceding animation command shows the spatial-time amplitude distribution u(x, t) on the
string. The animation sequence here and in Figure 10.10 shows snapshots of the animation at
times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5),},x=0..12,thickness=10);
0.3
0.2
0.1
0
24681012
2
0.1
x~
Figure 10.10
EXAMPLE 10.7.5: (String with initial speed) We seek the wave amplitude u(x, t) for
transverse wave motion along a taut string over the semi-infinite interval I ={x |0 <x<∞}.
The left end of the string is held fixed. The string has an initial displacement distribution
f(x) = 0 and an initial speed distribution u
t
(x, 0) = g(x) given following. There are no
external forces acting upon the string, and there is no damping. The wave speed is c = 2.

Laplace Transform Methods for Partial Diff erential Equations 683
SOLUTION: The wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
The boundary conditions are
u(0,t)= 0 and u(∞,t)<∞
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = sin(t)
The Laplace transformed equation reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
=−
sf ( x )
c
2
−
g(x)
c
2
Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary
conditions are
U(0,s)= Q(s) and U(∞,s)<∞
Assignment of system parameters
> restart:with(plots):with(inttrans):c:=2:q(t):=0:f(x):=0:f(v):=subs(x=v,f(x)):g(x):=sin(x):
g(v):=subs(x=v,g(x)):
Transformed equation in x reads
> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2;
∂
2
∂x
2
U(x, s) −
1
4
s
2
U(x, s) =−
1
4
sin(x) (10.134)
Transformed boundary conditions
> Q(s):=Int(q(t)*exp(−s*t),t=0..infinity);
Q(s) :=
∞
0
0dt (10.135)
> Q(s):=value(%);
Q(s) := 0 (10.136)

684 Chapter 10
Basis vectors
> assume(x>0):phi[1](x,s):=exp(−s/c*x);phi[1](v,s):=subs(x=v,phi[1](x,s)):
phi[2](x,s):=exp(s/c*x);phi[2](v,s):=subs(x=v,phi[2](x,s)):
φ
1
(x∼,s):=e
−
1
2
sx∼
φ
2
(x∼,s):=e
1
2
sx∼
(10.137)
Evaluation of the Wronskian
> W(phi[1](v,s),phi[2](v,s)):=simplify(phi[1](v,s)*diff(phi[2](v,s),v)
−phi[2](v,s)*diff(phi[1](v,s),v));
W( e
−
1
2
sv
, e
1
2
sv
) := s (10.138)
Evaluation of the Green’s function
> G(x,v,s):=(phi[1](v,s)*phi[2](x,s)−phi[1](x,s)*phi[2](v,s))/W(phi[1](v,s),phi[2](v,s));
G(x∼,v,s):=
e
−
1
2
sv
e
1
2
sx∼
− e
−
1
2
sx∼
e
1
2
sv
s
(10.139)
Particular solution
> Up(x,s):=−Int(G(x,v,s)*(s*f(v)+g(v))/cˆ2,v);
Up(x ∼,s):= −
⎛
⎝
1
4
( e
−
1
2
sv
e
1
2
sx∼
− e
−
1
2
sx∼
e
1
2
sv
) sin(v)
s
dv
⎞
⎠
(10.140)
> Up(x,s):=simplify(subs(v=x,value(%)));
Up(x ∼,s):=
sin(x∼)
s
2
+4
(10.141)
General solution
> U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x)+Up(x,s);
U(x∼,s):= C1(s) e
−
1
2
sx∼
+C2(s) e
1
2
sx∼
+
sin(x∼)
s
2
+4
(10.142)
Substituting the boundary conditions at x = 0 and as x approaches infinity, for Re{s} > 0, we get
> C2(s):=0;
C2(s) := 0 (10.143)

Laplace Transform Methods for Partial Diff erential Equations 685
> eq:=Q(s)=eval(subs(x=0,U(x,s)));
eq := 0 = C1(s) (10.144)
> C1(s):=solve(eq,C1(s));
C1(s) := 0 (10.145)
Transformed solution for U(x, s)
> U(x,s):=eval(U(x,s));
U(x∼,s):=
sin(x∼)
s
2
+4
(10.146)
Solution is the inverse Laplace of U(x, s)
> u(x,t):=simplify(invlaplace(U(x,s),s,t));
u(x∼,t):=
1
2
sin(x∼) sin(2 t) (10.147)
ANIMATION
> animate(u(x,t),x=0..12,t=0..5,thickness=3);
The preceding animation command shows the spatial-time wave amplitude distribution u(x, t)
on the string. The animation sequence here and in Figure 10.11 shows snapshots of the
animation at times t = 0, 1, 2, 3, 4, 5.
ANIMATION SEQUENCE
> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):
> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):
> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):
> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..12,thickness=10);
0.1
0.2
0.3
0.4
0
24681012
2
0.1
2
0.2
2
0.3
2
0.4
x~
Figure 10.11

686 Chapter 10
EXAMPLE 10.7.6: (Longitudinal vibrations in a bar with impulse force) We consider
longitudinal wave motion in a bar over the semi-infinite interval I ={x |0 <x<∞}. The left
end of the bar is held fixed. Each cross section of the bar has the initial displacement
distribution f(x) = 0 and the initial speed distribution g(x) = 0. There is an applied impulse
force h(x, t), given following, acting on the bar at time t = 1. There is no damping in the
system, and the wave speed is c = 1.
SOLUTION: The nonhomogeneous wave partial differential equation is
∂
2
∂t
2
u(x, t) = c
2
∂
2
∂x
2
u(x, t)
+h(x, t)
The boundary conditions are
u(0,t)= 0 and u(∞,t)<∞
The initial conditions are
u(x, 0) = 0 and u
t
(x, 0) = 0
The Laplace transformed equation reads
∂
2
∂x
2
U(x, s) −
s
2
U(x, s)
c
2
=−
sf ( x )
c
2
−
g(x)
c
2
−
H(x, s)
c
2
Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary
conditions are
U(0,s)= Q(s) and U(∞,s)<∞
Assignment of system parameters
> restart:with(plots):with(inttrans):c:=1:q(t):=0:f(x):=0:f(v):=subs(x=v,f(x)):g(x):=0:
g(v):=subs(x=v,g(x)):h(x,t):=Dirac(t−1):
Transformed equation in x reads
> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2−H(x,s)/cˆ2;
∂
2
∂x
2
U(x, s) −s
2
U(x, s) =−H(x, s) (10.148)
Transformed boundary conditions
> Q(s):=Int(q(t)*exp(−s*t),t=0..infinity);
Q(s) :=
∞
0
0dt (10.149)

Laplace Transform Methods for Partial Diff erential Equations 687
> Q(s):=value(%);
Q(s) := 0 (10.150)
Transformed source term
> H(x,s):=Int(h(x,t)*exp(−s*t),t=0..infinity);
H(x, s) :=
∞
0
Dirac(t −1) e
−st
dt (10.151)
> H(x,s):=laplace(h(x,t),t,s);H(v,s):=subs(x=v,H(x,s)):
H(x, s) := e
−s
(10.152)
Basis vectors
> assume(x>0):phi[1](x,s):=exp(−s/c*x);phi[1](v,s):=subs(x=v,phi[1](x,s)):
phi[2](x,s):=exp(s/c*x);phi[2](v,s):=subs(x=v,phi[2](x,s)):
φ
1
(x∼,s):=e
−sx∼
φ
2
(x∼,s):=e
sx∼
(10.153)
Evaluation of the Wronskian
> W(phi[1](v,s),phi[2](v,s)):=simplify(phi[1](v,s)*diff(phi[2](v,s),v)−phi[2](v,s)*
diff(phi[1](v,s),v));
W( e
−sv
, e
sv
) := 2s (10.154)
Evaluation of the Green’s function
> G(x,v,s):=(phi[1](v,s)*phi[2](x,s)-phi[1](x,s)*phi[2](v,s))/W(phi[1](v,s),phi[2](v,s));
G(x∼,v,s):=
1
2
e
−sv
e
sx∼
− e
−sx∼
e
sv
s
(10.155)
Particular solution
> Up(x,s):=−Int(G(x,v,s)*(s*f(v)+g(v)+H(v,s))/cˆ2,v);
Up(x ∼,s):= −
1
2
( e
−sv
e
sx∼
− e
−sx∼
e
sv
) e
−s
s
dv
(10.156)
> Up(x,s):=simplify(subs(v=x,value(%)));
Up(x ∼,s):=
e
−s
s
2
(10.157)
