Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V

Подождите немного. Документ загружается.

688 Chapter 10

General solution

> U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x)+Up(x,s);

U(x∼,s):= C1(s) e

−sx∼

+C2(s) e

sx∼

−s

(10.158)

Substituting the boundary conditions at x = 0 and as x approaches inﬁnity, for Re{s} > 0,

we get

> C2(s):=0;

C2(s) := 0 (10.159)

> eq:=Q(s)=eval(subs(x=0,U(x,s)));

eq := 0 = C1(s) +

−s

(10.160)

> C1(s):=solve(eq,C1(s));

C1(s) := −

−s

(10.161)

Transformed solution for U(x, s)

> U(x,s):=eval(U(x,s));

U(x∼,s):= −

−s

−sx∼

−s

(10.162)

Solution is the inverse Laplace of U(x, s)

> u(x,t):=invlaplace(U(x,s),s,t);

u(x∼,t):= −Heaviside(t −1 −x∼)(t −1 −x∼) +Heaviside(t −1)(t −1) (10.163)

ANIMATION

> animate(u(x,t),x=0..12,t=0..5,thickness=3);

The preceding animation command shows the spatial-time wave amplitude distribution u(x, t)

in the bar. The animation sequence here and in Figure 10.12 shows snapshots of the animation

at times t = 0, 1, 2, 3, 4, 5.

ANIMATION SEQUENCE

> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):

> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):

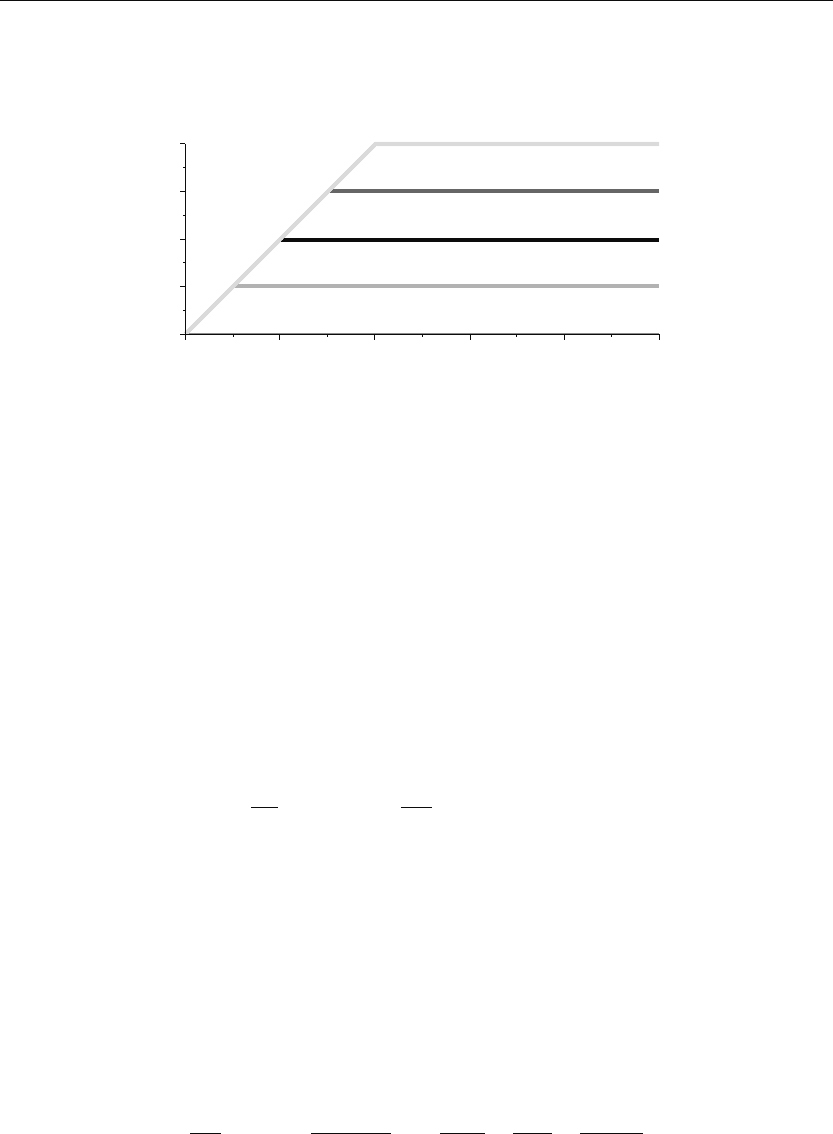
Laplace Transform Methods for Partial Diff erential Equations 689

> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):

> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..10,thickness=10);

0246810

Figure 10.12

Note that for times t<1, the longitudinal displacements of the bar are zero because the

impulse does not occur until time t = 1.

EXAMPLE 10.7.7: (String with external applied force) We seek the wave amplitude

u(x, t) for transverse wave motion along a taut string over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the string is held ﬁxed. The string has the initial

displacement distribution f(x) = 0 and the initial speed distribution g(x) = 0. An external

applied force h(x, t), given following, acts on the system. There is no damping in the system,

and the wave speed is c = 1.

SOLUTION: The nonhomogeneous wave partial differential equation is

∂

∂t

u(x, t) = c



∂

∂x

u(x, t)



+h(x, t)

The boundary conditions are

u(0,t)= 0 and u(∞,t)<∞

The initial conditions are

u(x, 0) = 0 and u

(x, 0) = 0

The Laplace transformed equation reads

∂

∂x

U(x, s) −

U(x, s)

=−

sf ( x )

−

g(x)

−

H(x, s)

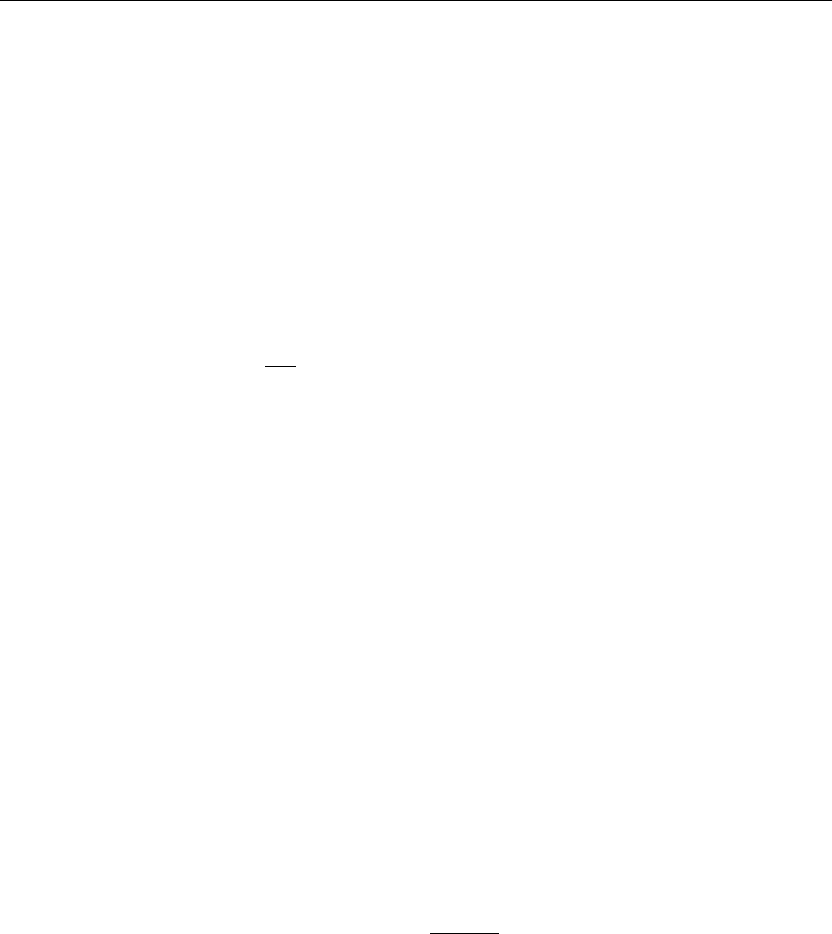
690 Chapter 10

Here, U(x, s) is the Laplace transform of u(x, t) with respect to t. The transformed boundary

conditions are

U(0,s)= Q(s) and U(∞,s)<∞

Assignment of system parameters

> restart:with(plots):with(inttrans):c:=1:q(t):=0:f(x):=0:f(v):=subs(x=v,f(x)):g(x):=0:

g(v):=subs(x=v,g(x)):h(x,t):=exp(−x)*t*exp(−t):

Transformed equation in x reads

> diff(U(x,s),x,x)−sˆ2/cˆ2*U(x,s)=−s*f(x)/cˆ2−g(x)/cˆ2−H(x,s)/cˆ2;

∂

∂x

U(x, s) −s

U(x, s) =−H(x, s) (10.164)

Transformed boundary conditions

> Q(s):=Int(q(t)*exp(−s*t),t=0..inﬁnity);

Q(s) :=

∞



0dt (10.165)

> Q(s):=value(%);

Q(s) := 0 (10.166)

Transformed source term

> H(x,s):=Int(h(x,t)*exp(−s*t),t=0..inﬁnity);

H(x, s) :=

∞



−x

t e

−t

−st

dt (10.167)

> H(x,s):=laplace(h(x,t),t,s);H(v,s):=subs(x=v,H(x,s)):

H(x, s) :=

−x

(1 +s)

(10.168)

Basis vectors

> assume(x>0):phi[1](x,s):=exp(−s/c*x);phi[1](v,s):=subs(x=v,phi[1](x,s)):

phi[2](x,s):=exp(s/c*x);phi[2](v,s):=subs(x=v,phi[2](x,s)):

(x∼,s):= e

−sx∼

(x∼,s):= e

sx∼

(10.169)

Laplace Transform Methods for Partial Diff erential Equations 691

Evaluation of the Wronskian

> W(phi[1](v,s),phi[2](v,s)):=simplify(phi[1](v,s)*diff(phi[2](v,s),v)

−phi[2](v,s)*diff(phi[1](v,s),v));

W( e

−sv

, e

) := 2s (10.170)

Evaluation of the Green’s function

> G(x,v,s):=(phi[1](v,s)*phi[2](x,s)−phi[1](x,s)*phi[2](v,s))/W(phi[1](v,s),phi[2](v,s));

G(x∼,v,s):=

−sv

sx∼

− e

−sx∼

(10.171)

Particular solution

> Up(x,s):=−Int(G(x,v,s)*(s*f(v)+g(v)+H(v,s))/cˆ2,v);

Up(x ∼,s):= −





( e

−sv

sx∼

− e

−sx∼

) e

−v

s(1 +s)



(10.172)

> Up(x,s):=simplify(subs(v=x,value(%)));

Up(x ∼,s):=

−x∼

(1 +s)

(−1 +s)

(10.173)

General solution

> U(x,s):=C1(s)*exp(−s/c*x)+C2(s)*exp(s/c*x)+Up(x,s);

U(x∼,s):= C1(s) e

−sx∼

+C2(s) e

sx∼

−x∼

(1 +s)

(−1 +s)

(10.174)

Substituting the boundary conditions at x = 0 and as x approaches inﬁnity, for Re{s} > 0,

we get

> C2(s):=0;

C2(s) := 0 (10.175)

> eq:=Q(s)=eval(subs(x=0,U(x,s)));

eq := 0 = C1(s) +

(1 +s)

(−1 +s)

(10.176)

> C1(s):=solve(eq,C1(s));

C1(s) := −

−1 −2s +2s

(10.177)

692 Chapter 10

Transformed solution for U(x, s)

> U(x,s):=eval(U(x,s));

U(x∼,s):= −

−sx∼

−1 −2 s +2s

−x∼

(1 +s)

(−1 +s)

(10.178)

Solution is the inverse Laplace of U(x, s)

> u(x,t):=invlaplace(U(x,s),s,t);

u(x∼,t):=

Heaviside(−t +x∼) e

t−x∼

−t+x∼

Heaviside(t −x∼)(2t

−4tx∼

+ 2x∼

+2t −2x∼+1) −

−x∼−t

(2t

+2t +1) (10.179)

ANIMATION

> animate(u(x,t),x=0..12,t=0..5,thickness=3);

The preceding animation command shows the spatial-time wave amplitude distribution u(x, t)

on the string. The animation sequence here and in Figure 10.13 shows snapshots of the

animation at times t = 0, 1, 2, 3, 4, 5.

ANIMATION SEQUENCE

> u(x,0):=subs(t=0,u(x,t)):u(x,1):=subs(t=1,u(x,t)):

> u(x,2):=subs(t=2,u(x,t)):u(x,3):=subs(t=3,u(x,t)):

> u(x,4):=subs(t=4,u(x,t)):u(x,5):=subs(t=5,u(x,t)):

> plot({u(x,0),u(x,1),u(x,2),u(x,3),u(x,4),u(x,5)},x=0..10,thickness=10);

0.20

0.15

0.10

0.05

246810

Figure 10.13

Laplace Transform Methods for Partial Diff erential Equations 693

Chapter Summary

Laplace transform of a piecewise continuous exponential-order function f(t)

F(s) =

∞



f(t) e

−st

Diffusion partial differential equation

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



+h(x, t)

Initial condition

u(x, 0) = f(x)

Laplace-transformed diffusion equation

∂

∂x

U(x, s) −

sU(x, s)

=−

f(x)

−

H(x, s)

Wave partial differential equation

∂

∂t

u(x, t) = c



∂

∂x

u(x, t)



+h(x, t)

Initial conditions

u(x, 0) = f(x) and u

(x, 0) = g(x)

Laplace-transformed wave equation

∂

∂x

U(x, s) −

U(x, s)

=−

sf ( x )

−

g(x)

−

H(x, s)

Transformed solution

U(x, s) =

∞



u(x, t) e

−st

Transformed source function

H(x, s) =

∞



h(x, t) e

−st

694 Chapter 10

Solution from inverse transform

u(x, t) =

a+i∞



a−i∞

U(x, s) e

2πi

Partitioned transform of solution

U(x, s) = U1(x, s)U2(x, s)

Convolution integral solution

u(x, t) =



u1(x, τ)u2(x, t −τ)dτ

where u1(x, t) is the inverse transform of U1(x, s) and u2(x, t) is the inverse transform of

U2(x, s).

In this chapter, we used the Laplace transform procedure for evaluating solutions to the

diffusion and the wave partial differential equations. The spatial domains of interest here were

semi-inﬁnite or inﬁnite. We did not consider Laplace transform methods on ﬁnite spatial

domains because these types of problems generally give rise to having to use the more

complicated methods of complex variables and residue theory to evaluate the inverse

tranforms. For ﬁnite domains, the eigenfunction methods covered in Chapters 3, 4, 6, 7, and 8

are generally much easier to implement.

Exercises

We now consider diffusion and wave equations in a single dimension over semi-inﬁnite

intervals with nonhomogeneous boundary conditions. The time variable of interest has the

domain {t |0 <t<∞}. Because of the possibility of a nonhomogeneous boundary condition,

the methods of Chapter 9 may fail here; thus, we use the Laplace transform method to solve

these types of problems. The Laplace transforms are taken with respect to the time variable t.

We do not consider problems over ﬁnite intervals here because the eigenfunction expansion

methods of earlier chapters are more convenient to use.

Laplace Transform Methods on the Diffusion Equation

We consider the temperature distribution along a thin rod whose lateral surface is insulated

over the semi-inﬁnite interval I ={x |0 <x<∞} for times {t |0 <t<∞}. We allow for an

Laplace Transform Methods for Partial Diff erential Equations 695

external heat source h(x, t) to act on the system. The nonhomogeneous diffusion partial

differential equation in rectangular coordinates in a single dimension reads

∂

∂t

u(x, t) = k



∂

∂x

u(x, t)



+h(x, t)

with the initial condition u(x, 0) = f(x).

For Exercises 10.1 through 10.20, we seek solutions to the preceding equation for various

given initial and boundary conditions. Evaluate the temperature distribution u(x, t) using the

Laplace transform method with respect to the variable t. Evaluate the inverse if possible;

otherwise, use the convolution method and leave the answer in the form of a convolution

integral. When possible, generate the animated solution for u(x, t), and plot the animated

sequence for 0 <t<5.

10.1. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

(0,t)= 0 and u(∞,t)<∞

Initial condition:

f(x) = e

−

10.2. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= 0 and u(∞,t)<∞

Initial condition:

f(x) = x e

−

10.3. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= 0 and u(∞,t)<∞

Initial condition:

f(x) = sin(x)

696 Chapter 10

10.4. Consider a thin cylinder over the semi-inﬁnite interval I ={x |0 <x<∞}

containing a ﬂuid that has an initial salt concentration density given as f(x). There is

no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= 0 and u(∞,t)<∞

Initial condition:

f(x) = Dirac(x −1)

10.5. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The initial temperature distribution in the rod is given as f(x).

There is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= 0 and u(∞,t)<∞

Initial condition:

f(x) = sin(x) e

−x

10.6. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the rod is constrained to a temperature

u(0,t)= q(t) given following. The initial temperature distribution in the rod is 0,

there is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= 5 and u(∞,t)<∞

Initial condition:

f(x) = 0

10.7. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the rod is constrained to the temperature

u(0,t)= q(t) given following. The initial temperature distribution in the rod is 0,

there is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= sin(t) and u(∞,t)<∞

Initial condition:

f(x) = 0

Laplace Transform Methods for Partial Diff erential Equations 697

10.8. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the rod is constrained to the temperature

u(0,t)= q(t) given following. The initial temperature distribution in the rod is 0,

there is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= e

−t

and u(∞,t)<∞

Initial condition:

f(x) = 0

10.9. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the rod is constrained to a temperature

u(0,t)= q(t) given following. The initial temperature distribution in the rod is 0,

there is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= t e

−t

and u(∞,t)<∞

Initial condition:

f(x) = 0

10.10. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the rod is constrained to the temperature

u(0,t)= q(t) given following. The initial temperature distribution in the rod is 0,

there is no source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

u(0,t)= sin(t) e

−t

and u(∞,t)<∞

Initial condition:

f(x) = 0

10.11. Consider a thin rod whose lateral surface is insulated over the semi-inﬁnite interval

I ={x |0 <x<∞}. The left end of the rod has the input heat ﬂux u

(0,t)= q(t)

given following. The initial temperature distribution in the rod is 0, there is no

source term in the system, and the diffusivity has the magnitude k = 1/4.

Boundary conditions:

(0,t)=−5 and u(∞,t)<∞

Initial condition:

f(x) = 0