Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.

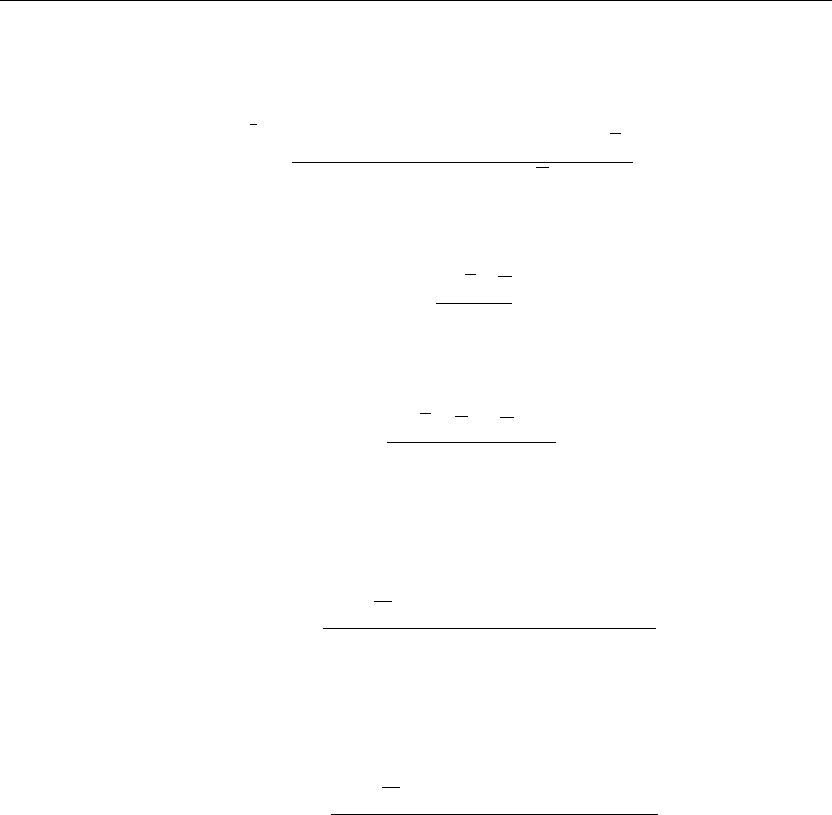
378 Chapter 6
Evaluation of the Fourier coefficients yields
> C(1,n):=Int(Int(f(r,theta)*R[1,n](r)*w(r)*Theta[1](theta)*w(theta),r=0..a),theta=0..b);
C(1,n):=
1
2
π
0
1
0
2(r −r
3
) sin(θ)
2
BesselJ(1,λ
1,n
r)
√
2 r
BesselJ(0,λ
1,n
)
√
π
dr dθ (6.77)
> C(1,n):=radsimp(subs(BesselJ(1,lambda[1,n]*a)=0,value(%)));
C(1,n):= −
4
√
2
√
π
λ
3
1,n
(6.78)
> T[1,n](t):=eval(subs(m=1,T[m,n](t)));
T
1,n
(t) := −
4
√
2
√
π e
−
1
50
λ
2
1,n
t
λ
3
1,n
(6.79)
Generalized series terms
> u[1,n](r,theta,t):=(T[1,n](t)*R[1,n](r)*Theta[1](theta));
u
1,n
(r,θ,t):= −
16 e
−
1
50
λ
2
1,n
t
BesselJ(1,λ
1,n
r) sin(θ)
λ
3
1,n
BesselJ(0,λ
1,n
)
(6.80)
Series solution
> u(r,theta,t):=Sum(u[1,n](r,theta,t),n=1..infinity);
u(r,θ,t):=
∞
n=1
⎛
⎝
−
16 e
−
1
50
λ
2
1,n
t
BesselJ(1,λ
1,n
r) sin(θ)
λ
3
1,n
BesselJ(0,λ
1,n
)
⎞
⎠
(6.81)
Evaluation of the eigenvalues λ
1,n
from the roots of the eigenvalue equation yields
> subs({m=1,r=a},BesselJ(mu[m],lambda[m,n]*r))=0;
BesselJ(1,λ
1,n
) = 0 (6.82)
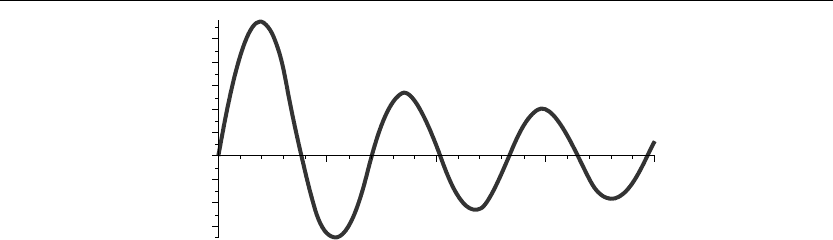
> plot(BesselJ(1,v),v=0..20,thickness=10);
If we set v = λa, then the eigenvalues λ
1,n
are found from the intersection points of the curve
of J(1,v) with the v-axis shown in Figure 6.9. Using the Maple fsolve command to evaluate
the first few eigenvalues yields
The Diffusion Equation in Two Spatial Dimensions 379
5
0.5
0.4
0.3
0.2
0.1
20.1
20.2
20.3
0
10
v
15 20
Figure 6.9
> lambda[1,1]:=(1/a)*fsolve(BesselJ(1,v)=0,v=1..6);
λ
1,1
:= 3.831705970 (6.83)
> lambda[1,2]:=(1/a)*fsolve(BesselJ(1,v)=0,v=6..9);
λ
1,2
:= 7.015586670 (6.84)
> lambda[1,3]:=(1/a)*fsolve(BesselJ(1,v)=0,v=9..12);
λ
1,3
:= 10.17346814 (6.85)
First few terms in sum
> u(r,theta,t):=sum(u[1,n](r,theta,t),n=1..3):
ANIMATION
> u(x,y,t):=subs({r=sqrt(xˆ2+yˆ2),theta=arctan(y/x)},u(r,theta,t))*Heaviside(1−sqrt(xˆ2+yˆ2)):
> animate3d(u(x,y,t),x=0..a,y=0..a,t=0..8,axes=framed,thickness=1);
The preceding animation command illustrates the spatial-time-dependent solution for u(r,θ,t).
The animation sequence in Figures 6.10 and 6.11 shows snapshots of the animation at the two
different times t = 0 and t = 3.
ANIMATION SEQUENCE
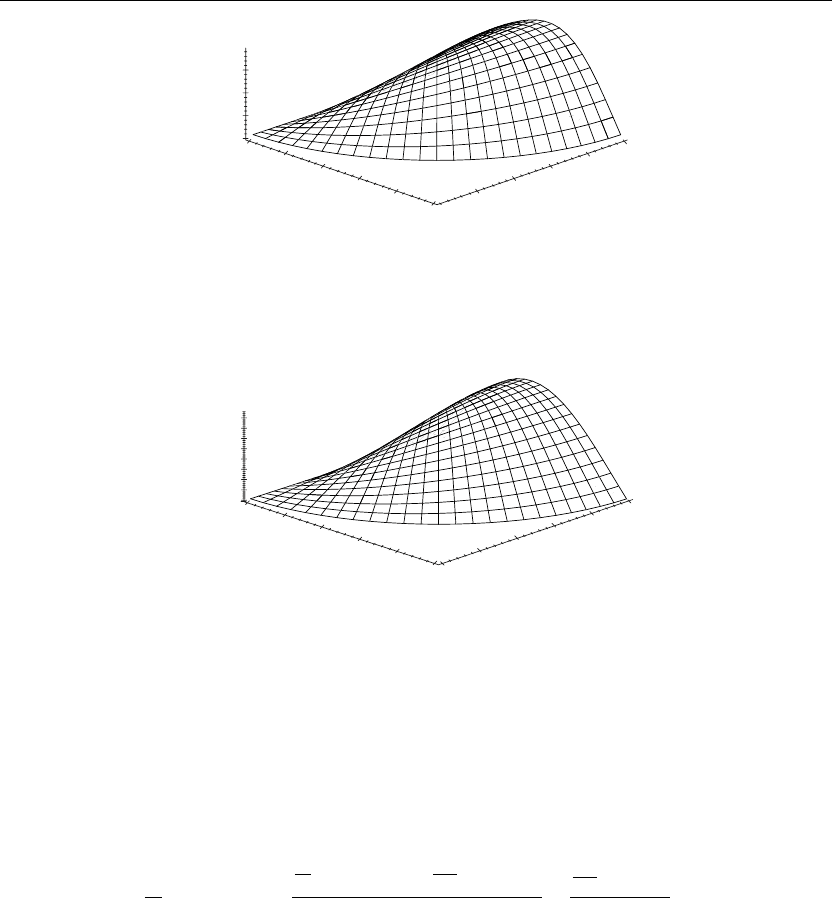
> u(r,theta,0):=subs(t=0,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,0)],r=0..a,theta=0..b,
axes=framed,thickness=1);
380 Chapter 6
0.3
0.2
0.1
0
0
0.2
0.4
0.6
0.8
0.8
0.6
0.4
0.2
0
1
1
z
y
x
Figure 6.10
> u(r,theta,3):=subs(t=3,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,3)],r=0..a,theta=0..b,
axes=framed,thickness=1);
0.16
0.12
0.08
0.04
0
0
0.2
0.4
0.6
0.8
0.8
0.6
0.4
0.2
0
1
1
z
y
x
Figure 6.11
EXAMPLE 6.9.2: We seek the temperature distribution in a thin circular plate over the
two-dimensional domain D ={(r, θ) |0 <r<1, 0 <θ<π}. The lateral surfaces of the plate
are insulated. The sides θ = 0 and θ = π are at a fixed temperature of 0, and the edge r = 1is
insulated. The initial temperature distribution u(r, θ, 0) = f(r, θ) is given as follows, and the
thermal diffusivity is k = 1/25.
SOLUTION: The two-dimensional homogeneous diffusion equation is
∂
∂t
u(r,θ,t)= k
⎛
⎝
∂
∂r
u(r,θ,t)+r
∂
2
∂r
2
u(r,θ,t)
r
+
∂
2
∂θ
2
u(r,θ,t)
r
2
⎞
⎠
The boundary conditions are type 2 at r = 1, type 1 at θ = 0, and type 1 at θ = π and a finite
solution at the origin:
|u(0,θ,t)| < ∞ and u
r
(1,θ,t)= 0
and
u(r, 0,t)= 0 and u(r,π,t)= 0

The Diffusion Equation in Two Spatial Dimensions 381
The initial condition is
u(r, θ, 0) =
r −
r
3
3
sin(θ)
The ordinary differential equations from the method of separation of variables are
d
dt
T(t) +kλ
2
T(t) = 0
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
+
λ
2
r
2
−μ
2
R(r) = 0
d
2
dθ
2
(θ)+μ
2
(θ) = 0
The boundary conditions on the spatial variables are
|R(0)| < ∞ and R
r
(1) = 0
and
(0) = 0 and (π) = 0
Assignment of system parameters
> restart:with(plots):a:=1:b:=Pi:k:=1/25:
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Examples 2.5.1 and 2.6.3.
> mu[m]:=m*Pi/b;
μ
m
:= m (6.86)
for m = 1, 2, 3,....
Eigenvalues λ
m,n
are the roots of the eigenvalue equation
> subs(r=a,diff(BesselJ(mu[m],lambda[m,n]*r),r))=0;
−BesselJ(m +1,λ
m,n
) +
mBesselJ(m, λ
m,n
)
λ
m,n
λ
m,n
= 0 (6.87)
for m = 1, 2, 3,..., n= 1, 2, 3,....
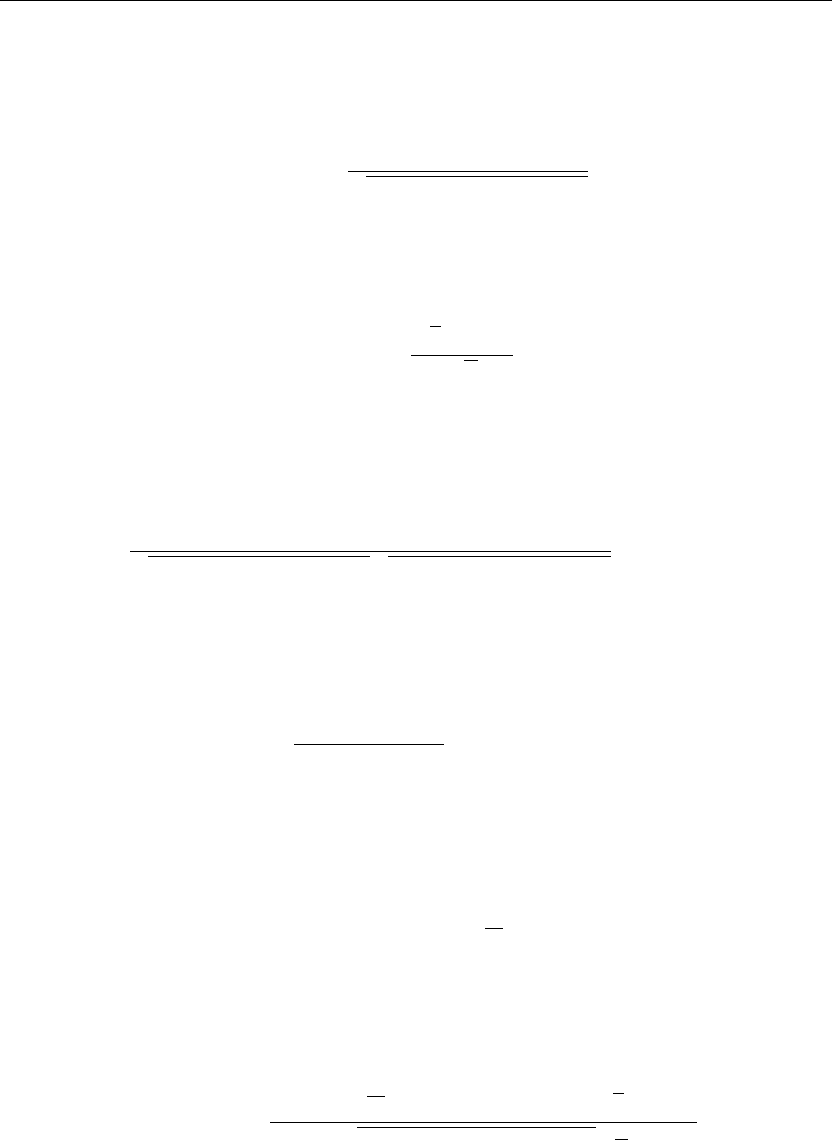
382 Chapter 6
Orthonormal eigenfunctions
> R[m,n](r):=BesselJ(mu[m],lambda[m,n]*r)/sqrt(Int(BesselJ(mu[m],lambda[m,n]*r)ˆ2*r,
r=0..a));R[m,p](r):=subs(n=p,R[m,n](r)):
R
m,n
(r) :=
BesselJ(m, λ
m,n
r)
1
0
BesselJ(m, λ
m,n
r)
2
r dr
(6.88)
> Theta[m](theta):=sqrt(2/b)*sin(m*Pi/b*theta);Theta[q](theta):=subs(m=q,Theta[m](theta)):
m
(θ) :=
√
2 sin(mθ)
√
π
(6.89)
Statements of orthonormality with their respective weight functions
> w(r):=r:Int(R[m,n](r)*R[m,p](r)*w(r),r=0...a)=delta(n,p);
1
0
BesselJ(m, λ
m,n
r)BesselJ(m, λ
m,p
r)r
1
0
BesselJ(m, λ
m,n
r)
2
r dr
1
0
BesselJ(m, λ
m,p
r)
2
r dr
dr = δ(n, p) (6.90)
> w(theta):=1:Int(Theta[m](theta)*Theta[q](theta)*w(theta),theta=0...b)=delta(m,q);
π
0
2 sin(mθ) sin(qθ)
π
dθ = δ(m, q) (6.91)
Time-dependent solution
> T[m,n](t):=C(m,n)*exp(−k*lambda[m,n]ˆ2*t);
T
m,n
(t) := C(m, n) e
−
1
25
λ
2
m,n
t
(6.92)
Generalized series terms
> u[m,n](r,theta,t):=T[m,n](t)*R[m,n](r)*Theta[m](theta);
u
m,n
(r,θ,t):=
C(m, n)e
−
1
25
λ
2
m,n
t
BesselJ(m, λ
m,n
r)
√
2 sin(mθ)
1
0
BesselJ(m, λ
m,n
r)
2
r dr
√
π
(6.93)

The Diffusion Equation in Two Spatial Dimensions 383
Eigenfunction expansion
> u(r,theta,t):=Sum(Sum(u[m,n](r,theta,t),m=0..infinity),n=0..infinity);
u(r,θ,t):=
∞
n=0
⎛
⎜
⎝
∞
m=0
C(m, n)e
−
1
25
λ
2
m,n
t
BesselJ(m, λ
m,n
r)
√
2 sin(mθ)
1
0
BesselJ(m, λ
m,n
r)
2
r dr
√
π
⎞
⎟
⎠
(6.94)
The Fourier coefficients C(m, n) are to be determined from the initial condition function
u(r, θ, 0) = f(r, θ). We consider the special case where
> f(r,theta):=(r−rˆ3/3)*sin(theta);
f(r, θ) :=
r −
1
3
r
3
sin(θ) (6.95)
At time t = 0, we have
> f(r,theta)=eval(subs(t=0,u(r,theta,t)));
r −
1
3
r
3
sin(θ) =
∞
n=0
⎛
⎜
⎝
∞
m=0
C(m, n)BesselJ(m, λ
m,n
r)
√
2 sin(mθ)
1
0
BesselJ(m, λ
m,n
r)
2
rdr
√
π
⎞
⎟
⎠
(6.96)
This is the double Fourier series expansion of f(r, θ). From Section 6.8, the Fourier coefficients
C
(
m, n
)
were evaluated by taking the double inner product of the initial condition function
f(r, θ) with respect to the preceding corresponding orthonormalized eigenfunctions.
Because f(r, θ) depends on sin(mθ) for the m = 1 case, then, from the given orthogonality
statement for θ, only the m = 1 solution survives here, and we set
> Theta[1](theta):=subs(m=1,eval(Theta[m](theta)));
1
(θ) :=
√
2 sin(θ)
√
π
(6.97)
Eigenvalues λ
1,n
are the roots of the eigenvalue equation
> subs({m=1,r=a},diff(BesselJ(mu[m],lambda[m,n]*r),r))=0;
−BesselJ(2,λ
1,n
) +
BesselJ(1,λ
1,n
)
λ
1,n
λ
1,n
= 0 (6.98)
For m = 1, we have the Bessel identity
> subs(m=1,BesselJ(m−1,lambda[m,n]*a)=2*m*BesselJ(m,lambda[m,n]*a)/(lambda[m,n]*a)
−BesselJ(m+1,lambda[m,n]*a));
BesselJ(0,λ
1,n
) =
2BesselJ(1,λ
1,n
)
λ
1,n
−BesselJ(2,λ
1,n
) (6.99)

384 Chapter 6
Evaluation of the orthonormalized eigenfunctions for m=1
> R[1,n](r):=eval(subs(m=1,BesselJ(mu[m],lambda[m,n]*r)/sqrt(expand(int(subs(m=1,
BesselJ(mu[m],lambda[m,n]*r))ˆ2*r,r=0..a)))));
R
1,n
(r) :=
2BesselJ(1,λ
1,n
r)
2 BesselJ(0,λ
1,n
)
2
−
4 BesselJ(0,λ
1,n
) BesselJ(1,λ
1,n
)
λ
1,n
+2 BesselJ(1,λ
1,n
)
2
(6.100)
Substitution of the preceding eigenvalue equation and the Bessel identity simplifies this to
> R[1,n](r):=radsimp(subs(BesselJ(0,lambda[1,n]*a)=BesselJ(1,lambda[1,n]*a)/(lambda[1,n]
*a),R[1,n](r)));
R
1,n
(r) :=
BesselJ(1,λ
1,n
r)
√
2λ
1,n
BesselJ(1,λ
1,n
)
−1 +λ
2
1,n
(6.101)
Evaluation of the Fourier coefficients yields
> C(1,n):=Int(Int(f(r,theta)*R[1,n](r)*w(r)*Theta[1](theta)*w(theta),r=0..a),theta=0..b);
C(1,n):=
π
0
1
0
2
r −
1
3
r
3
sin(θ)
2
BesselJ(1,λ
1,n
r)λ
1,n
r
BesselJ(1,λ
1,n
)
−1 +λ
2
1,n
√
π
dr dθ (6.102)
> C(1,n):=simplify(subs(BesselJ(0,lambda[1,n]*a)=BesselJ(1,lambda[1,n]*a)/
(lambda[1,n]*a),value(%)));
C(1,n):=
8
3
√
π
λ
3
1,n
−1 +λ
2
1,n
(6.103)
> T[1,n](t):=eval(subs(m=1,T[m,n](t)));
T
1,n
(t) :=
8
3
√
π e
−
1
25
λ
2
1,n
t
λ
3
1,n
−1 +λ
2
1,n
(6.104)
Generalized series terms
> u[1,n](r,theta,t):=T[1,n](t)*R[1,n](r)*Theta[1](theta);
u
1,n
(r,θ,t):=
16
3
e
−
1
25
λ
2
1,n
t
BesselJ(1,λ
1,n
r) sin(θ)
λ
2
1,n
−1 +λ
2
1,n
BesselJ(1,λ
1,n
)
(6.105)
The Diffusion Equation in Two Spatial Dimensions 385
Series solution
> u(r,theta,t):=Sum(u[1,n](r,theta,t),n=1..infinity);
u(r,θ,t):=
∞
n=1
16
3
e
−
1
25
λ
2
1,n
t
BesselJ(1,λ
1,n
r) sin(θ)
λ
2
1,n
−1 +λ
2
1,n
BesselJ(1,λ
1,n
)
(6.106)
Evaluation of the eigenvalues λ
1,n
from the eigenvalue equation yields
> subs({m=1,r=a},diff(BesselJ(mu[m],lambda[m,n]*r),r))=0;
−BesselJ(2,λ
1,n
) +
BesselJ(1,λ
1,n
)
λ
1,n
λ
1,n
= 0 (6.107)
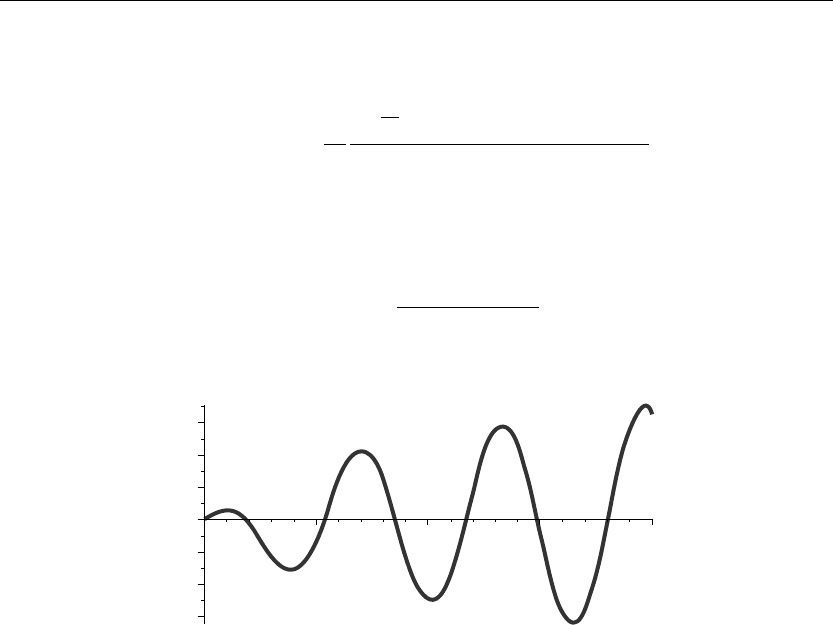
> plot(BesselJ(1,v)−v*BesselJ(2,v),v=0..20,thickness=10);
5
3
2
1
21
22
23
0
10
v
15 20
Figure 6.12
If we set v = λa, then the eigenvalues are found from the intersection points of the curve
J(1,v)−vJ(2,v) with the v-axis shown in Figure 6.12. Using the Maple fsolve command to
evaluate the first few eigenvalues yields
> lambda[1,1]:=(1/a)*fsolve(BesselJ(1,v)−v*BesselJ(2,v)=0,v=1..4);
λ
1,1
:= 1.841183781 (6.108)
> lambda[1,2]:=(1/a)*fsolve(BesselJ(1,v)−v*BesselJ(2,v)=0,v=4..7);
λ
1,2
:= 5.331442774 (6.109)
> lambda[1,3]:=(1/a)*fsolve(BesselJ(1,v)−v*BesselJ(2,v)=0,v=7..11);
λ
1,3
:= 8.536316366 (6.110)
Note that we ignore the root λ = 0, since it leads to a trivial solution.
First few terms in sum
> u(r,theta,t):=sum(u[1,n](r,theta,t),n=1..2):
386 Chapter 6
ANIMATION
> u(x,y,t):=subs({r=sqrt(xˆ2+yˆ2),theta=arcsin(y/sqrt(xˆ2+yˆ2))},u(r,theta,t))*
Heaviside(1−sqrt(xˆ2+yˆ2)):
> animate3d(u(x,y,t),x=−a..a,y=0..a,t=0..8,axes=framed,thickness=1);
The preceding animation command illustrates the spatial-time-dependent solution for u(r,θ,t).
The animation sequence in Figures 6.13 and 6.14 shows snapshots of the animation at the two
different times t = 0 and t = 5.
ANIMATION SEQUENCE
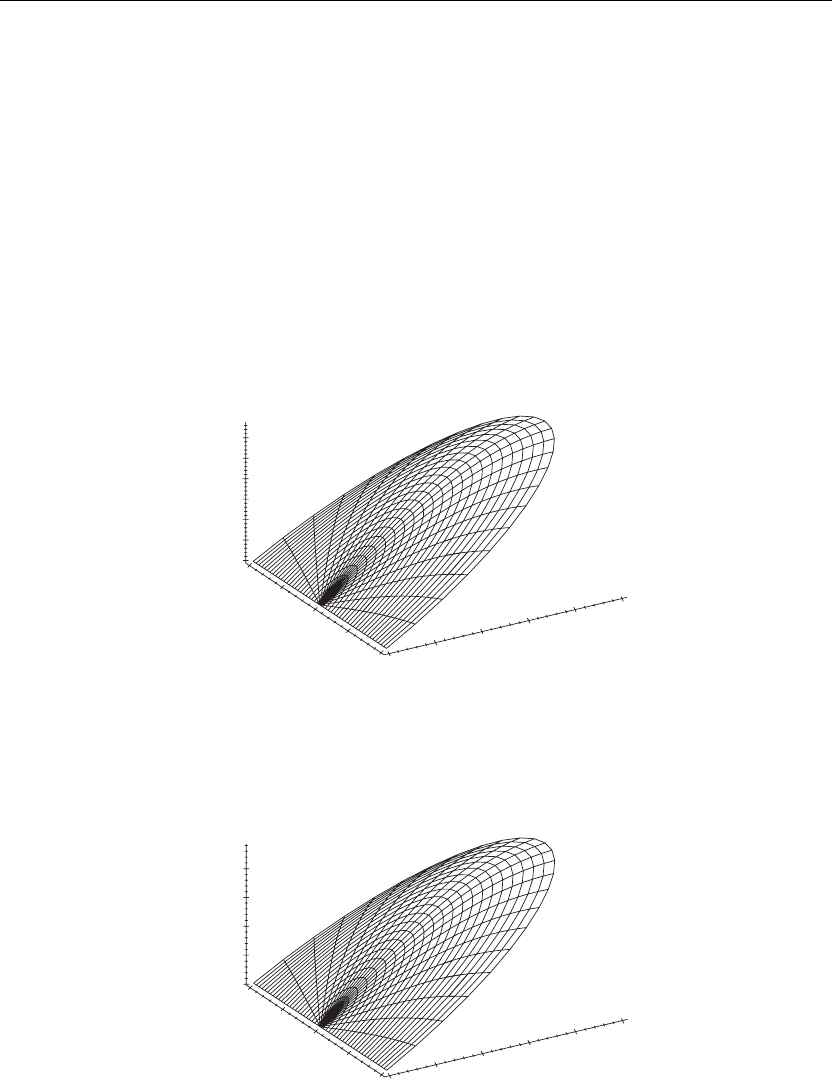
> u(r,theta,0):=subs(t=0,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,0)],r=0..a,theta=0..b,
axes=framed,thickness=1);
0.6
0.6
y
x
0.8
1
0.5
0.4
0.4
0.3
0.2
0.2
0.1
0
21
20.5
0
0
0.5
1
z
Figure 6.13
> u(r,theta,5):=subs(t=5,u(r,theta,t)):cylinderplot([r,theta,u(r,theta,5)],r=0..a,theta=0..b,
axes=framed,thickness=1);
0.6
y
x
0.8
1
0.4
0.4
0.3
0.2
0.2
0.1
0
21
20.5
0
0
0.5
1
z
Figure 6.14

The Diffusion Equation in Two Spatial Dimensions 387
EXAMPLE 6.9.3: We consider the temperature distribution in a thin circular plate over the
two-dimensional domain D ={(r, θ) |0 <r<1, −π<θ<π}. The lateral surfaces of the plate
are insulated. The periphery r = 1 is held at a fixed temperature of 0, and the θ-dependent
solution satisfies periodic boundary conditions. The initial temperature distribution
u(r, θ, 0) = f(r, θ) is given as follows, and the thermal diffusivity is k = 1/50.
SOLUTION: The two-dimensional homogeneous diffusion equation is
∂
∂t
u(r,θ,t)= k
⎛
⎝
∂
∂r
u(r,θ,t)+r
∂
2
∂r
2
u(r,θ,t)
r
+
∂
2
∂θ
2
u(r,θ,t)
r
2
⎞
⎠
The boundary conditions are type 1 at r = 1, a finite solution at the origin, and periodic
boundary conditions on θ:
|u(0,θ,t)| < ∞ and u(1,θ,t)= 0
and
u(r, −π, t) = u(r,π,t) and u
θ
(r, −π, t) = u
θ
(r,π,t)
The initial condition is
u(r, θ, 0) =
r
2
−r
4
sin(2 θ)
The ordinary differential equations from the method of separation of variables are
d
dt
T(t) +kλ
2
T(t) = 0
r
2
d
2
dr
2
R(r)
+r
d
dr
R(r)
+
λ
2
r
2
−μ
2
R(r) = 0
d
2
dθ
2
(θ)+μ
2
(θ) = 0
The boundary conditions on the spatial variables are
|R(0)| < ∞ and R(1) = 0
and
(−π) = (π) and
θ
(−π) =
θ
(π)
Assignment of system parameters
> restart:with(plots):a:=1:b:=Pi:k:=1/50:
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Examples 2.6.1 and 2.6.2.
