Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


348 Chapter 6
at time t = 0 yields
f(x, y) =
∞
n=0
∞
m=0
C(m, n)X
m
(x)Y
n
(y)
Because the eigenfunctions of the regular Sturm-Liouville problem form a complete set with
respect to piecewise smooth functions over the finite two-dimensional domain, the preceding is
the generalized double Fourier series expansion of the function f(x, y) in terms of the allowed
eigenfunctions and the double Fourier coefficients C(m, n). We now evaluate these coefficients.
As we did in Chapter 2, Section 2.4 for the generalized Fourier series expansion, we take the
double inner products of both sides of the preceding equation, with respect to the x- and
y-dependent eigenfunctions, and this yields
b
0
a
0
f(x, y)X
r
(x)Y
s
(y) dx dy =
b
0
a
0
∞
n=0
∞
m=0
C(m, n)X
m
(x)Y
n
(y)
X
r
(x) Y
s
(y) dx dy
If we assume the necessary conditions of uniform convergence of the series to ensure the
validity of the interchange between the integration operators and the summation operators, then
the double inner products of both sides of this equation can be written as
b
0
a
0
f(x, y)X
r
(x) Y
s
(y) dx dy =
∞
n=0
⎛
⎝
∞
m=0
C(m, n)
⎛
⎝
a
0
X
m
(x)X
r
(x) dx
⎞
⎠
⎛
⎝
b
0
Y
n
(y) Y
s
(y) dy
⎞
⎠
⎞
⎠
Taking advantage of the statements of orthonormality for the two integrals on the right yields
b
0
a
0
f(x, y) X
r
(x)Y
s
(y) dx dy =
∞
n=0
∞
m=0
C(m, n)δ(m, r)δ(n, s)
Due to the mathematical nature of the Kronecker delta functions, the double sum on the right is
easy to determine (only the m = r, n = s term survives), and the double Fourier coefficients
C(m, n) are evaluated to be
C(m, n) =
b
0
a
0
f(x, y)X
m
(x)Y
n
(y) dx dy (6.1)
We now demonstrate an example for evaluating these coefficients.
DEMONSTRATION: We seek the solution to the example problem in Section 6.4 for the
special case where the initial temperature distribution is u(x, y, 0) = f(x, y) where
f(x, y) =
1 −
x
2
3
y(1 −y)
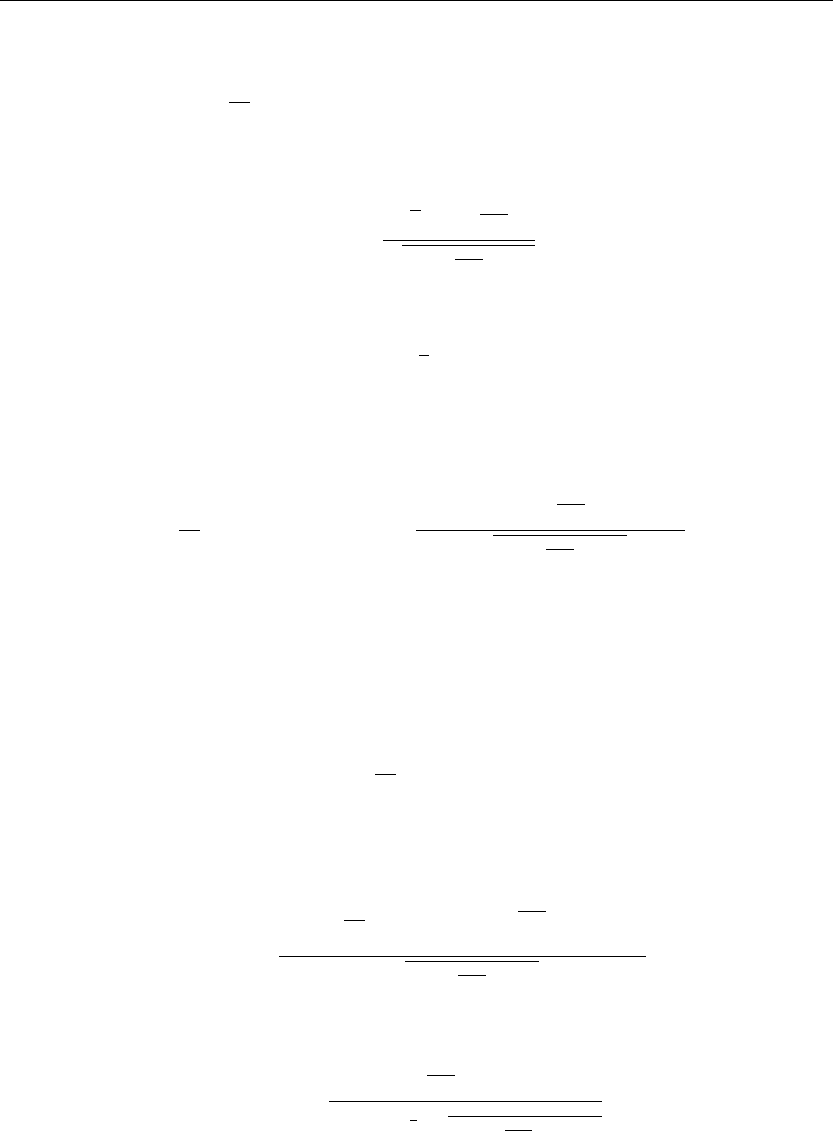
The Diffusion Equation in Two Spatial Dimensions 349
SOLUTION: Substituting t = 0 in the solution for u(x, y, t) yields
1 −
x
2
3
y(1 −y) =
∞
n=0
∞
m=0
C(m, n)X
m
(x)Y
n
(y)
where, from the preceding example, the orthonormalized eigenfunctions are
X
m
(x) =
√
2 cos
√
α
m
x
sin
√
α
m
2
+1
and
Y
n
(y) =
√
2 sin(nπy)
for m = 1, 2, 3,..., and n = 1, 2, 3,.... Insertion of these eigenfunctions into the above series
yields
1 −
x
2
3
y(1 −y) =
∞
n=0
⎛
⎜
⎝
∞
m=0
2C(m, n) cos
√
α
m
x
sin(nπy)
sin
√
α
m
2
+1
⎞
⎟
⎠
This is the double Fourier series expansion of f(x, y) in terms of the evaluated eigenfunctions
from Section 6.4. The Fourier coefficients C(m, n) were evaluated by taking the double inner
product of the initial condition function f(x, y) with respect to these corresponding
orthonormalized eigenfunctions. Doing so yielded the integral
C(m, n) =
1
0
1
0
1 −
x
2
3
y(1 −y)X
m
(x)Y
n
(y) dx dy
which, for the preceding eigenfunctions, reduces to
C(m, n) =
1
0
1
0
2
1 −
x
2
3
y(1 −y) cos
√
α
m
x
sin(nπy)
sin
√
α
m
2
+1
dx dy
for n = 1, 2, 3,..., and m = 1, 2, 3,.... Evaluation of this integral yields
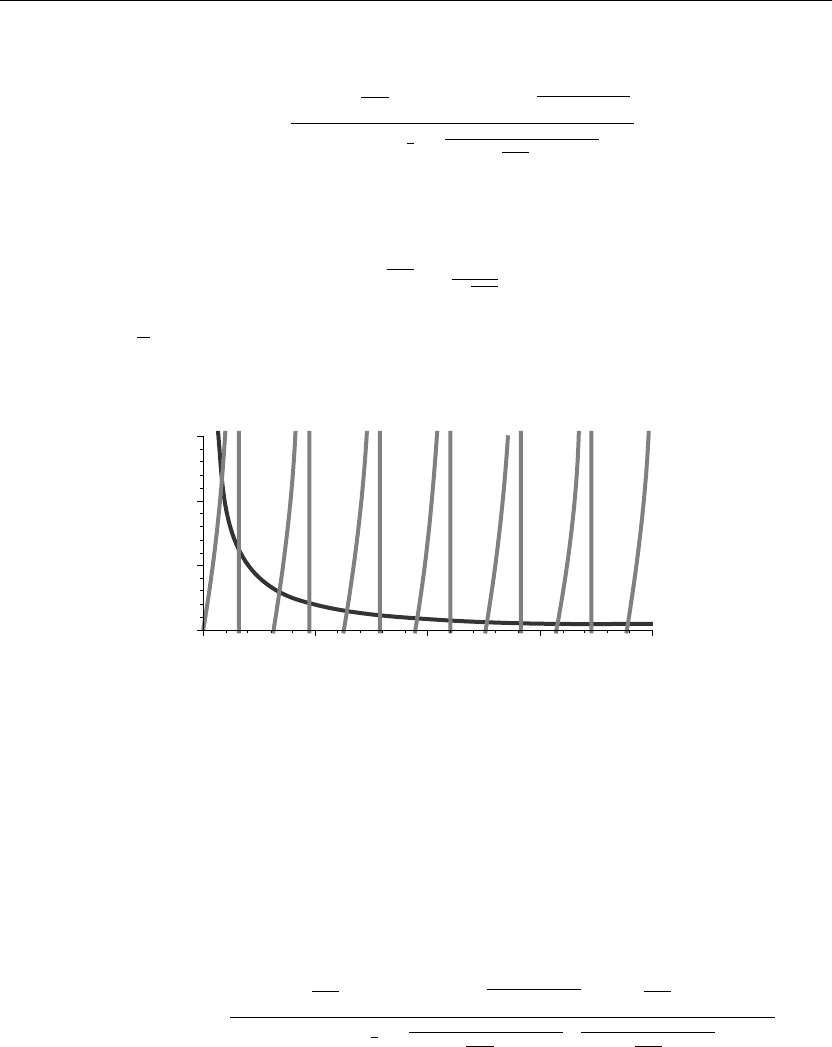
C(m, n) =
8 cos
√
α
m
1 −(−1)
n
3n
3
π
3
α
3
2
m
cos
√
α
m
2
+α
m
350 Chapter 6
Thus, the time-dependent solution becomes
T
m,n
(t) =
8 cos
√
α
m
1 −(−1)
n
e
−
α
m
+n
2
π
2
t
10
3n
3
π
3
α
3
2
m
cos
√
α
m
2
+α
m
The eigenvalues α
m
are determined from the roots of the equation
tan
√
α
m
=
1
√
α
m
(6.2)
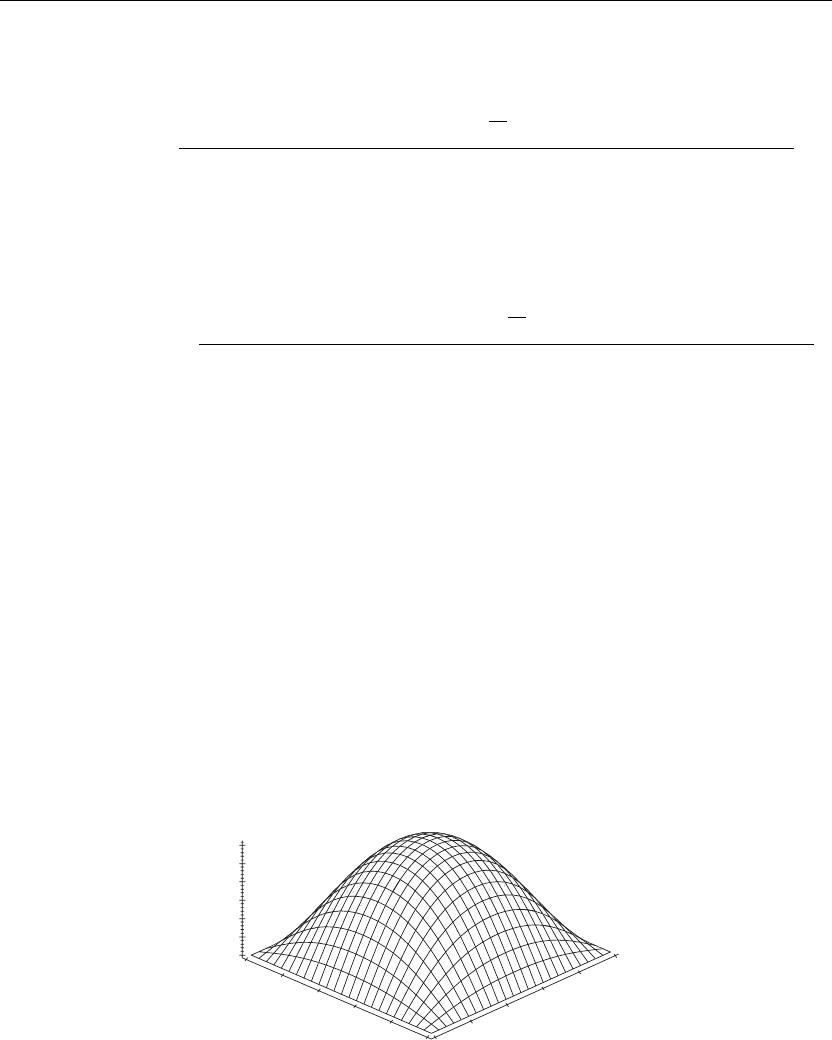
If we set v =
√
α, then the eigenvalues α
m
are given as the squares of the values at the
intersection points of the curves tan(v) and 1/v shown in Figure 6.1.
0
0
0.5
1
1.5
5101520
Figure 6.1
The first three eigenvalues are
α
1
= 0.74017
α
2
= 11.7348
α
3
= 41.4388
With knowledge of the eigenvalues α
m
, the final series solution to the problem is
u(x, y, t) =
∞
n=1
⎛
⎜
⎜
⎝
∞
n=1
16 cos
√
α
m
1 −(−1)
n
e
−
α
m
+n
2
π
2
t
10
cos
√
α
m
x
sin(nπy)
3n
3
π
3
α
3
2
m
cos
√
α
m
2
+α
m
sin
√
α
m
2
+1
⎞
⎟
⎟
⎠
The details for the development of this solution and the graphics are given later in one of the
Maple worksheet examples.

The Diffusion Equation in Two Spatial Dimensions 351
6.6 Example Diffusion Problems in Rectangular
Coordinates
We now consider several examples of partial differential equations for heat or diffusion
phenomena under various homogeneous boundary conditions over finite two-dimensional
domains in the rectangular coordinate system. We note that all the spatial ordinary differential
equations are of the Euler type.
EXAMPLE 6.6.1: We seek the temperature distribution in a thin rectangular plate over the
finite two-dimensional domain D ={(x, y) |0 <x<1, 0 <y<1}. The lateral surfaces of the
plate are insulated. The boundaries are all fixed at temperature 0, the plate has an initial
temperature distribution f(x, y) given as follows, and the thermal diffusivity is k = 1/80.
SOLUTION: The two-dimensional homogeneous diffusion equation is
∂
∂t
u(x, y, t) = k
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
The boundary conditions are type 1 at x =0, type 1 at x =1, type 1 at y = 0, and type 1 at y =1:
u(0,y,t)= 0 and u(1,y,t)= 0
and
u(x, 0,t)= 0 and u(x, 1,t)= 0
The initial condition is
u(x, y, 0) = x(1 −x)y(1 −y)
The ordinary differential equations from the method of separation of variables are
d
dt
T(t) +kλT(t) = 0
d
2
dx
2
X(x)+αX(x)= 0
d
2
dy
2
Y(y) +βY(y)= 0
The coupling equation reads
λ = α +β
T he boundary conditions on the spatial variables are
X(0) = 0,X(1) = 0

352 Chapter 6
and
Y(0) = 0,Y(1) = 0
Assignment of system parameters
> restart:with(plots):a:=1:b:=1:k:=1/80:
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Example 2.5.1.
> alpha[m]:=(m*Pi/a)ˆ2;beta[n]:=(n*Pi/b)ˆ2;lambda[m,n]:=alpha[m]+beta[n];
α
m
:= m
2
π
2
β
n
:= n
2
π
2
λ
m,n
:= m
2
π
2
+n
2
π
2
(6.3)
for m = 1, 2, 3,...,n= 1, 2, 3,....
Orthonormal eigenfunctions
> X[m](x):=sqrt(2/a)*sin(m*Pi/a*x);X[r](x):=subs(m=r,X[m](x)):
X
m
(x) :=
√
2 sin(mπx) (6.4)
> Y[n](y):=sqrt(2/b)*sin(n*Pi/b*y);Y[s](y):=subs(n=s,Y[n](y)):
Y
n
(y) :=
√
2 sin(nπy) (6.5)
Statements of orthonormality with their respective weight functions
> w(x):=1:Int(X[m](x)*X[r](x)*w(x),x=0...a)=delta(m,r);
1
0
2 sin(mπx) sin(rπx) dx = δ(m, r) (6.6)
> w(y):=1:Int(Y[n](y)*Y[s](y)*w(y),y=0...b)=delta(n,s);
1
0
2 sin(nπy) sin(sπy) dy = δ(n, s) (6.7)
Time-dependent solution
> T[m,n](t):=C(m,n)*exp(−k*lambda[m,n]*t);u[m,n](x,y,t):=T[m,n](t)*X[m](x)*Y[n](y):
T
m,n
(t) := C(m, n)e
−
1
80
(m
2
π
2
+n
2
π
2
)t
(6.8)

The Diffusion Equation in Two Spatial Dimensions 353
Generalized series terms
> u[m,n](x,y,t):=T[m,n](t)*X[m](x)*Y[n](y);
u
m,n
(x,y,t):= 2C(m, n)e
−
1
80
m
2
π
2
+n
2
π
2
t
sin(mπx) sin(nπy) (6.9)
Eigenfunction expansion
> u(x,y,t):=Sum(Sum(u[m,n](x,y,t),m=1..infinity),n=1..infinity);
u(x, y, t) :=
∞
n=1
∞
m=1
2C(m, n)e
−
1
80
m
2
π
2
+n
2
π
2
t
sin(mπx) sin(nπy)
(6.10)
The Fourier coefficients C(m, n) are to be determined from the initial condition function
u(x, y, 0) = f(x, y). We consider the special case where
> f(x,y):=x*(1−x)*y*(1−y);
f(x, y) := x(1 −x)y(1 −y) (6.11)
At time t = 0 we have
> f(x,y)=eval(subs(t=0,u(x,y,t)));
x(1 −x)y(1 −y) =
∞
n=1
∞
m=1
2C(m, n) sin(mπx) sin(nπy)
(6.12)
This is the double Fourier series expansion of f(x, y). From Section 6.5, the Fourier
coefficients C(m, n) were evaluated by taking the double inner product of the initial condition
function f(x, y) with respect to the preceding corresponding orthonormalized eigenfunctions.
This yielded the double integral
> C(m,n):=eval(Int(Int(f(x,y)*X[m](x)*w(x)*Y[n](y)*w(y),x=0..a),y=0..b));C(m,n):=
expand(value(%)):
C(m, n) :=
1
0
1
0
2x(1 −x)y(1 −y) sin(mπx) sin(nπy)dx dy (6.13)
> C(m,n):=factor(subs({sin(m*Pi)=0,cos(m*Pi)=(−1)ˆm,sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},
C(m,n)));
C(m, n) :=
8
−1 +(−1)
n
−1 +(−1)
m
m
3
π
6
n
3
(6.14)
> T[m,n](t):=eval(T[m,n](t));
T
m,n
(t) :=
8
−1 +(−1)
n
−1 +(−1)
m
e
−
1
80
(m
2
π
2
+n
2
π
2
)t
m
3
π
6
n
3
(6.15)
354 Chapter 6
Generalized series terms
> u[m,n](x,y,t):=eval(T[m,n](t)*X[m](x)*Y[n](y));
u
m,n
(x,y,t):=
16
−1 +(−1)
n
−1 +(−1)
m
e
−
1
80
(m
2
π
2
+n
2
π
2
)t
sin(mπx) sin(mπy)
m
3
π
6
n
3
(6.16)
Series solution
> u(x,y,t):=Sum(Sum(u[m,n](x,y,t),m=1..infinity),n=1..infinity);
u(x, y, t) :=
∞
n=1
⎛
⎝
∞
n=1
16
−1 +(−1)
n
−1 +(−1)
m
e
−
1
80
(m
2
π
2
+n
2
π
2
)t
sin(mπx) sin(mπy)
m
3
π
6
n
3
⎞
⎠
(6.17)
First few terms of sum
> u(x,y,t):=sum(sum(u[m,n](x,y,t),m=1..3),n=1..3):
ANIMATION
> animate3d(u(x,y,t),x=0..a,y=0..b,t=0..10,axes=framed,thickness=1);
The preceding animation command illustrates the spatial-time-dependent solution for u(x, y, t).
The animation sequence in Figures 6.2 and 6.3 shows snapshots of the animation at the two
different times t = 0 and t = 2.
ANIMATION SEQUENCE
> u(x,y,0):=subs(t=0,u(x,y,t)):plot3d(u(x,y,0),x=0..a,y=0..b,axes=framed,thickness=1);
0.06
0.05
0.04
0.03
0.02
0.01
0
0
0.2
0.4
0.6
1
1
0.8
0.6
0.4
0.2
0
y
x
0.8
Figure 6.2
> u(x,y,3):=subs(t=3,u(x,y,t)):plot3d(u(x,y,3),x=0..a,y=0..b,axes=framed,thickness=1);

The Diffusion Equation in Two Spatial Dimensions 355
x
y
1
1
0.0012
0.001
0.0008
0.0006
0.0004
0.0002
0
0
0.2
0.4
0.8
0.8
0.6
0.4
0.2
0
0.6
Figure 6.3
EXAMPLE 6.6.2: We seek the temperature distribution in a thin rectangular plate over the
finite two-dimensional domain D ={(x, y) |0 <x<1, 0 <y<1}. The lateral surfaces of the
plate are insulated. The boundaries x = 0 and x = 1 are fixed at temperature 0 and the
boundaries y = 0 and y = 1 are insulated. The initial temperature distribution f(x, y) is given
below and the thermal diffusivity k = 1/50.
SOLUTION: The two-dimensional homogeneous diffusion equation is
∂
∂t
u(x, y, t) = k
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
The boundary conditions are type 1 at x = 0, type 1 at x = 1, type 2 at y = 0, and type 2 at
y = 1:
u(0,y,t)= 0 and u(1,y,t)= 0
and
u
y
(x, 0,t)= 0 and u
y
(x, 1,t)= 0
The initial condition is
u(x, y, 0) = x(1 −x)y
The ordinary differential equations from the method of separation of variables are
d
dt
T(t) +kλT(t) = 0
d
2
dx
2
X(x)+αX(x)= 0
d
2
dy
2
Y(y) +βY(y)= 0
The coupling equation reads
λ = α +β

356 Chapter 6
The boundary conditions on the spatial variables are
X(0) = 0 and X(1) = 0
and
Y
y
(0) = 0 and Y
y
(1) = 0
Assignment of system parameters
> restart:with(plots):a:=1:b:=1:k:=1/50:
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Examples 2.5.1 and 2.5.3.
> alpha[m]:=(m*Pi/a)ˆ2;beta[n]:=(n*Pi/b)ˆ2;lambda[m,n]:=alpha[m]+beta[n];
α
m
:= m
2
π
2
β
n
:= n
2
π
2
λ
m,n
:= m
2
π
2
+n
2
π
2
(6.18)
for m = 1, 2, 3,...,n= 1, 2, 3,...,
> lambda[m,0]:=alpha[m];
λ
m,0
:= m
2
π
2
(6.19)
for n = 0.
Orthonormal eigenfunctions
> X[m](x):=sqrt(2/a)*sin(m*Pi/a*x);X[r](x):=subs(m=r,X[m](x)):
X
m
(x) :=
√
2 sin(mπx) (6.20)
> Y[n](y):=sqrt(2/b)*cos(n*Pi/b*y);Y[s](y):=subs(n=s,Y[n](y)):
Y
n
(y) :=
√
2 cos(nπy) (6.21)
> Y[0](y):=1/sqrt(b);
Y
0
(y) := 1 (6.22)
Statements of orthonormality with their respective weight functions
> w(x):=1:Int(X[m](x)*X[r](x)*w(x),x=0...a)=delta(m,r);
1
0
2 sin(mπx) sin(rπx)dx = δ(m, r) (6.23)
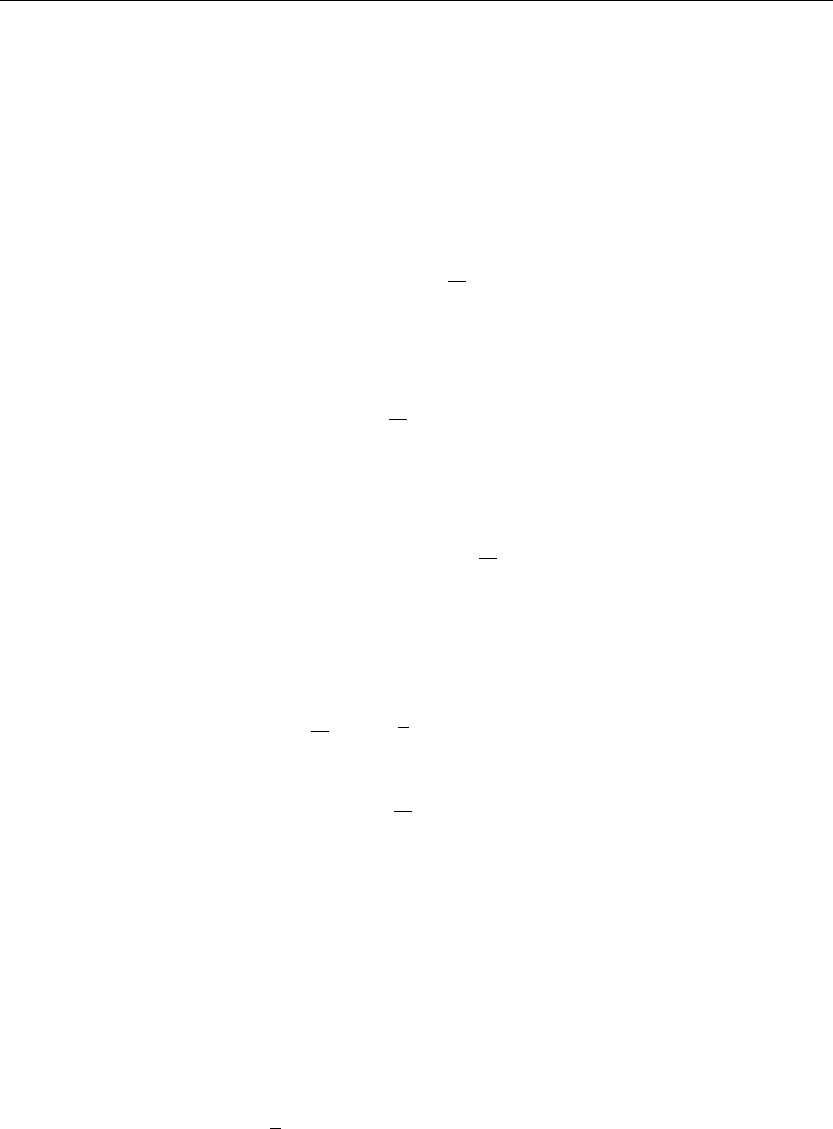
The Diffusion Equation in Two Spatial Dimensions 357
> w(y):=1:Int(Y[n](y)*Y[s](y)*w(y),y=0...b)=delta(n,s);
1
0
2 cos(nπy) cos(sπy)dy = δ(n, s) (6.24)
Time-dependent solution
For n = 1, 2, 3,...,m= 1, 2, 3,...,
> T[m,n](t):=C(m,n)*exp(−k*lambda[m,n]*t);
T
m,n
(t) := C(m, n)e
−
1
50
(m
2
π
2
+n
2
π
2
)t
(6.25)
Generalized series terms
> u[m,n](x,y,t):=T[m,n](t)*X[m](x)*Y[n](y);
u
m,n
(x,y,t):= 2C(m, n)e
−
1
50
(m
2
π
2
+n
2
π
2
)t
sin(mπx) cos(nπy) (6.26)
For n = 0,m= 1, 2, 3,...,
> T[m,0](t):=C(m,0)*exp(−k*lambda[m,0]*t);u[m,0](x,y,t):=T[m,0](t)*X[m](x)*Y[0](y):
T
m,0
(t) := C(m, 0)e
−
1
50
m
2
π
2
t
(6.27)
Eigenfunction expansion
> u(x,y,t):=Sum(u[m,0](x,y,t),m=1..infinity)+Sum(Sum(u[m,n](x,y,t),m=1..infinity),n=
1..infinity);
u(x, y, t) :=
∞
m=1
C(m, 0)e
−
1
50
m
2
π
2
t
√
2 sin(mπx)
+
∞
n=1
∞
m=1
2C(m, n)e
−
1
50
(m
2
π
2
+n
2
π
2
)t
sin(mπx) cos(nπy)
(6.28)
The Fourier coefficients C(m, n) are to be determined from the initial condition function
u(x, y, 0) = f(x, y). We consider the special case where
> f(x,y):=x*(1−x)*y;
f(x, y) := x(1 −x)y (6.29)
At time t = 0 we have
> f(x,y)=eval(subs(t=0,u(x,y,t)));
x(1 −x)y =
∞
m=1
C(m, 0)
√
2 sin(mπx) +
∞
n=1
∞
m=1
2C(m, n) sin(mπx) cos(nπy)
(6.30)
