Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.

This page intentionally left blank

CHAPTER 7
The Wave Equation in Two
Spatial Dimensions
7.1 Introduction
In Chapter 4, we examined the wave partial differential equation in only one spatial dimension.
Here, we examine the wave equation in two spatial dimensions. Thus, we will be considering
problems with a total of three independent variables: the two spatial variables and time. The
method of separation of variables will be used, and we will see the development of two
independent Sturm-Liouville problems—one for each of the two spatial variables. The final
solutions will have the form of a double Fourier series. We will consider problems in both the
rectangular and cylindrical coordinate systems.
7.2 Two-Dimensional Wave Operator in Rectangular
Coordinates
In the one-dimensional wave equation, as discussed in Chapter 4, the second-order partial
derivative with respect to the spatial variable x can be viewed as the first term of the Laplacian
operator. Thus, an extension of this Laplacian operator to higher dimensions is natural, and we
show that wave phenomena in two dimensions can be described by the following
nonhomogeneous partial differential equation in the rectangular coordinate system:
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
−γ
∂
∂t
u(x, y, t)
+h(x, y, t)
In the preceding equation, for the situation of wave phenomena, u(x, y, t) denotes the
spatial-time-dependent wave amplitude, c denotes the wave speed, γ denotes the damping
coefficient of the medium, and h(x, y, t) denotes the presence of any external applied forces
acting on the system. We have assumed the medium to be isotropic and uniform, so the
preceding coefficients are spatially invariant and we write them as constants.
Because we will be considering only example problems that have no extension along the
z-axis, we write the Laplacian operator with no z-dependent terms.
© 2009, 2003, 1999 Elsevier Inc. 409

410 Chapter 7
The given partial differential equation for wave phenomena is characterized by the fact that it
relates the second partial derivative with respect to the time variable with the second partial
derivatives with respect to the spatial variables.
We can write this nonhomogeneous equation in terms of the linear wave operator as
L(u) = h(x, y, t)
where the wave operator in rectangular coordinates in two spatial dimensions reads
L(u) =
∂
2
∂t
2
u(x, y, t) −c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
+γ
∂
∂t
u(x, y, t)
If h(x, y, t) = 0, then there are no external applied forces acting on the system and the
preceding nonhomogeneous partial differential equation reduces to its corresponding
homogeneous equation
L(u) = 0
A typical illustrative problem for a homogeneous wave equation in two spatial dimensions
reads as follows. We consider the transverse vibrations in a thin rectangular membrane over the
finite two-dimensional rectangular domain D ={(x, y) |0 <x<π,0 <y<π}. The membrane
is in a medium with a small damping coefficient γ. The boundaries are held fixed, and the
membrane has an initial displacement function f(x, y) and an initial speed function g(x, y)
given as follows. There are no external forces acting on the system, and the wave speed is c.
We seek the transverse wave amplitude u(x, y, t).
The homogeneous wave equation for this problem is
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
−γ
∂
∂t
u(x, y, t)
Since the boundaries of the membrane are held fixed, the boundary conditions on the problem
are type 1 at x = 0 and x = π and type 1 at y = 0 and y = π.
u(0,y,t)= 0 and u(π,y,t)= 0
and
u(x, 0,t)= 0 and u(x, π, t) = 0
The initial displacement function is
u(x, y, 0) = f(x, y)
and the initial speed function is
u
t
(x, y, 0) = g(x, y)

The Wave Equation in Two Spatial Dimensions 411
We now examine the solution to this homogeneous partial differential equation over a finite
two-dimensional domain with homogeneous boundary conditions using the method of
separation of variables.
7.3 Method of Separation of Variables for the
Wave Equation
The homogeneous wave equation for a uniform system in two dimensions in rectangular
coordinates can be written
∂
2
∂t
2
u(x, y, t) −c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
+γ
∂
∂t
u(x, y, t)
= 0
This can be rewritten in the more familiar form
∂
2
∂t
2
u(x, y, t) +γ
∂
∂t
u(x, y, t)
= c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
Generally, one seeks a solution to this problem over the finite two-dimensional domain
D ={(x, y) |0 <x<a,0 <y<b} subject to the regular homogeneous boundary conditions
κ
1
u(0,y,t)+κ
2
u
x
(0,y,t)= 0
κ
3
u(a, y, t) +κ
4
u
x
(a,y,t)= 0
κ
5
u(x, 0,t)+κ
6
u
y
(x, 0,t)= 0
κ
7
u(x, b, t) +κ
8
u
y
(x,b,t)= 0
along with the two initial conditions
u(x, y, 0) = f(x, y) and u
t
(x, y, 0) = g(x, y)
In the method of separation of variables, as in Chapter 4, the character of the equation is such
that we can assume a solution in the form of a product
u(x, y, t) = X(x)Y(y)T(t)
Because the three independent variables in the partial differential equation are the spatial
variables x and y, and the time variable t, this assumed solution is written as a product of three
functions; one is an exclusive function of x, one is an exclusive function of y, and the last is an
exclusive function of t.
Substituting this assumed solution into the partial differential equation, we get
X(x)Y(y)
d
2
dt
2
T(t)
+γX(x)Y(y)
d
dt
T(t)
=c
2
d
2
dx
2
X(x)
Y(y)T(t) +X(x)
d
2
dy
2
Y(y)
T(t)

412 Chapter 7
Dividing both sides by the product solution yields
d
2
dt
2
T(t) +γ
d
dt
T(t)
c
2
T(t)
=
d
2
dx
2
X(x)
Y(y) +X(x)
d
2
dy
2
Y(y)
X(x)Y(y)
Because the left-hand side of the preceding is an exclusive function of t and the right-hand side
an exclusive function of both x and y, and x, y, and t are independent, then the only way this
can hold for all values of t, x, and y is to set each side equal to a constant. Doing so, we get the
following three ordinary differential equations in terms of the separation constants λ, α, and β:
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t)= 0
d
2
dx
2
X(x)+αX(x)= 0
d
2
dy
2
Y(y) +βY(y)= 0
along with the coupling equation
λ = α +β
The preceding differential equation in t is an ordinary second-order linear homogeneous
differential equation for which we already have the solution from Section 1.4. The second and
third differential equations in x and y are ordinary second-order linear, homogeneous
differential equations of the Euler type for which we already have the solutions from
Section 1.4. We easily recognize each of the two spatial differential equations as being
Sturm-Liouville types.
7.4 Sturm-Liouville Problem for the Wave Equation in
Two Dimensions
The second and third differential equations in Section 7.3, in the spatial variables x and y, must
each be solved subject to their respective homogeneous spatial boundary conditions.
We first consider the x-dependent differential equation over the finite interval
I ={x |0 <x<a}. The Sturm-Liouville problem for the x-dependent portion of the wave
equation consists of the ordinary differential equation
d
2
dx
2
X(x)+αX(x)= 0
along with its respective corresponding regular homogeneous boundary conditions
κ
1
X(0) +κ
2
X
x
(0) = 0

The Wave Equation in Two Spatial Dimensions 413
and
κ
3
X(a)+κ
4
X
x
(a) = 0
We recognize the preceding problem in the spatial variable x to be a regular Sturm-Liouville
eigenvalue problem where the allowed values of α are called the system “eigenvalues” and the
corresponding solutions are called the “eigenfunctions.” Note that the ordinary differential
equation given here is of the Euler type, and the weight function is w(x) = 1. The indexed
eigenvalues and corresponding eigenfunctions are given, respectively, as
α
m
,X
m
(x)
for m = 0, 1, 2, 3, ....
These eigenfunctions can be normalized, with respect to the weight function w(x) = 1, and the
corresponding statement of orthonormality reads
a
0
X
m
(x)X
r
(x)dx = δ(m, r)
Similarly, we now focus on the third differential equation in the spatial variable y subject to the
homogeneous spatial boundary conditions over the finite interval I ={y |0 <y<b}. The
Sturm-Liouville problem for the y-dependent portion of the wave equation consists of the
ordinary differential equation
d
2
dy
2
Y(y) +βY(y)= 0
along with its respective corresponding regular homogeneous boundary conditions
κ
5
Y(0) +κ
6
Y
y
(0) = 0
and
κ
7
Y(b) +κ
8
Y
y
(b) = 0
We recognize this problem in the spatial variable y as a regular Sturm-Liouville eigenvalue
problem where the allowed values of β are called the system “eigenvalues” and the
corresponding solutions are called the “eigenfunctions.” Note that the ordinary differential
equation given here is of the Euler type, and the weight function is w(y) = 1. The indexed
eigenvalues and corresponding eigenfunctions are given, respectively, as
β
n
,Y
n
(y)
for n = 0, 1, 2, 3, ....
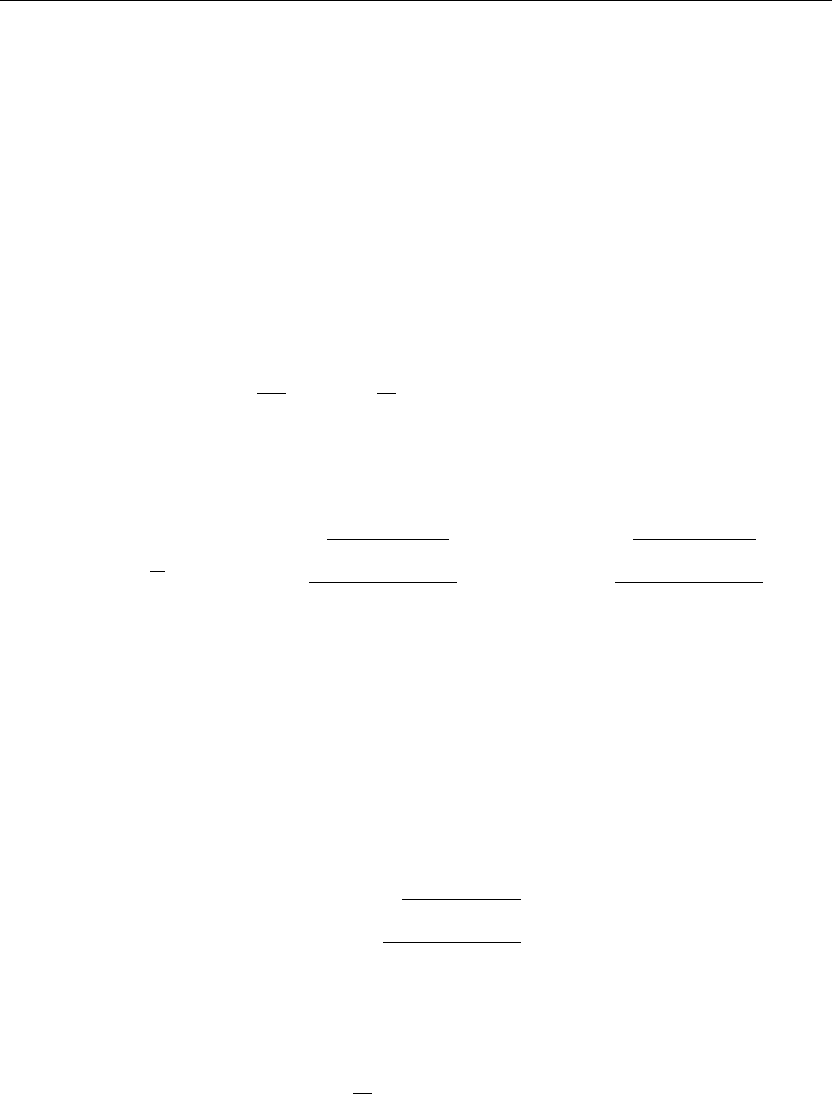
414 Chapter 7
These eigenfunctions can be normalized, with respect to the weight function w(y) = 1, and the
corresponding statement of orthonormality reads
b
0
Y
n
(y)Y
s
(y)dy = δ(n, s)
What was stated in Section 2.2 about regular Sturm-Liouville eigenvalue problems in one
dimension can be extended to two dimensions here; that is, the products of the two spatial
eigenfunctions form a “complete” set with respect to any piecewise smooth function f(x, y)
over the finite two-dimensional domain D ={(x, y) |0 <x<a,0 <y<b}.
Finally, the time-dependent differential equation reads
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t)= 0
From Section 1.4 on second-order linear differential equations, if we assume the damping
coefficient to be small, then the solution to the preceding, in terms of the allowed eigenvalues
λ
m, n
,is
T
m, n
(t) = e
−
γt
2
⎛
⎜
⎝
A(m, n) cos
⎛
⎜
⎝
4λ
m, n
c
2
−γ
2
t
2
⎞
⎟
⎠
+B(m, n) sin
⎛
⎜
⎝
4 λ
m, n
c
2
−γ
2
t
2
⎞
⎟
⎠
⎞
⎟
⎠
where the coupling equation now reads
λ
m, n
= α
m
+β
n
The coefficients A(m, n) and B(m, n) are unknown arbitrary constants. Throughout most of our
example problems, we make the assumption of small damping in the system—that is,
γ
2
< 4 λ
m, n
c
2
and the (m, n)th-mode angular frequency is
ω
m, n
=
4λ
m, n
c
2
−γ
2
2
Thus, by the method of separation of variables, we arrive at an infinite number of indexed
product solutions for the homogeneous wave partial differential equation, over a finite domain,
given as
u
m,n
(x,y,t)= X
m
(x)Y
n
(y)e
−
γt
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
for m = 0, 1, 2, 3, ..., and n = 0, 1, 2, 3, ....

The Wave Equation in Two Spatial Dimensions 415
Since the partial differential operator is linear, any superposition of solutions to the
homogeneous equation is also a solution to the problem. Thus, we can write the general
solution to the homogeneous partial differential equation as the double-infinite sum
u(x, y, t) =
∞
n=0
∞
m=0
X
m
(x)Y
n
(y)e
−
γt
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
This equation is the double Fourier series eigenfunction expansion form of the solution to the
wave partial differential equation. The terms of this sum form the “basis vectors” of the
solution space of the partial differential equation. Similar to a partial differential equation in
only one dimension, there are an infinite number of basis vectors in the solution space, and we
say the dimension of the solution space is infinite. We demonstrate the preceding concepts with
the solution of an illustrative problem.
DEMONSTRATION: We consider the transverse vibrations in a thin rectangular membrane
over the finite two-dimensional domain D ={(x, y) |0 <x<π,0 <y<π}. The membrane is
in a medium with small damping γ. The boundaries are held fixed, and the membrane has an
initial displacement function f(x, y) and an initial speed function g(x, y) given as follows.
There are no external forces acting on the system, and the wave speed is c. We seek the
transverse wave amplitude u(x, y, t).
SOLUTION: The homogeneous wave equation for this problem is
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
−γ
∂
∂t
u(x, y, t)
The given boundary conditions on the problem are type 1 at x = 0 and x = π and type 1 at
y = 0 and y = π.
u(0,y,t)= 0 and u(π,y,t)= 0
and
u(x, 0,t)= 0 and u(x, π, t) = 0
The initial displacement function is
u(x, y, 0) = f(x, y)
and the initial speed function is
u
t
(x, y, 0) = g(x, y)

416 Chapter 7
From the method of separation of variables, we obtain the three ordinary differential
equations
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t)= 0
d
2
dx
2
X(x)+αX(x)= 0
d
2
dy
2
Y(y) +βY(y)= 0
along with the coupling equation
λ = α +β
We first consider the solution of the x equation. The differential equation is of the Euler type
with weight function w(x) = 1, and the corresponding boundary conditions on the x-dependent
equation are both type 1:
X(0) = 0 and X(π) = 0
From the similar problem in Example 2.5.1, the allowed eigenvalues and corresponding
orthonormal eigenfunctions are
α
m
= m
2
and
X
m
(x) =
2
π
sin(mx)
for m = 1, 2, 3, ....
Similarly, for the y equation, the differential equation is of the Euler type with weight function
w(y) = 1 and the corresponding boundary conditions are, again, both of type 1:
Y(0) = 0 and Y(π) = 0
The allowed eigenvalues and corresponding orthonormal eigenfunctions from Example 2.5.1
are
β
n
= n
2
and
Y
n
(y) =
2
π
sin(ny)
for n = 1, 2, 3, ....
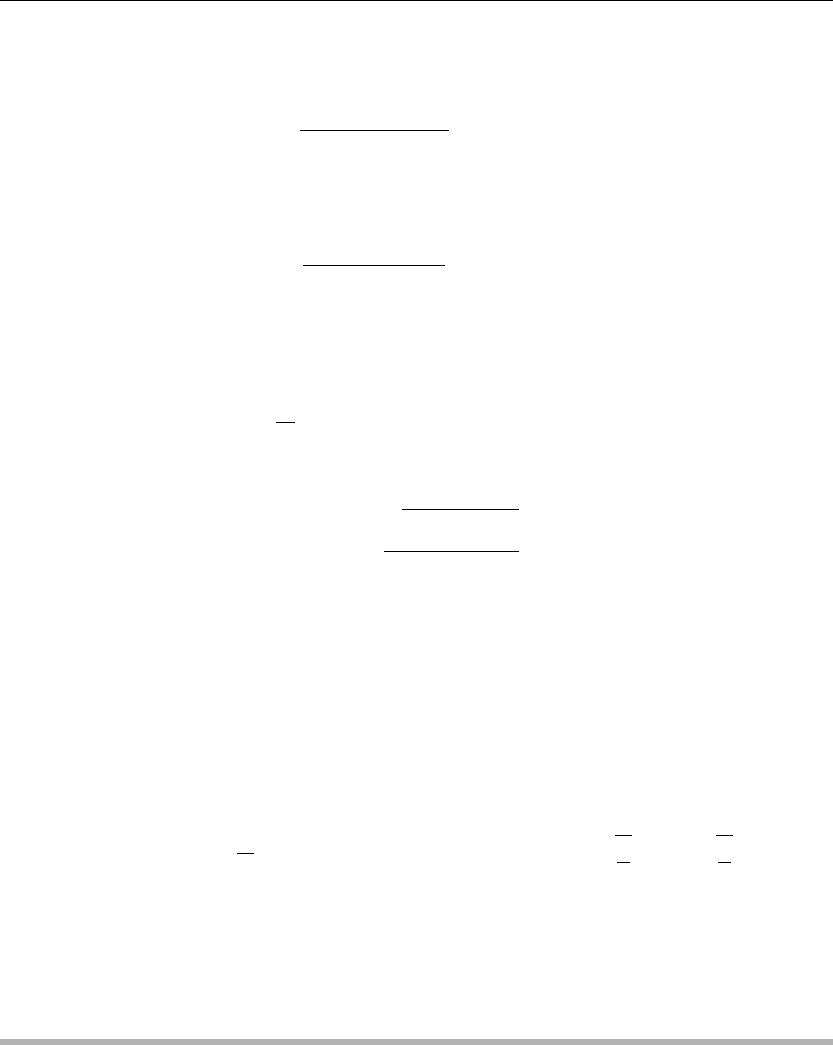
The Wave Equation in Two Spatial Dimensions 417
The corresponding statements of orthonormality for each of the preceding eigenfunctions, with
their respective weight functions, read
π
0
2 sin(mx) sin(rx)
π
dx = δ(m, r)
and
π
0
2 sin(ny) sin(sy)
π
dy = δ(n, s)
for m, r = 1, 2, 3,..., and n, s = 1, 2, 3,....
Finally, the time-dependent differential equation has the solution
T
m, n
(t) = e
−
γt
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
where the damped angular frequency ω
m, n
is given as
ω
m, n
=
4λ
m, n
c
2
−γ
2
2
and the coupling equation is
λ
m, n
= m
2
+n
2
for m = 1, 2, 3,..., and n = 1, 2, 3,.... The terms A(m, n) and B(m, n) are unknown arbitrary
constants.
The final eigenfunction expansion form of the solution is constructed from the superposition of
the products of the time-dependent solution and the preceding x- and y-dependent
eigenfunction. The solution reads
u(x, y, t) =
∞
n=1
∞
m=1
2 e
−
γt
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
1
π
sin(mx)
1
π
sin(ny)
The coefficients A(m, n) and B(m, n) are to be determined from the initial conditions.
7.5 Initial Conditions for the Wave Equation in Rectangular
Coordinates
We now consider the initial conditions on the problem. At time t = 0, we have two conditions.
The first condition is the initial displacement function given as
u(x, y, 0) = f(x, y)
