Articolo G.A. Partial Differential Equations and Boundary Value Problems with Maple V
Подождите немного. Документ загружается.


418 Chapter 7
and the second condition is the initial speed function given as
u
t
(x, y, 0) = g(x, y)
Substitution of the first condition into the following general solution
u(x, y, t) =
∞
n=0
∞
m=0
X
m
(x)Y
n
(y)e
−
γt
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
at time t = 0 yields
f(x, y) =
∞
n=0
∞
m=0
X
m
(x)Y
n
(y)A(m, n)
Forcing the second condition into the time derivative of the solution at time t = 0 yields
g(x, y) =
∞
n=0
∞
m=0
B(m, n)ω
m, n
−
A(m, n)γ
2
X
m
(x)Y
n
(y)
Because the eigenfunctions of the regular Sturm-Liouville problem form a complete set with
respect to piecewise smooth functions over the finite two-dimensional domain, then the
preceding sums are the generalized double Fourier series expansions of the functions f(x, y)
and g(x, y), respectively, in terms of the allowed eigenfunctions. We can evaluate the unknown
Fourier coefficients A(m, n) and B(m, n) by taking advantage of the familiar orthonormality
statements.
Using the procedure in Section 2.4, for the generalized Fourier series expansion in one
variable, we evaluate the double Fourier coefficients A(m, n) and B(m, n) as follows. We take
the double inner products of both sides of the preceding equations with respect to the x- and
y-dependent eigenfunctions. Assuming the validity of the interchange between the integration
and summation operations, we get for the first condition
b
0
a
0
f(x, y)X
r
(x)Y
s
(y)dx dy =
∞
n=0
⎛
⎝
∞
m=0
A(m, n)
⎛
⎝
a
0
X
m
(x)X
r
(x)dx
⎞
⎠
⎛
⎝
b
0
Y
n
(y)Y
s
(y)dy
⎞
⎠
⎞
⎠
Taking advantage of the statements of orthonormality from Section 7.4 for the two integrals on
the right yields
b
0
a
0
f(x, y)X
r
(x)Y
s
(y)dx dy =
∞
n=0
∞
m=0
A(m, n)δ(m, r)δ(n, s)

The Wave Equation in Two Spatial Dimensions 419
Due to the mathematical nature of the Kronecker delta functions in this sum, only the m = r,
n = s term survives, and the double Fourier coefficient A(m, n) evaluates to
A(m, n) =
b
0
a
0
f(x, y)X
m
(x)Y
n
(y)dx dy
Similarly, for the second condition, we have
b
0
a
0
g(x, y)X
r
(x)Y
s
(y)dx dy =
∞
n=0
⎛
⎝
∞
m=0
B(m, n)ω
m, n
−
A(m, n)γ
2
⎛
⎝
a
0
X
m
(x)X
r
(x)dx
⎞
⎠
⎛
⎝
b
0
Y
n
(y)Y
s
(y)dy
⎞
⎠
⎞
⎠
Again, taking advantage of the statements of orthonormality from Section 7.4 for the two
integrals on the right yields
b
0
a
0
g(x, y)X
r
(x)Y
s
(y)dx dy =
∞
n=0
∞
m=0
B(m, n)ω
m, n
−
A(m, n)γ
2
δ(m, r)δ(n, s)
Again, due to the mathematical nature of the Kronecker delta functions in this sum, only the
m = r, n = s term survives the sum, and, combining the previous value for A(m, n), the double
Fourier coefficient B(m, n) evaluates to
B(m, n) =
b
0
a
0
f(x,y)γ
2
+g(x, y)
X
m
(x)Y
n
(y)
ω
m, n
dx dy
We now demonstrate the evaluation of the Fourier coefficients A(m, n) and B(m, n) for the
example problem in Section 7.4.
DEMONSTRATION: We consider the special case where there is no damping in the system
(γ = 0), the wave speed c = 1, the initial displacement function is u(x, y, 0) = f(x, y) where
f(x, y) = xy(π −x)(π −y)
and the initial speed function is u
t
(x, y, 0) = g(x, y) where
g(x, y) = 0
SOLUTION: Evaluating the wave angular frequency for c = 1 and γ = 0, we get
ω
m, n
=
m
2
+n
2

420 Chapter 7
The Fourier coefficient A(m, n) for the given f(x, y) yields the integral
A(m, n) =
π
0
π
0
x(π −x)y(π −y)X
m
(x)Y
n
(y)dx dy
where, from the preceding example, the orthonormal eigenfunctions are
X
m
(x) =
2
π
sin(mx)
and
Y
n
(y) =
2
π
sin(ny)
for m = 1, 2, 3,..., and n = 1, 2, 3,.... Insertion of these eigenfunctions into this integral
yields
A(m, n) =
π
0
π
0
2x(π −x)y(π −y) sin(mx) sin(ny)
π
dx dy
which evaluates to
A(m, n) =
8
(−1)
m
−1
(−1)
n
−1
n
3
m
3
π
Similarly, for γ = 0 and g(x, y) = 0, the integral for B(m, n) evaluates to
B(m, n) = 0
Thus, with knowledge of the coefficients A(m, n) and B(m, n), the final series form of the
eigenfunction expansion solution to the problem, from Section 7.4, reads
u(x, y, t) =
∞
n=1
⎛
⎝
∞
m=1
16
(−1)
m
−1
(−1)
n
−1
cos
m
2
+n
2
t
sin(mx) sin(ny)
n
3
m
3
π
2
⎞
⎠
The details for the development of this solution and the graphics are given later in one of the
Maple worksheet examples following.
7.6 Example Wave Equation Problems in Rectangular
Coordinates
We now consider several examples of partial differential equations for wave phenomena under
various homogeneous boundary conditions over finite two-dimensional domains in the
rectangular coordinate system. We note that all the spatial ordinary differential equations are
of the Euler type with weight functions equal to 1.
The Wave Equation in Two Spatial Dimensions 421
EXAMPLE 7.6.1: We seek the wave amplitude u(x, y, t) for the transverse vibrations on a thin
rectangular membrane over the finite two-dimensional domain D ={(x, y) |0 <x<π,
0 <y<π}. The membrane is in a medium with no damping and the wave speed is c = 1. The
boundaries are held fixed, and the membrane has an initial displacement distribution f(x, y)
and an initial speed distribution g(x, y) given as follows.
SOLUTION: The two-dimensional homogeneous wave equation is
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
−γ
∂
∂t
u(x, y, t)
The boundary conditions are type 1 at x = 0, type 1 at x = π,type1aty = 0, and type 1 at
y = π:
u(0,y,t)= 0 and u(π,y,t)= 0
and
u(x, 0,t)= 0 and u(x, π, t) = 0
The initial conditions are
u(x, y, 0) = x(π −x)y(π −y) and u
t
(x, y, 0) = 0
The ordinary differential equations from the method of separation of variables are
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t)= 0
d
2
dx
2
X(x)+αX(x)= 0
d
2
dy
2
Y(y) +βY(y)= 0
The coupling equation reads
λ = α +β
The boundary conditions on the spatial equations are
X(0) = 0 and X(π) = 0
and
Y(0) = 0 and Y(π) = 0
Assignment of system parameters
> restart:with(plots):a:=Pi:b:=Pi:c:=1:unprotect(gamma):gamma:=0:

422 Chapter 7
Allowed eigenvalues and corresponding orthonormal eigenfunctions are obtained from
Example 2.5.1.
> alpha[m]:=(m*Pi/a)ˆ2;beta[n]:=(n*Pi/b)ˆ2;lambda[m,n]:=alpha[m]+beta[n];
α
m
:=m
2
β
n
:=n
2
λ
m, n
:=m
2
+n
2
(7.1)
for m = 1, 2, 3,..., and n = 1, 2, 3,....
> X[m](x):=sqrt(2/a)*sin(m*Pi/a*x);X[r](x):=subs(m=r,X[m](x)):
X
m
(x) :=
√
2 sin(mx)
√
π
(7.2)
> Y[n](y):=sqrt(2/b)*sin(n*Pi/b*y);Y[s](y):=subs(n=s,Y[n](y)):
Y
n
(y) :=
√
2 sin(ny)
√
π
(7.3)
Statements of orthonormality with their respective weight functions
> w(x):=1:Int(X[m](x)*X[r](x)*w(x),x=0..a)=delta(m,r);
π
0
2 sin(mx) sin(rx)
π
dx = δ(m, r) (7.4)
> w(y):=1:Int(Y[n](y)*Y[s](y)*w(y),y=0..b)=delta(n,s);
π
0
2 sin(ny) sin(sy)
π
dy = δ(n, s) (7.5)
Time-dependent solution
> T[m,n](t):=exp(−gamma/2*t)*(A(m,n)*cos(omega[m,n]*t)+B(m,n)*sin(omega[m,n]*t));
T
m, n
(t) := A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
(7.6)
Generalized series terms
> u[m,n](x,y,t):=T[m,n](t)*X[m](x)*Y[n](y);
u
m, n
(x,y,t):=
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m,n
t
sin(mx) sin(ny)
π
(7.7)

The Wave Equation in Two Spatial Dimensions 423
Eigenfunction expansion
> u(x,y,t):=Sum(Sum(u[m,n](x,y,t),m=1..infinity),n=1..infinity);
u(x, y, t) :=
∞
n=1
∞
m=1
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
sin(mx) sin(ny)
π
(7.8)
> omega[m,n]:=sqrt(4*lambda[m,n]*cˆ2−gammaˆ2)/2;
ω
m, n
:=
m
2
+n
2
(7.9)
We consider the special case where the initial condition functions u(x, y, 0) = f(x, y) and
u
t
(x, y, 0) = g(x, y) are given as
> f(x,y):=x*(Pi−x)*y*(Pi−y);
f(x, y) := x(π −x)y(π −y) (7.10)
> g(x,y):=0;
g(x, y) := 0 (7.11)
From Section 7.5, the double Fourier coefficients A(m, n) and B(m, n) are determined from the
integrals
> A(m,n):=eval(Int(Int(f(x,y)*X[m](x)*w(x)*Y[n](y)*w(y),x=0..a),y=0..b));A(m,n):
=expand(value(%)):
A(m, n) :=
π
0
π
0
2x(π −x)y(π −y) sin(mx) sin(ny)
π
dx dy (7.12)
> A(m,n):=factor(subs({sin(m*Pi)=0,cos(m*Pi)=(−1)ˆm,sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},
A(m,n)));
A(m, n) :=
8
−1 +(−1)
n
−1 +(−1)
m
πm
3
n
3
(7.13)
> B(m,n):=eval(Int(Int((f(x,y)*gamma/2+g(x,y))/(omega[m,n])*X[m](x)*Y[n](y),x=0..a),
y=0..b));B(m,n):=expand(value(%)):
B(m, n) :=
π
0
π
0
0dx dy (7.14)
> B(m,n):=factor(subs({sin(m*Pi)=0,cos(m*Pi)=(−1)ˆm,sin(n*Pi)=0,cos(n*Pi)=(−1)ˆn},
B(m,n)));
B(m, n) := 0 (7.15)
424 Chapter 7
> T[m,n](t):=eval(T[m,n](t));
T
m, n
(t) :=
8
−1 +(−1)
n
−1 +(−1)
m
cos
m
2
+n
2
t
πm
3
n
3
(7.16)
Generalized series terms
> u[m,n](x,y,t):=eval(T[m,n](t)*X[m](x)*Y[n](y));
u
m, n
(x,y,t):=
16(−1 +(−1)
n
)
−1 +(−1)
m
cos
m
2
+n
2
t
sin(mx) sin(ny)
π
2
m
3
n
3
(7.17)
Series solution
> u(x,y,t):=Sum(Sum(u[m,n](x,y,t),m=1..infinity),n=1..infinity);
u(x, y, t) :=
∞
n=1
⎛
⎝
∞
m=1
16
−1 +(−1)
n
−1 +(−1)
m
cos
m
2
+n
2
t
sin(mx) sin(ny)
π
2
m
3
n
3
⎞
⎠
(7.18)
First few terms of sum
> u(x,y,t):=sum(sum(u[m,n](x,y,t),m=1..1),n=1..1):
ANIMATION
> animate3d(u(x,y,t),x=0..a,y=0..b,t=0..3,axes=framed,thickness=1);
The preceding animation command illustrates the spatial-time-dependent solution for u(x, y, t).
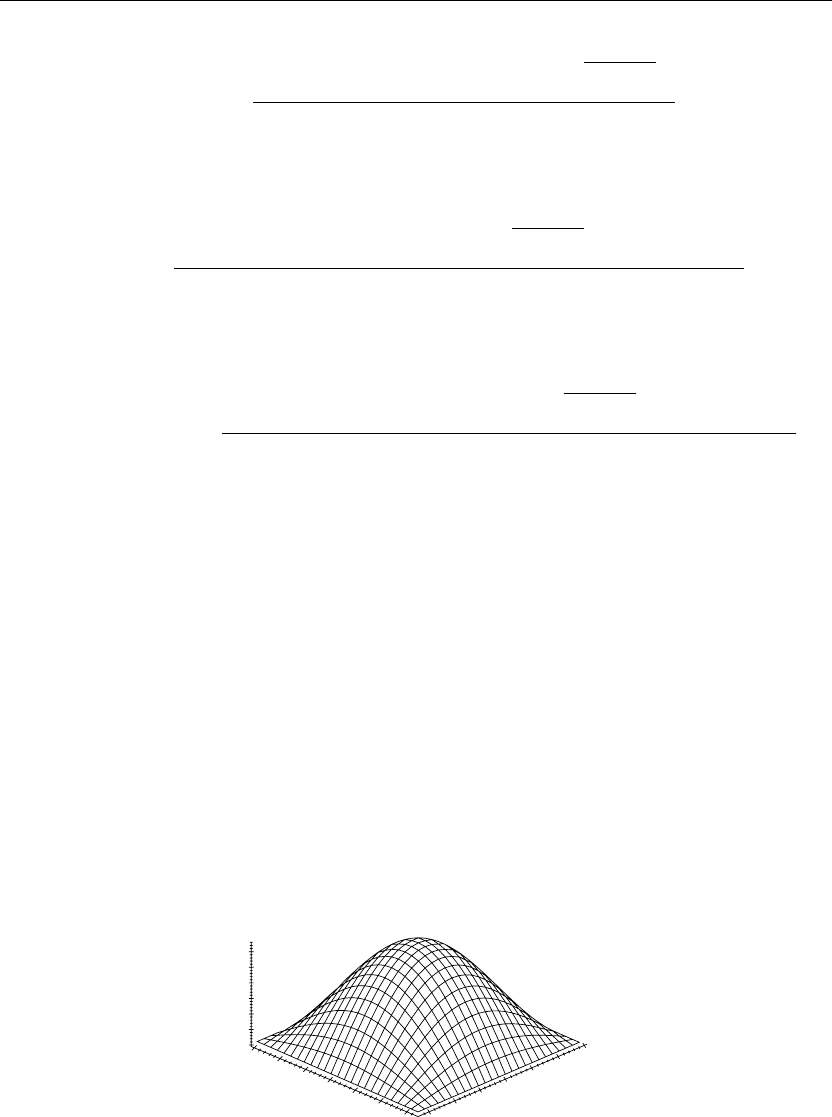
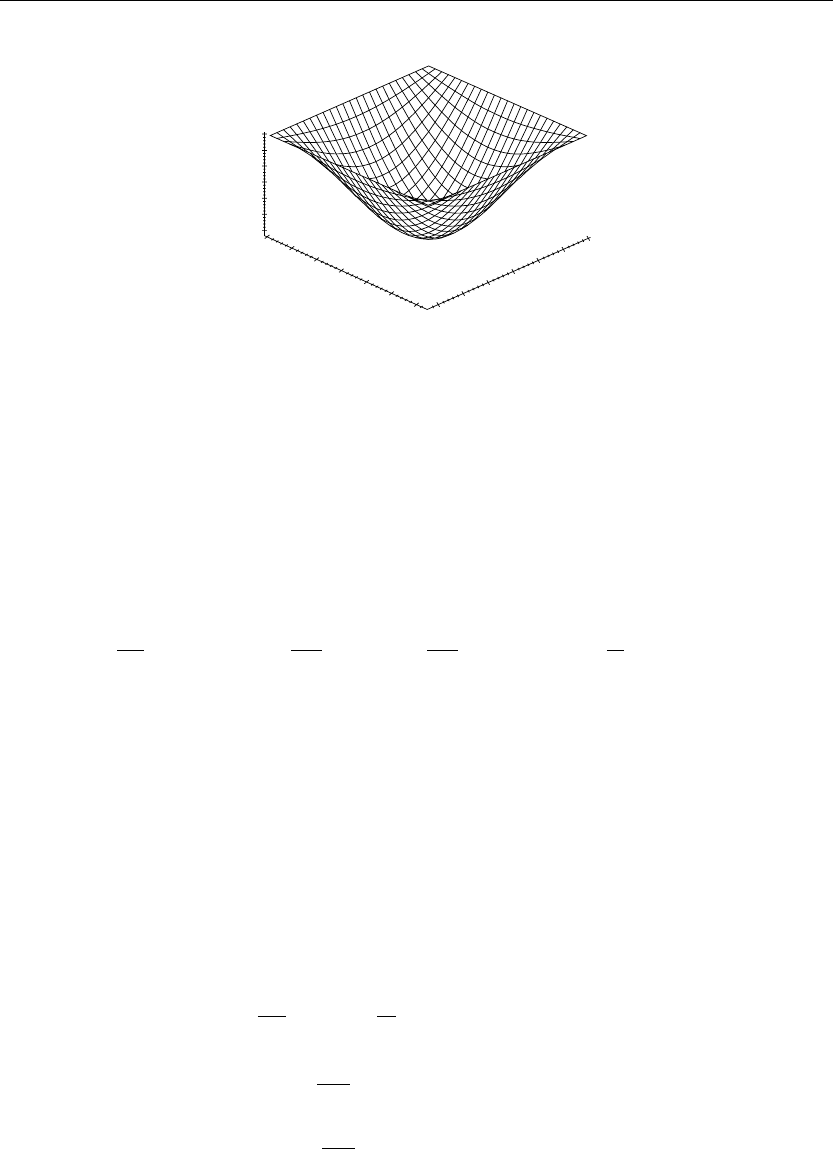
The animation sequence in Figures 7.1 and 7.2 shows snapshots of the animation at times t = 0
and t = 2.
ANIMATION SEQUENCE
> u(x,y,0):=subs(t=0,u(x,y,t)):plot3d(u(x,y,0),x=0..a,y=0..b,axes=framed,thickness=1);
6
5
4
3
2
1
0
y
x
0.5
1
1.5
2
2.5
3
2.5
1.5
0.5
2
1
3
0
0
Figure 7.1
The Wave Equation in Two Spatial Dimensions 425
> u(x,y,2):=subs(t=2,u(x,y,t)):plot3d(u(x,y,2),x=0..a,y=0..b,axes=framed,thickness=1);
0
21
22
23
24
25
26
0
1
2
3
3
2
1
x
0.5
0.5
1.5
y
2.5
2.5
1.5
0
Figure 7.2
EXAMPLE 7.6.2: We seek the wave amplitude u(x, y, t) for the transverse wave propagation
on a thin rectangular membrane over the finite two-dimensional domain D ={(x, y) |0 <x<π,
0 <y<π}. The membrane is in a medium with zero damping, and the wave speed is c = 1/2.
The boundaries x = 0 and x = π are unsecured and the boundaries y = 0 and y = π are held
fixed. The initial displacement distribution f(x, y) and the initial speed distribution g(x, y) are
given as follows.
SOLUTION: The two-dimensional homogeneous wave equation is
∂
2
∂t
2
u(x, y, t) = c
2
∂
2
∂x
2
u(x, y, t) +
∂
2
∂y
2
u(x, y, t)
−γ
∂
∂t
u(x, y, t)
The boundary conditions are type 2 at x = 0, type 2 at x = π,type1aty = 0, and type 1 at
y = π:
u
x
(0,y,t)= 0 and u
x
(π,y,t)= 0
and
u(x, 0,t)= 0 and u(x, π, t) = 0
The initial conditions are
u(x, y, 0) = xy(π −y) and u
t
(x, y, 0) = 0
The ordinary differential equations from the method of separation of variables are
d
2
dt
2
T(t) +γ
d
dt
T(t)
+c
2
λT(t)= 0
d
2
dx
2
X(x)+αX(x)= 0
d
2
dy
2
Y(y) +βY(y)= 0

426 Chapter 7
The coupling equation reads
λ = α +β
The boundary conditions on the spatial equations are
X
x
(0) = 0 and X
x
(π) = 0
and
Y(0) = 0 and Y(π) = 0
Assignment of system parameters
> restart:with(plots):a:=Pi:b:=Pi:c:=1/2:unprotect(gamma):gamma:=0:
Allowed eigenvalues and orthonormal eigenfunctions are obtained from Examples 2.5.1
and 2.5.3.
> alpha[m]:=(m*Pi/a)ˆ2;beta[n]:=(n*Pi/b)ˆ2;lambda[m,n]:=alpha[m]+beta[n];lambda[0,n]
:=beta[n];
α
m
:=m
2
β
n
:=n
2
λ
m, n
:=m
2
+n
2
λ
0,n
:=n
2
(7.19)
for m = 0, 1, 2, 3,..., and n = 1, 2, 3,....
Orthonormal eigenfunctions
For m = 0,
> X[0](x):=1/sqrt(a);
X
0
(x) :=
1
√
π
(7.20)
For m = 1, 2, 3,...,
> X[m](x):=sqrt(2/a)*cos(m*Pi/a*x);X[r](x):=subs(m=r,X[m](x)):
X
m
(x) :=
√
2 cos(mx)
√
π
(7.21)
For n = 1, 2, 3,...,

The Wave Equation in Two Spatial Dimensions 427
> Y[n](y):=sqrt(2/b)*sin(n*Pi/b*y);Y[s](y):=subs(n=s,Y[n](y)):
Y
n
(y) :=
√
2 sin(ny)
√
π
(7.22)
Statements of orthonormality with their respective weight functions
> w(x):=1:Int(X[m](x)*X[r](x)*w(x),x=0..a)=delta(m,r);
π
0
2 cos(mx) cos(rx)
π
dx = δ(m, r) (7.23)
> w(y):=1:Int(Y[n](y)*Y[s](y)*w(y),y=0..b)=delta(n,s);
π
0
2 sin(ny) sin(sy)
π
dy = δ(n, s) (7.24)
Time-dependent solution
> T[m,n](t):=exp(−gamma/2*t)*(A(m,n)*cos(omega[m,n]*t)+B(m,n)*sin(omega[m,n]*t));
T
m, n
(t) := A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
(7.25)
> T[0,n](t):=exp(−gamma/2*t)*(A(0,n)*cos(omega[0,n]*t)+B(0,n)*sin(omega[0,n]*t));
T
0,n
(t) := A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
(7.26)
Generalized series terms
> u[m,n](x,y,t):=T[m,n](t)*X[m](x)*Y[n](y);
u
m, n
(x,y,t):=
2
A(m, n) cos
ω
m, n
t
+B(m, n) sin
ω
m, n
t
cos(mx) sin(ny)
π
(7.27)
> u[0,n](x,y,t):=T[0,n](t)*X[0](x)*Y[n](y);
u
0,n
(x,y,t):=
A(0,n)cos
ω
0,n
t
+B(0,n)sin
ω
0,n
t
√
2 sin(ny)
π
(7.28)
Eigenfunction expansion
