Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1

381

где

T r C



ф ф

— постоянная времени фильтра.

Записывая эту систему уравнений в координатах

d q

, ,0

синхронного двигателя [256], получим:

T

du

dt

u u u

T

du

dt

u u u

d

q

d d

q

d

q q

ф

ф ф

ф

ф ф















  















  













р

,

(8.36)

где

u

d

ф

;

u

q

ф

;

u

d

;

u

q

— координатные составляющие напря-

жений соответственно фильтра и обмотки якоря ВД.

Из уравнений (8.36) для установившегося режима

du

dt

du

dt

d

q

ф ф

 













0 можно найти, что





tg

ф

  

T



р

. (8.37)

Это равенство указывает, что, в соответствии с формулой

(8.34), разным значениям частоты вращения ротора будут

отвечать разные значения угла отпирания инвертора 

1

.

Только при отсутствии фильтра (

T



0

) будем иметь:

 

ф

  ;  

1



ф

. (8.38)

Из рис. 8.6 видно, что, как для установившегося, так и

для переходного режима, справедливо:

tg

ф ф ф

 

u u

d

q

. (8.39)

В результате линеаризации этого равенства получим:

~

~ ~



ф ф ф

 

n u n u

d

q

1 2

, (8.40)

382

где

n

T

U

m

1

0 0 0

10

 



р

sin cos 

;

n

T

U

m

2

0 0 0

10

 



р

cos sin 

.

Найдем теперь выражение, определяющее приращение

угла нагрузки



. Из формулы для составляющих тока якоря

ВД





i I

d m

 

1

sin   ;





i I

q

m

  

1

cos   (8.41)

будем иметь

~

cos

~

sin

~

   

 



10

1

I

i

I

i

m

d

m

q

. (8.42)

Если использовать уравнение





  

1 1



f

; , например, в

форме из [103], то равенство (8.42) с учетом зависимостей

(8.34) и (8.31) примет вид:

~ ~

~

р

      

c c i c i c U c c

d q m

1 2 3 4 1 5

6

1

ф ф

  . (8.43)

При допущении линейного изменения выходного тока

инвертора на интервале коммутации, когда

  

1

2  , (8.44)

коэффициенты уравнения (8.43) будут равны:

с

1

2

   ;

с

c

I

b

m

2

10

2 1

2

 













cos

sin



 ;

с

c

I

b

m

3

10

2 1

2

 













sin

cos



;

с

d

c

4

 ;

с

e

c

5

 ;

с

c

6

1

2

  .

Принимая во внимание формулы (8.29), (8.34), (8.40),

приращения

~

U

m

1

и

~

 , представленные уравнениями (8.33),

383

(8.43), можно выразить через независимые переменные

6

—

~



i

( ,... )

i

 1 5 ;

~

р

 ;

~

u

d

ф

;

~

u

q

ф

их производные и приращения

сигналов управляющих (внешних) воздействий —

~

u

п

;

~

;

u

fd

н

~



1

ф

.

~

,

~

.

U k

dx

dt

dx

dt

g x

c U h x

m i

i

m i

i

1

6

1

4

1

11

4 1

1

11

  















 















 



(8.45)

где через

x

i

(

i

 1 11,..., ), обозначены соответственно вели-

чины

~



i

( ,... )

i

 1 5 ;

~

р

 ,

~

u

d

ф

,

~

u

q

ф

,

~

u

п

,

~

u

fd

н

,

~



1

ф

.

Формулы для коэффициентов уравнений (8.45) приведены

в [39].

С помощью уравнений (8.45) несложно найти прираще-

ния напряжений якоря

u

d

и

u

q

и записать в линеаризован-

ной форме известные уравнения Парка-Горева, определяю-

щие равновесие напряжений обмоток якоря и индуктора и

вращающих моментов на валу ВД:

m

dx

dt

m

dx

dt

x

m

dx

dt

m

dx

dt

x

dx

dt

x j

i i

i

i i

i

j

ji i

i

11

1

14

4

1

11

41

1

44

4

1

11

1

10

2 3 5 6

 

 



















;

;( , , , ),

(8.46)

где выражения для коэффициентов представлены в [39].

6

Как уже отмечалось, под независимыми переменными понимают-

ся величины, которым отвечают дифференциальные уравнения

первого порядка. Общее число независимых переменных равно

порядку системы дифференциальных уравнений, описывающих

неустановившийся режим ВД.

384

Приводя первое и второе уравнения системы (8.46) к

нормальной форме Коши и линеаризируя дифференциаль-

ные уравнения (8.36), определяющие независимые перемен-

ные

~

u

d

ф

,

~

( , )

u x x

q

ф

7 8

, получим исходную систему дифферен-

циальных уравнений, предназначенную для исследования

статической устойчивости ВД:

dx

dt

x j

j

ji i

i

 







1

10

1 8,( ,..., ). (8.47)

При отсутствии автоматического регулирования управляю-

щих воздействий ( )

x x x

9 10 11

0   статическая устойчивость

ВД будет определяться собственными значениями квадратной

матрицы 

ji

, ( , ,..., ),

i j

 1 8 имеющей восьмой порядок. Если

пренебречь действием фильтра на входе СИФУ инвертора, то

эта матрица будет иметь шестой порядок.

Для разомкнутой системы ( )

x x x

9 10 11

0   приращение

угла выбега ротора (угла нагрузки)



, как видно из уравне-

ний (8.45), (8.47), является линейной комбинацией незави-

симых переменных. По этой причине угол



нельзя рас-

сматривать как независимую переменную, влияющую на по-

рядок характеристического уравнения системы. У синхрон-

ного двигателя с обычным питанием от сети с напряжением

частоты





const

угол



определяется из дифференциаль-

ного уравнения:

d

dt



   

р

, (8.48)

и, следовательно, является независимой переменной.

Àнализ устойчивости ВД, имеющего параметры лаборатор-

ного макета мощностью 2,8 кВт, производился с помощью

ЦВМ по табличному критерию Рауса. Установившийся (на-

чальный) режим вентильно-машинной системы определялся

итерационным методом с использованием магнитной характе-

ристики машины. Исследовалось, прежде всего, влияние

фильтра СИФУ на устойчивость системы. Оказалось, что для

каждого значения нагрузки на валу ВД можно указать такое

385

критическое значение постоянной времени фильтра

T

кр

, что

при

T T



кр

ВД становится статически неустойчивым. Значе-

ния

T

кр

в секундах для ВД со смешанным возбуждением

(

k

fd

c

 1 5, ;

k

fq

c

 0 ) при cos 

1

0 9 , и с различной степенью

нагруженности, а также сведения о влиянии на величину

T

кр

успокоительной обмотки и размера воздушного зазора даны в

табл. 8.2.

Таблица 8.2

Успокои-

тельная

Параметры, о.е.

T

кр

, с. при токах якоря (о.е.)

обмотка

L

ad

L

aq

I

fd

н

0,25 0,5 0,75 1,0 2,5

Есть 0,84

0,51

0,62

1 2, 





10

4

2 2, 





10

4

3 3, 





10

4

4 0, 





10

4

8 3, 





10

4

Есть 0,84

0,51

1,24

1 2, 





10

4

2 3, 





10

4

3 4, 





10

4

4 4, 





10

4

10 





10

4

Нет 0,84

0,51

1,24

1 7, 





10

4

3 3, 





10

4

5 0, 





10

4

6 7, 





10

4

-

Есть 1,68

1,02

1,24

- - -

3 8, 





10

4

-

Есть 1,68

1,02

1,86

- - -

4 7, 





10

4

-

Отсутствие успокоительной обмотки вызывает рост

Т

кр

более чем в 1,5 раза.

При увеличении индуктивностей взаимоиндукции

L

ad

и

L

aq

в 2 раза (это эквивалентно примерно такому же умень-

шению воздушного зазора ВД) наблюдается небольшое сни-

жение (порядка 10%)

Т

кр

.

Опыт показывает, что для устранения коммутационных

«провалов» в напряжении синхронизации СИФУ требуется

фильтр, у которого

T

не менее ( ... )25 50 10

4





c. Поскольку

386

Т

кр

обычно меньше этого значения, то учет фильтра при

анализе устойчивости ВД принципиально необходим, так

как, в противном случае, устойчивая вентильно-машинная

система будет трактоваться как неустойчивая.

Стабилизирующее действие фильтра СИФУ инвертора

можно объяснить с качественной стороны, сравнивая рас-

сматриваемый ВД с ВД, имеющим датчик положения ротора

(ДПР). У такого ВД, как показывают опытные и теоретиче-

ские исследования, обычно не возникает проблемы обеспе-

чения устойчивости при использовании его в разомкнутой

системе электропривода. Характерной его особенностью яв-

ляется постоянство углового параметра



— угла установки

ДПР, который мало отличается от угловой величины:

  

1 1 0

2    



;



I E

m m

.

У рассматриваемого ВД в соответствии с формулами (8.34),

(8.44) имеем для этого параметра выражение:

  

1

ф ф

 . (8.49)

Наличие фильтра с достаточно большой постоянной времени

приводит к ограничению величины варьирования угла 

ф

при отклонении системы из равновесного состояния. Вслед-

ствие этого при 

1

ф

const режим угла



будет приближать-

ся к его режиму у ВД с ДПР. Близость режимов угла



у

обоих типов ВД вызывает одинаковый характер действия ре-

акции якоря, так как осевые составляющие тока якоря

i I

d m



1 1

sin  ;

i I

q m

 

1 1

cos .

Статические и динамические свойства ВД при прочих рав-

ных условиях определяются прежде всего характером дейст-

вия реакции якоря.

387

При отсутствии фильтра на входе СИФУ параметром

управления инвертора будет угол 

1

. Угол



, как видно из

формулы (8.44), определится равенством

  

1

 . (8.50)

Его режим отличается от предыдущего случая, так как

при 

1

 const из формул (8.42), (8.44), (8.50) имеем:

~

cos

~

sin

~



 

  

10

1

2

I

i

I

i

m

d

m

q

,

т.е. при вариации независимых переменных угол



не будет

оставаться постоянным. Можно аналитически показать, что

в рассматриваемом случае при отсутствии регулирования

управляющих воздействий ( )

x x x

9 10 11

0   ВД независимо-

го возбуждения статически неустойчив. В самом деле, при-

менительно к ВД независимого возбуждения (

k k

fd fq

c c

  0 )

при отсутствии фильтра на входе СИФУ (

T



0

), сглажи-

вающего дросселя в цепи постоянного тока инвертора

(

L



0

) и нулевых значениях взаимоиндуктивностей между

перпендикулярными обмотками машины (

L

ij

 0 ) из форму-

лы (8.29) и пояснений к формуле (8.33) будем иметь:

l j i

a a a a i

j i

i i i i

   

    







0 1 5 0 1 5

0 1 2 3

4 4 5 5

, ( ,... ); , ( ,..., );

, ( , , ).



(8.51)

С помощью выражений из примечаний к формулам

(8.46), (8.47), учитывая (8.51), можем определить диагональ-

ные члены матрицы 

ji

:





 

11 11 10

10

10 0

0

10 0

0 5 













 













a U

I

b r

R

k

m

cos

sin cos sin sin,   ;

388





 

44 44 10

10

10 0

0

10 0

05 













 













a U

I

b r

R

k

m

sin

cos sin cos cos,   ;



22 22

 

a r

fd

н

; 

33 33

 

a r

d

к

; 

55 55

 

a r

q

к

; 





66

0

 













p

J

M

с

р

,

где

 

a L L L L L

d ad fd kd

11

1

1 1 1



   















  н

;

 





a L L L L L

fd fd ad kd

22

1

1 1 1



   



н н  

;

 

a L L L L L

d d ad fd

33

1

1 1 1



   















к к н  

;

   

a L L L L

q aq q

44

1 1

1

1 1



  













 



 к

;

   

a L L L L

q kq aq

55

1 1

1

1 1



  













 



к  

.

Если отвлечься от сравнительно небольшого различия

сверхпереходных индуктивностей обмоток и принять

a a L i

ii d

 





11

1 1 2 5, , ,..., , то для следа матрицы 

ji

полу-

чим выражение:

S

p ii

i

 







1

6

1



L

d

U

I

b

m

10

05

cos

sin

























,

    







R

k

r r r r

m

fd d q

0

10

2cos

н к к

















p

J

M





c

р

0

.

В соответствии с критериями Гурвица необходимым ус-

ловием статической устойчивости ВД является выполнение

неравенства

S

p

 0 . Учитывая реальные значения активных

сопротивлений цепей обмоток двигателя, можно утверждать,

389

что в зоне его рабочих нагрузок и при малых значениях





M

c

р













0

(например, при независимости статического момен-

та сопротивления нагрузки на валу двигателя от скорости его

вращения)

S

p

 0 .

Следовательно, действительно, в рассматриваемом случае

ВД статически неустойчив.

Опыт работы с лабораторной моделью ВД и некоторые

специально проведенные эксперименты подтверждают полу-

ченные результаты.

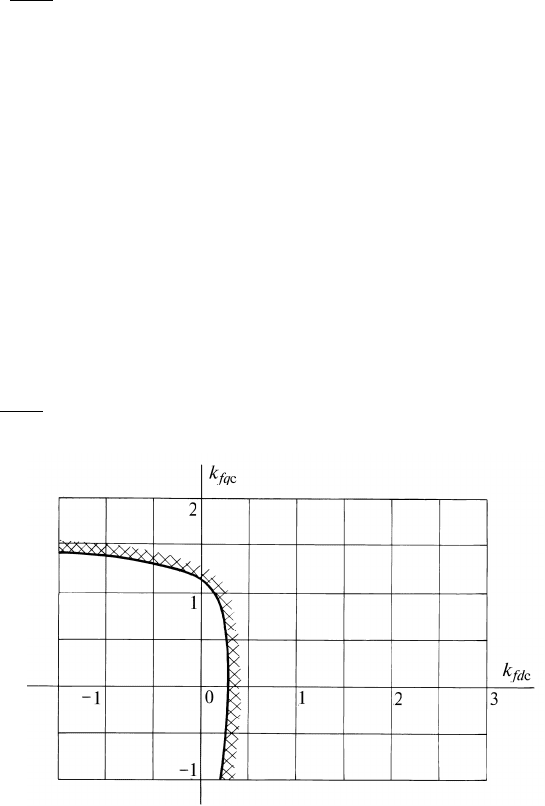
Область статической устойчивости ВД в плоскости коэф-

фициентов приведения токов последовательных обмоток воз-

буждения к обмотке якоря

k

fd

c

и

k

fq

c

(штриховка границы

обращена внутрь области устойчивости), найденная с помо-

щью ЦВМ для ВД мощностью 2,8 кВт (его параметры приве-

дены в [40]), работающего при номинальных значениях тока

якоря, частоты вращения ротора с cos cos

н

 

1

 в разомк-

нутой системе регулирования ( )

x x x

9 10 11

0   при





M

c

р

 0 представлена на рис. 8.7.

Рис. 8.7. Область статической устойчивости вентильного двигателя

390

Коэффициенты

k

fd

c

и

k

fq

c

пропорциональны числам витков

последовательных обмоток возбуждения

fd

c и

fd

н . Поло-

жительные значения

k

fd

c

соответствуют согласному включе-

нию обмоток

fd

c и

fd

н , а положительные значения

k

fq

c

—

встречному включению обмоток

fq

c и

q

. Для обеспечения

режима полной компенсации МДС якоря по обеим осям

указанные коэффициенты у рассматриваемого ВД при

cos cos

н

 

1

0 9  , (опережающем) должны быть:

k

fd

c

 0 55, ;

k

fq

c

 1 3, . Как видно из рис. 8.7, эти значения

соответствуют устойчивому ВД.

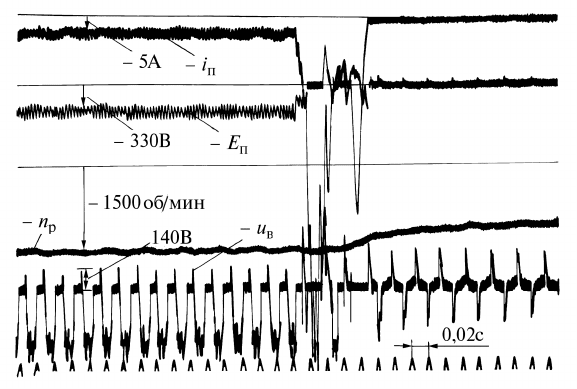
Рис. 8.8. Переходный процесс при скачкообразном уменьшении

постоянной времени фильтра СИФУ инвертора:

i E u

п п в

, ,

— вход-

ной ток, противоЭДС и напряжение вентиля инвертора;

n

p

— ско-

рость вращения двигателя

Осциллограмма переходного процесса, вызванного скач-

кообразным уменьшением постоянной времени фильтра

Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1

Подождите немного. Документ загружается.