Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1

Подождите немного. Документ загружается.

361

ными, установившийся режим и матрица монодромии рас-

считываются одновременно.

Как известно [295], для обеспечения асимптотической

устойчивости системы (8.4) необходимо и достаточно, чтобы

собственные значения матрицы монодромии





X T

— муль-

типликаторы данной системы — на комплексной плоскости

лежали внутри единичной окружности.

Нахождение матрицы монодромии является, вообще го-

воря, начальным этапом приведения системы линейных

дифференциальных уравнений с периодическими коэффици-

ентами (8.4) к системе линейных дифференциальных уравне-

ний с постоянными коэффициентами:

  ,

где

 

 

— постоянная матрица (ее элементы не

зависят от времени).

Старые переменные

связаны с новыми

уравнением





x y

 

, в котором













 

t t t

 

exp — неособенная пе-

риодическая матрица — матрица Флоке, причем





 

 

t T t

 

Если собственные значения матрицы монодромии —

мультипликаторы — обозначим через 

(

j n

 1 2, ,... ), то

собственные значения постоянной матрицы 

(характери-

стические показатели исходной системы (8.4)) будут равны

[124]:





  

j j j

 

ln Àrg .

Отсюда видно, что при 

 1 имеем Re 

 0 . Из этих не-

равенств следует необходимое и достаточное условие асим-

птотической устойчивости исходной периодической системы

(8.4) — модули ее мультипликаторов должны быть меньше

единицы.

362

Расчет статической устойчивости производился для ВМ,

работающей двигателем, мощностью 2,8 кВт с параметрами,

приведенными в [38]

Как и в [38], где расчет устойчивости выполнялся при

описании процессов в ПЧ непрерывными функциями и при

пренебрежении высшими гармоническими токов и напряже-

ний ВМ, определялась граница статической устойчивости

системы в плоскости коэффициентов

— коэффи-

циентов приведения токов последовательных обмоток возбу-

ждения по осям

к обмотке якоря. Эти коэффициенты

пропорциональны числам витков последовательных обмоток

возбуждения. Для всех вариантов расчетов рассматривалась

также устойчивость системы

d dtx x

 

, (8.6)

производной от исходной системы (8.5), где:







— (8.7)

постоянная матрица.

Полученные данные свидетельствуют, что для номиналь-

ной частоты вращения ВМ дискретность процессов ПЧ (т.е.

учет также влияния всего спектра высших временных гармо-

нических) практически не влияет на конфигурацию области

устойчивости в плоскости коэффициентов

. При-

чем мультипликаторы системы (8.4) и (8.6) близки друг к

другу (см. табл. 8.1), что и подтверждается опытными дан-

ными. При представлении ПЧ непрерывной моделью неус-

тойчивая зона на пониженных частотах для аналогичных па-

раметров ВМ не обнаруживается.

Успокоительная обмотка на полюсах индуктора была представле-

на двумя эквивалентными контурами.

363

Таблица 8.1

Система

ДУ

Частота

вращения

М у л ь т и п л и к а т о р ы

(о.е.) 1 2 3 4 5 6 7 8

(8.4) 1,0 1,15



0,0499

0,718 0,994 0,853+

0,0687

0,853+



0,0687

0,806+

0,299

0,806+



0,299

(8.6) 8,53



5,37



0,724 0,802 0,979 0,994 0,675+

0,166

0,675



0,166

(8.4) 0,1 2,1



8,24



0,709 0,874 0,792+

0,0771

0,792



0,0771

0,995 1,12

(8.6) 2,51



3,17



0,702 0,866 0,805+

0,0384

0,805



0,0384

0,995 1,15

363

364

Близость друг к другу мультипликаторов систем (8.4) и

(8.6) указывает, что построение границ устойчивости в пер-

вом приближении можно производить, используя постоян-

ную матрицу коэффициентов (8.7) вместо периодической

(8.5). Этот прием позволяет существенно упростить анализ

устойчивости, так как исключается операция численного ин-

тегрирования системы ДУ (8.4) для определения матрицы

монодромии и используются хорошо разработанные методы

исследования систем ДУ с постоянными коэффициентами, в

том числе матричные, алгебраические и табличные критерии

устойчивости.

Численные расчеты также показывают, что импульсные сла-

гаемые с дельта-функцией в приращениях напряжения на вен-

тилях (5.32), обусловленные вариацией угла коммутации, прак-

тически не оказывают влияния на значения мультипликаторов

с наибольшими модулями, т.е. расположенных вблизи единич-

ной окружности. Пренебрежение этими слагаемыми изменяет

значения указанных мультипликаторов на величину, не превы-

шающую десятые доли процента. Мультипликаторы, располо-

женные ближе к центру окружности с единичным радиусом,

изменяются более значительно. Такой характер воздействия

импульсных слагаемых формулы (5.32) на мультипликаторы

системы позволяет в большинстве случаев отказаться от учета

этих слагаемых при анализе устойчивости ВМ.

Выводы

1. Для номинальной частоты вращения вентильной ма-

шины дискретность процессов преобразователя частоты

практически не оказывает влияния на конфигурацию облас-

ти статической устойчивости. Для низких частот вращения

это влияние более значительно.

2. Замена периодической матрицы коэффициентов ис-

ходной линеаризованной системы дифференциальных урав-

нений ее усредненным приближением в виде матрицы с по-

стоянными коэффициентами позволяет существенно упро-

стить анализ статической устойчивости вентильной машины

без существенной потери точности, так как мультипликаторы

периодической и постоянной матриц близки друг к другу.

365

3. Импульсные функции Дирака в коэффициентах перио-

дической матрицы однородной системы линеаризованных

дифференциальных уравнений оказывают влияние только на

мультипликаторы, расположенные ближе к центру единич-

ной окружности. Поэтому пренебрежение этими функциями,

в целях упрощения анализа, практически не влияет на пока-

затели статической устойчивости.

8.3. Исследование статической устойчивости вентильных

машин при пренебрежении высшими гармоническими то-

ков и напряжений обмоток

8.3.1. Общие замечания

Как показывают данные предыдущего параграфа, высшие

гармоники токов и напряжений обмоток ВМ оказывают

сравнительно слабое воздействие на показатели статической

устойчивости. Только в области малых частот вращения их

влияние проявляется заметным образом. Поэтому анализ

особенностей воздействия разнообразных конструктивных и

схемных факторов на устойчивость в малом может произво-

диться без учета высших временных гармоник ВМ.

8.3.2. Статическая устойчивость вентильной машины

постоянного тока с датчиком положения ротора.

В вентильных машинах постоянного тока роль механиче-

ского коллектора выполняет полупроводниковый коммута-

тор, управление вентильными элементами которого произво-

дится с помощью датчика тактовой синхронизации. Одним

из наиболее распространенных полупроводниковых коммута-

торов, позволяющим получить широкий диапазон регулиро-

вания частоты вращения вентильного двигателя (ВД), явля-

ется инвертор тока с естественной или, в общем случае, с

искусственной коммутацией, синхронизируемый датчиком

положения ротора (ДПР) (рис. 8.1). Полупроводниковый

коммутатор этого типа обеспечивает сравнительную простоту

пуска и рекуперативного торможения ВД.

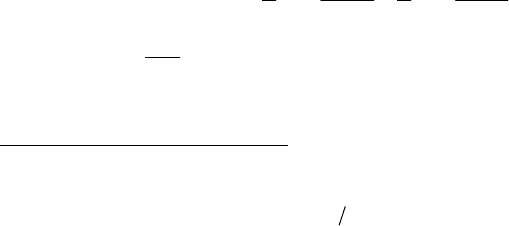
366

Угол управления инвертором



, выставляемый с помо-

щью ДПР, соответствует углу сдвига щеток с геометрической

нейтрали у машин постоянного тока с механическим коллек-

тором

. При значениях угла



, отличных от нуля, возникает

продольная составляющая МДС якоря, направление дейст-

вия которой определяется знаком этого угла.

Важным средством компенсации реакции якоря и фор-

мирования требуемых статических и динамических характе-

ристик ВД является применение смешанного возбуждения с

использованием последовательных обмоток возбуждения по

продольной и поперечной осям машины [36]. Выполнение,

например, последовательной поперечной (компенсационной)

обмотки возбуждения позволяет выдержать постоянство на-

пряжения и коэффициента мощности на зажимах обмотки

якоря при изменении нагрузки ВД.

Необходимым условием принципиальной возможности

физической реализации тех или иных статических характери-

стик машины является ее устойчивость при малых прираще-

ниях переменных (статическая устойчивость).

Исходные уравнения ВД записываются при следующих

допущениях: токи и напряжения на входе и выходе инверто-

ра не содержат высших гармонических; распределение МДС

и магнитной индукции в воздушном зазоре ВД синусоидаль-

но. Эти уравнения имеют вид:

u k u k u k

q d fd

п c

    

1 2

 

 

    

R R R R i

fd fq

c c эк п

; (8.8)

Угол установки ДПР



близок к углу

  

1 1 0

2    



;



I E

m m

(см. рис. 8.3),

где



- угол коммутации вентилей инвертора.

367

r i

fd fd

н н

 



; (8.9)

0  

r i

d d



к к

; 0  

r i

q q



к к

; (8.10)

 

p i i M

d q q d



 

  

; (8.11)

где

3 3





cos ;

3 3





sin ; (8.12)

r i

d q

   



 

; (8.13)

r i

q d

   



 

; (8.14)

экв

— эквивалентное активное сопротивление, учиты-

вающее процесс коммутации тока на выходе инвертора;

— коммутационная индуктивность, определяющая ве-

личину эквивалентного активного сопротивления

экв

;

— активное сопротивление и индуктивность сглажи-

вающего дросселя;

;

— активные сопротивления последовательных

обмоток возбуждения;

— напряжение и ток на входе инвертора.

В записанной системе уравнений токи

(

 1 4,... ; этим

числовым индексам соответствуют по порядку буквенные

индексы — п, н, к , к

fd d q

) могут рассматриваться как незави-

симые переменные.

Потокосцепления всех обмоток 

(

 1 7,... ; числовыми

индексами обозначены соответственно обмотки —

368

q fd d q d fd fq

, , ,н,к , к c, c ) ВД, имеющего в общем случае насы-

щенную магнитную цепь, являются нелинейными функция-

ми токов

. В точке установившегося режима для малых

приращений потокосцеплений



и токов

справедливо



i i j j



l i

, (

i j

 1 7 1 4,... ; ,... ), (8.15)

где

i j



















— дифференциальные индуктивности обмоток

ВД.

Для удобства линеаризации уравнений (8.8)—(8.14) при-

мем в качестве независимых переменных вместо четырех то-

ков

первые четыре потокосцепления



. Выбор одним из

независимых переменного потокосцепления



(



) вме-

сто



(



) продиктован возможностью иметь при нуле-

вом угле управления инвертора (

0 ) такую же форму за-

писи линеаризованного уравнения (8.8), как и у обычной

машины постоянного тока.

Токи

и остальные потокосцепления



(

 5 6 7, , ) мо-

гут быть выражены через независимые потокосцепления:

i a

j ji i

  ,

i j

, ,... 1 4 , (8.16)

 

i ij j



 5 6 7, , ;

 1 4,... , (8.17)

где

a l

ji ij



1

i j

, ,... 1 4 , (8.18)

ik kj

l a





 5 6 7, , ;

 1 4,... . (8.19)

Линеаризованные, с учетом формул (8.16), (8.17), диффе-

ренциальные уравнения (8.8)—(8.11) будут иметь вид

369

u u

i i i fd i

~ ~ ~



        





5 1 2н п

; (8.20)



    





, (8.21)

где

 1 4,... ;

выражения для коэффициентов 

, 

приведены в [38].

При отсутствии автоматического регулирования входного

напряжения инвертора (

 0 ) и напряжения независимой

обмотки возбуждения (

 0 ) статическая устойчивость

ВД определяется собственными значениями матрицы 

Расчеты статической устойчивости при

~ ~

u u

п н

  





производились на ЦВМ для вентильной машины мощностью

2,8 кВт с параметрами, приведенными в [38]

. Границы ста-

тической устойчивости в плоскости коэффициентов

при номинальных значениях тока якоря и частоты вра-

щения ротора и при различных углах управления инвертора

представлены на рис. 8.2.

Для режимов ВД, при которых угол

  

2  

становился

меньше

20

(здесь принято, что для опережающего тока якоря



0

, для отстающего —



0

) вводилось допущение о мгно-

венной коммутации вентилей инвертора. Реализация этих режимов

возможна при искусственной коммутации инвертора.

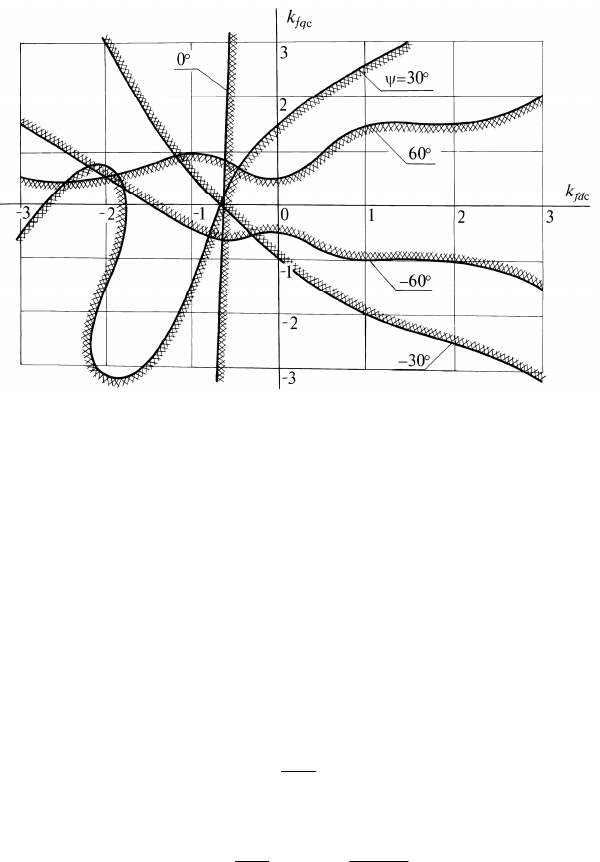
370

Рис. 8.2. Области устойчивости вентильной машины в плоскости

коэффициентов приведения токов последовательных обмоток воз-

буждения (штриховка границ обращена внутрь областей устойчиво-

сти)

Коэффициенты приведения токов последовательных обмоток

возбуждения к обмотке якоря —

— пропорцио-

нальны числам витков обмоток

c и

c . Положительные

значения

соответствуют согласному включению обмо-

ток

c и

н , а положительные значения

— встречно-

му включению обмоток

c и

. Для обеспечения режима

полной компенсации МДС якоря по обеим осям указанные

коэффициенты должны иметь значения [36]:

 

sin   

, (8.22)

 

aq aq

cos sin 













  





1 1

, (8.23)