Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1

Подождите немного. Документ загружается.

201

В этих точках 

и 



примерно равны своим средним зна-

чениям на интервале (3.95). Так кривые (рис.3.6) показыва-

ют, что при малых и средних насыщениях коэффициенты



примерно одинаковы.

2. Коэффициенты насыщения для индуктивностей само-

и взаимоиндукции обмоток по одной и той же оси в общем

случае неодинаковы, например, из формул (3.91), (3.93),

(3.94) видно:

k k k

d df f

   

  . Это отличие обусловлено не-

совпадением форм кривых МДС соответствующих обмоток.

Указанная особенность приводит к появлению зависимости

от насыщения у коэффициентов приведения токов обмоток

индуктора к обмотке якоря. Так, в частности, из равенства

~ ~

L i L i

adf f ad f

  следует:

wk k

w k

i f

w ad

f f











В результате приведенные к обмотке якоря динамические

индуктивности будут зависеть от нескольких коэффициентов

насыщения. Например:

~ ~ ~



 

L k L L

k k

ff i j ff ad

b ad

d f

 



  

Индуктивности взаимоиндукции между перпендикуляр-

ными обмотками целесообразно выразить в долях ненасы-

щенных значений индуктивностей самоиндукции обмотки

якоря

или

, обусловленных основным потоком взаи-

моиндукции воздушного зазора. Это облегчит численную

оценку таких индуктивностей, особенно при их приведении

к обмотке якоря. В частности, формуле (3.85) может быть

придан вид:

L L C

adq ad adq

   , (3.96)

где

 

C k sin

adq ad x



















  









,   

 0 0



min

202

Коэффициент

adq

, как видно из рис. 3.6, для номинального

режима составляет 0,06; при ослаблении поля возбуждения

на 25%, но при прежней (номинальной) токовой нагрузке

обмотки якоря увеличивается до значения 0,09.

3.6. Схемы замещения синхронной машины, учитывающие

реальные контуры демпферной обмотки

Представление синхронной машины электромагнитными

схемами, в которых демпферной обмотке соответствуют два

эквивалентных контура по осям

, в ряде случаев оказы-

вается недостаточно точным или совершенно неприемле-

мым. Так расчет потерь и нагрева ротора при асинхронном

ходе, в синхронном режиме с наличием высших гармониче-

ских в кривых напряжения питания обмоток статора и воз-

буждения требует учета как реальных электрических конту-

ров ротора, так и эквивалентных, соответствующих вихревым

токам в стали статора и ротора.

Нестандартное расположение стержней демпферной об-

мотки, неоднородность их материала или нарушение целост-

ности некоторых из них также вызывают необходимость оп-

ределения действительного токораспределения в контурах

ротора. Расчет этого токораспределения можно произвести

путем нахождения токов контуров успокоительной обмотки,

симметричных относительно осей

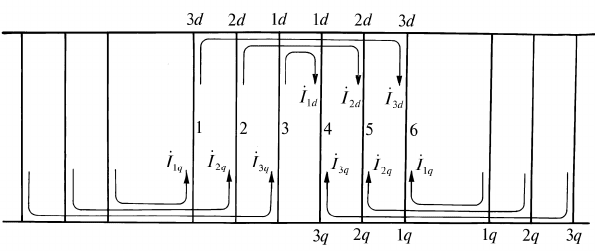
(рис. 3.7).

Рис. 3.7. К расчету токораспределения в элементах демпферной об-

мотки

203

Действительные токи стержней и короткозамыкающих пере-

мычек могут быть найдены суммированием контурных токов.

Анализ распределения токов и потерь в отдельных эле-

ментах успокоительной обмотки и обмотке возбуждения, ис-

следование влияния параметров обмоток на характер этого

распределения существенно облегчаются при использовании

электрических схем замещения сопротивлений синхронной

машины по осям

Произведем обоснование этих схем.

Считаем обмотки ротора приведенными к трехфазовой

обмотке статора. Будем рассматривать обмотки по оси

ма-

шины, так как соответствующий анализ по оси

аналогичен,

за исключением того, что по этой оси отсутствует обмотка

возбуждения.

Для потокосцеплений обмоток запишем выражения:



d d d a d d a d d and nd ad f

L i L i L i L i L i

     

1 1 2 2

... , (3.97)



1 1 11 1 12 2 1 1

d a d d d d d d nd nd df f

L i L i L i L i L i

     ... , (3.98)

.................................................................................



nd and d n d d n d d nnd nd ndf f

L i L i L i L i L i

     

1 1 2 2

... , (3.99)



f ad d f d d f d d fnd nd ff f

L i L i L i L i L i

     

1 1 2 2

... . (3.100)

Уравнения для напряжений

контуров демпферной об-

мотки и контура обмотки возбуждения

1 11 1 12 2 1

    

p r i r i r i

d d d d d nd nd

 ... , (3.101)

..........................................................

1 1 2 2

    

p r i r i r i

nd n d d n d d nnd nd

 ... , (3.102)

u p r i

f f f f

  (3.103)

можем записать в развернутой форме с учетом того, что по

физическим соображениям [87]

204

L L L L

iid iid iid iid

  

 с л

;





i n

 1 2, ,... , (3.104)

L L L

ikd iid iid

 

 л

;





i k

 , (3.105)

L L

idf iid





, (3.106)

r r r

iid iid iid

 

c л

r r

ikd iid



;





i k

 , (3.107)

где

iid

— полная собственная индуктивность

— контура

демпферной обмотки;

iid



iid

— ее составляющие, обусловленные со-

ответственно: магнитным полем, пересекающим воздуш-

ный зазор; магнитным полем рассеяния обоих стержней

— контура; магнитным полем, сцепленным с обоими ло-

бовыми частями

-контура;

iid

— активное сопротивление

-контура демпферной

обмотки;

iid

— его составляющие, обусловленные соответ-

ственно сопротивлением двух стержней и двух лобовых

перемычек

-контура.

Равенство (3.106), справедливое при предложении, что

магнитная связь между обмотками

осуществляется по-

током воздушного зазора, обычно используется в практиче-

ских расчетах [87,122].

В результате из (3.101)—(3.103) получим:





1 11 11 1

   

pL i pL r i

a d d d d d

c c













      

p L L r i i i pL i

d d d d d nd d f

 11 11 11 1 2 11л л

... , (3.108)













2 22 2 11 11 11

      

pL i pL r i p L L r

a d d d d d d d d

c22 c л л

























          

i i i p L L L L r r

d d nd d d d d d d

1 2 22 11 22 11 22 11

...

  л л л л





    

i i i pL i

d d nd d f

2 3 22

...



, (3.109)

205













3 33 3 11 11 11

      

pL i pL r i p L L r

a d d d d d d d d

c33 c л л

























          

i i i p L L L L r r

d d nd d d d d d d

1 2 22 11 22 11 22 11

...

  л л л л





    

i i i

d d nd

2 3

...





















      

p L L L L r r

d d d d d d

 33 22 33 22 33 22л л л л





    

i i i pL i

d d nd d f

3 4 33

...



, (3.110)

....................................................................................................





U pL i pL i i i

f ad d d d d nd

     

11 1 2

...

 

  





        

 

p L L i i i p L L i

d d d d nd nnd

n n d

  



22 11 2 3

1 1

... ...













    

p L L L L r i

nnd ff nnd f f f

   

, (3.111)

где



— составляющая собственной индуктивности обмот-

ки возбуждения, обусловленная магнитным потоком в

воздушном зазоре;



— индуктивность рассеяния обмотки возбуждения

(без дифференциального рассеяния), обусловленная маг-

нитным потоком, замыкающимся вне воздушного зазора.

Если введем в рассмотрение индуктивности дифференци-

ального рассеяния контуров успокоительной обмотки, обу-

словленные пространственными высшими гармоническими

индукции в воздушном зазоре:

L L L

iid iid aid

 



;





i n

 1 2, ... , (3.112)

то уравнения (3.108)—(3.111) можно представить в виде:





1 1 2

      

pL i i i i i

a d d d d nd f

...













     

pL r i p L L r

d d d d d d

c11 c д л л11 1 11 11 11

206





    

i i i pL i

d d nd d f

1 2 11

...

, (3.113)





1 1 2

      

pL i i i i i

a d d d d nd f

...









       

p L L i i i i i

a d a d d d d nd f

2 1 2 3

...













     

pL r i p L L r

d d d d d d

c22 c д л л22 2 11 11 11





    

i i i

d d nd

1 2

...





 





 





      

p L L L L r r

d d d d d d

д д л л л л22 11 22 11 22 11













      

i i i p L L L i

d d nd d d d f

2 3 11 22 11

...

д д д

, (3.114)









1 1 2 2 1

        

pL i i i i i p L L

a d d d d nd f a d a d

...





      

i i i i i

d d d nd f

2 3

...









       

p L L i i i i i

a d a d d d d nd f

3 2 3 4

...













     

pL r i p L L r

d d d d d d

c33 c д л л33 3 11 11 11





    

i i i

d d nd

1 2

...





 





 





      

p L L L L r r

d d d d d d

д д л л л л22 11 22 11 22 11





    

i i i

d d nd

2 3

...





 





 





      

p L L L L r r

d d d d d d

д д л л л л33 22 33 22 33 22

















        

i i i p L L L L L i

d d nd d d d d d f

3 4 11 22 11 33 22

...

д д д д д

(3.115)

...................................................................................................









U pL i i i i i p L L

f a d d d d nd f a d a d

        

1 1 2 2 1

...





      

i i i i i

d d d nd f

2 3

... ...

 









...    



p L L i i i

and

a n d

d nd f

207













        

p L L i i pL i i i i

d d d f d d d nd f

a an д11 1 2

...





 

p L L

d d

д д22 11





i i i i

d d nd f

2 3

    ...

  









    

 

...

p L L i i

nnd

n n d

nd f

д 1 1













   

p L L pL r i

ff nnd f f f

д д 

, (3.116)

где

L L L

ff ff ad

 



— индуктивность дифференциального

рассеяния обмотки возбуждения.

Электрическая схема замещения для операторного сопро-

тивления синхронной машины по продольной оси, приве-

денная на рис. 3.8, получена с помощью формул (3.113)—

(3.116). В частности, при определении распределения тока

высших временных гармонических частоты



нужно в ней

сделать подстановку

p jk

  .

При расчете токов ротора в установившемся асинхрон-

ном режиме требуется подстановка

p j s

  .

В соответствии с (3.116) для цепи возбуждения необходи-

мо просуммировать падения напряжения на индуктивных

сопротивлениях дифференциального рассеяния. Для выпол-

нения этого требования в схеме замещения используется

гальваническая развязка в виде трансформаторных связей с

коэффициентом трансформации, равным единице. В про-

тивном случае сопротивления лобовых участков демпферных

контуров оказались бы замкнутыми накоротко. При этом

предполагается, что указанные трасформаторные связи осу-

ществляются с помощью идеальных трасформаторов, у кото-

рых потери активной и реактивной мощности отсутствуют.

Подобная схема замещения для асинхронного режима син-

хронной машины была предложена А.Ранкиным [303].

Наличие трасформаторных связей у ветвей роторных

контуров делает схему замещения несколько неудобной

для расчетов. Если в качестве взаимных индуктивностей

контуров принять не индуктивности, связанные с первой

пространственной гармоникой поля, а индуктивности

вида

iid



, обу-

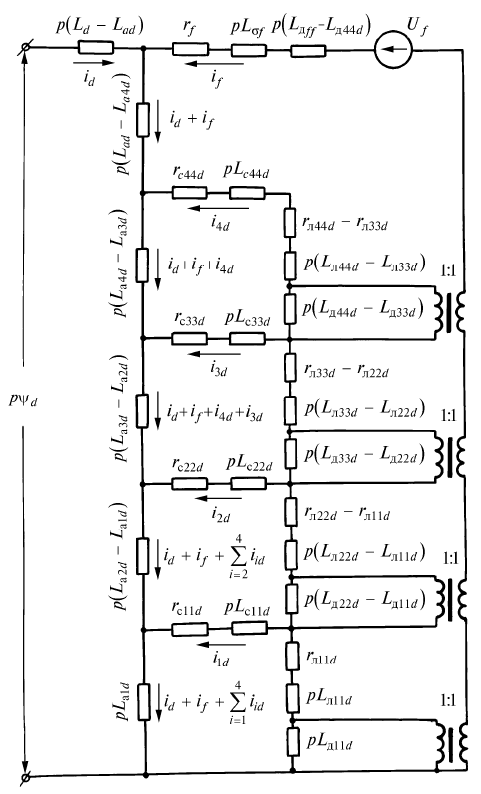
208

Рис. 3.8. Электрическая схема замещения операторного сопротив-

ления синхронной машины по продольной оси с трансформатор-

ными связями между ветвями роторных контуров

209

словленные полным потоком воздушного зазора, и перене-

сти на них трансформаторные связи, то получим схему за-

мещения, на наш взгляд, более удобную для расчета токов

ротора. Это связано с тем, что в ряде случаев гармонический

состав тока статора





i i

d q

; синхронной машины, работающей

совместно с преобразователем частоты, либо уже известен,

либо находится с достаточной точностью путем использова-

ния простых схем замещения синхронной машины, в кото-

рых успокоительная обмотка представлена двумя эквива-

лентными контурами. Тогда предлагаемая схема замещения

(рис. 3.9) позволит сравнительно легко найти распределение

тока высших гармонических по реальных обмоткам ротора и,

тем самым, определить дополнительные потери в них.

В основе новой схемы замещения лежат уравнения

(3.108)—(3.111), только в них потокосцепления взаимоиндук-

ции от тока статора

записываются через некоторые рас-

четные токи





i n f

 12, ,... , , прямо пропорциональные току

L i L i

a d d d d

1 11





, (3.117)





L i L i L L i

a d d d d d d d

2 11

22 11

  

  

, (3.118)









L i L i L L i L L i

a d d d d d d d d d d

3 11

22 11

33 22

    

    

, (3.119)

.................................................................................





  





L i L i L L i L L i

and d d d d d d nnd

n n d

     

 

   



22 11

1 1

... ,(3.120)

  









L i L i L L i L L i

ad d d d nnd

n n d

ff nnd d

     

 

 



 11

1 1

... ,(3.121)

где

 ;





i n

 1 2, ... ,

a d





, (3.122)

  

 

L L

i n

iid

i i d

aid

a i d







 





 1 1

2 3; , ,... , (3.123)

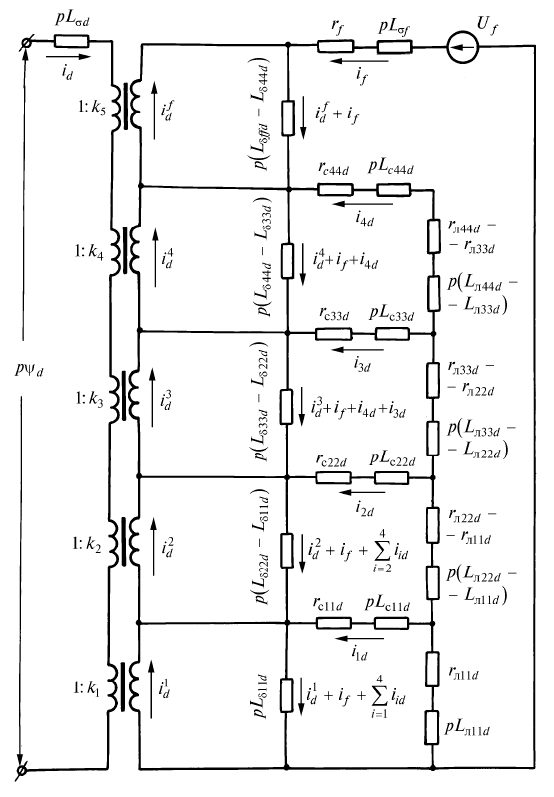
210

Рис. 3.9. Электрическая схема замещения операторного сопротив-

ления синхронной машины по продольной оси с трасформаторны-

ми связями на входе