Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1
Подождите немного. Документ загружается.

171
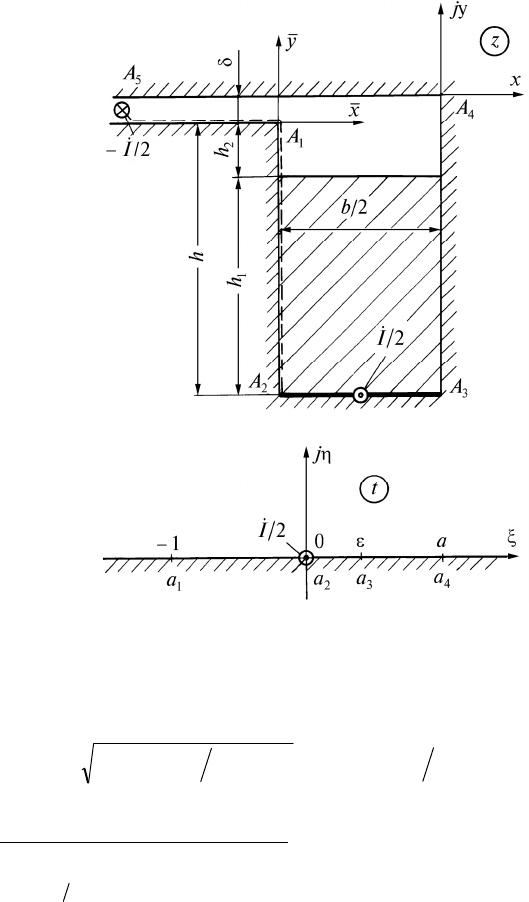
Рис. 3.3. К аналитическому расчету поля и параметров проводника
в пазу
и воспользуемся приближенным равенством
2
1 1
2 2 2
a
1 1 2
2 2 2
a
.
2
Это равенство, обусловленное малостью
,
справедливо для па-
зов с h b
1 1 5.. . ,
.
172
В результате интегрирования (3.25) получим
z
a a
z
2 1 1
2
1
1
arctg ln ,
(3.26)
где
z
a
a a a
a a
2 1
1
2
2
2 2
arctg .
Полагая, что
a
, из уравнения (3.26) можно найти:
4 1 1 2
a a a h a a
( ) exp arctg .
Видим, что с ростом глубины паза
h
постоянная
a
3
стре-
мится к нулю. Специальный анализ уравнения (3.26) показы-
вает, что при
h
b
и
a
0 2 400, ... имеем
a
3
0 001 , . Счи-
тая в дальнейшем, что
h b
1 , можем в (3.25), (3.26) при-
нять:
z
0
. В этом случае для постоянной
a a
4
спра-
ведливо [174]:
a b
2
2
.
Бесконечно тонкая токовая полоса на дне паза в плоско-
сти
z
(рис. 3.3) с током
I
2 преобразуется в линейный про-
вод, расположенный в начале координат плоскости
t
. При
этом комплексная потенциальная функция для МП этого
провода имеет вид:
W t U t
max
ln
м
. (3.27)
Потенциальное МП в пазу первого источника (МП, обуслов-
ленное заданным скалярным магнитным потенциалом гра-
ниц немагнитной области :
U
max
м
на участке
A A A
5 1 2
, нуль
на
A A A
5 1 2
) с учетом формул (3.25), (3.27), равно:
173
H j
dW t
dz
j
dW t
dz
dt
dz
j
U
p
max
м
. (3.28)
В системе координат с началом в точке
A
1
рис. 3.3 (как и на
рис. 3.1) из формулы (3.28) несложно получить выражение
для компоненты
H
px
этого поля в области паза с
~
,
y h b
2
0 5 1 :
exp
~
cos
~
exp
~
cos
~
H
U
b
n y b x b
an y b x b
px
max
2
1 2 2
1 2 2
м
, (3.29)
где
n a a a a
2 1 2( ) exp arctg . (3.30)
Подставляя (3.29) в формулу (3.12) и производя в последней
двукратное интегрирование, получим:
1 1 2
1
2
cos
m h a a n
, (3.31)
где
exp
sin cos exp
4
4
4 4
2
2
1 1 1
h b
b
b h h h b
.
Видим, что при равномерном потенциальном МП паза, ко-
гда
n
0
и, как следствие,
H I b
px
, формула (3.31) сов-
падает с (3.14). После подстановки (3.31) в (3.19), учитывая,
что
x H x h U
px
max
~
,
2
2
м
,
найдем для комплексного сопротивления проводника
174
Z
h a a n
b h a
a
a an h b
п
cos
sin
exp
1
2
1
2
2
1 2
1 1
1 4
.
(3.32)
При
n
0
формула (3.32) принимает известный вид (3.20). Ее
отличие от (3.20) связано, прежде всего, с непостоянством ком-
поненты напряженности МП паза
H
px
по координате
~
x
при
~
y
const , характеризуемом коэффициентом
n
. Чем больше
n
,
тем сильнее ослабляется
H
px
на середине оси паза. Однако ука-
занная неоднородность, как видно из формулы (3.29), быстро
уменьшается при погружении в паз (при росте модуля коорди-
наты
~
y
). Поэтому разница в расчетах по формулам (3.20) и
(3.32) будет тем больше, чем ближе верхняя сторона проводника
к воздушному зазору (чем меньше размер
h
2
). Численные рас-
четы показывают, что использование формулы (3.20) для опре-
деления электрического сопротивления проводника при
h b
2
0 5 , может привести к погрешности в несколько процен-
тов, причем величина этой погрешности увеличивается с рос-
том частоты переменного тока.
При наличии пазов с меньшими, чем в рассмотренном
примере, значениями относительной глубины
h b
и размера
h b
2
, следует обратиться к общей формуле (3.19).
С помощью формул (3.15), (3.29) можем найти также объ-
емную плотность магнитных зарядов как функцию коорди-
нат
~
x
;
~
y
:
sin
~
м м
2 1
0
2 2
n a U b x
max
exp
~
cos
~
sin
~
exp
y y h y h h
2 2 2
,
где 2
b
.
Как уже отмечалось, значения координаты
~
x
в этой формуле сле-
дует рассматривать для всей оси
~
x
. Видим, что функция
175
~
,
~
м м
x y
имеет по переменной
~
x
пространственный период,
равный ширине паза
b
, и внутри паза принимает нулевые значе-
ния на продольной оси и стенках (при
~
; ;
x b b
0 2 ).
Выводы:
1. Предложена методика расчета квазистационарного
МП проводника в пазу, основанная на расчленении МП на
потенциальную и дополнительную составляющие, причем
первая находится средствами теории функций комплексного
переменного, а вторая — на основе решения обыкновенного
дифференциального уравнения второго порядка как краевой
задачи.
2. Показано, что для симметрично расположенного про-
водника в пазу объемные и поверхностные магнитные заря-
ды имеют нечетный периодический характер распределения
относительно продольной оси паза и не участвуют в переда-
че суммарного количества энергии электромагнитного поля в
указанный проводник. Определение комплексного электри-
ческого сопротивления такого проводника может произво-
диться по данным расчета МП, задаваемого только скаляр-
ным магнитным потенциалом ферромагнитных границ паза.
3.3. Обобщенная форма индуктивности пазового рассеяния
Как известно, расчет индуктивности пазового рассеяния
обмоток связан с вычислением удельных проводимостей для
частей паза, занятых обмоткой, клином, и по головкам зуб-
цов [122].
Метод расчета магнитного поля (МП) проводника в пазу,
изложенный в разд. 1.4, позволяет на единой методической
основе определить суммарную индуктивность пазового рас-
сеяния.
Как уже отмечалось в гл. 2, комплексная потенциальная
функция для верхней полуплоскости
W t V t jU t
(3.33)
выражается через интеграл Шварца [165]:

176
W t U
t
d
1 1
1
2
. (3.34)
Рис. 3.4. К расчету индуктивности пазового рассеяния

177
Функция потока в точке
t a jb
, как видно из формулы
(3.34), имеет вид:
V t U
a
a b
d
1
1
2
2
2
. (3.35)
Потокосцепление элементарного контура с током
di
в
точке
t a jb
(рис. 3.4,б)
d V V
di
I
ab ab q
, (3.36)
где
V
ab
и
V
q
определяются по формуле (3.35), но
V
q
вычис-
ляется для точки
t q j
0
;
q
— координата точки на оси плоскости
t
, через кото-
рую проходит крайняя силовая линия, относящаяся к по-
току пазового рассеяния (линия
S—R—Q
на рис. 3.4,а).
Используя формулу (3.35) и график изменения скалярно-
го магнитного потенциала
U
на оси несложно найти:
V
I
q a
a q
q
2
1
23
2
23
2
ln , (3.37)
где
a
a a
23
2 3
2
.
Учитывая выражения для элементарного тока:
di dS dS
t t z z
,
где
t
;
z
— плотности тока соответственно в точке
t a jb
и ее образе,
z x jy
;
178
dS dadb
t
;
dS dxdy
z
— элементарные сечения в ука-
занных точках;
и формулу
dS dS dz dt
z t
2
,
можем получить два выражения для удельной проводимости
пазового рассеяния от потенциального магнитного поля
p
I
(
— полное потокосцепление с проводниками
паза потока вектора напряженности потенциального МП):
p
z
ab
S
t
q
S
V
dz
dt
dS V
t
1
2
1
2
, (3.38)
p
z
ab
S
z
q
S
V dS V
z
1
2
1
, (3.39)
где
S
z
— сечение проводника в плоскости
z
,
V V I
ab
ab
2 ;
V V I
q
q
2 .
Первое выражение связано с интегрированием по сечению
проводника в плоскости
t
, второе — в плоскости
z
.
Для удельной магнитной проводимости рассеяния про-
водника, обусловленной дополнительным полем
H
0
, напря-
женность которого линейно зависит от координаты
y
(рис.3.4,а), легко найти простую зависимость:
0
2 3
2
2
3
4
3
2 4
2
3
2 3 4
1
3 2
b h
h h
h h
h
h h h
. (3.40)
Эта удельная проводимость будет противоположна по знаку
удельной проводимости
p
вследствие встречного направле-
ния потенциального
H
p
и дополнительного
H
0
полей рас-
сеяния паза.

179
Для результирующей удельной магнитной проводимости
пазового рассеяния будет справедливо
p
0
.
По формулам (3.38), (3.40) рассчитывались удельные про-
водимости пазового рассеяния для немагнитной области
рис.3.4,а, имеющей:
b
1
5 ;
h
1
25 ;
b
2
3 ;
h
2
15 ;
b
2 ;
h
4
2 657 , ;
0 255 10
2
, м .
Было получено
p
0
2 55 0 686 1 864, , , .
Расчет по общепринятой методике, учитывающей рассеяние
по головкам соседних зубцов [122], дает результат: 2 253, .
Следует заметить, что величина рассчитываемой пазовой
индуктивности рассеяния, учитывающей магнитные потоки
не только в областях обмотки и клина, но также воздушного
зазора и второго зубчатого сердечника, будет функцией вза-
имного положения сердечников. Для практического приме-
нения целесообразно фиксировать либо только среднюю ве-
личину ее минимальных и максимальных значений, соответ-
ствующих положениям сердечников: паз — против паза и
паз — против зубца, либо дополнительно указать амплитуду
и фазу основной гармоники ее переменной составляющей.
Введение единого понятия пазовой индуктивности рассеяния
устраняет необходимость вычислять индуктивность рассея-
ния «по головкам зубцов».
Рассмотренный метод может найти применение для рас-
чета пазовой реактивности: короткозамкнутых обмоток асин-
хронных двигателей при малых скольжениях, когда поверх-
ностным эффектом вытеснения тока можно пренебречь; од-
нослойных и двухслойных (при совпадении по фазе токов в
слоях) обмоток крупных машин переменного тока; компен-
сационных обмоток машин постоянного тока и др.
Выводы.
1. На основе теории функций комплексного переменного
введено обобщенное понятие удельной магнитной проводи-
мости пазового рассеяния при произвольном взаимном по-
180
ложении сердечников статора и ротора, автоматически учи-
тывающее совокупность ее известных компонентов, в том
числе проводимость рассеяния по головкам зубцов.
2. Методика расчета обобщенной индуктивности пазового
рассеяния позволяет учесть изменения поля пазового рас-
сеяния при взаимном перемещении зубцовых структур про-
тиволежащих сердечников.
3.4. Индуктивные параметры обмоток, обусловленные
результирующим магнитным полем воздушного зазора с
локально учитываемой двухсторонней зубчатостью
Будем, для общности случая, рассматривать вентильную
машину (ВМ) явнополюсного типа с электромагнитным воз-
буждением, содержащую три обмотки возбуждения (одну не-
зависимого
fd
н и две последовательного возбуждения
fd fq
с c, , три фазы якоря (
A,B,C
) и демпферную обмотку
(ДО).
При заданных начальных значениях независимых токов
i
н
п1 н
т
i i i i i i i
A B fd D D Dr
1 2
... ,
где
i
п1
— ток звена постоянного тока преобразователя часто-
ты, протекающей через сглаживающий дроссель и после-
довательные обмотки возбуждения вентильной машины;
i
Dk
, (
k r
1 2, ,... ) — контурный ток
k
-го участка ДО, со-
стоящего из двух соседних стержней и перемычек между
ними,
и углового положения ротора
вычисляются по методике,
изложенной в разделе 2.2, магнитная индукция и коэффици-
енты насыщения магнитной цепи в 2
1 1
Q n z
счетных точ-
ках воздушного зазора (ВЗ)
k F F
, (3.41)
