Аракелян А.К., Афанасьев А.А. Вентильные электрические машины и регулируемый электропривод. Книга 1
Подождите немного. Документ загружается.

191
qx
p
x
b
p
max
2 2
cos
.
Для ярма якоря может быть найдена аппроксимирующая
функция, учитывающая неравномерность распределения ин-
дукции по длине ярмового участка:
F f B
a a
cp
, (3.63)
где
B B dx
x
cp
1
0
— (3.64)
среднее значение на полюсном делении индукции в воз-
душном зазоре.
Индукции в ярме и полюсном сердечнике индуктора на-
ходятся по формулам:
B
S
S
B
l
S
F F
B
S
S
B
l
S
F F
B
S
S
B
l
S
F F
a
a
f
a
f
m
m
f
m
f
m
m
f
m
f
и
и
cp
и
max cp
min cp
2
2
4
4
0 2
2
0 2
2
0 2
2
,
,
,
(3.65)
где
S
,
S
a
и
,
S
m
— площади сечений полюсного окна, ярма и
полюсного сердечника индуктора;
l
2
— длина полюсного сердечника индуктора;
F
f
— МДС обмотки возбуждения на один полюс;
F F F F
m m a
2
и
— магнитное напряжение индуктора,
равное сумме магнитных напряжений полюсного сердеч-
ника, стыка этого сердечника с ярмом индуктора и ярма
индуктора;

192
f
;
f
— удельные проводимости рассеяния соответст-
венно полюсного сердечника и полюсных наконечников.
Задаваясь рядом численных значений индукции
B
cp
и
используя аппроксимирующие зависимости для кривых на-
магничивания материалов сердечника и ярма индуктора,
можем решить нелинейную систему уравнений (3.65) при
F
f
const относительно магнитного напряжения
F
2
, то есть
получить табличную зависимость:
F f B
2 2
cp
. (3.66)
При расчете этой зависимости среднюю магнитную на-
пряженность полюсного сердечника находим из выражения:
H H H H
m m m m
1
6
4
max min cp
,
где
H
m
cp
соответствует индукции:
B B B
m m m
cp max min
1
2
.
Табличная зависимость (3.66) аппроксимируется сплай-
нами.
Суммарное магнитное напряжение для силовой линии,
проходящей через точку воздушного зазора с координатой
x
будет равно полному току, сцепленному с этой линией, —
сумме МДС обмоток:
U F
x x
м
, (3.67)
где
U F B F B F B F B
x x x zx x a
м cp cp
2
, (3.68)
F F F F F F
x fx dx qx dx qx
к к
, (3.69)
F
w
p
i
w
p
i
f x
f
f
f
f f x
н
н
c
c
П
2 2
, (3.70)
193
П
при
при
при
fx
p p
p
p
p
p
b x b
x
b
x b
x
b
b x
1 2 2
2
2 2
2
2 2
, ;
,
, ,
; (3.71)
F
wk
p
i
x
dx
w
d
3
1
cos , (3.72)
F
wk
p
i
x
qx
w
q
3
1
sin , (3.73)
F w i
x
dx d d
к к к
sign cos
, (3.74)
F w i
x
qx q q
к к к
sign sin
, (3.75)
индексы
f f d q kd kq
н с, , , , , относятся к обмоткам воз-
буждения (независимой и последовательной), якоря и ус-
покоительным, расположенным по осям
d
и
q
.
По уравнению (3.67) для каждой фиксированной точки
x x
k
при заданных токах обмоток находим значение ин-
дукции
B
x
, приняв предварительно за первое приближение:
B B
с x
x
р
0
.
При расчете поля в межполюсном пространстве определяем
в отдельности индукцию от продольной и поперечной со-
ставляющих МДС обмоток. Результирующее значение
194
B
x
b
x
p
2 2
находим методом наложения. При этом в
левой части уравнения (3.67) учитываем только магнитные
напряжения воздушного зазора и зубцового якоря.
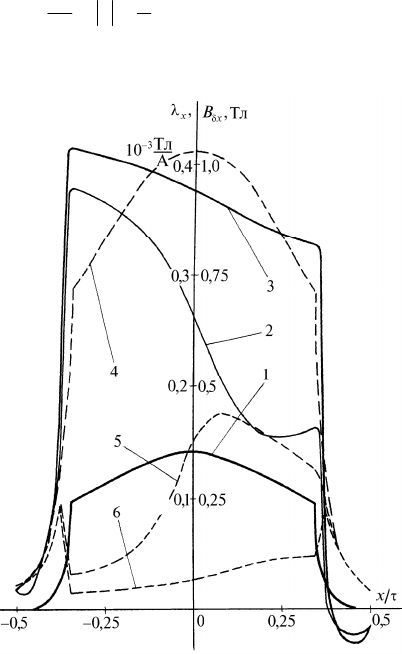
Рис. 3.5. Расчетные
кривые радиальной
со-ставляющей ин-
дукции в воздушном
зазоре (1,2,3) и сум-
марной удельной
дифференциальной
магнитной проводи-
мости (4, 5, 6) син-
хронного двигателя
СД102—8 (кривые
1,4 соответствуют
холостому ходу при
i i
f f
0 2,
ном
; 2,5 —
номинальному ре-
жиму; 3,6 — режиму
с номинальными
значениями тока
якоря по осям d и q
при i i
f f
2
ном
)
Кривые индукции в воздушном зазоре синхронного яв-
нополюсного двигателя СД102—8 мощностью 75 кВт с но-
минальной скоростью 750 об/мин, рассчитанные рассмот-
ренным выше методом для режимов нагрузки и идеального
холостого хода при различных значениях тока возбуждения,
приведены на рис. 3.5.
195
Разлагая кривую индукции
B
x
в тригонометрический
ряд Фурье, можем оценить ее гармонический состав. Опре-
делим потокосцепления обмотки якоря по осям
d
и
q
,
обусловленные основной гармоникой магнитного поля в воз-
душном зазоре:
d w x
l wk B
x
dx
1 1
2
2
4
cos , (3.76)
q w x
l wk B
x
dx
1 1
2
2
4
sin . (3.77)
Учитывая, что эти потокосцепления являются функцией
токов всех обмоток машины, можем найти динамические
индуктивности взаимоиндукции обмоток якоря с другими
обмотками в таком виде:
~
cos
L
i
l wk
B
i
x
dx
adr
d
r
w
x
r
1
1
2
2
4
, (3.78)
~
sin
L
i
l wk
B
i
x
dx
aqr
q
r
w
x
r
1
1
2
2
4
, (3.79)
где
B
i
F
i
x
r
x
x
r
, (3.80)
x
x
x
B
F
. (3.81)
196
Результирующую удельную дифференциальную магнитную
проводимость
x
для силовой линии с координатой
x
в воз-
душном зазоре находим численным методом, задаваясь фик-
сированным приращением МДС обмоток
F F F
x x x
для
дискретной точки
x x
k
и определяя соответствующие при-
ращения магнитной индукции
B B B
x x x
. Тогда
x
x
x
B
F
.
На рис. 3.5 приведены кривые
x
, полученные указан-
ным методом для тех же режимов синхронного двигателя,
что и соответствующие кривые индукции
B
x
.
Используя уравнения (3.69)—(3.73) и (3.78)—(3.81), будем
иметь в частности:
~ ~
L L
l wk
p
x
dx
add ad
w
x
12
2
1
2
2
2
2
cos , (3.82)
~ ~
L L
l wk
p
x
dx
aqq aq
w
x
12
2
1
2
2
2
2
sin
, (3.83)
~
L l wk
w
p
x
dx
adf w
f
x
4
2
1
2
2
cos , (3.84)
~
L l
wk
p
x
dx
adq
w
x
12
2
2
2
1
2
2
2
sin . (3.85)

197
Анализ подынтегрального выражения формулы (3.85) пока-
зывает, что динамическая индуктивность взаимоиндукции
между перпендикулярными обмотками будет отлична от нуля
лишь в том случае, когда кривая
x
не является четной от-
носительно начала координат. Это наблюдается при нагрузке
машины, вызывающей несимметричное насыщение магнит-
ной цепи из-за наличия поперечного магнитного поля (маг-
нитные проводимости набегающего и сбегающего краев по-
люса неодинаковы). При отсутствии насыщения и при сим-
метричном насыщении
~
L
adq
0 .
По аналогии с изложенным выше можем для сосредото-
ченной обмотки возбуждения найти ее потокосцепление и
динамическую индуктивность самоиндукции, обусловленные
магнитным потоком воздушного зазора
4
ff f x
w l B dx
2
2
, (3.86)
~
L
l
l
w
p
dx
ff
ff
f
f
x
2
2
2
2
. 3.87)
Целесообразно индуктивности (3.82)—(3.84), (3.87) выра-
зить через их ненасыщенные значения
L
ad
,
L
aq
,
L
adf
,
L
ff
,
вводя соответствующие коэффициенты насыщения магнит-
ной цепи:
~
L
L
k
ad
ad
d
;
~
L
L
k
aq
aq
q
;
~
L
L
k
adf
adf
df
;
~
L
L
k
ff
ff
f
,
где
4
Формула (3.86) записана в предположении, что силовые линии
магнитного поля воздушного зазора сцеплены со всеми витками
обмотки возбуждения.

198
L
l
k
wk
p
k
ad aq
w
ad aq
( ) ( )
6
2
0
1
2
min
, (3.88)
L
l
k
wk w
p
k
adf
w f
f
2
2
0
1
min
, (3.89)
L
l
k
w
p
k
ff
f
b
0
2
2
min
, (3.90)
k
x
dx
x
dx
k k
x
dx
d
x
x
ad
x
cos
cos cos
min
2
2
2
2
2
2
0
2
2
2
2
, (3.91)
k
x
dx
x
dx
k k
x
dx
q
x
x
aq
x
sin
sin sin
min
2
2
2
2
2
2
0
2
2
2
2
, (3.92)
k
x
dx
x
dx
k k
x
dx
df
x
x
f
x
cos
cos cos
min
2
2
2
2
0
2
2
2
, (3.93)
k
dx
dx
k k
dx
f
x
x
b
x
2
2
2
2
0
2
2
min
, (3.94)
199
x
х x
k
0
—
удельная магнитная проводимость по силовой линии с
координатой
x
при отсутствии насыщения магнитной це-
пи (удельная магнитная проводимость воздушного зазо-
ра), при расчете которой выделяем две области воздуш-
ного зазора:
1)
x b
p
2 ,
k k
x
;
2) 2 2
x b
p
,
k k
x
1
;
x dx
— для продольного и
x qx
— для поперечно-
го магнитных полей;
k
ad
;
k
aq
;
k
f
— коэффициенты формы полей обмоток
якоря и возбуждения, определяемые выражениями:
k
x
k k
dx
ad
x x
2
2
2
2
cos
min
,
k
x
k k
dx
aq
x x
2
2
2
2
sin
min
,
k
x
k k
dx
f
x x
2
2
2
cos
min
;
k
b
1 — коэффициент ослабления магнитного потока воз-
буждения из-за неравномерности воздушного зазора в
пределах полюсного деления:
k
dx
k k
b
x x
1
2
2
min
.
Оценивая формулы для коэффициентов насыщения
(3.91)—(3.94), следует отметить два очевидных факта:
1. Насыщение главной магнитной цепи примерно одина-
ково влияет на индуктивные параметры как по оси
d,
так и
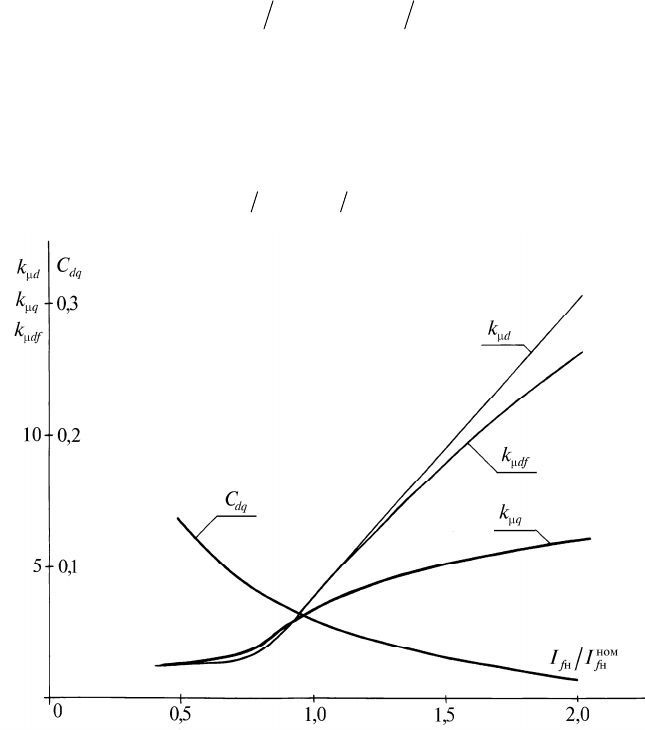
200
по оси
q
машины. Действительно, используя обобщенную
теорему о среднем [250], можем написать
k
d
I I
;
k
q
II II
,
где
I II
;
I II
— удельные магнитные проводимости, соот-
ветственно результирующая и воздушного зазора, взятые
в некоторых точках
x
I II
и
x
I II
полюсного де-
ления:
2 2
x
. (3.95)
Рис. 3.6. Зависимость коэффициентов насыщения от тока возбуж-
дения при номинальных значениях тока якоря по осям d и q
