Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

The metric, or, h ow to ra ise and lower indices 447

with T

···µ

···ν

def

= T



αα

, . . . ,αα

αα

, e

, . . . , e



Change of coordinates of a





-tensor

THEOREM 16.39 Let T = T

···µ

···ν

⊗···⊗e

⊗αα

αα

⊗···⊗αα

αα

be a





tensor. During a basis change B

′

= LB the coordinates T

···µ

···ν

are transformed

according to the rule

′

···µ

···ν

= Λ

···Λ

···L

···ρ

···σ

For this reason, a





-tensor is said to be p times covariant and q times

contravariant.

16.3

The metric, or:

how to raise and l ower indices

16.3.a Metric and pse udo-metric

DEFINITION 16.40 A metric (or scalar product) on a ﬁnite-dimensional real

vector space E (K = R) is a symmetric, positive deﬁnite bilinear form; in other

words it is a bilinear map

g : E

−→ R,

(u, v) 7−→ g(u, v),

such that g(u, v) = g(v, u) for a ny u, v ∈ E , and such that g(u, u) > 0 for any

nonzero vector u.

A pseudo-metric on a ﬁnite-dimensional real vector space E is a symmetric

deﬁnite b ilinear form (i.e., the only vector u for which we have g(u, v) = 0 for

all v ∈ E is the zero vector); however, g(u, u) itself may be of arbitrary sig n

(and even zero, for a s o-called light-like vector in special relativity).

Remark 16.41 A metric (resp. pseudo-metric ) g can be seen, wit h t h e isomorphisms described

in the previous sections, as a





-tensor.

DEFINITION 16.42 (Coefﬁcients g

µν

) Let g be a metric on a real vector space

E of dimension n. Let B = (e

, . . . , e

) be a basis of E and (αα

αα

, . . . ,αα

αα

) its

dual basis. The coordinates of g in the basis (αα

αα

⊗αα

αα

)

µν

of E

∗

⊗ E

∗

are

448 Tensors

Hermann Minkowski (1864—1909), German mathematician, was

born in Lithuania and spent his childhood in Russia. Since tsarist

laws prevented Jews from obtaining a dece nt education, his parents

emigrated to Germany. One of his brothers became a great physi-

cian, while he himself turned to mathematics. He taught in Bonn,

in Königsberg, and then at the Zürich polytechnic school, where

Albert Einstein was his student. His mathematical works concern

number theory and mathematic physics. He gave a geometric inter-

pretation of Einstein’s special relativity, which is the most natural

framework, and his formalism, generalizing the notion of scalar

product and distance in space-time is still used today.

denoted g

µν

. In other words, we have

g = g

µν

⊗dx

Since g is symmetric, it follows that g

µν

= g

νµ

for all µ, ν ∈ [[1, n]].

Example 16.43 The most important example of a metric is the euclidean metric which, in the

canonical basis (e

)

of E , is gi ven by coordinates

µν

1 if µ = ν,

0 if µ 6= ν.

DEFINITION 16.44 A basis B = (e

, . . . , e

) is orthonormal if

g(e

, e

) = δ

µν

for any µ, ν.

There can only be an orth onormal basis if the space is carrying a “true” metric,

and not a pseudo-metric (since the coordinates above describe the euclidean

metric in B).

DEFINITION 16.45 (Minkowski pseudo-metric) The Minkowski space is the

space R

with the pseudo-metric deﬁned by

µν

= η

µν

def







1 if µ = ν = 0,

−1 if µ = ν = 1, 2, or 3,

0 if µ 6= ν.

(16.3)

The space R

with this pseudo- metric is denote M

1,3

. This metric was int ro-

duced by H. Minkowski as the natural setting for the description of space-time

in einsteinian relativity.

DEFINITION 16.46 (Scalar product) The sca lar product of the vectors u and

v in E is the quantity

The metric 449

u ·v

def

= g(u, v).

If g is a pseudo-metric, we will a lso speak of pseudo-scalar product. It should

be noticed however that most books of relativity theory do not make an explicit

distinction; it is also customary to speak of minkowskia n scalar product, or

more simply of minkowskian product.

PROPOSITION 16.47 The coordinates of the metric g are given by the scalar products

(deﬁned by g) of the basis vectors

µν

= e

·e

Proof. Indeed, we have e

·e

= g(e

, e

) = g

ρσ

αα

⊗αα

αα

, e

)

= g

ρσ



αα

, e



〈αα

αα

, e

〉 = g

ρσ

= g

µν

16.3.b N atural duality by means of the metric

Once a basis in E is chosen, we can exhibit an isomorphism between E and

∗

, wh ich associates to a g iven basis vector e

the dual vector αα

αα

, and which,

therefore, associates to an arbitrary vector v = v

the linear form

ω =

αα

However, this isomorphism is not really interesting, because it depends on the

basis that has been chosen

(the terminology used is that the isomorphism is

noncanonical.)

Using the metric tensor g, it is possible to introduce a d uality of somewhat

different nature (a metric duality) between E and E

∗

which will be canonical

(i.e., it does not depend on the choice of a basis

Indeed, if u ∈ E is a vector, we can introduce a linear form

u ∈ E

∗

on E

using the bilinear form g: it is given by

u : E −→ R,

v 7−→ g(u, v) = u ·v

for any vector v. We denote this

u = g(u, ·).

DEFINITION 16.48 Let E be a real vector s pace with a metric g, a nd let B =

)

be a basis of E . The covariant coordinates of a vector u ∈ EE

EE are the

coordinates, in the basis (αα

αα

)

dual to B, of the linear form

u ∈ E

∗

deﬁned

by 〈

u, v〉 = u ·v for all v ∈ E .

This “artiﬁcal” aspect is visible even in the way it is expressed: one has to abandon the

Einstein c o nventions and explicitly write a summation sign in ω =

αα

, since the two

indices µ are “at the same level.” This is of course not a coincidence.

It depends on the metric, but the metric is usually given and is an intrinsic part of the

problem considered.

450 Tensors

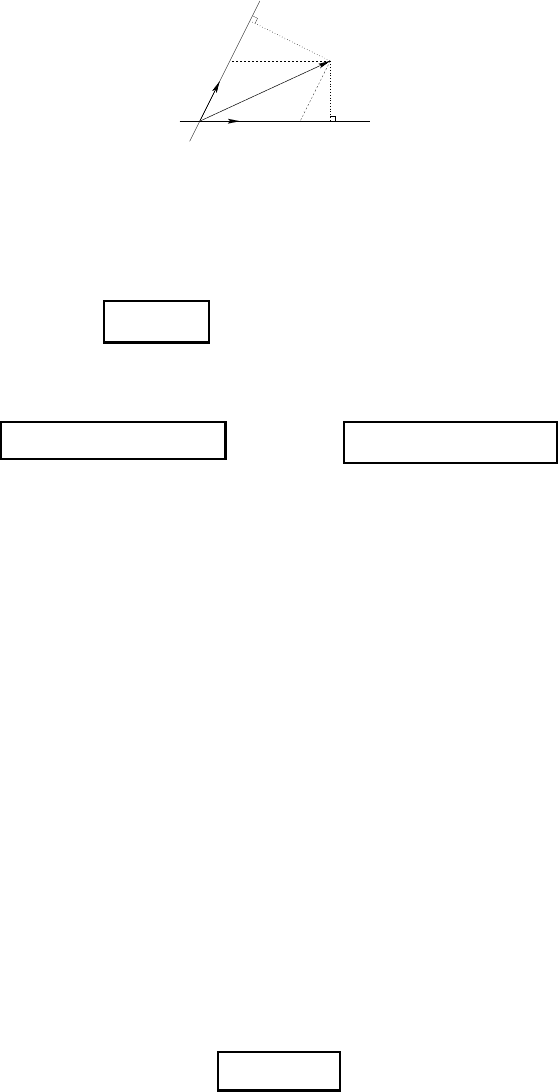
Fig. 16.1 — Contravariant and covariant coordinates of a vector of R

with the usual

euclidean scalar product. The vectors e

and e

have norm 1.

Those coordinates are denoted u

, so that we have

u = u

αα

whereas u = u

THEOREM 16.49 Let u ∈ E be a vector. Its contravariant and covariant coordi-

nates are given respectively by

= 〈αα

αα

, u〉 = 〈dx

, u〉 and u

= u ·e

= g(u, e

Proof. The ﬁrst equality is none other than the deﬁnition 16.1 of the contravariant

coordinates of a vector. To prove the second equality, remember that, by t he very

deﬁnition of

u, we have u ·e



u, e



and therefore

u ·e



αα

, e



= u



αα

, e



= u

It follows that the covariant and contravariant coordinates of a vector are

given by totally different means. Fix a vector u and choose a basis (e

)

. The

ν-th contravariant coordinate of u in (e

), u

= αα

αα

(u), is obtained using the

linear form αα

αα

, which depends not only on e

, but on all vectors of the basis

)

. On the other hand, the covariant coordinate u

is given by the scalar

product of u with e

, wh ich does not depend on the other basis vectors.

Remark 16.50 We see that the covariant coordinates correspond to orthogonal projections on the

axis spanned by the basis vector (requiring a metric to make precise the notion of orthogo-

nality), whereas contravariant coordinates correspond to projections on the axis parallel to all

others (and the metric is not necessary). See ﬁgure 16.1.

 Exercise 16.4 Show that, in an orthonormal basis, the covariant and contravariant coordi-

nates are identical.

16.3.c Gy mnas tics: raising and lowering ind ices

THEOREM 16.51 Let u ∈ E be a vector with contravariant coordinates u

and

covariant coordinates u

. Then we have

= g

µν

The metric 451

Proof. Indeed, we ﬁnd that u

= u ·e

= (u

) ·e

= u

·e

) = g

µν

Hence t he coefﬁcients (g

µν

)

µ,ν

turn out to be useful to lower an index.

This does not apply only to vectors, but may be done for tensors of arbitrary

type, always using the metric to transform a





-tensor into a



p−1

q+1



-tensor.

However, beware! When performing such manipulations, the order of the

indices must be carefully taken ca re of (see Remark 16.60).

THEOREM 16.52 Let ωω

ωω ∈ E

∗

be a linear form. There exists a unique vector

ωω

ωω ∈ E

such that

〈ωω

ωω, v〉 =

ωω

ωω ·v for all v ∈ E .

This result comes from the deﬁniteness of the metric and the fact that E

and E

∗∗

are isomorph ic in ﬁnite dimensions. Th e explicit construction of

ωω

is described in Proposition 16.54.

DEFINITION 16.53 The contravariant coordinates of the linear ωω

ωω are the

contravar iant coordinates of the vector

ωω

ωω. With a slight abuse of notation,

they are denoted ω

, so that we have

ωω

ωω = ω

PROPOSITION 16.54 Let ωω

ωω ∈ E

∗

be a linear form. The following relations hold

between its covariant and contravariant coordinates:

ωω

ωω, e

and ω

= 〈αα

αα

ωω

ωω〉. (1 6.4)

We have seen how the metric tensor can be used to lower the contravariant

index of a vector, thus obtaining its covariant coordinates. Similarly, it can be

used to lower t he contravariant index of a linear form:

THEOREM 16.55 Let ωω

ωω be a linear form. Its covar iant and contravariant coordi-

nates satisfy the relations

= g

µν

Proof. By deﬁnition,

ωω

ωω = ω

, and moreover for any vector v ∈ E , we have

〈ωω

ωω, v〉 =

ωω

ωω ·v. In particular, ω



ωω

ωω, e



ωω

ωω ·e

= ω

·e

= ω

νµ

, and this,

together with the relation g

µν

= g

νµ

, concludes t he proof.

We now pass to the question of raising indices.

DEFINITION 16.56 (Coefﬁcients g

µν

) Let g = g

µν

⊗ dx

be the metric

tensor. Its dual

g = g

µν

⊗e

is deﬁned by

g(ωω

ωω,σσ

σσ)

def

= g(

ωω

ωω,

σσ

σσ) =

ωω

ωω ·

σσ

σσ ∀ωω

ωω,σσ

σσ ∈ E

∗

452 Tensors

In particular, the coefﬁcients g

µν

satisfy g

µν

g(αα

αα

,αα

αα

) by Theorem 16.27.

Moreover, we have

g ∈ E ⊗E ; that is, the dual of the metric is a





-tensor.

The dual ﬁrst appears in the coordinates of the ba sis vectors of E and E

∗

which are given by the following proposition:

PROPOSITION 16.57 The c ovariant and contravariant coordinates of e

and αα

αα

— denoted [e

]

, with square brackets — are given by

]

= g

µσ

, [αα

αα

]

= g

µσ

]

= δ

, [αα

αα

]

= δ

Proof. The ﬁrst e quality comes directly from v

= v · e

applied to v = e

. The

second equality holds because (αα

αα

)

is the σ-th contravariant coordinate of the vector

αα

, and is therefore equal to



αα



αα

= g

µν

. The third equality is t rivial

since the σ-th coordinate of e



αα

, e



. Finally, the last equality follows from

(αα

αα

)



αα

, e



THEOREM 16.58 The matrices g

µν

and g

µν

are inverse to each other, that is, we

have

µν

νρ

= δ

and g

µν

νρ

= δ

Proof. First we prove the second formula. According to Proposition 16.57, we have

µν

= (αα

αα

)

, hence g

µν

νρ

= (αα

αα

)

νρ

= (αα

αα

)

by Theorem 16.55. Then the desired

conclusion follows from Proposition 16.57 again.

The ﬁrst equality is implied by the second.

From this we can see that the dual tensor

g = g

µν

⊗e

can be used to

raise indices:

THEOREM 16.59 Let u ∈ E be a vector and let ωω

ωω ∈ E

∗

be a linear form. Then

their covariant and contravariant coordinates satisfy the following relations:

= g

µν

and ω

= g

µν

Proof. This is clear from to the formulas related to lowering indices, since g

µν

and

µν

are inverse to each oth er.

Of course these results are also valid (with identical proofs!) for





tensors, which are transformed into



p+1

q−1



-tensors by

g (i.e., by g

µν

Remark 16.60 This is where the abuse of notation consisting in putting together all

covariant indices (and all contravariant indices) becomes dangerous. Indeed, consider,

for instance, a tensor with co ordinates

Operations on tensors 453

in expanded notation, and suppose now th at, to simplify notation, we denote the coordinates

simply

µρ

using the fact that E ⊗ E

∗

⊗E is canonically isomorphic to E

⊗2

⊗E

∗

Now, suppose we want to lower the index µ by contracting it with the metric tensor.

Should the result be denoted

µν

or T

νµ

Only the original “noncondensed” form c an give the answer. If the metric tensor is used, it is

important to be c areful to write all indices properly in th e correct position.

16.4

Operations on tensors

Theorem 16.59 may be generalized, noting that the tensors g and

g are

used to transform





-tensors into



p+1

q−1



-tensors or



p−1

q+1



-tensors, respectively.

For instance, suppose we have a tensor denoted T

µν

in physics. We may

lower the index ν using g

µν

, deﬁning

νρ

def

ντ

µτ

This is the viewpoint of “ index-manipulations.” What is the intrinsic mathe-

matical meaning behind this operation?

The tensor T, written

T = T

µν

⊗e

⊗αα

αα

is the obj ect which associates the real number

T(ωω

ωω,σσ

σσ, v) = T

µν

to a triple (ωω

ωω,σσ

σσ, v) ∈ E

∗

⊗ E

∗

⊗ E. As to the tensor “ w here one index is

lowered,” it corresponds intrinsically to

T = T

νρ

⊗αα

αα

⊗αα

αα

: (ωω

ωω, u, v) 7−→ T

νρ

To deﬁne

T, it sufﬁces simply to be able to pass from u to σσ

σσ. But this is

precisely the role of g, since from u ∈ E we may deﬁne a linear form

u ∈ E

∗

by the relation

u : E −→ R, (16.5)

w 7−→ g(u, w).

Then we can deﬁne

T as the “object” which

1. takes as input the triple (ωω

ωω, u, v),

454 Tensors

2. transforms it into (ωω

ωω,

u, v), where

u is deﬁned by the relation (16.5),

3. outputs the real number T(ωω

ωω,

u, v):

T : E

∗

⊗ E ⊗ E −→ R,

(ωω

ωω, u, v) 7−→ T(ωω

ωω,

u, v).

The same operation may be performed to “raise a n index.” This t ime, the

tensor

g is used in order to deﬁne a vector, starting with a linear form (still

because of the metric duality).

To summariz e:

THEOREM 16.61 (Raising and lowering indices) The metric tensors g and

g can

be used to transform a





-tensor into a



p+1

q−1



-tensor or a



p−1

q+1



-tensor, respectively.

There is another fundamental operation deﬁned on tensors, namely, the

contraction of indices. Once again, to start with a concrete example, consider

a tensor

T = T

µν

⊗e

⊗αα

αα

We will associate to this





-tensor a





-tensor, by deﬁning

def

= T

µν

Thus we have performed an index contraction. For instance, the trace of a

linear operator in a ﬁnite-dimensional vector space is given by the contraction

of its indices.

Intrinsically, we are looking for a new tensor

T = T

: ωω

ωω 7−→ T

Notice that, taking an a rbitrary basis (e

)

and its dual basis (αα

αα

)

, we have

T(ωω

ωω,αα

αα

, e

) = T

µν

[αα

αα

]

= T

µν

= T

µν

= T

µν

Hence it sufﬁces to deﬁne the tensor

T by

T : E

∗

−→ R,

ωω

ωω 7−→ T(ωω

ωω,αα

αα

, e

and then the relation

T = T

with T

= T

µν

holds indeed (indepen-

dently of the choice of a basis).

THEOREM 16.62 (Index contraction) There exists an operation of “index contrac-

tion” which, for any choice of one covariant and one contravariant coordinate, trans-

forms a





-tensor into a



p−1

q−1



-tensor. This operation does not require the use of the

metric, and is deﬁned independently of the choice of a basis.

Change of coordinates 455

16.5

Change of coordinates

One of the most natural question that a physicist may as k is “how does a

change of coordinates transform a quantity q?”

First, notice that a change of coordinates may be different things:

• a simple is ometry of th e ambient space (rotation, translation, symme-

try,...);

• a change of Galilean reference frame (which is t hen an isometry in

Minkowski space-t ime with its pseudo-metric);

• a more complex abstract transformation (going from cartesian to polar

coordinates, arbitrary coordinates in general relativity,...).

16.5.a Curvilinear coordin ates

Consider general coordinates (x, y, z) in R

, which we rather denote (x

, x

or even X = (x

, . . . , x

) in order to easily generalize to a space with n dimen-

sions. For instance, this may be euclidean coordinates in R

Suppose given a set of functions which deﬁne new coordinates, called

curvilinear coordinates:

U =







= u

, . . . , x

= u

, . . . , x

These functions deﬁne a C

change of coordinates if (a nd only if) t he map

Φ : R

−→ R

, . . . , x

) 7−→ (u

, . . . , u

)

is of C

-class (its partial derivatives exist and are continuous), it is injective

and its image is open, and if Φ

−1

is of C

-class on this open subset (this is

called a CC

-diffeomorphism in mathematics, but physicists simply speak of

coordinate change). Recall th e following result of differential calculus [75]:

Φ is a C

-diffeomorphism if and only if it is of C

-class and its jacobian is

nowhere zero. In other words, its differential dΦ is a bijective linear map at

every point.

How is a vector such as a velocity vector, for instance, transformed? Its

norm, expressed in kilometers per hour (hence, in terms of a ﬁrst set of

coordinates) is not the same expressed in miles per second (in a second set

of coordinates). H owever, the velocity is a physical quantity independent of

the manner in which it is meas ured. Therefore, the intrinsic physical quantity

must not be mistaken for its coordinates in a given system of measurement.

456 Tensors

Unfor tunately, physicists often use the same word for those two very different

concepts! Or, which amounts to th e same thing here, the y omit to state

whether active or passive transformations are involved.

In what follows, we consider passive transformations: the space is invariant,

as well as the quantities measured; on the other hand, the coordinate system

varies, and hence the coordinates of the quantities measured als o change.

16.5.b Basis vectors

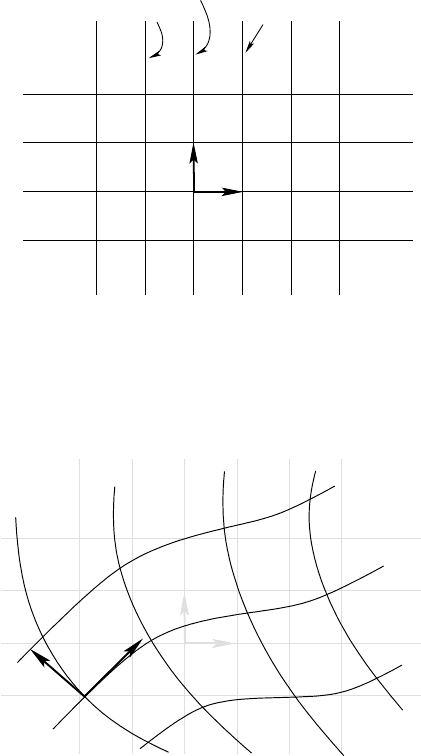
Let Y be a point in R, and let



(Y), . . ., e

(Y)



denote the basis vectors

in R

attached to t he point Y. This family does not depend on Y, since X

represents the canonical coordinates on R

Y e

= 0

= 1

= 2

= 3

= 1

= 2

= 3

We now want to ﬁnd the new vectors, at tached at the point Y

′

= Φ(Y) and tan-

gent to t he “coordinate lines,” which represent t he vectors



(Y), . . ., e

(Y)



after th e ch ange of coordinates. They w ill then be t he new b asis vectors. We

denote them



′

), . . . , e

′

)



Y e

′

= 1

= 2

= 4

= 3

= 0

= 1

= 2